【随想录6-1】环形链表相关问题及其证明_链表有环为什么一定会相遇 数学归纳法

试着解决如下问题

• 如何证明环形链表有环？
• 为什么双指针一定会在环内相遇？
• 如果快指针一次走三步是否一定相遇？5步呢？n步呢？
• 证明一下上一条
• 为什么此题快慢指针中，快指针比慢指针仅多走一步？为什么这么设置？
• 如何找到入环节点
• 证明一下上面方法的正确性

如何证明环形链表有环？

leetcode 141 题自己搜

为什么双指针一定会在环内相遇？

来自代码随想录群友穿靴子的猫的解释

假设快指针一次走x步，慢指针一次y步，相遇意味着二者路程差了n圈，一圈长度是C，则经过t时间，xt-yt=nC，n是快指针比慢指针多走的圈数，只要保证t=nC/(x-y)有整数解即可，令n=x-y，则必会相遇

为什么此题快慢指针中，快指针比慢指针仅多走一步？为什么这么设置？

源地址：https://stackoverflow.com/a/23662769

翻译翻译：

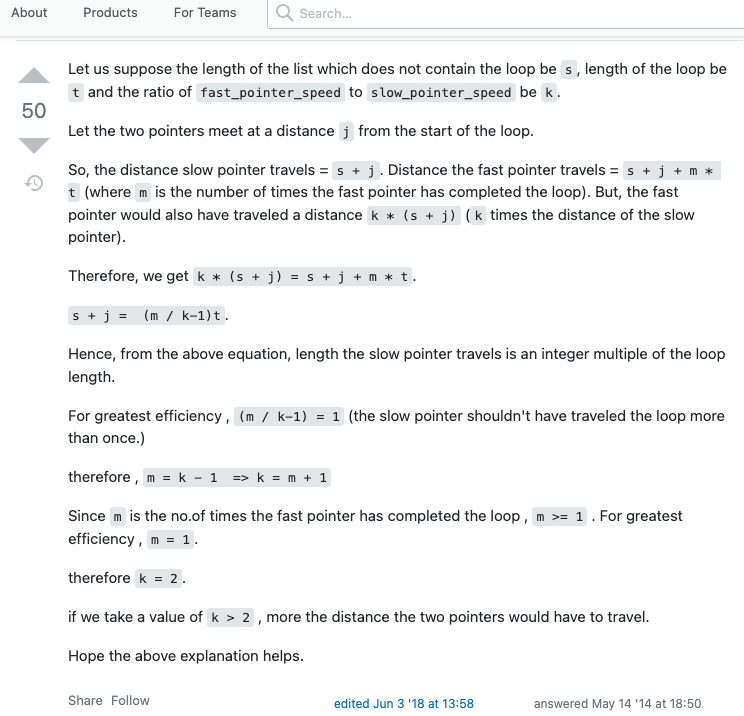
让我们假设不包含循环的列表的长度 be s，循环的长度 bet和fast_pointer_speed to slow_pointer_speed 的比率k。

（不包含环的节点长度为 s，环长度为t ，快慢指针速度比率为 k ）

让两个指针在距 j 循环起点一定距离处相遇。

因此，慢速指针移动的距离 = s + j。快速指针移动的距离 = s + j + m * t（其中m是快速指针完成循环的次数）。但是，快速指针也会移动一段距离 k * (s + j) （k为速度比率）。

因此，我们得到k * (s + j) = s + j + m * t。

s + j = (m / k-1)t.

因此，根据上面的等式，慢指针移动的长度是循环长度的整数倍。

为了获得最大的效率，(m / k-1) = 1（慢指针不应多次遍历循环。）

所以 ， m = k - 1 => k = m + 1

由于m是快速指针完成循环的次数，m >= 1。为了获得最大的效率，m = 1。

因此k = 2。

如果我们取值为k > 2，则两个指针必须移动的距离越大。

希望以上解释有帮助。

如果快指针一次走三步是否一定相遇？5步呢？n步呢？

链表是否有环 快指针走三步

简单证明一下上一条

可以看下本博客的第2个问题

假设快指针一次走x步，慢指针一次y步，相遇意味着二者路程差了n圈，一圈长度是C，则经过t时间，xt-yt=nC，n是的圈数，只要保证t=nC/(x-y)有整数解即可，令n=x-y，则必会相遇

这里涵盖了所有可能性，无论快慢指针速度比是多少，只要他俩都是整数速度，就一定能相遇

还可以看这个博客的第2部分的验证代码

【随想录6 】环形链表与回文链表总结(带正确性证明)

如何找到入环节点

代码随想录解释

证明一下上面方法的正确性

代码随想录解释

翻译翻译：

 					-------------------
                     |                 ^
                     v                 |
     0->1->2->3-> …… -> A ->....... -> B
     假设A为环入口，B为相遇点，设0到A距离为x,
     A到B距离为y,环的长度为c，
     快慢指针相遇是慢指针绕环n圈，快指针绕环m圈，
     由条件得快慢指针相遇时快指针走的长度是慢指针的2倍，则：
     2(x+nc+y)=x+mc+y；
     化简得x+y=(m-2n)c；
    
     这意味着从起点0相遇点B的长度为环长度的正整数倍；
     换句话说，就是现在让两个指针速度都变成1(重点！！！)，
     第一个指针从起点0出发，第二个指针从相遇点B出发，
     则两个指针最后一定会在B点相遇；
     但这是两个指针第一次相遇吗？
     不，因为两个指针速度是相同的，
     所以往前退一退，就会发现两个指针其实是在环的入口第一次相遇后，就一直重合了；
     所以代码就转换成两个速度为1的指针，一个从起点出发，一个从B点出发，第一次相遇的节点即为入环点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

源链接：https://stackoverflow.com/a/36214925