- 1Oracle又裁员!_oracle裁员
- 2KeeperErrorCode = ConnectionLoss 问题解决
- 37 Series FPGAs Integrated Block for PCI Express IP核基本模式配置详解
- 4If you want an embedded database (H2, HSQL or Derby), please put it on the classpath.
- 5python数组求和函数_python数据分析之Numpy数据库第三期数组的运算
- 6第三阶段应用层——1.7 数码相册—电子书(2)—编写通用的Makefile_在主目录下创建dianzi1和dianzi2两个文件夹,在dianzi1文件夹中创建file1 fi
- 7<网络安全>《70 微课堂<第11课 0day、1day、nday(精华版)>》_0day、1day、n day
- 8计算机领域顶级会议归纳(计算机视觉CV、机器学习ML、人工智能AI)_wacv
- 9RabbitMQ消费者Consumer实现_java rabbitmq consumer
- 10CKA 06_Kubernetes 工作负载与调度 Pod 管理 yaml 资源清单 标签 Pod 生命周期 容器探针_kubernetes工作负载 yaml
平衡二叉树java_平衡二叉树算法分析
赞
踩
1、平衡二叉树定义:
平衡二叉树(Balanced Binary Tree或Height-Balanced Tree)又称AVL树。它或者是一颗空树,或者是具有下列性质的二叉树:它的左子树和右子树都是平衡二叉树,且左子树和右子树的深度之差的绝对值不超过1。若将二叉树上结点的平衡因子bf(balance factor)定义为该结点的左子树的深度减去右子树的深度,则平衡二叉树上所有结点的平衡因子只可能为-1、0和1这三个值。
2、失去平衡情况分析:
假设结点A是一颗子平衡二叉树,当在以A为根结点的AVL树上插入一个新结点时,会出现以下三种情况:
1)如果插入前A—>bf=1(A的左子树深度比右子树深度多1),如果插入在A的左子树上且A的左子树深度增加了1,则此时A—>bf=2需要对树进行调整,如图2.1结点C为新插入的结点,C可以插入到B的左子树上(如图2.1(b))或者右子树上(如图2.1(c))。
2)如果插入前A—>bf=0(A的左子树和右子树深度相等),如果插入在A的左子树上且A的左子树深度增加了1,则此时只需要改变A的平衡因子为1即可不需要对树进行调整。如果插入在A的右子树上且A的右子树深度增加了1,则此时只需要改变A的平衡因子为-1即可不需要进行调整。
3)如果插入前A—>bf=-1(A的左子树深度比右子树深度少1),如果插入在A的右子树上且A的右子树深度增加了1,则此时A—>bf=-2需要对树进行调整,如图2.2结点C为新插入的结点,C可以插入在B的左子树上(如图2.2(b))或者右子树上(如图2.2(c))。
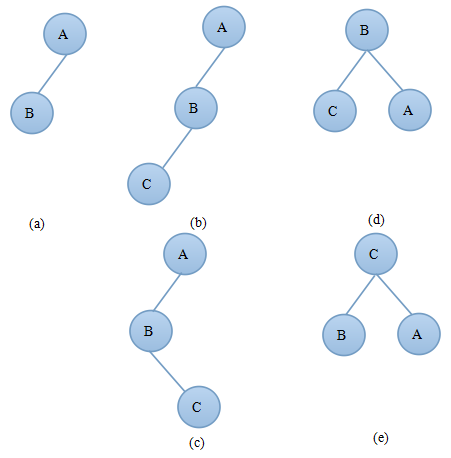
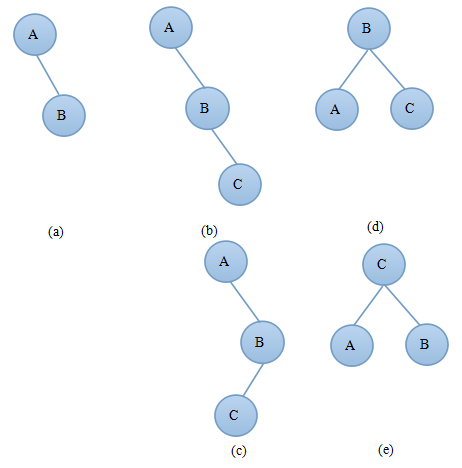
图2.1 图2.2
注意:上图中为了清楚的看到添加结点后失去平衡时的情况,省去了一些子结点,这些结点在下面的分析中会完整画出来
当出现图2.1(b)中的情况时只需要进行一次右旋转操作,旋转后得到如图2.1(d)所示的平衡二叉树。
当出现图2.1(c)中的情况时需要先对A的左子树B进行左旋操作,然后再进行右旋操作,旋转后得到如图2.1(e)所示的平衡二叉树。
当出现图2.2(b)中的情况时只需要进行一次右旋转操作,旋转后得到如图2.1(d)所示的平衡二叉树。
当出现图2.2(c)中的情况时需要先对A的右子树B进行右旋,然后再进行左旋操作,旋转后得到如图2.2(e)所示的平衡二叉树。
3.求旋转后各结点的平衡因子:
旋转后怎么确定各结点的新的平衡因子是平衡二叉树算法的关键点,我们需要按情况来一一推理。
一、当出现图2.1(b)(c)这两种情况时,需进行左平衡处理:
1)当新结点插入到B的左子树上时B—>bf=1,由此可知:deep(C)=deep(E)+1,deep(B)=deep(C)+1;由于插入新结点前A—>bf=1,deep(B)=deep(D)+1则插入新节点后deep(B)=deep(D)+2;图3.1.1为调整前的二叉树,图3.1.2为对A树进行右旋转后的AVL树:
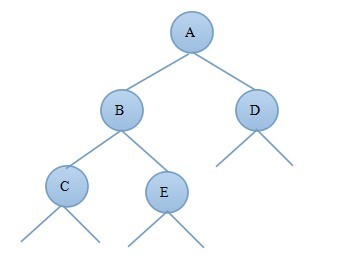
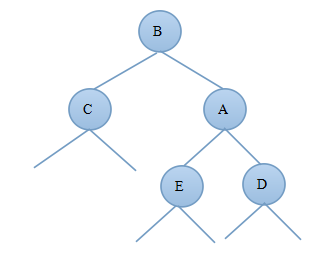
图3.1.1 图3.1.2
对比图3.1.1和3.1.2可知旋转后的新树中A的左子树发生了变化,B的右子树发生了变化,其他结点都没变;因此只需要重新算出A的平衡因子和B的平衡因子即可证明调整后的树是否为AVL树。
由上面的等式deep(B)=deep(D)+2,deep(B)=deep(C)+1,deep(C)=deep(E)+1
可以推出deep(E)=deep(C)-1=deep(B)-1-1=deep(D)+2-1-1=deep(D)可得出A—>bf=0
由调整后deep(E)=deep(D)可推出调整后deep(A)=deep(E)+1=deep(C)-1+1=deep(C)可得出B—>bf=0;
2)当新结点插入到B的右子树上时B—>bf=-1,由此可知:deep(C)=deep(E)-1,deep(B)=deep(E)+1;由于插入新结点前A—>bf=1,deep(B)=deep(D)+1则插入新节点后deep(B)=deep(D)+2;图3.2.1为调整前的二叉树,图3.2.2为先对B树进行左旋然后对A树进行右旋后的AVL树:
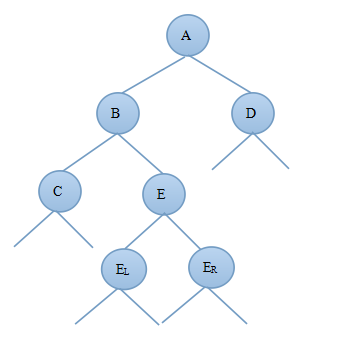

图3.2.1 图3.2.2
对比图3.2.1和3.2.2可知调整后的新树中A的左子树发生了变化,B的右子树发生了变化,E的左右子树都发生了变化,其他结点都没变,因此只需要重新算出A的平衡因子、B的平衡因子以及E的平衡因子即可证明调整后的树是否为AVL树。
此时由于调整后的B和A结点的平衡因子与E的左右子树EL和ER有关,因此需要根据E的平衡因子的不同来进行分析:
由上面的分析可得到deep(B)=deep(D)+2,deep(B)=deep(E)+1,deep(C)=deep(E)-1
1、当E—>bf=1时:deep(E)=deep(EL)+1,deep(ER)=deep(EL)-1
deep(C)=deep(E)-1=deep(EL)+1-1=deep(EL)可得B—>bf=0
deep(D)=deep(B)-2=deep(E)+1-2=deep(ER)+1+1+1-2=deep(ER)+1可得A—>bf=-1
由于deep(EL)=deep(ER)+1所以E—>bf=0
2、当E—>bf=0时:deep(E)=deep(EL)+1,deep(ER)=deep(EL)
deep(C)=deep(E)-1=deep(EL)+1-1=deep(EL)可得B—>bf=0
deep(D)=deep(B)-2=deep(E)+1-2=deep(ER)+1+1-2=deep(ER)可得A—>bf=0
由于B—>bf=0,A—>bf=0所以E—>bf=0
3、当E—>bf=-1时:deep(E)=deep(ER)+1,deep(ER)=deep(EL)+1
deep(C)=deep(E)-1=deep(EL)+1+1-1=deep(EL)+1可得B—>bf=1
deep(D)=deep(B)-2=deep(E)+1-2=deep(ER)+1+1-2=deep(ER)可得A—>bf=0
由于deep(EL)=deep(ER)-1所以E—>bf=0
二、当出现图2.2(b)(c)这两种情况时,需进行右平衡处理:
1)当新结点插入到C的左子树上时C—>bf=1,由此可知:deep(C)=deep(E)+1,deep(D)=deep(E)-1;由于插入新结点前A—>bf=-1,deep(B)=deep(C)-1则插入新节点后deep(B)=deep(C)-2;图3.3.1为调整前的二叉树,图3.3.2为先对C树进行右旋然后对A树进行左旋后的AVL树:
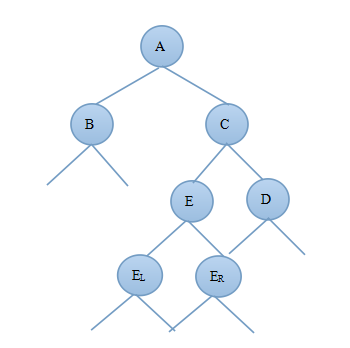
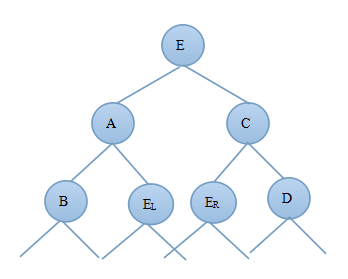
图3.3.1 图3.3.2
对比图3.3.1和3.3.2可知调整后的新树中A的右子树发生了变化,C的左子树发生了变化,E的左右子树都发生了变化,其他结点都没变,因此只需要重新算出A的平衡因子、B的平衡因子以及E的平衡因子即可证明调整后的树是否为AVL树。
此时由于调整后的A和C结点的平衡因子与E的左右子树EL和ER有关,因此需要根据E的平衡因子的不同来进行分析:
由上面的分析可得到deep(B)=deep(C)-2,deep(C)=deep(E)+1,deep(D)=deep(E)-1
1、当E—>bf=1时:deep(E)=deep(EL)+1,deep(ER)=deep(EL)-1
deep(B)=deep(C)-2=deep(EL)+1+1-2=deep(EL)可得A—>bf=0
deep(D)=deep(E)-1=deep(ER)+1+1-1=deep(ER)+1可得C—>bf=-1
由于deep(EL)=deep(ER)+1所以E—>bf=0
2、当E—>bf=0时:deep(E)=deep(EL)+1,deep(ER)=deep(EL)
deep(B)=deep(E)+1-2=deep(EL)+1+1-2=deep(EL)可得A—>bf=0
deep(D)=deep(E)-1=deep(ER)+1-1=deep(ER)可得C—>bf=0
由于A—>bf=0,C—>bf=0所以E—>bf=0
3、当E—>bf=-1时:deep(E)=deep(ER)+1,deep(ER)=deep(EL)+1
deep(B)=deep(C)-2=deep(E)+1-2=deep(EL)+1+1+1-2=deep(EL)+1可得A—>bf=1
deep(D)=deep(E)-1=deep(ER)+1-1=deep(ER)可得C—>bf=0
由于deep(EL)=deep(ER)-1所以E—>bf=0
2)当新结点插入到C的右子树上时C—>bf=-1,由此可知:deep(C)=deep(D)+1,deep(D)=deep(E)+1;由于插入新结点前A—>bf=-1,deep(B)=deep(C)-1则插入新节点后deep(B)=deep(C)-2;图3.4.1为调整前的二叉树,图3.4.2为进行左旋后的AVL树:
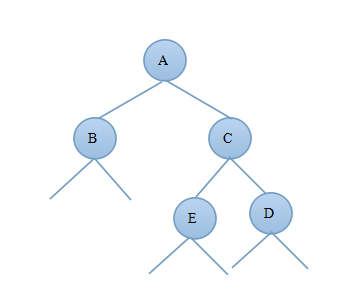
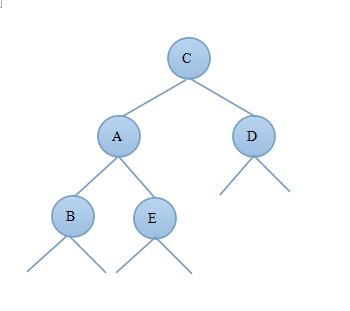
图3.4.1 图3.4.2
对比图3.4.1和3.4.2可知调整后的新树中A的右子树发生了变化,C的左子树发生了变化,其他结点都没变,因此只需要重新算出A的平衡因子和C的平衡因子即可证明调整后的树是否为AVL树。
由上面的等式deep(B)=deep(C)-2,deep(C)=deep(D)+1,deep(D)=deep(E)+1
可以推出deep(B)=deep(C)-2=deep(D)+1-2=deep(E)+1+1-2=deep(E)可得出A—>bf=0
由A—>bf=0调整后deep(A)=deep(E)+1=deep(D)-1+1=deep(D)可得出C—>bf=0;
4.Java实现代码:
1 packageorg.algorithms.tree;2
3 importjava.util.concurrent.ConcurrentLinkedQueue;4
5
6 public class BalanceBiTree{7
8 privateNode root;9
10 private intsize;11
12 public voidinsert(T t){13 if(root==null){14 root = newNode();15 root.bf = 0;16 root.data =t;17 size++;18 return;19 }20 addNode(root,t);21 }22
23 private booleanaddNode(Node nd,T t){24 boolean taller = false;25 Comparable cp = (Comparable)nd.data;26 int i =cp.compareTo(t);27 if(i==0){28 return false;29 }else if(i>0){30 if(nd.lChild==null){31 Node child = newNode();32 child.bf = 0;33 child.data =t;34 child.parent =nd;35 nd.lChild =child;36 size++;37 if(nd.bf==0){38 nd.bf = 1;39 return true;40 }41 nd.bf = 0;42 }else{43 taller =addNode(nd.lChild, t);44 if(taller){45 if(nd.bf==1){46 leftBalance(nd);47 taller = false;48 }else if(nd.bf==0){49 nd.bf = 1;50 taller = true;51 }else{52 nd.bf = 0;53 taller = false;54 }55 }56 }57 }else{58 if(nd.rChild==null){59 Node child = newNode();60 child.bf = 0;61 child.data =t;62 child.parent =nd;63 nd.rChild =child;64 size++;65 if(nd.bf==0){66 nd.bf = -1;67 return true;68 }69 nd.bf = 0;70 }else{71 taller =addNode(nd.rChild, t);72 if(taller){73 if(nd.bf==1){74 nd.bf = 0;75 taller = false;76 }else if(nd.bf==0){77 nd.bf = -1;78 taller = true;79 }else{80 rightBalance(nd);81 taller = false;82 }83 }84 }85 }86 returntaller;87 }88
89 public intgetSize(){90 returnsize;91 }92
93 private voidleftBalance(Node nd){94 Node leftChild =nd.lChild;95 if(leftChild.bf==1){96 nd.bf = 0;97 leftChild.bf = 0;98 rightRotate(nd);99 }else if(leftChild.bf==-1){100 Node rd =leftChild.rChild;101 switch(rd.bf) {102 case 1:103 leftChild.bf=0;nd.bf = -1;104 break;105 case 0:106 leftChild.bf=0;nd.bf = 0;107 break;108 case -1:109 leftChild.bf = 1;nd.bf = 0;110 break;111 }112 rd.bf = 0;113 leftRotate(leftChild);114 rightRotate(nd);115 }116 }117
118 private voidrightBalance(Node nd){119 Node rightChild =nd.rChild;120 if(rightChild.bf==1){121 Node ld =rightChild.lChild;122 switch(ld.bf) {123 case 1:124 rightChild.bf= -1; nd.bf = 0;125 break;126 case 0:127 rightChild.bf=0;nd.bf = 0;128 break;129 case -1:130 rightChild.bf = 0;nd.bf = 1;131 break;132 }133 ld.bf = 0;134 rightRotate(rightChild);135 leftRotate(nd);136 }else if(rightChild.bf==-1){137 nd.bf = 0;138 rightChild.bf = 0;139 leftRotate(nd);140 }141
142 }143
144 private voidleftRotate(Node nd){145 Node top =nd.rChild;146 nd.rChild =top.lChild;147 if(top.lChild!=null)148 top.lChild.parent =nd;149 top.lChild =nd;150 top.parent =nd.parent;151 if(nd.parent!=null){152 if(nd.parent.lChild ==nd)153 nd.parent.lChild =top;154 else
155 nd.parent.rChild =top;156 }else{157 root =top;158 }159 nd.parent =top;160 }161
162 private voidrightRotate(Node nd){163 Node top =nd.lChild;164 nd.lChild =top.rChild;165 if(top.rChild!=null)166 top.rChild.parent =nd;167 top.rChild =nd;168 top.parent =nd.parent;169 if(nd.parent!=null){170 if(nd.parent.lChild ==nd)171 nd.parent.lChild =top;172 else
173 nd.parent.rChild =top;174 }else{175 root =top;176 }177 nd.parent =top;178 }179
180 public voidprintTree(){181 ConcurrentLinkedQueue queue = new ConcurrentLinkedQueue();182 ConcurrentLinkedQueue tempQueue = new ConcurrentLinkedQueue();183 queue.add(root);184 int offset= 0;185 int counter=2;186 for(int i=0;i<50;i++)187 System.out.print(" ");188 while(queue.peek()!=null){189 Node node =queue.poll();190 String side = "L";191 if(node.parent!=null&&node.parent.rChild==node)192 side = "R";193 System.out.print(node.data+"("+(node.parent==null?"":node.parent.data)+" "+side+")");194 if(node.parent!=null&&node.parent.rChild!=node)195 for(int i=0;i
204 copyQueue(tempQueue,queue);205 System.out.println();206 for(int i=0;i<50-offset;i++)207 System.out.print(" ");208 }209 }210
211 }212
213 private void copyQueue(ConcurrentLinkedQueuesource,214 ConcurrentLinkedQueuetarget){215 while(source.peek()!=null){216 target.add(source.poll());217 }218 }219
220 private classNode{221
222 publicT data;223
224 publicNode lChild;225
226 publicNode rChild;227
228 publicNode parent;229
230 public intbf;231 }232 }


