机器学习-9.逻辑回归_根据提示,在右侧编辑器补充 python 代码,实现sigmoid函数。底层代码会调用您实现

EduCoder：机器学习—逻辑回归

第1关：逻辑回归核心思想

编程要求：

根据提示，在右侧编辑器补充 Python 代码，实现sigmoid函数。底层代码会调用您实现的sigmoid函数来进行测试。(提示: numpy.exp()函数可以实现 e 的幂运算)

测试说明:

测试用例：

输入：

1

预期输出：

0.73105857863

输入：

-2

预期输出：

0.119202922022

代码如下：

#encoding=utf8
#encoding=utf8
import numpy as np

def sigmoid(t):
    '''
    完成sigmoid函数计算
    :param t: 负无穷到正无穷的实数
    :return: 转换后的概率值
    :可以考虑使用np.exp()函数
    '''
    #********** Begin **********#
    return  1.0/(1+np.exp(-t))
    #********** End **********#

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

第2关：逻辑回归的损失函数

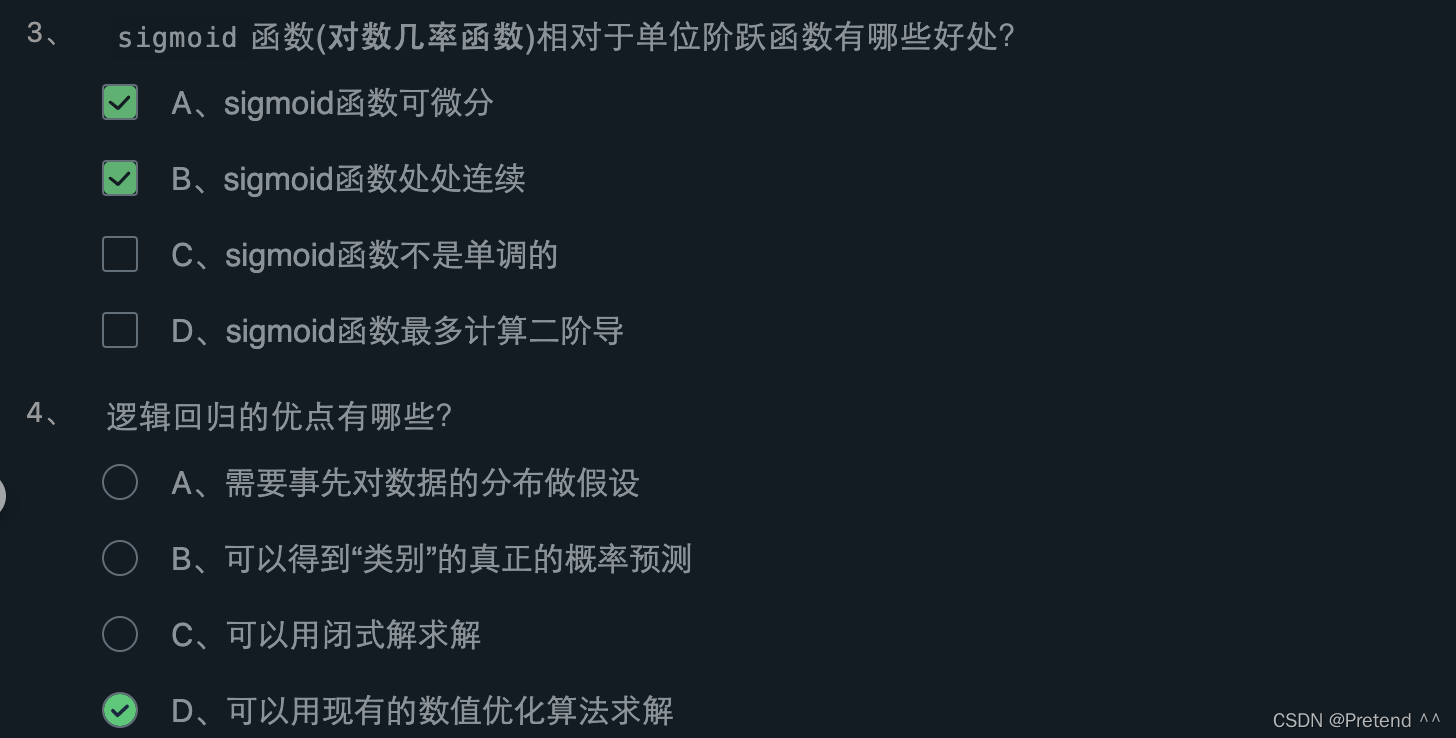
第3关：梯度下降

编程要求：

根据提示，使用 Python 实现梯度下降算法，并损失函数最小值时对应的参数theta，theta会返回给外部代码，由外部代码来判断theta是否正确。

测试说明：

损失函数为：loss=2∗(θ−3)
最优参数为：3.0
你的答案跟最优参数的误差低于0.0001才能通关。

代码如下：

## -*- coding: utf-8 -*-
import numpy as np
import warnings
warnings.filterwarnings("ignore")
def gradient_descent(initial_theta,eta=0.05,n_iters=1000,epslion=1e-8):
    '''
    梯度下降
    :param initial_theta: 参数初始值，类型为float
    :param eta: 学习率，类型为float
    :param n_iters: 训练轮数，类型为int
    :param epslion: 容忍误差范围，类型为float
    :return: 训练后得到的参数
    '''
    #   请在此添加实现代码   #
    #********** Begin *********#
    theta = initial_theta
    i_iter = 0
    while i_iter < n_iters:
        gradient = 2*(theta-3)
        last_theta = theta
        theta = theta - eta*gradient
        if(abs(theta-last_theta)<epslion):
            break
        i_iter +=1
    return theta
    #********** End **********#
    

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

第4关：动手实现逻辑回归 - 癌细胞精准识别

编程要求：

根据提示，在右侧编辑器Begin-End处补充 Python 代码，构建一个逻辑回归模型，并对其进行训练，最后将得到的逻辑回归模型对癌细胞进行识别。

测试说明：

只需返回预测结果即可，程序内部会检测您的代码，预测正确率高于 95% 视为过关。

提示：构建模型时 x 0是添加在数据的左边，请根据提示构建模型,且返回theta形状为(n,)，n为特征个数。

代码如下：

# -*- coding: utf-8 -*-
import numpy as np
import warnings
warnings.filterwarnings("ignore")

def sigmoid(x):
    '''
    sigmoid函数
    :param x: 转换前的输入
    :return: 转换后的概率
    '''
    return 1/(1+np.exp(-x))


def fit(x,y,eta=1e-3,n_iters=10000):
    '''
    训练逻辑回归模型
    :param x: 训练集特征数据，类型为ndarray
    :param y: 训练集标签，类型为ndarray
    :param eta: 学习率，类型为float
    :param n_iters: 训练轮数，类型为int
    :return: 模型参数，类型为ndarray
    '''
    #   请在此添加实现代码   #
    #********** Begin *********#
    theta = np.zeros(x.shape[1])
    i_iter = 0
    while i_iter < n_iters:
        gradient = (sigmoid(x.dot(theta))-y).dot(x)
        theta = theta -eta*gradient
        i_iter += 1
    return theta
    #********** End **********#


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

第5关：手写数字识别

编程要求：

填写digit_predict(train_sample, train_label, test_sample)函数完成手写数字识别任务，其中：

• train_image：训练集图像，类型为ndarray，shape=[-1, 8, 8]；

• train_label：训练集标签，类型为ndarray；

• test_image：测试集图像，类型为ndarray。

测试说明：

只需返回预测结果即可，程序内部会检测您的代码，预测正确率高于 0.97 视为过关。

代码如下：

from sklearn.linear_model import LogisticRegression

def digit_predict(train_image, train_label, test_image):
    '''
    实现功能：训练模型并输出预测结果
    :param train_sample: 包含多条训练样本的样本集，类型为ndarray,shape为[-1, 8, 8]
    :param train_label: 包含多条训练样本标签的标签集，类型为ndarray
    :param test_sample: 包含多条测试样本的测试集，类型为ndarry
    :return: test_sample对应的预测标签
    '''

    #************* Begin ************#
    # 训练集变形
    flat_train_image = train_image.reshape((-1, 64))
    # 训练集标准化
    train_min = flat_train_image.min()
    train_max = flat_train_image.max()
    flat_train_image = (flat_train_image-train_min)/(train_max-train_min)
    # 测试集变形
    flat_test_image = test_image.reshape((-1, 64))
    # 测试集标准化
    test_min = flat_test_image.min()
    test_max = flat_test_image.max()
    flat_test_image = (flat_test_image - test_min) / (test_max - test_min)

    # 训练--预测
    rf = LogisticRegression(C=4.0)
    rf.fit(flat_train_image, train_label)
    return rf.predict(flat_test_image)
    #************* End **************#


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33