神经网络---第一章 基础知识 1.0 人工智能与神经网络_人工智能1.0

0、背景

一个对中文一窍不通，只说英语的人关在一个封闭房间中。房间里有一本用英文写成的手册，指示该如何处理收到的汉语信息及如何以汉语相应地回复。房外的人向房间内递进用中文写成的问题。房内的人便按照手册的说明，查找到合适的指示，将相应的中文字符组合成对问题的解答，并将答案递出。

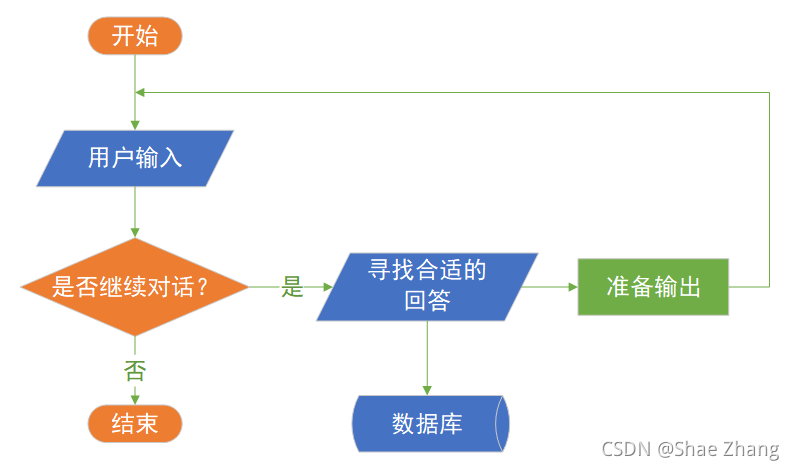
房间外面的人看到自己递进去的中文输入能得到回答，很可能就会认为房间内的人有智能，懂中文，就像现在的聊天机器人那样，那么这是“智能”么？读者们如果写过一些程序，就会想，我也可以写一个程序，根据一些规则和已有的数据，和用户进行某种程度的智能对话，那么AI和我的程序有区别么？

1、人工智能

(1)基本定义

a.智能地把某件特定的事情做好，在某个领域增强人类的智慧，这种方式又叫做智能增强

像搜索引擎，自动语言翻译，某个领域的智能助手那样的程序，帮助人类完成某种特定任务。这也叫做“弱人工智能”，或者“狭义人工智能”。

b.像人类一样能认知，思考，判断：模拟人类的智能

像人类一样能认知，思考，判断的智能软件。这是人工智能学科一开始就有的梦想。这样的智能也叫做“通用人工智能”（Artificial General Intelligence， AGI）， 或“强人工智能”。对于这样的人工智能，科幻小说有很多描写，也有一些研究，但是在实际的应用还没有什么突破。有学者认为，AGI是不可能通过目前人们编程程序的方式实现的 。尽管如此，社会上还是有人担忧有一天电脑的AGI会超过人类的智能，人类再也赶不上电脑，从而永远受制于电脑。

(2) 第二个层面，从技术的特点来看

如果一个程序解决任务（T）的效能（用P表示）随着经验（E）得到了提高，那么，这个程序就能从经验（E）中学到了关于任务（T）的知识，并让衡量值（P）得到提高。

a. 选择一个模型结构（例如逻辑回归，决策树等），这就是上面说的程序。

b. 用训练数据（输入和输出）输入模型。这就是上面的经验（E）。

c. 通过不断执行任务（T）并衡量结果（P），让P不断提高，直到达到一个满意的值。

机器学习的各种方法是如何从经验中学习呢？

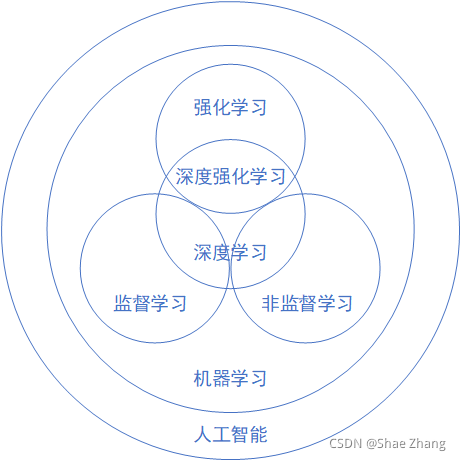
• 监督学习（Supervised Learning）
  通过标注的数据来学习，例如，程序通过学习标注了正确答案的手写数字的图像数据，它就能认识其他的手写数字。

• 无监督学习（Unsupervised Learning）
  通过没有标注的数据来学习。这种算法可以发现数据中自然形成的共同特性（聚类），可以用来发现不同数据之间的联系，例如，买了商品A的顾客往往也购买了商品B。

• 强化学习（Reinforcement Learning）
  我们可以让程序选择和它的环境互动（例如玩一个游戏），环境给程序的反馈是一些“奖励”（例如游戏中获得高分），程序要学习到一个模型，能在这种环境中得到高的分数，不仅是当前局面要得到高分，而且最终的结果也要是高分才行。

综合来看，如果我们把机器学习当作一个小孩，那么，教育小孩的方式就有根据正确答案指导学习（监督学习）；根据小孩实践的过程给予各种鼓励（强化学习）；还有自由探索世界，让小孩自己总结规律（无监督学习）。

(3) 第三个层面，从应用的角度来看，我们看到狭义人工智能在各个领域都取得了很大的成果。

• 翻译领域（微软的中英翻译超过人类）
• 阅读理解（SQuAD 比赛）
• 下围棋（2016）德州扑克（2019）麻将（2019）
  
  
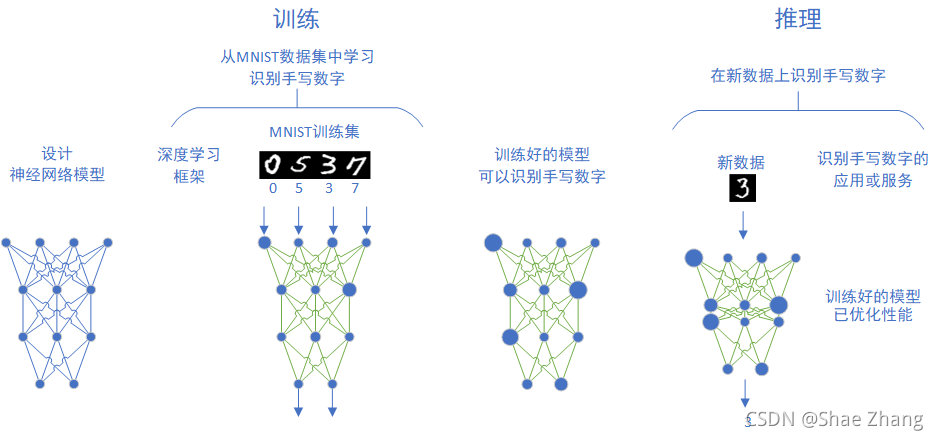
  首先我们要设计一个模型，然后用已经标注过的数据来训练这个模型，在训练过程中，模型的各个参数在多次训练中不断得到调整，最后得到了一个达到要求的模型。这个模型会被用于一个推理模型中，和其它程序模块一起组成一个应用程序或者是服务，能处理新的数据，满足用户的需求。

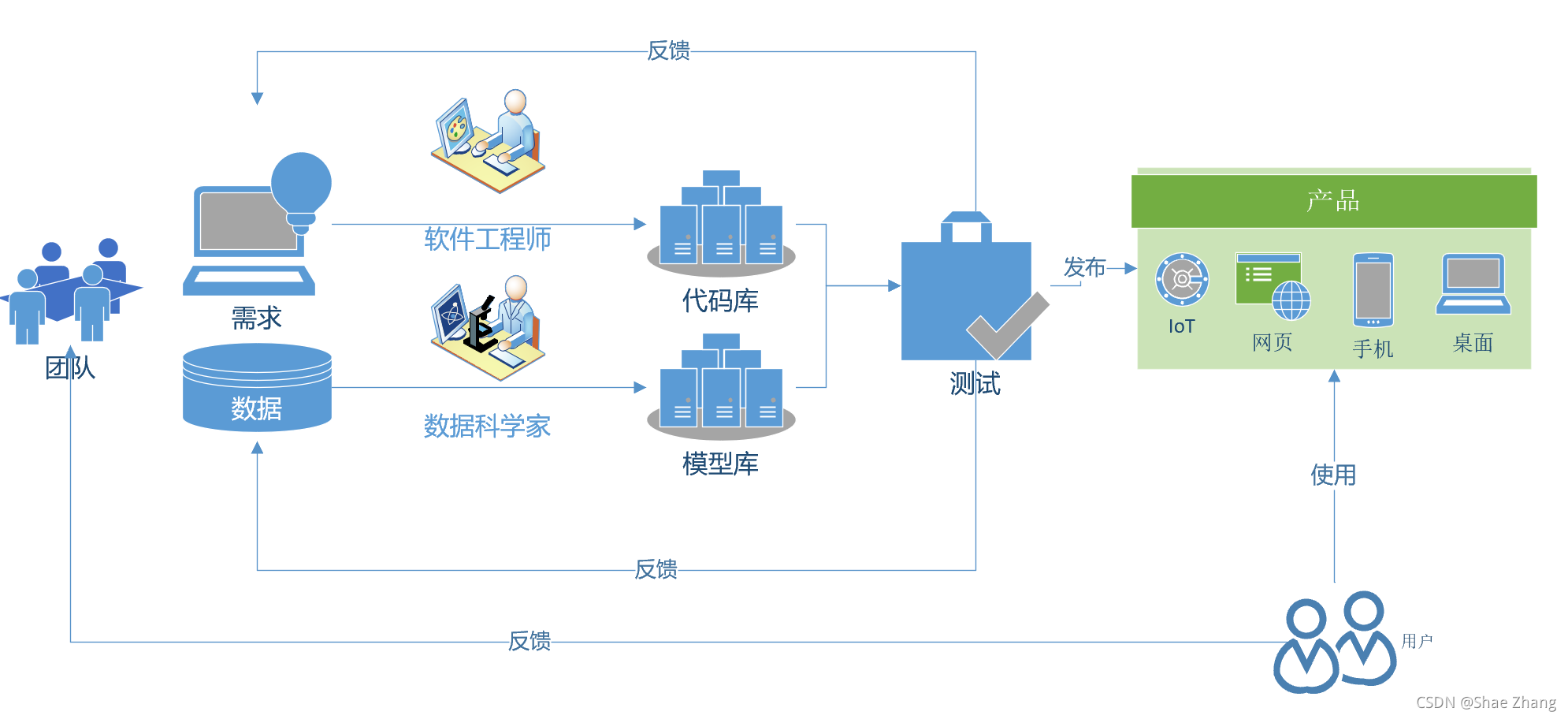
在现代软件开发流程中，程序的开发，和AI模型的开发的生命周期应该如何协作呢？软件工程师和数据科学家并肩工作，一个完善代码库，另一个完善模型库，最后的产品通过各种途径（网页/桌面程序/手机/IoT设备）交到用户手中

2、范式的演化

从Jim Gray的著作可以看到，现在谈论的AI大潮就是属于data exploration这个范式转换(颠覆性的改变)的一部分。

（1）范式演化的四个阶段

第一个阶段：经验

从几千年前到几百年前，人们描述自然现象，归纳总结一些规律。

人类最早的科学研究，主要以记录和描述自然现象为特征，不妨称之为称为“经验归纳”（第一范式）。人们看到自然现象，凭着自己的体验总结一些规律，并把规律推广到其他领域。这些规律通常是定性的，不是定量的。

第二个阶段：理论

这一阶段，科学家们开始明确定义，速度是什么，质量是什么，化学元素是什么（不再是五行和燃素）……也开始构建各种模型，在模型中尽量撇除次要和无关因素，例如我们在中学的物理实验中，要假设“斜面足够光滑，无摩擦力”，“空气阻力可以忽略不计”，等等。

第三个阶段：计算仿真

从二十世纪中期开始，利用电子计算机对科学实验进行模拟仿真的模式得到迅速普及，人们可以对复杂现象通过模拟仿真，推演更复杂的现象，典型案例如模拟核试验、天气预报等。这样计算机仿真越来越多地取代实验，逐渐成为科研的常规方法。科学家先定义问题，确认假设，再利用数据进行分析和验证。

第四个阶段：数据探索

在这个阶段，科学家收集数据，分析数据，探索新的规律。在深度学习的浪潮中出现的许多结果就是基于海量数据学习得来的。有些数据并不是从现实世界中收集而来，而是由计算机程序自己生成，例如，在AlphaGo算法训练的过程中，它和自己对弈了数百万局，这个数量大大超过了所有记录下来的职业选手棋谱的数量。

（2）范式各阶段应用

顾客参加一个抽奖活动，三个关闭的门后面只有一个有奖品，顾客选择一个门之后，主持人会打开一个没有奖品的门，并给顾客一次改变选择的机会。此时，改选另外一个门会得到更大的获奖几率么？

a.经验归纳

我们生活中的确碰到过各种抽奖时刻，有时候我们看似有很多赚大钱的机会，但是往往赢家不是自己。从这些生活经验出发，我们的直觉告诉我们要怎么选择呢？（我们做了调查，同学们的“基于生活经验的直觉”是这样分布的：X：Y）很多人会是从生活经验出发，感觉自己会中计，因此决定“我换了就上当了，我不换”，“我改变选择对运气不好，我不换”。当然，我们还可以用类比推理的办法，如果是100扇门，只有一扇门后面有奖品，我选中了一扇门，裁判打开了另外98个没有奖品的门，这个时候，我要换门么？

b.理论推导

本书的读者大多学过基本的概率知识，我们可以用概率的基本方法来解这一道题目。

---

设$A$为第一次选到了中奖门的概率，$B$为改变选择后选到了中奖门的概率，$C$为未改变选择后选到了中奖门的概率。

$P(A)=\frac{1}{3}$ （初始选择就是获奖门的获奖概率是$\frac{1}{3}$）

$P(A^{\prime })=\frac{2}{3}$ （当选中一个门之后， 其它两个门的获奖概率是$\frac{2}{3}$）

$P(B|A)=0$ （用户先选择了一个门，奖品在这个门后，用户后来改变选择，他的获奖概率是 0）

$P(C|A)=1$（用户选择了一个门，奖品在门后，后来他不改变选择，他的获奖概率是 1）

$P(B|A^{\prime })=1$，$P(C|A^{\prime })=0$（类似地， 用户首次选择的门后面没有奖品，他改变选择后，获奖概率是 1， 不改变选择，那么获奖概率是 0）

$P(B)=P(B|A)\times P(A)+P(B|A^{\prime })\times P(A^{\prime })=\frac{2}{3}$（所以，改变选择后中奖的概率，等于$\frac{2}{3}$）

$P(C)=P(C|A^{\prime })\times P(A^{\prime })+P(C|A)\times P(A)=\frac{1}{3}$（不改变选择而中奖的概率，等于$\frac{1}{3}$，和A 一样）

结论：$P(B)>P(C)$

---

c.数据模拟

我们还可以用数据模拟的方法，来看看在各种情况下，换或者不换的结果如何。
看我们的Python程序示例。

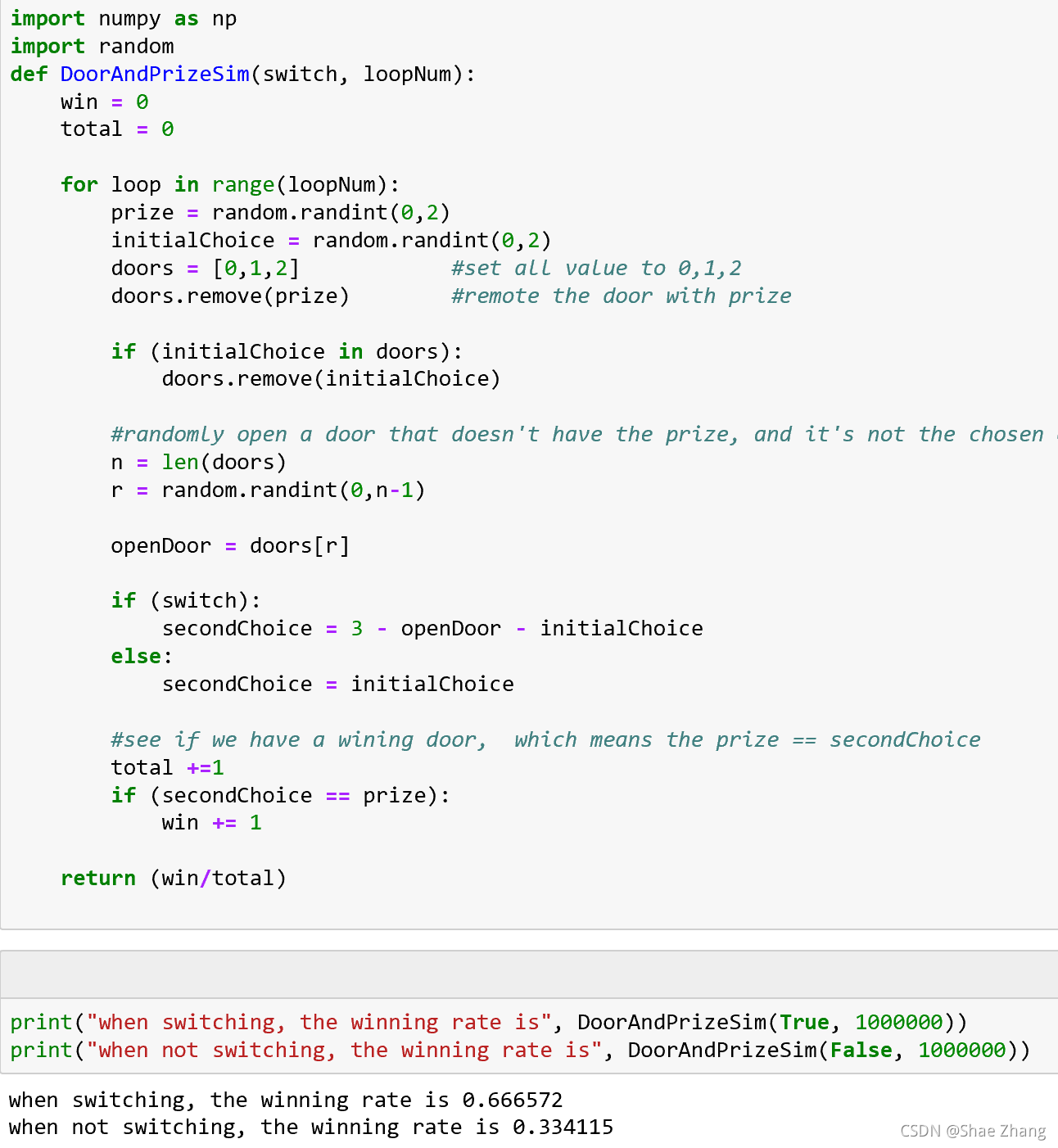
我们看到，当我们随机模拟一百万轮换门（switching）和不换门（not switching）的情况后，我们得到了这样的结果：

• 换门：最后得奖的概率是0.666572（约$\frac{2}{3}$）
• 不换门：最后得奖的概率是 0.334115（约$\frac{1}{3}$）

d.数据探索

当人类探索客观世界的时候，大部分情况下，我们是不了解新环境的运行规则的。这个时候，我们可以观察自己的行动和客观世界的反馈，判断得失，再总结出规律。这种学习方法，叫强化学习（Reinforcement Learning），可以使用这种方法来找出适合的策略。

3、神经网络的基本工作原理简介

（1）神经元细胞的数学模型

神经网络由基本的神经元组成，上图就是一个神经元的数学/计算模型，便于我们用程序来实现。

输入 input

(x1,x2,x3) 是外界输入信号，一般是一个训练数据样本的多个属性，比如，我们要预测一套房子的价格，那么在房屋价格数据样本中，x1可能代表了面积，x2可能代表地理位置，x3可能朝向。另外一个例子是，假设(x1,x2,x3)分别代表了(红,绿,蓝)三种颜色，而此神经元用于识别输入的信号是暖色还是冷色。

权重 weights

(w1,w2,w3) 是每个输入信号的权重值，以上面的 (x1,x2,x3) 的例子来说，x1的权重可能是0.92，x2的权重可能是0.2，x3的权重可能是0.03。当然权重值相加之后可以不是1。

偏移 bias

还有个b是怎么来的？一般的书或者博客上会告诉你那是因为$y=wx+b$，b是偏移值，使得直线能够沿Y轴上下移动。这是用结果来解释原因，并非b存在的真实原因。从生物学上解释，在脑神经细胞中，一定是输入信号的电平/电流大于某个临界值时，神经元细胞才会处于兴奋状态，这个b实际就是那个临界值。亦即当：

$$w_1\cdot x_1+w_2\cdot x_2+w_3\cdot x_3>=t$$

时，该神经元细胞才会兴奋。我们把t挪到等式左侧来，变成$(-t)$，然后把它写成b，变成了：

$$w_1\cdot x_1+w_2\cdot x_2+w_3\cdot x_3+b>=0$$

于是b诞生了！

求和计算 sum

Z = w 1 ⋅ x 1 + w 2 ⋅ x 2 + w 3 ⋅ x 3 + b = ∑ i = 1 m ( w i ⋅ x i ) + b

$$\begin{aligned} Z &= w_1 \cdot x_1 + w_2 \cdot x_2 + w_3 \cdot x_3 + b \\ &= \sum_{i=1}^m(w_i \cdot x_i) + b \end{aligned}$$ Z​=w1​⋅x1​+w2​⋅x2​+w3​⋅x3​+b=i=1∑m​(wi​⋅xi​)+b​

在上面的例子中m=3。我们把$w_i\cdot x_i$变成矩阵运算的话，就变成了：

$$Z=W\cdot X+b$$

激活函数 activation

求和之后，神经细胞已经处于兴奋状态了，已经决定要向下一个神经元传递信号了，但是要传递多强烈的信号，要由激活函数来确定：

$$A=\sigma (Z)$$

如果激活函数是一个阶跃信号的话，会像继电器开合一样咔咔的开启和闭合，在生物体中是不可能有这种装置的，而是一个渐渐变化的过程。所以一般激活函数都是有一个渐变的过程，也就是说是个曲线，如下图所示。

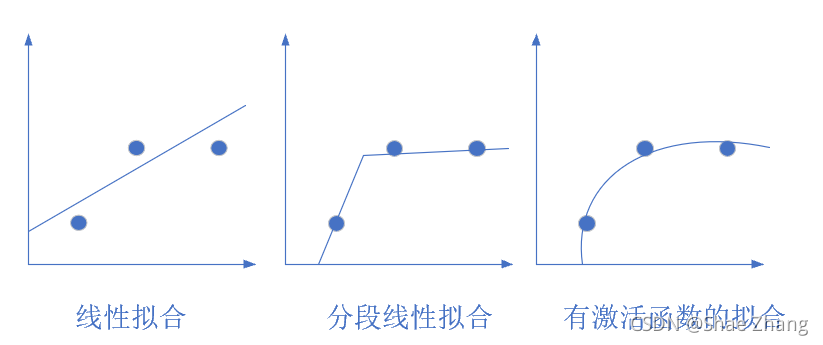
至此，一个神经元的工作过程就在电光火石般的一瞬间结束了。

小结

• 一个神经元可以有多个输入。
• 一个神经元只能有一个输出，这个输出可以同时输入给多个神经元。
• 一个神经元的w的数量和输入的数量一致。
• 一个神经元只有一个b。
• w和b有人为的初始值，在训练过程中被不断修改。
• A可以等于Z，即激活函数不是必须有的。
• 一层神经网络中的所有神经元的激活函数必须一致。

（2）神经网络的训练过程

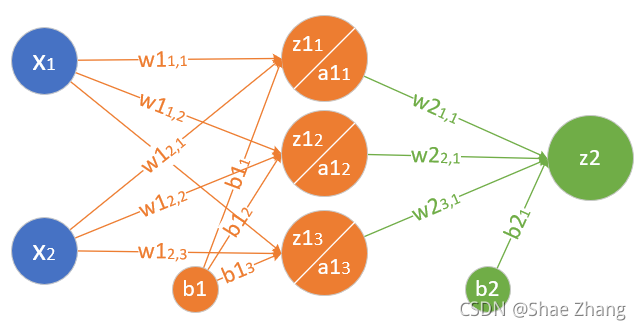
单层神经网络模型

这是一个单层的神经网络，有m个输入 (这里m=3)，有n个输出 (这里n=2)。在神经网络中，$b$ 到每个神经元的权值来表示实际的偏移值，亦即$(b_1,b_2)$，这样便于矩阵运算。也有些人把 $b$ 写成$x_0$，其实是同一个效果，即把偏移值看做是神经元的一个输入。

• $(x_1,x_2,x_3)$是一个样本数据的三个特征值
• $(w_{11},w_{21},w_{31})$是$(x_1,x_2,x_3)$到$n1$的权重
• $(w_{12},w_{22},w_{32})$是$(x_1,x_2,x_3)$到$n2$的权重
• $b_1$是$n1$的偏移
• $b_2$是$n2$的偏移
  

大家可以看到，同一个特征 $x_1$，对于$n1、n2$来说，权重是不相同的，因为$n1、n2$是两个神经元，它们完成不同的任务（特征识别）。我们假设$x_1,x_2,x_3$分别代表红绿蓝三种颜色，而 $n1,n2$ 分别用于识别暖色和冷色，那么 $x_1$ 到 $n1$ 的权重，肯定要大于 $x_1$ 到 $n2$ 的权重，因为$x_1$代表红色，是暖色。

而对于$n1$来说，$x_1，x_2，x_3$输入的权重也是不相同的，因为它要对不同特征有选择地接纳。如同上面的例子，$n1$ 对于代表红色的 $x_1$，肯定是特别重视，权重值较高；而对于代表蓝色的 $x_3$，尽量把权重值降低，才能有正确的输出。

训练流程

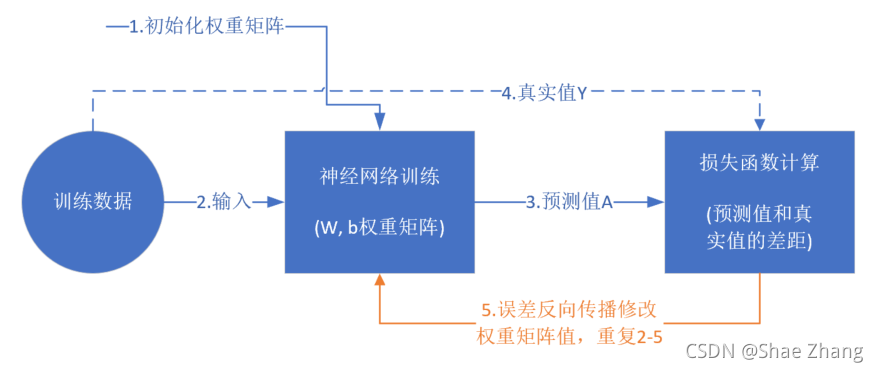
前提条件

1. 首先是我们已经有了训练数据；
2. 我们已经根据数据的规模、领域，建立了神经网络的基本结构，比如有几层，每一层有几个神经元；
3. 定义好损失函数来合理地计算误差。

步骤

假设我们有表1-1所示的训练数据样本。

表1-1 训练样本示例

其中，x1，x2，x3是每一个样本数据的三个特征值，Y是样本的真实结果值：

1. 随机初始化权重矩阵，可以根据正态分布等来初始化。这一步可以叫做“猜”，但不是瞎猜；
2. 拿一个或一批数据作为输入，带入权重矩阵中计算，再通过激活函数传入下一层，最终得到预测值。在本例中，我们先用Id-1的数据输入到矩阵中，得到一个A值，假设A=5；
3. 拿到Id-1样本的真实值Y=3；
4. 计算损失，假设用均方差函数 $Loss=(A-Y{)}^2=(5-3{)}^2=4$；
5. 根据一些神奇的数学公式（反向微分），把Loss=4这个值用大喇叭喊话，告诉在前面计算的步骤中，影响A=5这个值的每一个权重矩阵，然后对这些权重矩阵中的值做一个微小的修改（当然是向着好的方向修改，这一点可以用数学家的名誉来保证）；
6. 用Id-2样本作为输入再次训练（goto 2）；
7. 这样不断地迭代下去，直到以下一个或几个条件满足就停止训练：损失函数值非常小；准确度满足了要求；迭代到了指定的次数。

训练完成后，我们会把这个神经网络中的结构和权重矩阵的值导出来，形成一个计算图（就是矩阵运算加上激活函数）模型，然后嵌入到任何可以识别/调用这个模型的应用程序中，根据输入的值进行运算，输出预测值。

（3）神经网络中的矩阵运算

$$z{1}_1=x_1\cdot w{1}_{1,1}+x_2\cdot w{1}_{2,1}+b{1}_1$$
$$z{1}_2=x_1\cdot w{1}_{1,2}+x_2\cdot w{1}_{2,2}+b{1}_2$$
$$z{1}_3=x_1\cdot w{1}_{1,3}+x_2\cdot w{1}_{2,3}+b{1}_3$$

变成矩阵运算：

z 1 1 = ( x 1 x 2 ) ( w 1 1 , 1 w 1 2 , 1 ) + b 1 1 z1_1=

$$\begin{pmatrix} x_1 & x_2 \end{pmatrix}$$ $$\begin{pmatrix} w1_{1,1} \\ w1_{2,1} \end{pmatrix}$$ +b1_1 z11​=(x1​​x2​​)(w11,1​w12,1​​)+b11​

z 1 2 = ( x 1 x 2 ) ( w 1 1 , 2 w 1 2 , 2 ) + b 1 2 z1_2=

$$\begin{pmatrix} x_1 & x_2 \end{pmatrix}$$ $$\begin{pmatrix} w1_{1,2} \\ w1_{2,2} \end{pmatrix}$$ +b1_2 z12​=(x1​​x2​​)(w11,2​w12,2​​)+b12​

z 1 3 = ( x 1 x 2 ) ( w 1 1 , 3 w 1 2 , 3 ) + b 1 3 z1_3=

$$\begin{pmatrix} x_1 & x_2 \end{pmatrix}$$ $$\begin{pmatrix} w1_{1,3} \\ w1_{2,3} \end{pmatrix}$$ +b1_3 z13​=(x1​​x2​​)(w11,3​w12,3​​)+b13​

再变成大矩阵：

Z 1 = ( x 1 x 2 ) ( w 1 1 , 1 w 1 1 , 2 w 1 1 , 3 w 1 2 , 1 w 1 2 , 2 w 1 2 , 3 ) + ( b 1 1 b 1 2 b 1 3 ) Z1 =

$$\begin{pmatrix} x_1 & x_2 \end{pmatrix}$$ $$\begin{pmatrix} w1_{1,1}&w1_{1,2}&w1_{1,3} \\ w1_{2,1}&w1_{2,2}&w1_{2,3} \\ \end{pmatrix}$$ + $$\begin{pmatrix} b1_1 & b1_2 & b1_3 \end{pmatrix}$$ Z1=(x1​​x2​​)(w11,1​w12,1​​w11,2​w12,2​​w11,3​w12,3​​)+(b11​​b12​​b13​​)
最后变成矩阵符号：
$$Z1=X\cdot W1+B1$$
然后是激活函数运算：
$$A1=a(Z1)$$
同理可得：
$$Z2=A1\cdot W2+B2$$
注意：损失函数不是前向计算的一部分。

（4）神经网络的主要功能

回归（Regression）或者叫做拟合（Fitting）

单层的神经网络能够模拟一条二维平面上的直线，从而可以完成线性分割任务。而理论证明，两层神经网络可以无限逼近任意连续函数。

所谓回归或者拟合，其实就是给出x值输出y值的过程，并且让y值与样本数据形成的曲线的距离尽量小，可以理解为是对样本数据的一种骨架式的抽象。

分类（Classification）

（5）为什么需要激活函数

为什么需要激活函数

生理学上的例子

人体骨关节是动物界里最复杂的生理结构，一共有8个重要的大关节：肩关节、
肘关节、腕关节、髋关节、膝关节、踝关节、颈关节、腰关节。

人的臂骨，腿骨等，都是一根直线，人体直立时，也是一根直线。但是人在骨关节和肌肉组织的配合下，可以做很多复杂的动作，原因就是关节本身不是线性结构，而是一个在有限范围内可以任意活动的结构，有一定的柔韧性。

比如肘关节，可以完成小臂在一个二维平面上的活动。加上肩关节，就可以完成胳膊在三维空间的活动。再加上其它关节，就可以扩展胳膊活动的三维空间的范围。

用表1-2来对比人体运动组织和神经网络组织。

表1-2 人体运动组织和神经网络组织的对比

激活函数就相当于关节。

激活函数的作用

看以下的例子：

$$Z1=X\cdot W1+B1$$

$$Z2=Z1\cdot W2+B2$$

$$Z3=Z2\cdot W3+B3$$

展开：

Z 3 = Z 2 ⋅ W 3 + B 3 = ( Z 1 ⋅ W 2 + B 2 ) ⋅ W 3 + B 3 = ( ( X ⋅ W 1 + B 1 ) ⋅ W 2 + B 2 ) ⋅ W 3 + B 3 = X ⋅ ( W 1 ⋅ W 2 ⋅ W 3 ) + ( B 1 ⋅ W 2 ⋅ W 3 + B 2 ⋅ W 2 + B 3 ) = X ⋅ W + B

$$\begin{aligned} Z3&=Z2 \cdot W3 + B3 \\ &=(Z1 \cdot W2 + B2) \cdot W3 + B3 \\ &=((X \cdot W1 + B1) \cdot W2 + B2) \cdot W3 + B3 \\ &=X \cdot (W1\cdot W2 \cdot W3) + (B1 \cdot W2 \cdot W3+B2 \cdot W2+B3) \\ &=X \cdot W+B \end{aligned}$$ Z3​=Z2⋅W3+B3=(Z1⋅W2+B2)⋅W3+B3=((X⋅W1+B1)⋅W2+B2)⋅W3+B3=X⋅(W1⋅W2⋅W3)+(B1⋅W2⋅W3+B2⋅W2+B3)=X⋅W+B​

$Z1,Z2,Z3$分别代表三层神经网络的计算结果。最后可以看到，不管有多少层，总可以归结到$XW+B$的形式，这和单层神经网络没有区别。

如果我们不运用激活函数的话，则输出信号将仅仅是一个简单的线性函数。线性函数一个一级多项式。线性方程是很容易解决的，但是它们的复杂性有限，并且从数据中学习复杂函数映射的能力更小。一个没有激活函数的神经网络将只不过是一个线性回归模型罢了，不能解决现实世界中的大多数非线性问题。

没有激活函数，我们的神经网络将无法学习和模拟其他复杂类型的数据，例如图像、视频、音频、语音等。这就是为什么我们要使用人工神经网络技术，诸如深度学习，来理解一些复杂的事情，一些相互之间具有很多隐藏层的非线性问题。