基于MATLAB的Gough-Stewart平台六自由度机构的运动控制与仿真——正逆运动学、力学分析、关节角度求解、并联机器人运动学分析与运动控制_matlab运动仿真结论

MATLAB仿真 gough-stewart平台六自由度机构运动控制，通过运动学实现控制运动，求解正运动学、逆运动学，力学分析，求解关节角度，并联机器人运动学分析，运动学运动控制，运动模拟仿真

ID:38290671435484018

起床码MATLAB

---

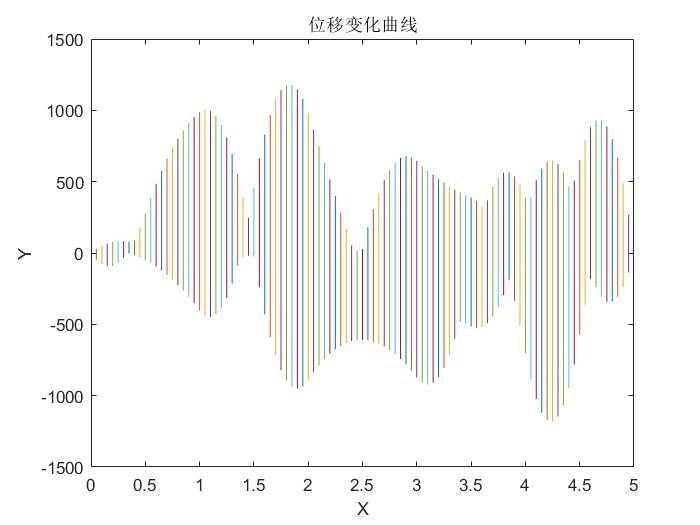
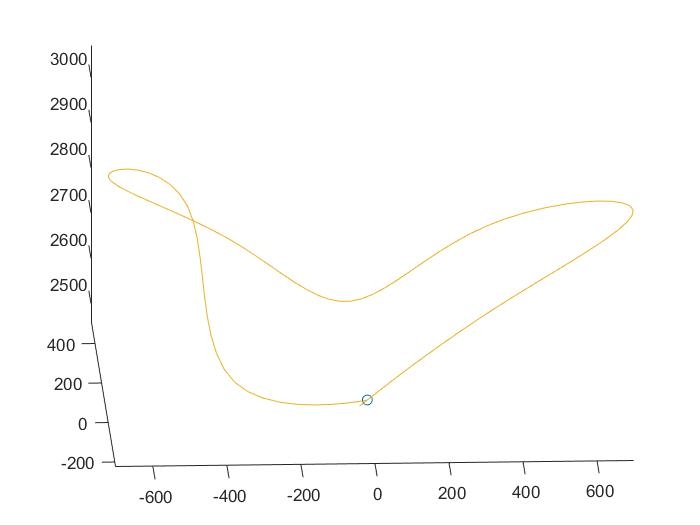
标题：Gough-Stewart平台六自由度机构的MATLAB仿真与运动控制

摘要：本文通过MATLAB仿真研究Gough-Stewart平台六自由度机构的运动控制。首先，利用运动学方法求解机构的正运动学和逆运动学问题，实现对机构运动的精确控制。然后，进行力学分析，求解机构的关节角度，并分析并联机器人的运动学特征。最后，基于运动学模型，我们进行了运动控制的仿真模拟，验证了所提出的方法的可行性和有效性。

1. 引言
   随着工业自动化的发展，机器人技术在制造业、医疗行业等领域得到了广泛应用。Gough-Stewart平台作为一种常见的并联机构，具有结构刚性好、承载能力强、运动范围广等特点，被广泛应用于航空航天、船舶制造等领域。本文以Gough-Stewart平台六自由度机构为研究对象，通过MATLAB仿真实现对其运动控制的深入研究。

2. Gough-Stewart平台六自由度机构的运动学实现
   2.1 正运动学问题
   正运动学是指通过已知机构的关节角度以及初始位置和姿态信息，求解机构末端执行器的位置和姿态信息。本文基于解析解法和迭代法两种方法进行正运动学求解。其中，解析解法通过建立Gough-Stewart平台六自由度机构的几何模型和运动学方程，直接求解末端执行器的位置和姿态。迭代法则通过逐次迭代优化机构的位置和姿态，最终得到准确的正运动学解。

2.2 逆运动学问题
逆运动学是指通过已知机构的末端执行器的位置和姿态信息，求解机构的关节角度。本文利用解析解法和数值解法两种方法进行逆运动学求解。其中，解析解法通过建立Gough-Stewart平台六自由度机构的逆运动学方程，直接求解关节角度。数值解法则利用牛顿-拉夫逊方法和遗传算法等数值优化方法，通过迭代计算得到准确的逆运动学解。

3. Gough-Stewart平台六自由度机构的力学分析
   力学分析是对机构的力学特性进行研究和分析，包括静力学和动力学分析。本文通过建立机构的动力学模型，推导机构的关节力和力矩方程，分析机构在不同工况下的力学特性。同时，通过求解关节角度，得到机构的关节力矩分布图，并对机构的承载能力进行评估。

4. 并联机器人的运动学分析
   并联机器人是指由多个独立机构组成的机器人系统，具有并联的特点。本文通过运动学分析，研究并联机器人的运动学特征。首先，通过建立并联机器人的运动学模型，推导出机器人末端执行器的位置和姿态方程。然后，通过求解关节角度，得到机器人的关节运动规律。最后，通过运动学仿真，验证并联机器人的运动特性和控制效果。

5. 运动控制的仿真模拟
   基于所建立的运动学模型，本文进行了运动控制的仿真模拟。首先，建立机构的控制器模型，设计合适的控制算法和参数。然后，通过MATLAB仿真平台，模拟机构的运动控制过程，并分析系统的动态响应和稳定性。最后，通过对比实验，验证所提出的运动控制方法的可行性和有效性。

结论：本文对Gough-Stewart平台六自由度机构的MATLAB仿真与运动控制进行研究。通过运动学分析和力学分析，求解了机构的正逆运动学问题，并研究了机构的力学特性。同时，对并联机器人的运动学特性进行了深入研究。最后，通过仿真模拟验证了所提出的运动控制方法的可行性和有效性。本文的研究结果对于提升机器人的运动控制精度和稳定性具有一定的参考价值。

关键词：Gough-Stewart平台、六自由度机构、MATLAB仿真、正逆运动学、力学分析、并联机器人、运动控制

以上相关代码,程序地址：http://matup.cn/671435484018.html