热门标签
热门文章
- 1爬虫实战系列(十一):Win10下手机爬虫工具appium的安装与测试_安卓爬虫实战案例
- 2六、项目发布-- 3. Node.js+express 编写书城首页API
- 3netbios 网上基本输入输出系统 简介_netbios-ns
- 4Hugging Face实战-系列教程19:文本摘要建模实战1 之 数据清洗(中文商城评价数据处理方法)_huggingface 本地数据怎么处理
- 5vue+element表格使用(单元格内编辑、表格后新增一行、删除表格行)_cell-dblclick获取选中
- 6【存储】块存储、文件存储和对象存储的区别?
- 7创建vue3+ts项目_vue3+ts 创建项目
- 8echarts如何实现3D饼图(环形图)?_echarts环形图3d
- 92024年第十五届蓝桥杯C/C++B组复盘(持续更新)_2024蓝桥杯c语言题型
- 10解决VS中scanf()函数报错问题的四种方案(详细)_scanf报错
当前位置: article > 正文
【leetcode C++】滑动窗口
作者:weixin_40725706 | 2024-04-10 21:51:09
赞
踩
【leetcode C++】滑动窗口
1. LCR 008. 长度最小的子数组
题目
给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0 。
题目链接
画图 和 文字 分析
先说说有关滑动窗口的知识
滑动窗口特征和步骤:
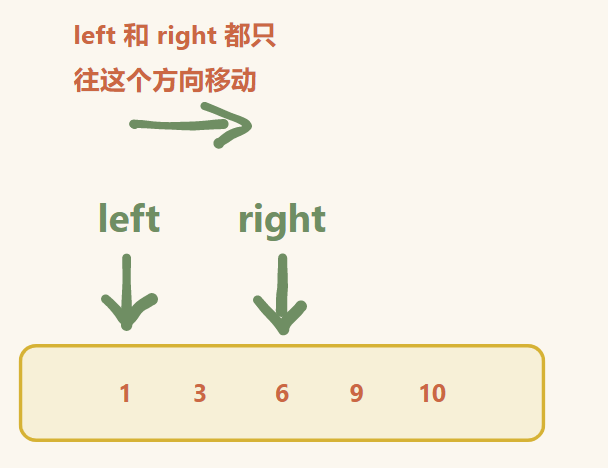
- 无论是出窗口,还是进窗口,都是往一个方向上移动(不会后退)
- 步骤:
- 进窗口
- 检查
- 出窗口
- 更新数据(具体放的位置因题而异)
回到这道题,为什么符合滑动窗口的思想呢?
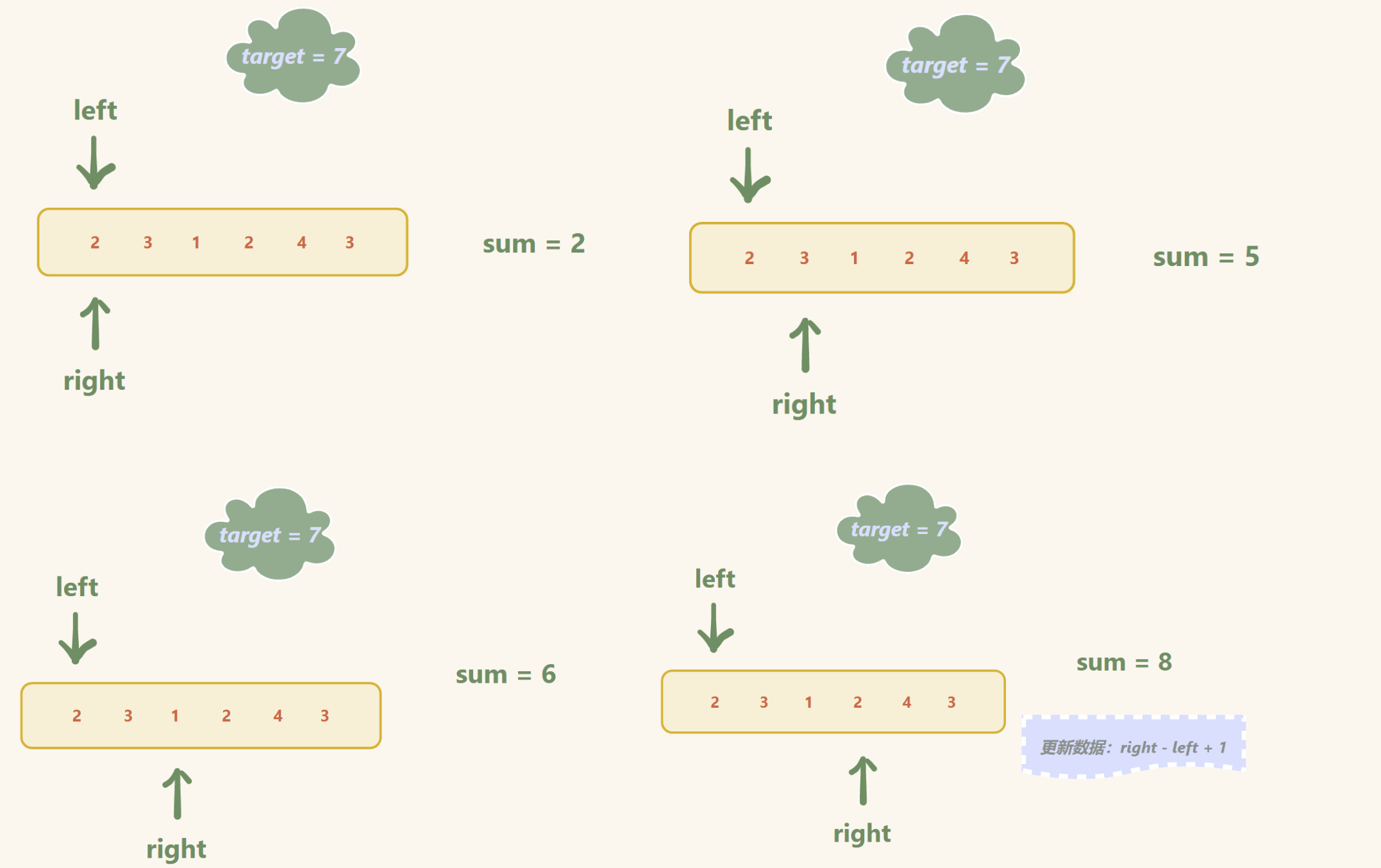
让 left = 0 , right = 0
通过 right 遍历数组 ,得到区间的所有数之和 sum
sum 与 target 相比
- 如果 sum < target
right++(进窗口)
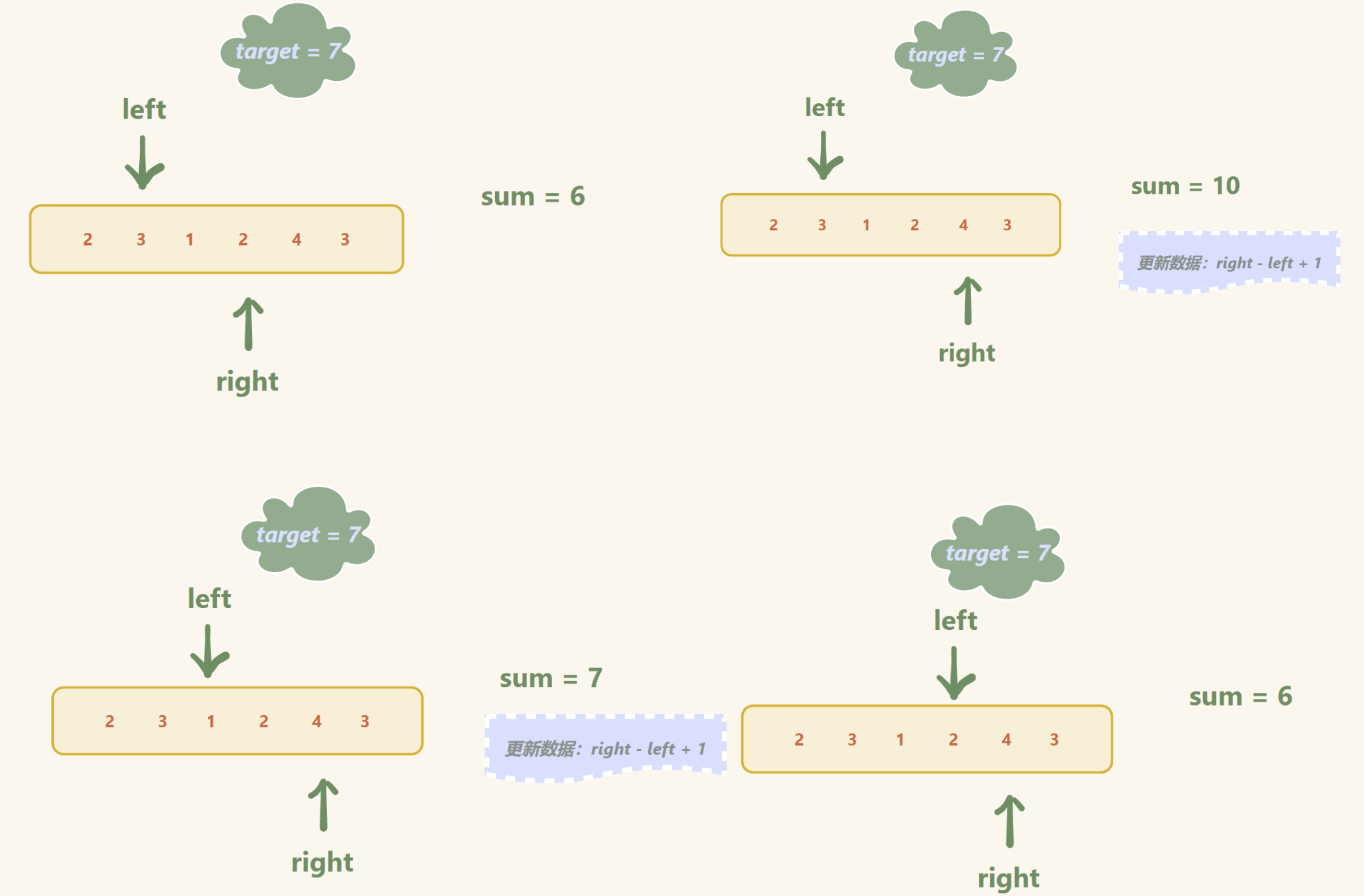
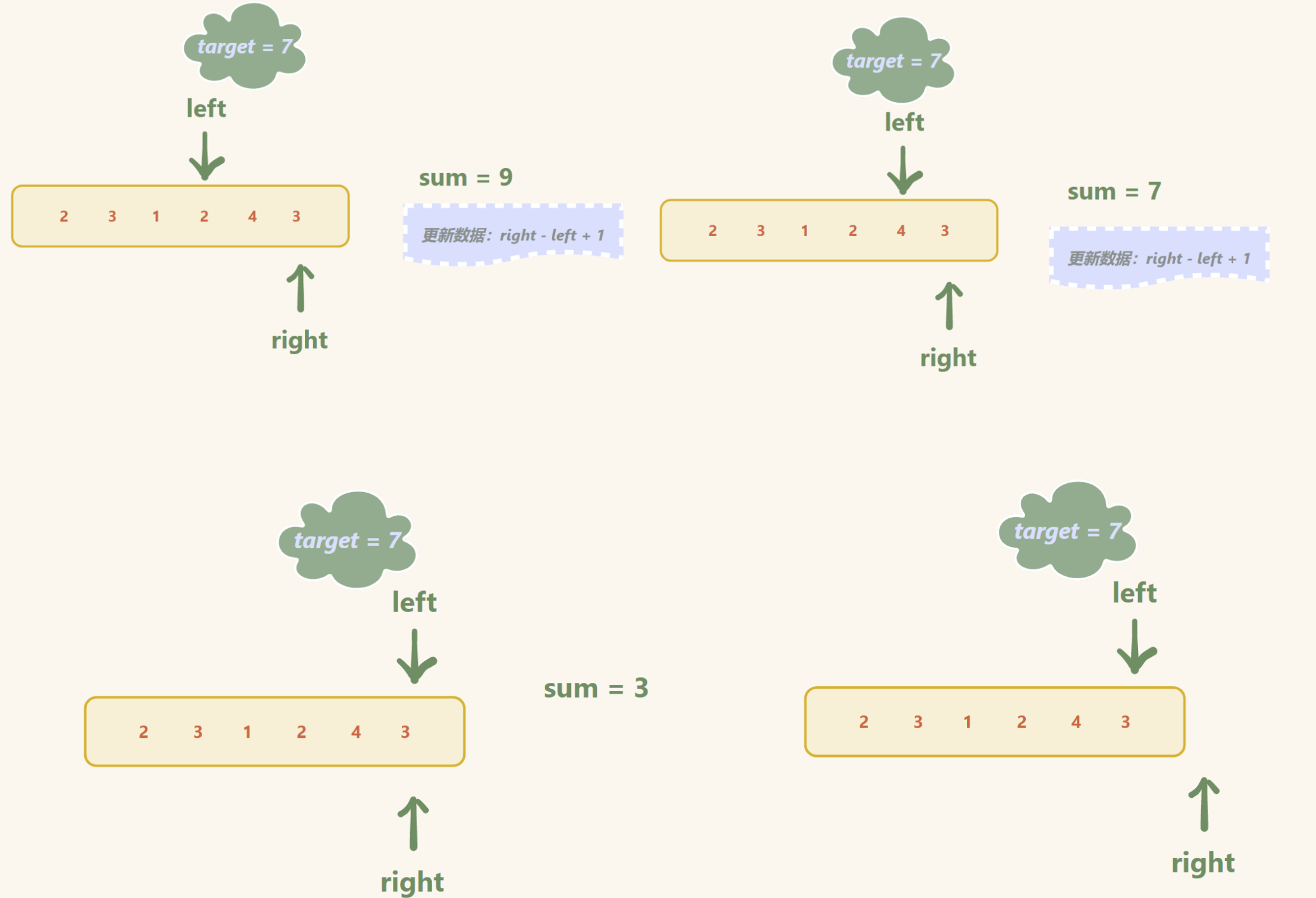
2. 如果 sum >= target (检查)
记录此时的区间长度 (更新数据)
left++(出窗口), sum -= (left 之前所指向的数),直到 回到第一种情况(里层循环结束条件)
外层循环结束条件(right >= n)
注意:
- 记录我们用 count 表示,由于求最小长度,count 的初始化为 INT_MAX , 如果最后没有进入更新数据那一块(整个数组之和 < target),记得判断 count 的值
举例:
输入:target = 7, nums = [2,3,1,2,4,3]
输出:2
代码
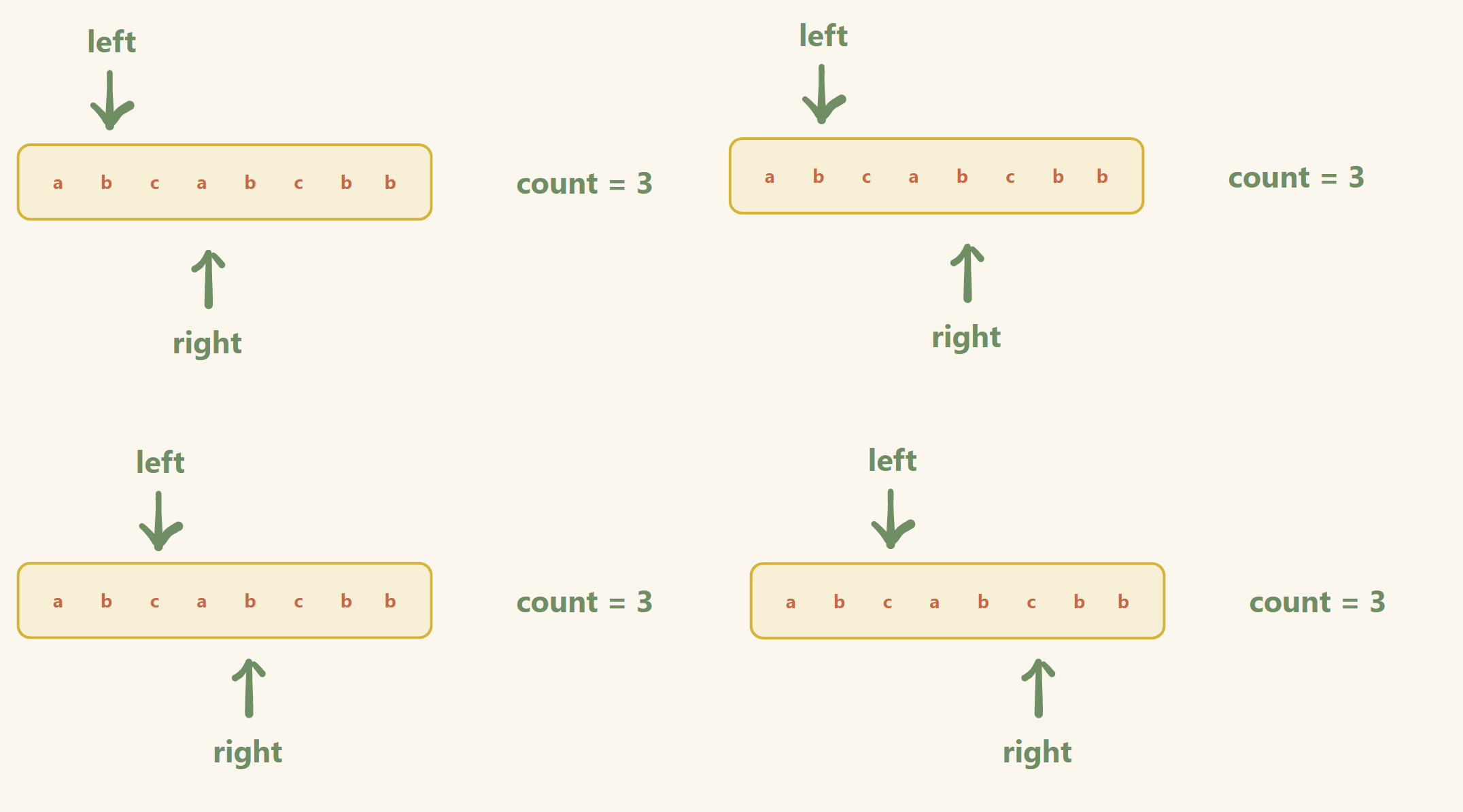
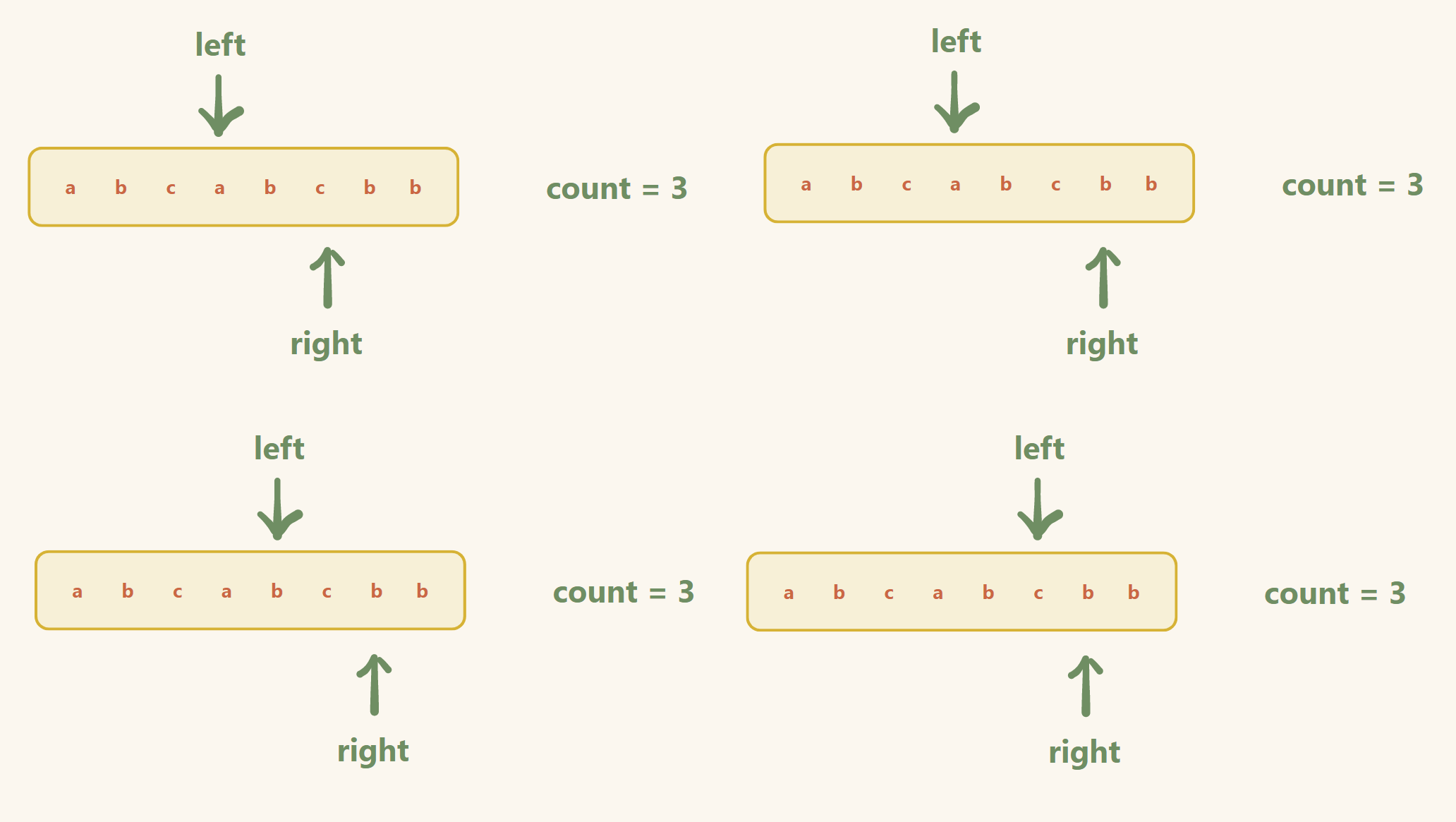
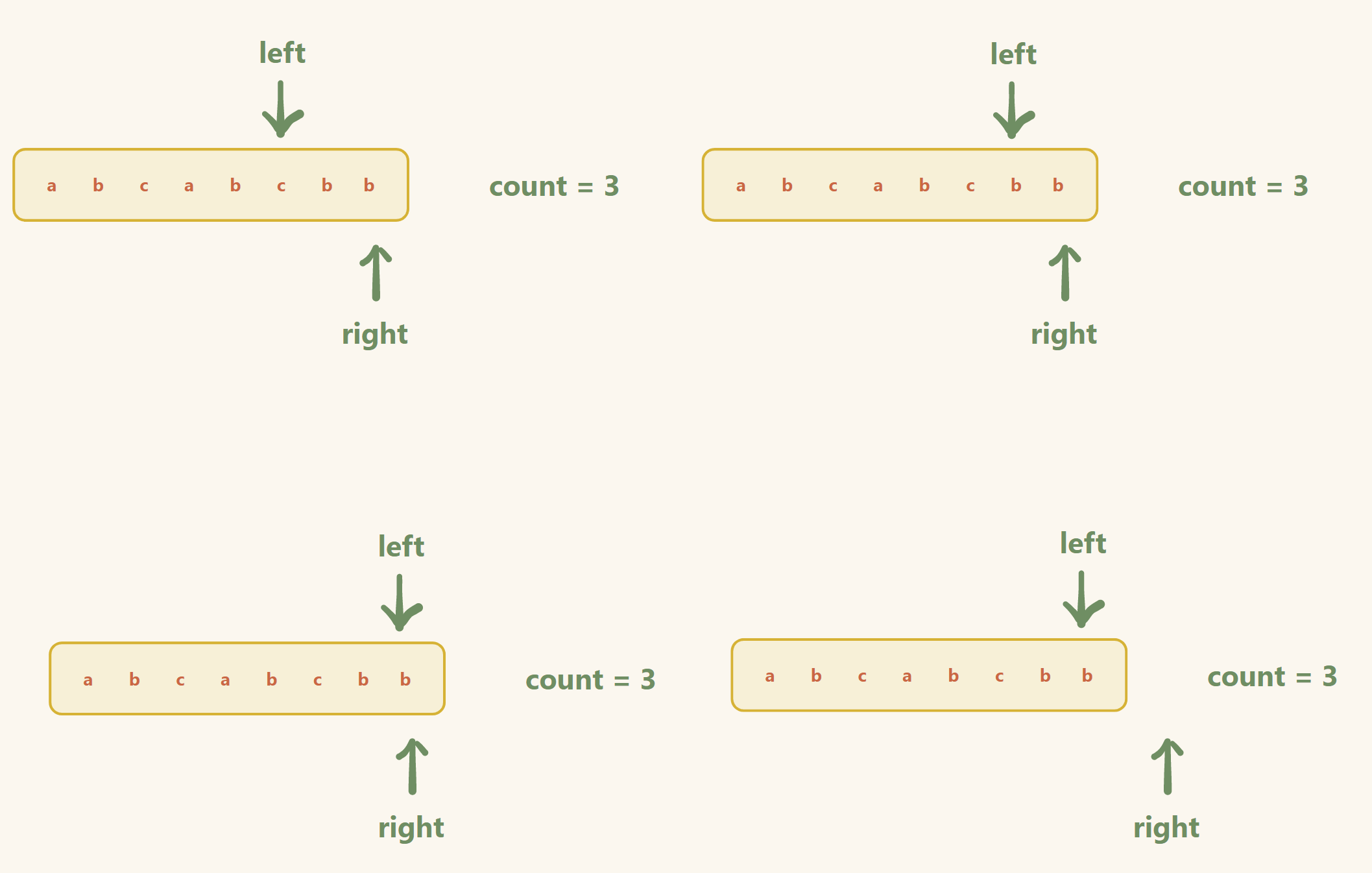
2. LCR 016. 无重复字符的最长子串
题目
给定一个字符串 s ,请你找出其中不含有重复字符的 最长连续子字符串 的长度。
题目链接
画图 和 文字 分析
步骤:
定义两个指针 , left = 0 , right = 0 , hash数组(存放字符的个数)
- 当 hash[right] <= 1
right++(进窗口)
2. 当 hash[right] > 1(出窗口)
更新数据
left++ ,同时 hash[left - 1]-- ,直到回到第一种情况(里层循环结束条件)
外层结束条件(right >= n)
注意:
- 这种方法存在遗漏的情况,跳出整个循环后,一定要最后更新一下(如果碰到整个数组都没有重复元素的情况,不最后检查一下就是错误的)
- 如果不想实现注意事项一,那么把更新数据提前到进窗口那一步即可
举例:(题解二的做法)
输入: s = "abcabcbb"
输出: 3
代码
声明:本文内容由网友自发贡献,不代表【wpsshop博客】立场,版权归原作者所有,本站不承担相应法律责任。如您发现有侵权的内容,请联系我们。转载请注明出处:https://www.wpsshop.cn/w/weixin_40725706/article/detail/401170
推荐阅读
相关标签