【优化求解】遗传算法结合粒子群算法求解单目标优化问题【含Matlab源码 1659期】_遗传算法和粒子群算法结合

⛄一、GA-PSO混合优化算法的基本思想

对于遗传算法来讲, 传统的遗传算法中变异算子是对群体中的部分个体实施随机变异, 与历史状态和当前状态无关。而粒子群算法中粒子则能保持历史状态和当前状态。遗传算法的进化初期, 变异有助于局部搜索和增加种群的多样性;在进化后期, 群体已基本趋于稳定, 变异算子反而会破坏这种稳定。变异概率过大会使遗传模式遭到破坏, 过小又会使搜索过程缓慢甚至停滞不前。本文通过在粒子群算法中引入遗传算法的交叉操作, 改进种群分割策略, 且用粒子群算法重构变异算子来进行算法的改进。本文所提的混合算法主要就是从用遗传算法来模拟粒子群算法的角度出发, 利用粒子群算法来重构遗传算法算子和进行种群分割。从宏观上来看, 其行为是粒子群算法;从微观来看, 其行为是遗传算法, 从而构成遗传-粒子群混合算法。下面主要介绍一下引入的交叉和变异算子及变异算子。

1 交叉算子
设GA-PSO混合算法总的进化代数为T, 当算法进化到第t代时, 总的种群设为∏t={x1t, …, xit, …, xnt}, (1≤i≤n) , n为种群规模, xit为单个粒子, 且对于任意i, (1≤i≤n) , 都有xit≤xjt成立, 即∏t有序。由于所讨论的混合算法的个体编码采用了实值编码, 且该算法主要针对于数值优化问题故交叉算子采用了算术交叉。
假设在两个个体xit, xjt (i≠j) 之间进行算术交叉, 则交叉运算后所产生的两个新个体是:

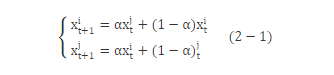
式 (2-1) 中, α为一参数, 若α是一个常数, 此时所进行的交叉运算称为均匀算术交叉;也可以是一个由进化代数决定的变量, 此时进行的是非均匀算