【深度学习-第3篇】使用MATLAB快速实现CNN分类（模式识别）任务，含一维、二维、三维数据演示案例_matlab cnn

在本文中，我们将介绍如何使用 MATLAB 中的 Convolutional Neural Network（CNN）进行分类任务。我们将使用 MATLAB 的 Deep Learning Toolbox 来创建、训练和评估 CNN。

一、一个简单的案例

1 安装和准备

首先，确保已安装 MATLAB 的 Deep Learning Toolbox，且需要使用MATLAB2018a及以上版本。不过这里个人建议大家用2022以上版本的MATLAB，因为低版本的MATLAB运行可能会报以下这个警告，对程序运行效率影响还是较大的。

低版本MATLAB运行深度学习可能会报的错误

然后，我们需要准备一组图像数据用于训练和测试。在本教程中，我们将使用 MNIST 数据集。MNIST 数据集包含 70,000 张手写数字的灰度图像 (0-9)，其中 60,000 张用于训练，10,000 张用于测试。

2 加载数据

使用 Deep Learning Toolbox 中的digitTrain4DArrayData和digitTest4DArrayData函数加载MNIST数据集。

% 加载 MNIST 数据
[XTrain, YTrain] = digitTrain4DArrayData;
[XTest, YTest] = digitTest4DArrayData;

3 创建 CNN 模型

接下来，我们创建一个简单的 CNN 模型。这里我们使用一个较小的网络结构，以便在本教程中快速进行训练。

% 定义 CNN 模型结构
layers = [
    imageInputLayer([28 28 1], 'Name', 'input')
 
    convolution2dLayer(3, 8, 'Padding', 'same', 'Name', 'conv1')
    batchNormalizationLayer('Name', 'bn1')
    reluLayer('Name', 'relu1')
 
    maxPooling2dLayer(2, 'Stride', 2, 'Name', 'maxpool1')
 
    convolution2dLayer(3, 16, 'Padding', 'same', 'Name', 'conv2')
    batchNormalizationLayer('Name', 'bn2')
    reluLayer('Name', 'relu2')
 
    maxPooling2dLayer(2, 'Stride', 2, 'Name', 'maxpool2')
 
    fullyConnectedLayer(64, 'Name', 'fc1')
    reluLayer('Name', 'relu3')
 
    fullyConnectedLayer(10, 'Name', 'fc2')
    softmaxLayer('Name', 'softmax')
    classificationLayer('Name', 'classification')];

此时我们可以看一下这个网络结构：

disp(layers)

执行完上述代码，将打印出网络结构：

对于网络结构中各个层的含义，以及层中各种参数的含义，大家可以看我之前写的这篇文章：

Mr.看海：【深度学习-第2篇】CNN卷积神经网络30分钟入门！足够通俗易懂了吧（图解）

使用下边代码，可以可视化上述网络结构：

layerGraph = layerGraph(layers);
figure
plot(layerGraph);

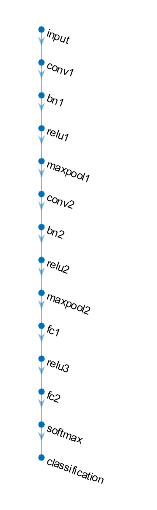
网络结构图，在网络结构更加复杂时，该图会比较有用

这里回答几个大家可能会有疑问的问题：

(1).怎么冒出来一个之前没讲过的batchNormalizationLayer？

batchNormalizationLayer层的作用是对网络中的每个 mini-batch 数据进行归一化，即让每个特征的均值为0，方差为1。这样做可以使得网络训练更加稳定，减少梯度消失和梯度爆炸的问题，同时还可以提高网络的泛化能力，防止过拟合。

在 MATLAB 中，使用 batchNormalizationLayer 函数可以创建一个批量归一化层。这个层放在convolution2dLayer之后，是CNN在MATLAB中常用使用方式，照此设置即可。更多说明可以看这里：Batch normalization layer。

(2).如果我输入的不是二维数据，而是一维数据或者三维数据，该怎么办？

对于一维数据，也可以看成是其中一个维度的长度为1的二维数据，所以依旧可以使用imageInputLayer，只不过在设置卷积尺寸和池化尺寸的时候需要注意对应的维度也应该为1。

对于三维数据，就可以看作是一个多通道的图片，同样也可以用imageInputLayer。

不过需要注意的是，imageInputLayer需要给定输入数据的尺寸，比如上边例子中就是[28,28,1]，也就是代表长宽分别为28的单通道，如果输入的是一维数据（比如长度是10），那么这个尺寸可能就是[10,1,1]了，三维数据同理。

(3).我知道CNN常被拿来做分类，可是我就是想用它做预测，该怎么办？

虽然CNN主要用于（图像）分类，但它也可以用于其他任务，如回归问题、时间序列预测等。要使用CNN进行预测，需要根据您的具体任务对网络结构进行一些调整。对于执行回归预测和时间序列预测的CNN程序，我们后边会专门出文章介绍的。

4.设置训练参数

options = trainingOptions('sgdm', ... %训练算法 (使用随机梯度下降法，包含动量项)
 'ExecutionEnvironment','auto', ...   %训练执行环境
 'GradientThreshold',Inf, ...         %梯度阈值
 'MaxEpochs',30, ...                  %最大迭代次数
 'InitialLearnRate',0.001, ...        %初始学习率
 'MiniBatchSize',16, ...              %小批量数据的大小
 'LearnRateSchedule','piecewise', ... %学习率的调整策略
 'LearnRateDropFactor',0.9, ...       %调整因子
 'LearnRateDropPeriod',10, ...        %调整周期
 'SequenceLength','longest', ...      %序列长度
 'Shuffle','every-epoch', ...         %数据的混洗方式
 'Verbose',1, ...                     %是否显示训练过程中的详细信息
 'Plots','training-progress');        %是否绘制训练进度图表

这段代码是使用 MATLAB 的深度学习框架来配置神经网络训练的参数。它创建了一个名为 options 的训练选项对象，这个对象包含了一系列用于训练神经网络模型的参数设置。

这些参数将会影响神经网络训练的效率和结果。通过调整这些参数，我们可以优化模型的训练过程，以得到更好的模型效果。

展开说的话，其中每个参数的具体含义如下：

'sgdm'：这是训练算法，'sgdm' 代表带有动量的随机梯度下降（Stochastic Gradient Descent with Momentum）。这是一种常用的优化算法。
'ExecutionEnvironment', 'auto'：此选项指定了训练算法的执行环境。可选值包括 'auto'，'cpu'，'gpu' 和 'multi-gpu'。其中，'auto' 表示 MATLAB 自动选择最佳环境，'cpu' 和 'gpu' 分别表示在 CPU 或 GPU 上执行训练，而 'multi-gpu' 表示在多个 GPU 上执行训练。
'GradientThreshold', Inf：这个参数设置了梯度裁剪阈值，当梯度的绝对值超过此阈值时，梯度将被裁剪。这是防止梯度爆炸的一种方法。在这个例子中，阈值设置为 Inf，意味着梯度裁剪实际上没有被激活。
'MaxEpochs', 30：此参数设定了模型训练的最大迭代次数。一次迭代（也称 epoch）意味着模型已经完整地学习过一次完整的训练集。在这个例子中，模型将会进行 30 次迭代。
'InitialLearnRate', 0.001：此参数设定了学习率的初始值。学习率是优化算法的一个重要参数，决定了模型参数更新的步长。如果学习率太大，可能导致模型无法找到最优解；如果学习率太小，可能导致模型收敛速度过慢。
'MiniBatchSize', 16：此参数设定了每次训练的小批量数据的大小。使用小批量可以加快模型训练速度，并且可以增加训练过程的随机性，有助于提高模型的泛化能力。
'LearnRateSchedule', 'piecewise'：此参数设定了学习率的调整策略。'piecewise' 表示分段恒定策略，即在特定的迭代次数，学习率会乘以一个因子（由 'LearnRateDropFactor' 参数设定）。
'LearnRateDropFactor', 0.9：此参数设定了学习率调整的因子，只在 'LearnRateSchedule' 参数设定为 'piecewise' 时有效。在每个 'LearnRateDropPeriod' 周期后，学习率会乘以这个因子。
'LearnRateDropPeriod', 10：此参数设定了学习率调整的周期，只在 'LearnRateSchedule' 参数设定为 'piecewise' 时有效。每过这么多个迭代周期，学习率会按照 'LearnRateDropFactor' 设定的因子进行调整。
'SequenceLength', 'longest'：此参数设定了序列处理方式，可选值有 'longest'，'shortest' 或一个正整数。'longest' 表示使用最长的序列长度，'shortest' 表示使用最短的序列长度，指定一个正整数则表示所有的序列都将被填充或者截断到这个长度。
'Shuffle', 'every-epoch'：此参数设定了训练数据的混洗策略。'every-epoch' 表示在每次迭代开始时都会重新混洗训练数据。这可以增加训练的随机性，有助于提高模型的泛化能力。
'Verbose', 1：此参数设定是否在训练过程中打印详细信息。如果设定为 1，那么在每次迭代完成后都会打印出一些信息，例如当前的迭代次数、损失函数的值等。
'Plots', 'training-progress'：设置了是否在训练过程中显示训练进度的图表，如果不显示，可以设置为'none'。

虽然这些设置内容看起来蛮多，但是真正核心的是以下这几个参数，在网络调试过程中，需要重点调试：

'MaxEpochs'：最大迭代次数决定了模型在训练集上学习的次数。如果设定的迭代次数太少，模型可能无法充分学习；反之，如果迭代次数过多，可能会导致过拟合。
'InitialLearnRate'：初始学习率对模型的训练速度和效果有很大影响。学习率太大可能会导致模型无法收敛，学习率太小则可能导致训练速度过慢。此外，学习率的设定也会影响到学习率调整策略的效果。
'MiniBatchSize'：小批量大小影响了每次参数更新的计算效率和准确性。较小的批量大小可以增加模型训练的随机性，有助于防止过拟合，但也可能导致训练过程变慢。
'LearnRateSchedule'， 'LearnRateDropFactor'， 'LearnRateDropPeriod'：这三个参数共同设定了学习率的调整策略。适当的调整学习率可以帮助模型更快地收敛，并达到更好的效果。

二、“一行代码”实现CNN分类任务

上边章节演示了使用MATLAB实现CNN分类的基础代码演示，不过我们在实际研究中可能会面临更为复杂的困境：

• 导入自己的数据后，网络结构一改就频频报错
• 代码被改得乱七八糟，看的头大
• 不知道该画哪些图、怎么画图
• 一维数据分类不知道怎么搞
• ……

按照本专栏的惯例，笔者封装了快速实现CNN分类的函数，在设定好相关参数后，只需要一行代码，就可以实现数据集训练集/验证集/测试集快速划分、绘制混淆矩阵、计算分类准确度，导出训练过程数据等等常用功能，而且这个封装函数可以适用于一维/二维/三维数据，这个函数的介绍如下：

[accuracy,recall,precision,net,info] = FunClassCNNs(dataX,dataY,divideR,conLayer,poolingLayer,fcLayer,options,figflag)
% 使用CNN进行模式识别（分类）的快速实现函数
% 该函数需要输入的数据为array数组型，如果是图片数据则需要通过imread等方式进行读取转换
% 输入：
% dataX：输入数据，R1*R2*R3*Q的矩阵，Rn为输入数据的维度，Q为批次数，输入该变量时一定要注意维度正确
% 例1：对于3通道的图像数据，例如长28像素，宽28像素，共5000组数据，则dataX的维度为：28*28*3*5000
% 例2：对于一维数组，每组数据长度为20，共1000组数据，则dataX的可以维度为：1*20*1*1000或20*1*1*1000
% dataY：标签值，可以为两种方式：
%                              向量型：U*Q的矩阵，U为标签种类数，Q为批次数
%                              索引型：1*Q的矩阵，Q为批次数
% divideR：数据集（训练集、验证集、测试集）划分比例，如：divideR =[0.6,0.2,0.2]，
% 则代表60%数据用于训练集，20%数据用于验证集，20%数据用于测试集
 
% cLayer：卷积层结构，为n*5的二维数组，其中n为卷积层的数量
% 列向的5个维度时分别代表滤波器的高、滤波器的宽、滤波器数量、步长、填充
% 例1，cLayer =
% [3,16,1,1;3,32,1,0]时，则代表有两层卷积层，其中第一层滤波器高为3，宽为3，滤波器数量为16，步长1，填充1
%                                                第二次滤波器高为3，宽为3，滤波器数量为32，步长1，填充0
% 例2，cLayer =
% [3,1,16,1,1;3,1,32,1,0]时，则代表有两层卷积层，其中第一层滤波器高为3，宽为1，滤波器数量为16，步长1，填充1
%                                                第二次滤波器高为3，宽为1，滤波器数量为32，步长1，填充0
 
% poolingLayer：池化层结构，为长度为n*5的cell数据，其中n为池化层的数量，和卷积层层数相同。
% 列向的三个维度分别代表：1.池化层类型，分为'maxPooling2dLayer'和'averagePooling2dLayer'两种，如果不用池化层设置为'none'
%                         2.池化区域高度尺寸
%                         3.池化区域宽度尺寸
%                         4.步长
%                         5.填充
% 例如：
% poolingLayer = {'maxPooling2dLayer',2,2,2,1; 'averagePooling2dLayer',2,2,1,0};
% 代表第一个池化层为最大池化层，尺寸为2*2，步长2，填充1，第二个池化层为平均池化层，尺寸为2*2，步长1，填充0
% 注意！如果对应卷积层后不设置池化层，请在对应的位置设置为'none',0,0,0,0
% 比如cLayer设置为两层时，如果只想在第一层卷积层后对应有池化层，第二层卷积层后无池化层，那么池化层应该设置为：
% poolingLayer = {'maxPooling2dLayer',1,2,1,0;
%                 'none',0,0,0,0 }; %后边的四个0主要是占位，不起实际作用
 
% options：一些与网络训练等相关的设置，使用结构体方式赋值，比如 options.MaxEpochs = 1000，具体包括：
%             solverName：求解器，'sgdm'（默认） | 'rmsprop' | 'adam'
%             MaxEpochs：最大迭代次数，默认30
%             MiniBatchSize：批尺寸，默认128
%             GradientThreshold：梯度极限，默认为Inf
%             InitialLearnRate：初始化学习速率（默认0.005）
%             Plots：是否显示训练过程，'none' 为不显示（默认） | 'training-progress'为显示
%             ValidationFrequency：验证频率，即每间隔多少次迭代进行一次验证，默认50
%             LearnRateSchedule：即LearnRateSchedule是否在一定迭代次数后学习速率下降， LearnRateSchedule ='piecewise'为使用，'none'为不使用（默认）
%             LearnRateDropPeriod：即LearnRateDropPeriod学习速率下降时的迭代数，默认为10
%             LearnRateDropFactor：即LearnRateDropFactor学习速率下降因子，下降后变为LearnRateDropFactor*InitialLearnRate，LearnRateSchedule为0时可以赋0，默认为0.1
%             （未启用）NorFlag：即Normalization Flag，设置为1时则在程序中进行数据归一化和反归一化操作，否则不进行，建议设置为1
%             SeedFlag：随机种子标志，设置为1时启用随机种子,(默认为1)
% fcLayer：全连接层，可以设置多层，如果设置fcLayer=[]，则在网络结构中只包含一个全连接层，输出的维度与数据类别相同。
%                                  如果设置fcLayer为数组，则代表在上边的全连接层之前再加入对应数量的全连接层和ReLU层
%                                  例如设置fcLayer=[32,16]，则代表在共有三个全连接层，第一个是fullyConnectedLayer(32)+ReLU，第二个是fullyConnectedLayer(16)+ReLU，
%                                                           第三个是fullyConnectedLayer(numClasses)
% figflag：是否画图，'on'为画图，'off'为不画
% 输出：
% accuracy：测试集分类正确率
% recall： 召回率
% precision： 精确率
% net：训练好的网络
% info：神经网络训练相关参数，如loss值、准确度等

看注释写的蛮多的似乎有点唬人，其实使用起来蛮简单。

下边我使用三个公开数据集，分别演示这个函数在一维、二维、三维数据中的应用效果，以及能够得出的一系列有用的图片和其他结果。

1.MNIST手写数据集

这就是上个章节中用到过的数据集。

MNIST手写数据集，每张图片是28*28的数据矩阵

现在我们实现分类任务，只需要执行下边这几行代码即可（全套运行程序下载链接见文末）：

%% 1.加载数据
load aMNIST-4D.mat %加载mnist数据
%% 2.调用函数进行分类
divideR = [0.6,0.2,0.2];  %训练集/验证集/测试集比例
figflag = 'on';           % 是否画图，'on'为画图，'off'为不画
% 指定训练选项
options.MaxEpochs = 50;    %最大迭代次数，默认30
options.InitialLearnRate = 0.02; %初始化学习速率（默认0.005）
options.Plots = 'training-progress'; %是否显示训练过程，'none' 为不显示（默认） | 'training-progress'为显示
options.ValidationFrequency = 10;   %验证频率，即每间隔多少次迭代进行一次验证
options.LearnRateSchedule = 'piecewise'; %是否在一定迭代次数后学习速率下降
options.LearnRateDropFactor = 0.9;  %学习速率下降因子
options.LearnRateDropPeriod = 100;   %学习速率下降时的迭代数
% 网络结构设置
conLayer = [3,3,16,1,0;   %第一层滤波器高为3，宽为3，滤波器数量为16，步长1，填充1
            3,3,32,1,0];  %第二次滤波器高为3，宽为3，滤波器数量为32，步长1，填充0
poolingLayer = {'maxPooling2dLayer',2,2,1,0;  %第一个池化层为最大池化层，尺寸为2*2，步长1，填充0
                'maxPooling2dLayer',2,2,1,0}; %第二个池化层为平均池化层，尺寸为2*2，步长1，填充0
fcLayer = [];  %不再额外设置全连接层
% 调用函数进行分类
[accuracy,recall,precision,net,info] = FunClassCNNs(dataX,dataY,divideR,conLayer,poolingLayer,fcLayer,options,figflag);

运行完上述代码后，可以得到以下结果：

（1）混淆矩阵图片。

混淆矩阵（Confusion Matrix）是一种常用的评估分类模型性能的工具。就像下图，结果是一个正方形矩阵。其中每一列对应一个实际类别，每一行对应一个预测类别。对角线绿色部分代表预测结果与实际类别相同（即预测正确）的数量和比例，红色部分则代表预测错误的数量和比例。

比如第3行第4列红色方框中的数字1，代表对于本次分类，有一个手写数字“3”被分类成了“2”。

解读混淆矩阵的关键是观察对角线元素和非对角线元素。在对角线上的元素表示正确分类的样本数量，而非对角线上的元素表示被误分类的样本数量。

最下边一行代表了“每类数据实际识别成功的比例”；最右边一列“分类为该类别的数据中实际属于该类别的比例”，稍微有点绕，大家可以多念几遍。。。

最右下角的数据及全体数据的识别准确率。

需要注意的是，这个图针对的是测试集数据。

混淆矩阵可以全面地描述分类网络的特性，属于写论文必备图片。

混淆矩阵

（2）训练过程图。

这张图片在程序运行的阶段就在不断更新迭代，上下两张图分别是分类准确度和loss值的收敛过程。其中蓝色线条是训练集结果，黑色线条是验证集结果。

如果嫌这张图丑的，同学们也可以用导出的训练过程数据自己画图，程序运行完之后，相关数据在MATLAB工作区的info变量里可以找到。

此图也是论文必画图之一。

训练过程图

（3）网络结构图、表。

这张图包含了网络结构图，以及每层网络的名称、类型、参数属性等信息表格。方便大家论文中使用。

（4）每层网络的输出尺寸。

在做CNN网络结构设计的时候，随着层数的叠加，每个特征图的尺寸越来越小，有时候一不小心就会使特征图的尺寸变为负数，然后程序自然会报错。

为了解决这个问题，笔者特地加了一个功能，可以计算出数据经过每层网络之后输出的特征图的尺寸，就像下图这样：

该结果会在命令行窗口打印出来

在实际调试过程中，你会发现这个功能非常好用。

上边这个MNIST数据集测试集正确率是98.9%，这个是随意调了调网络和参数的结果，如果花时间进一步优化网络，可以得到更好的结果。

2.CIFAR-10数据集

CIFAR-10数据集包含10个类别的32x32彩色图像。

CIFAR-10的类别包括 "airplane", "automobile", "bird", "cat", "deer", "dog", "frog", "horse", "ship", "truck"，也就是飞机、汽车、鸟、猫、鹿、狗、青蛙、马、船、卡车。

下图是其中随机抽取的一些示意图片：

CIFAR-10数据集，10个类别分别抽取了10张图

对于每个彩色图像，其数据结构就是32*32*3的一个三维矩阵了，对于10000张图片，总的数据量就是32*32*3*10000。

此时我们只需要运行以下这段代码（全套运行程序下载链接见文末）：

%% 1.加载数据
load aCIFAR-4D.mat %加载cifar数据
 
%% 2.调用函数进行分类
divideR = [0.9,0.05,0.05];  %训练集/验证集/测试集比例
figflag = 'on';           % 是否画图，'on'为画图，'off'为不画
 
% 指定训练选项
options.solverName = 'sgdm'; %求解器，'sgdm'（默认） | 'rmsprop' | 'adam'
options.MaxEpochs = 100;    %最大迭代次数，默认30
options.InitialLearnRate = 0.03; %初始化学习速率（默认0.005）
options.Plots = 'training-progress'; %是否显示训练过程，'none' 为不显示（默认） | 'training-progress'为显示
options.ValidationFrequency = 10;   %验证频率，即每间隔多少次迭代进行一次验证
options.LearnRateSchedule = 'piecewise'; %是否在一定迭代次数后学习速率下降
options.LearnRateDropFactor = 0.9;  %学习速率下降因子
options.LearnRateDropPeriod = 100;   %学习速率下降时的迭代数
 
% 网络结构设置
conLayer = [5,5,32,1,2;  %波器高为5，宽为5，滤波器数量为32，步长1，填充2
            5,5,128,1,2;  %波器高为5，宽为5，滤波器数量为128，步长1，填充2
            5,5,256,1,2]; %波器高为5，宽为5，滤波器数量为256，步长1，填充2
poolingLayer = {'maxPooling2dLayer',3,3,2,0;   %最大池化层，尺寸为3*3，步长2，填充0
                'maxPooling2dLayer',3,3,2,0;   %最大池化层，尺寸为3*3，步长2，填充0
                'maxPooling2dLayer',3,3,2,0};  %最大池化层，尺寸为3*3，步长2，填充0
fcLayer = []; %不再额外设置全连接层
% 调用函数进行分类
[accuracy,recall,precision,net,info] = FunClassCNNs(dataX,dataY,divideR,conLayer,poolingLayer,fcLayer,options,figflag);

运行程序，可以得到如下结果，这个和MNIST数据集类似，就不展开说了。

对于CIFAR-10数据集的程序运行结果

大致调了调，得到的正确率大概在76%，参照这个CIFAR-10算法正确率排名，这个结果马马虎虎也可以进榜单了。

3.iris鸢尾花数据集

这里介绍一下鸢尾花数据集，鸢尾花在机器学习里是常客之一。数据集由具有150个实例组成，其特征数据包括四个：萼片长、萼片宽、花瓣长、花瓣宽。数据集中一共包括三种鸢尾花，分别叫做Setosa、Versicolor、Virginica，就像下图：

鸢尾花

也就是说这组数据每组的维度是1*4，也就是一维数据，总共有150组数据。

在这个例子里我们还演示了当标签为字符串类型时的处理方法。

此时我们只需要运行以下这段代码（全套运行程序下载链接见文末）：

%% 1.加载数据
load afisheriris.mat %加载fisheriris数据
% 通过以下代码将它们转换为数字 1-3 并赋值给 dataY
species_mapping = containers.Map({'setosa', 'versicolor', 'virginica'}, [1, 2, 3]);
% 使用映射将 species 中的类别名称转换为数字
dataY = cellfun(@(x) species_mapping(x), species);
% 将meas矩阵转换为 4x1x1x150 的四维矩阵
dataX = reshape(meas', [4, 1, 1, 150]);
%% 2.调用函数进行分类
divideR = [0.7,0.15,0.15];  %训练集/验证集/测试集比例
figflag = 'on';           % 是否画图，'on'为画图，'off'为不画
 
% 指定训练选项
options.solverName = 'sgdm'; %求解器，'sgdm'（默认） | 'rmsprop' | 'adam'
options.MaxEpochs = 200;    %最大迭代次数，默认30
options.InitialLearnRate = 0.03; %初始化学习速率（默认0.005）
options.Plots = 'training-progress'; %是否显示训练过程，'none' 为不显示（默认） | 'training-progress'为显示
options.ValidationFrequency = 10;   %验证频率，即每间隔多少次迭代进行一次验证
options.LearnRateSchedule = 'piecewise'; %是否在一定迭代次数后学习速率下降
options.LearnRateDropFactor = 0.9;  %学习速率下降因子
options.LearnRateDropPeriod = 100;   %学习速率下降时的迭代数
options.GradientThreshold = 1;       %梯度极限，默认为Inf
 
% 网络结构设置
conLayer = [2,1,4,1,0]; %波器高为2，宽为1，滤波器数量为4，步长1，填充0
poolingLayer = {'maxPooling2dLayer',2,1,1,0};  %最大池化层，尺寸为2*1，步长1，填充0
fcLayer = [];
% 调用函数进行分类
[accuracy,recall,precision,net,info] = FunClassCNNs(dataX,dataY,divideR,conLayer,poolingLayer,fcLayer,options,figflag);

需要注意此时，设置滤波器的高与宽，方向要与输入数据dataX保持一致。也就是说dataX的维度是4*1*1*150，滤波器就得设置成2*1，而不能是1*2。

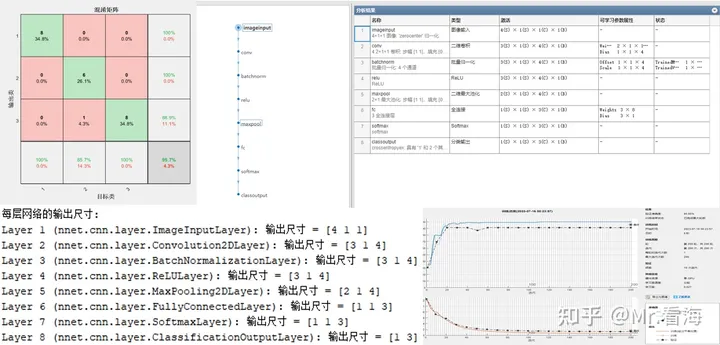
对iris鸢尾花数据集运行结果

这个数据集运行得到的准确率是95.65%。

三、总结

总的来说，自己编程的方法可以快速实现简单的功能，但是用于工程和研究还是欠缺一些必要的图表。

使用封装函数对复杂的CNN训练和评估流程进行了高度封装，大家只需要提供数据和指定参数，就可以轻松进行模型的训练和评估，大大减轻了同学们负担；另外函数接收多个参数作为输入，包括网络结构和训练选项等，使得用户可以根据自己的需求灵活地定制和配置模型，适应各种不同的应用场景；此函数不仅实现了CNN模型的训练，还对模型的性能进行了全面评估，包括准确度等指标，并返回了训练过程中的详细信息，助力用户快速理解模型的性能，并进行后续的优化调整。

需要上述三个案例的代码和封装函数的代码， 可以在下述链接获取：

使用CNN进行模式识别（分类）代码 - 工具箱文档 | 工具箱文档

关于CNN的理论讲解可以看这里：

【深度学习-第2篇】CNN卷积神经网络30分钟入门！足够通俗易懂了吧（图解） - 知乎