使用3DLiDAR传感器进行基于同心区域的区域地面分割和地面似然估计_lidar 地面分割

论文：https://arxiv.org/pdf/2108.05560.pdf

github:https://github.com/LimHyungTae/patchwork

摘要

对于在地面移动平台上导航或邻近目标识别，地面分割是至关重要的。然而，地面并不平坦，存在陡峭的斜坡；崎岖不平的道路；或物体，例如路缘石、花坛等。为了解决该问题，本文提出了一种创新的，称为 Patchwork 的地面分割方法，它对于解决分割不足问题具有鲁棒性，并且工作频率超过 40 Hz。本文中，点云以基于同心区域模型划分，在 bin 之间分配适当的点云，接着执行区域级地平面拟合，估计每个bin的部分地面。最后，引入地面似然估计以显着减少误差。经过在 SemanticKITTI 和崎岖地形数据集上进行的实验验证，我们提出的方法与最先进的方法相比产生了有好的性能，与基于地面平面拟合的方法相比，速度更快。

引言

随着移动平台感知周围环境的需求不断增加，例如无人驾驶地面车辆 (UGV)、无人驾驶飞行器 (UAV) 或自动驾驶汽车。为此，许多研究人员应用了各种 3D 感知方法 [1]-[4]。特别是，3D 光检测和测距 (LiDAR) 传感器已被广泛部署，因为它允许厘米级精度和全向传感，以及与立体相机相比测量远距离的能力。因此，由 LiDAR 传感器捕获的 3D 点云用于语义分割 、跟踪 、检测 等。

在本文中，我们特别关注地面分割任务。地面分割有两个主要目的。一是估计成功导航的可移动区域。本文更加强调的另一个目的是分割点云以识别或跟踪移动对象。地面车辆或人类不可避免地与地面接触；理想情况下，动态对象可以通过简单的方式识别，例如通过欧几里得聚类，如果地面被很好地估计。此外，由于大多数云点属于地面，因此在预处理阶段执行对象分割或检测时，地面分割可以显着降低计算能力。因此，本研究中的地面不仅是指道路这种可移动的区域，还包括移动物体可以接触到的所有区域，包括人行道或草坪。

在这项研究中，如图 1 所示，我们提出了一种新颖的基于同心区域模型 (CZM) 的区域地面分割方法，称为 Patchwork，它是区域地面平面拟合 (R-GPF) 在 我们之前的研究。 在我们之前的研究中，R-GPF 的目的是估计用于静态地图构建的地面点，而在这里，我们只关注 3D 点云上的地面分割。 我们还对 bin 大小的影响进行了详细的实验，这在我们之前的论文中没有涉及。

• 据我们所知，这是第一次尝试分析 bin 大小的影响，当使用 SemanticKITTI 数据集在复杂城市环境中估计地平面。 因此，提出了一种有效的、非均匀的、按区域表示的 3D 点云，称为基于 CZM 的表示，其 bin 大小因每个区域而异。

• 此外，我们利用地面似然估计 (GLE) 在垂直度、高度和平整度方面来确定每个bin是否为地面。

  
  图 1. 我们提出的名为 Patchwork 的方法的概述。 Patchwork 主要由三部分组成：基于同心带模型（CZM）的极坐标网格表示、区域地平面拟合（R-GPF）和地面似然估计（GLE）。

• 我们提出的方法在超过 40 Hz 的频率下显示出比最先进的基于区域拟合的方法更好的性能。 特别是，Patchwork 估计具有最小召回方差的地面点，这表明我们提出的方法克服了复杂城市环境中的细分不足问题。

相关工作

A. 地面分割的难点
有人可能会争辩说，这是一项简单的任务，可以通过基于传感器高度过滤点云或使用 RANSAC（这是一种著名的平面估计方法）来轻松估计。不幸的是，有三个主要问题阻碍了算法进行精确的地面分割：a）存在部分陡峭的斜坡或颠簸的道路，b）路缘石或花坛使某些区域不平坦，以及 c）因为所有周围的物体都被考虑作为地面分割任务中的异常值，这些目标阻碍了平面拟合。由于这些原因，有时会出现欠分割，在这种情况下，属于不同对象的点被合并到同一段中[6]，[12]。

B. 地平面估计方法
为了解决这些问题，许多研究人员研究了各种方法。例如，Douillard 和Chen。 [18] 采用了基于高斯过程的方法。另一方面，Tse，Byun 和 Rummelhard 等人提出了基于马尔可夫随机场的方法。这些方法可用于估计详细的地面点，但需要大量计算时间，因此可能不适合将它们用作速度应保证在 20 Hz 以上的预处理算法。

C. 扫描表示
同时，与基于奇异平面模型的方法相比，基于网格表示的方法已被广泛利用表达性。特别是，目前普遍采用极坐标网格表示来处理柱坐标中的点云，因为它自然地补偿了 3D LiDAR 传感器的几何特征。在实践中，Thrun 等人提出了一种基于网格单元的二元地面分类方法，以概率方式预测 DARPA 挑战中自动驾驶的可移动区域。这些方法主要分为两类：a）基于高程图的方法和b）基于模型拟合的方法。因此，后可以进一步分为两种主要方法：a）基于线拟合的方法和 b）基于平面拟合的方法。

D. 基于高程图的 2.5D 网格表示
首先，基于高程图的方法用于通过将 3D 点云编码为 2.5D 网格表示来区分地面和非地面点 。特伦等人利用相对高度和 Asvadi 等人在每个网格上使用平均高度及其协方差。这些方法在速度和计算成本方面优于其他方法。但是，有时陡坡区域可能会被认为是非地面区域，因为其上、下确界点在 Z 轴上的 z 值差异大。

E. 基于多线拟合的地面分割
接下来，Himmelsbach和 Steinhauser 等人在均匀的极坐标网格表示上引入了 2D 线拟合来估计每个网格上的直线方程。然后，在每个网格中，通过比较常数阈值和估计的参数（例如点到线的距离、梯度或 y 截距）来确定点是否为地面点。

F. 基于多平面拟合的地面分割
其他研究人员分享了他们对区域拟合但提高鲁棒性的看法，他们进行了基于区域平面拟合的方法。例如，Zermas 等人将点云沿车身框架的x轴分为三部分，即车辆的前进方向。该方法基于假设：斜率通常沿 x 轴变化；然而，当涉及到崎岖不平的道路或复杂的十字路口时，这种假设有时会失败。为了解决这个问题，Naksri 等人提出了一种使用扫描数据中的连续环形图案的斜率稳健方法，以及沿径向方向的区域估计平面连续性的概念。此外，Naksri 和程等人提出了一种根据云点密度或入射角设置网格大小的自适应方法。

G. 基于深度学习的方法
当然，随着深度学习时代的到来，Milioto 等人 提出 RangeNet++ 来估计 3D 点云和 Paigwar 等人提出了 GndNet，它以基于网格的表示估计地平面信息，以实时识别地面点。不幸的是，这些方法通常需要大量的计算资源。此外，这些方法往往高度适合训练数据集的环境；因此，当在与训练数据集或不同传感器配置完全不同的环境中使用时，它们的性能可能会降低 。

Patchwork方法

以下段落重点介绍了 Patchwork 每个模块背后的问题定义和推理。 Patchwork 主要由三部分组成：CZM、R-GPF 和 GLE。

A. 问题定义
首先，我们首先将此时的点云表示为P。然后，让 P = { p 1 , p 2 , . . . , p k , . . . , p N } P = \{p_1, p_2, . . . , p_k, . . . , p_N\} P={p1​,p2​,...,pk​,...,pN​} 是一组云点，包含由 3D LiDAR 传感器获取的时刻的 N 个点，其中每个点 $p_k$ 由笛卡尔坐标中的 p k = { x k , y k , z k } p_k = \{x_k, y_k, z_k\} pk​={xk​,yk​,zk​} 组成。 在本文中，P被明确分为两类：一组地面点 $G$ 及其补集 $G_c$，满足 $\hat{G}\cup {\hat{G}}^c=P$。注意 $G_c$ 表示非地面点，包括车辆、墙壁、街道树 、行人等。

接下来，估计的地面点可以定义为 $\hat{G}$ ,由于估计不可避免地包含固有误差，实际上来自非地面物体的一些点可能包含在 G^ 中，反之亦然。 综上所述，$\hat{G}$ 和 ${\hat{G}}_c$ 表示如下：

$$\hat{G}=TP\cup FPand{\hat{G}}^c=FN\cup TN$$
其中$\hat{G}$和 ${\hat{G}}^c$也满足$\hat{G}\cup {\hat{G}}^c=P$，并且 TP、FP、FN 和 TN 分别表示真阳性、假阳性、假阴性和真阴性的集合。 因此，我们的目标是从点云 P 中辨别$\hat{G}$和 ${\hat{G}}^c$，同时估计尽可能少的 FP 和 FN。

B. 同心区模型
如前所述，大多数基于多平面的方法都基于假设：可观测世界可能不是平坦的。因此，地平面估计应该被推倒，通过假设可能的非平坦世界有小块或bins，并且地面在该区域内确实可以是平坦的

因此，以前的一些方法利用统一的极坐标网格表示，或 S，将点云划分为具有规则间隔的径向和方位角方向的多个 bin，即环和扇区 。更具体地说，让 $N_r$和 $N_{\theta }$ 分别是环和扇区的数量。然后，S 被划分为相同大小的扇环bin，其径向大小为 $L_{max}/N_r$，其中 $L_{max}$ 表示最大边界长，扇区方位角大小为 $2\pi /N_{\theta }$，如图 2(a) 所示。

图 2. (a) 均匀极坐标网格描述(b) 我们基于 CZM 的极坐标网格描述 ©范围的累积分布函数 (CDF)，其中超过 90% 的地面点位于20m以内。

不幸的是，如图 2© 所示，为了考虑泛化，在 SemanticKITTI 数据集 [1] 上的整个序列上测量的实验证据表明，大多数地面点都位于靠近传感器框架的位置。即90%以上属于地面的点位于20m以内。
因此，S 有两个限制。首先，随着距离越来越远，点云变得太稀疏而无法找到正确的地平面，我们称之为稀疏问题。一些方法自适应地调整 bin 的大小以应对对数点分布。但是，bin 大小以线性或二次方式增加，因此稀疏问题并未完全解决。另一方面，当靠近原点的 bin 的太小而无法表示 S 中的单位空间时，有时会导致地平面的右法向量估计失败，我们称之为代表性问题。

为了解决这些问题，提出了基于 CZM 的极坐标网格表示，表示为 C，以一种计算不复杂的方式在 bin 之间分配适当的密度。因此，P被分成多个区域，每个区域由不同大小的bin组成，如图2（b）所示。设 $〈N〉=1,2,...,N$，那么我们提出的模型定义如下：

$$C=\bigcup _{m\in <N_Z>}{Z}_m$$
其中 $Z_m$ 表示 C 的第 m 个区域，$N_Z$ 表示区域的数量，本文根据经验将其设置为 4。 令
Z m = { p k ∈ P ∣ L m i n , m ≤ ρ k < L m a x , m } Z_m=\{p_k\in P |L_{min,m}\leq \rho _k < L_{max,m} \} Zm​={pk​∈P∣Lmin,m​≤ρk​<Lmax,m​}
其中 $L_{min,m}$ 和 $L_{max,m}$ 分别表示 $Z_m$ 的最小和最大径向边界； 然后，$Z_m$ 也被划分为 $N_{r,m}\times N_{\theta ,m}$ 个 bin，其中每个区域具有不同的 bin 大小。 因此，每个 bin $S_{i,j,m}$ 定义如下：

其中，${\rho }_k=\sqrt{x_k^2+y_k^2},{\theta }_k=arctan2(y_k,x_k),\Delta L_m=L_{max,m}-L_{min,m},L_{max,m}=L_{min,m+1}m=1,2,3$

注意：$L_{max,4}=L_{max}$，$L_{min,1}=L_{min}$

其中全局最小边界 $L_{min}$用于考虑移动平台或车辆附近的空旷。 实际上，$Z_1$、$Z_2$、$Z_3$ 和 $Z_4$ 分别称为中心区、四分之一区、半区和外区。 因此有
$$L_{min,2}=\frac{7.L_{min}+L_{max}}{8},L_{min,3}=\frac{3.L_{min}+L_{max}}{4},L_{min,4}=\frac{L_{min}+L_{max}}{2}$$

请注意，Z1 和 Z4 中的 bin 大小设置得更大，以解决稀疏性问题和可表示性问题。 因此，与现有的统一表示相比，C 提高了可表达性，从而允许对法线向量进行稳健估计，从而防止分割不足。 此外，它还减少了实际的 bin 数量，例如，从 S 中的 3240 个到 C 中的 504 个，从而能够以超过 40 Hz 的频率运行（参见第 IV.E 节）

C. 区域级地平面拟合
此后，每个 bin 通过 R-GPF 分配估计的部分接地； 然后合并部分地面点。 在本文中，使用主成分分析 (PCA) 而不是使用 RANSAC。 当然，与 PCA 相比，RANSAC 对异常值的敏感性往往较低。 然而，使用 PCA 的速度比使用 RANSAC 快得多，并且表现出可接受的性能； 因此，基于 PCA 的估计更适合作为预处理过程。 此外，实验表明基于 PCA 的方法至少比基于 RANSAC 的方法快两倍（参见第 IV.E 节）。

给定一个bin，令$C\in R^{3\times 3}$为单位空间内云点的协方差矩阵； 三个特征值 ${\lambda }_a$和对应的三个特征向量${\nu }_a$计算如下：
$$C{\nu }_a={\lambda }_a{\nu }_a$$
其中 α = 1、2、3，并假设${\lambda }_1\ge {\lambda }_2\ge {\lambda }_3$。 然后，对应于最小特征值的特征向量，即 $v_3$最有可能表示地平面的法线向量。 因此，设 $n={\nu }_3=[abc{]}^T$ ，平面系数可以计算为 $d=-n^T\bar{p}$，其中$\bar{p}$ 表示单位空间的平均点。

为简单起见，让第 n 个 bin 是所有 bin 上的 Sn，其值等于$N_c={\sum }_{m=1}^{N_z}{N}_{r,m}\times N_{\theta ,m}$。 如果 Sn 的基数足够大，则选择最低高度的点作为初始种子。 事实上，每个bin 子高度最低的点最有可能属于地面。 设̄${\tilde{z}}_{init}$为所选种子点的总$N_{seed}个数的z均值； 然后，初始估计地面点集 ${\hat{G}}_n^0$ 得到如下:
G ^ n 0 = { p k ∈ S n ∣ z ( p k ) < z ˉ i n i t + z s e e d } \hat G^0_n= \{ p_k \in S_n | z(p_k) < \bar z_{init}+z_{seed}\} G^n0​={pk​∈Sn​∣z(pk​)<zˉinit​+zseed​}
其中 z(·) 返回一个点的 z 值，$z_{seed}$ 表示高度边距。

因为我们的方法是迭代的，所以让在第$l$ 次迭代时设置的估计地面点为${\hat{G}}_n^l$，然后得到${\hat{G}}_n^l$的法向量$n_n^l$，平面系数$d_n^l$计算为:$d_n^l=-(n_n^l{)}^T{\bar{p}}_n^l$，其中${\bar{p}}_n^l$表示${\hat{G}}_n^l$的均值点，最后${\hat{G}}_n^{l+1}$公式计算如下：

其中 ${\hat{d}}_k=-(n_n^l{)}^T{p}_k$ 和 Md 表示平面的距离边距。 该过程重复多次。 根据 Zermas 等人的说法， ${\hat{G}}_n={\hat{G}}_n^3$在经验上是本文中每个 Sn 的最终输出。

请注意，原始 R-GPF与我们的主要区别在于，我们涉及使用自适应初始种子选择来防止 R-GPF 收敛到局部最小值。有时，由于多径问题或 LiDAR 信号的反射，会在实际地面下方获取错误的点云，如图 3(a) 所示。观察到这种现象多发生在$Z_1$，因为反射只发生在信号比较强的区域。这些异常值阻碍了 R-GPF 估计正确的地平面。

图 3. (a) 在应用自适应初始种子选择之前和之后 (b) 在帧 435 周围的 SemanticKITTI 数据集 [1] 序列 00 的 R-GPF 上应用自适应初始种子选择以防止错误点（虚线所示）的影响 . 在（a）中，虚线圆圈内的误测点有时被选为初始种子，然后导致区域地平面拟合失败，由蓝色区域表示。 在本文中，绿色、蓝色和红色点分别表示 TPs、FNs 和 FPs。 蓝点越少越好。

为了解决这个问题，我们利用仅在$Z_1$中的地面点的 z 值主要分布在 $-h_s$ 附近的事实，其中 hs 代表传感器高度。因此，当估计 ${\hat{G}}_n^0$ 时，如果 $z_k$ 低于 $M_h\cdot h_s$，则过滤掉属于$Z_1$ 的 $S_n$ 中的 $p_k$，其中 $M_h$ < -1 是高度边际。对于不属于$Z_1$的$S_n$，自适应阈值随着m变大而减小，以避免对可能来自下坡的点进行不当过滤，这些点实际上是TP。

D.地面似然估计
为有必要稳健地辨别${\hat{G}}_n$是否属于实际地面，提出了 GLE，这是一种用于二元分类的区域概率测试。为这样做，Patchwork 利用 GLE 来提高整体精度，不包括由非地面点组成的初始非预期平面。

令 $L(\theta |\chi )$为 GLE，其中 θ 表示 Patchwork 的所有参数，$\chi$ 表示遵循具有密度函数 f 的连续概率分布的随机变量。让我们假设每个 bin 彼此独立。然后，$L(\theta |\chi )$表示为

其中 θn 和 Xn 分别表示每个 ${\hat{G}}_n$ 的参数和随机变量。请注意，下标 n 表示参数来自 ${\hat{G}}_n$。

根据我们的先验知识，每个${\hat{G}}_n$是地面点以垂直度、高程和平面度来定义，分别表示为 $\phi (\cdot )、\psi (\cdot )和\phi (\cdot )$，如下：
$$f(X_n|{\theta }_n)\equiv \phi (v_3,n)\cdot \psi ({\bar{z}}_n,r_n)\cdot \phi (\psi ({\bar{z}}_n,r_n),{\sigma }_n)$$

其中${\bar{z}}_n$, $r_n$, 和 ${\sigma }_n$ 表示平均 z 值，原点之间的距离和 $S_n$ 的质心，以及表面变量，其中 ${\sigma }_n=\frac{{\lambda }_{3,n}}{{\lambda }_{1,n}+{\lambda }_{2,n}+{\lambda }_{3,n}}$。

• Uprightness
  如果 ${\hat{G}}_n$属于实际地面
  （即大部分点都在 TP 中），观察到 $v_{3,n}$ 可能与地面车辆接触的地面正交。换句话说，$v_{3,n}$ 倾向于垂直于传感器框架的 X-Y 平面。因此，提出了垂直度指示函数来利用几何特征作为
  

  其中 z = [0 0 1] 和${\theta }_{\tau }$是直立边距，表示为$v_{3,n}$与 X-Y 平面之间的角度。也就是说，${\theta }_{\tau }$越大，标准就越保守。如图 4(a) 和 (b) 所示，红色区域代表不满足垂直度的情况，因此$\varphi (v_{3,n})$等于 0。通过实验，我们将${\theta }_{\tau }$设置为 45°，根据经验确定它足够严格（参见第 IV.B 节）。

• Elevation
  不幸的是，仅使用 uprightness 无法过滤属于汽车引擎盖或车顶的 ${\hat{G}}_n$。此外，当汽车等大型物体靠近传感器框架时，会发生遮挡，从而产生局部观察问题。也就是说，被遮挡空间上方的部分测量浊点被预测为${\hat{G}}_n$，事实上，这不是空间中的最低部分。这种现象如图4（a）的左侧所示。

  
  图 4.

  • (a) (L-R)：在 SemanticKITTI 数据集上的第 2,810 帧周围的序列 00 应用高程滤波器的前后。 请注意，表示 FP 的红色浊点已被过滤。
  • (b) (L-R)：在第 286 帧周围为序列 10 应用平滑的前后，其中青色点表示通过平滑度恢复的 TP，之前通过高程过滤。 绿色、蓝色和红色区域分别表示满足 GLE、按高程过滤和按平滑过滤的区域。
  • © (T-B)：在 SemanticKITTI 数据集的整个序列上，在中央区 $Z_1$ 和四分之一区 $Z_2$ 和外部区 $Z_4$ 中单独使用垂直度，两个相应的部分地面估计${\hat{G}}_n$之间的平均 z 值的概率分布函数 (PDF)。 虚线表示传感器的地面高程

  为了解决这个问题，提出了一个条件逻辑函数 $\psi ({\hat{z}}_n,r_n)$。高程过滤器的关键思想是由 Asvadi 等人提出的。 [9]：一旦传感器框架附近的 ${\hat{z}}_n$ 与 $-h_s$ 相比相当高，${\hat{G}}_n$可能不是地面。

  实验证据支持我们的理论，如图 4（c）所示。仅使用直立性，$T{P}_s$ 和 $F{P}_s$ 基于 ${\hat{z}}_n$ 变得可区分，当 $r_n$ 很小时，$T{P}_s$的损失很小，即${\hat{G}}_n$在 $Z_1$ 和 $Z_2$ 中的情况。相反，当 rn 很大时，$T{P}_s$ 和 $F{P}_s$ 是无法区分的，即 ${\hat{G}}_n$在 $Z_4$ 中。

  基于这些观察， $\psi ({\hat{z}}_n,r_n)$定义如下：
  

  其中 $\kappa (\cdot )$ 表示根据 $r_n$ 呈指数增长的自适应中点函数。如图 4(a) 所示，如果 ${\bar{z}}_n$ 低于 $\kappa (r)$，则当$r_n$ 小于恒定范围参数$L_\tau $时，$ψ(\hat z_n, r_n)$ 的值高于 0.5。请注意，当 $r_n$ 超过$L_\tau $时，$ψ(\hat z_n, r_n)$ 总是变为 1，因为随着 rn 变大，不清楚 G ^n 是来自非地面物体还是来自陡峭的斜坡。

• Flatness
  最后，平坦度的目的是还原一些通过高程过滤的 $F{N}_s$，如果它们绝对是一个偶数平面。例如，如果${\hat{G}}_n$ 属于一个非常陡峭的上坡，因此如果${\hat{z}}_n$ 大于$\kappa (r)$，则 ${\hat{G}}_n$有时会通过 $\psi ({\hat{z}}_n,r_n)$过滤掉。为了解决这个问题，我们利用表面变量${\sigma }_n$来检查被认为是 $F{N}_s$ 的 ${\hat{G}}_n$ 的平坦度，即使$\psi ({\hat{z}}_n,r_n)$低于 0.5。为此， $\phi (\psi ({\hat{z}}_n,r_n),{\sigma }_n)$的可定义为
  

  其中 $\zeta >1$ 和 ${\sigma }_{\tau ,m}$ 分别表示增益的大小和取决于 $Z_m$ 的表面变量的阈值。通过这样做，陡峭上坡的 GLE 增加，尽管${\hat{z}}_n$高于 $\kappa (r_n)$，但它们可以恢复为地面估计。

  因此，最终估计的地面点可以直接表示为：
  
  其中 [·] 表示 Iverson 括号，如果条件满足则返回 true，否则返回 false。

IV.实验

A Dataset

• SemanticKITTI 数据集
  为了评估我们提出的方法相对于其他地面分割算法的地面分割性能，我们对 SemanticKITTI 数据集进行了实验。因此，用所选类别注释的点，即车道标记、道路、停车场、人行道、其他地面、植被和地形，被认为是要提取的真实地面点。请注意，植被包含树叶，因此只有相对于传感器框架的 z 值低于 -1.3 m 的点才被认为是地面实况。
• Rough Terrain Dataset
  尽管 SemanticKITTI 数据集代表了各种城市环境，但数据仅从人行道上的车辆平台获取。因此，我们进行了一个额外的、更具挑战性的实验来证明我们提出的算法的鲁棒性和通用性。如图 5 所示，我们的机器人平台配备了 3D LiDAR (Ouster OS0-128)。这些数据是从韩国大田 KAIST 校园的崎岖地形环境中获取的。

图 5.（L-R）我们的机器人平台进行额外的实验。 KAIST 校园内的崎岖地形环境。

• B. Error Metrics
  为了定量评估我们提出的方法，我们考虑了精度、召回率、F1 分数和准确度。 令$N_{TP}、N_{TN}、N_{FP}、N_{FN}$$分别为TP、TN、FP、FN中的点数； 那么这些指标定义如下：
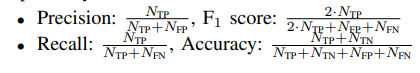  C. Parameters of Patchwork
  我们设置 { N r , 1 , N r , 2 , N r , 3 , N r , 4 = { 2 , 4 , 4 , 4 } \{N_{r,1},N_{r,2},N_{r,3},N_{r,4}=\{2, 4, 4, 4\} {Nr,1​,Nr,2​,Nr,3​,Nr,4​={2,4,4,4}, { N θ , 1 , N θ , 2 , N r θ , 3 , N θ , 4 = { 16 , 32 , 54 , 32 } \{N_{θ,1}, N_{θ,2}, N_{rθ,3}, N_{θ,4} = \{16 , 32, 54, 32\} {Nθ,1​,Nθ,2​,Nrθ,3​,Nθ,4​={16,32,54,32}, $L_{min}$ = 2.7m, $L_{max}$ = 80.0m 对于 CZM。 对于 R-GPF，$N_{seed}$ = 20，$z_{seed}$ = 0.5，$M_d$ = 0.15 和 $M_h$ = -1.1。 $z_{seed}$ 和 $M_d$ 越小，标准就越保守。 最后，对于 GLE，$L_{\tau }$ = $L_{max,2}$,${\sigma }_{\tau ,1}$ = 0.00012 和 ${\sigma }_{\tau ,2}$= 0.0002，其中${\sigma }_{\tau }$低于 0.01 的云点被认为是一个平面，但我们设置了更严格的标准

V、结果与讨论

A. Performance Analysis with Different Bin Sizes

首先分析 bin 大小的影响，这在我们之前的研究中没有进行。如图 6 所示，较大的 bin 大小会导致精度大幅提高，而召回率下降很小；因此，它显着提高了 $F_1$ 分数。这个结果意味着 bin 区域越大，可以更好估计地面。然而，由于每个 bin 的分辨率降低，随着 bin 大小变大，它会导致更低的召回率。

图 6. 在 SemanticKITTI 数据集上，随着 bin 大小$(N_r,N_{\theta })$ 和垂直度阈值 ${\theta }_{\tau }$ 的变化，uniform polar表示的性能变化。

B. Impact of Uprightness
不幸的是，bin 大小的大幅扩大并不能解决精度的大方差，如图 6 所示。然而，仅使用 uprightness 会导致精度的显着性能提高，同时减少方差，从而提高$F_1$ 分数。因此，结果表明我们的uprightness成功地过滤掉了错误估计的部分地面。然而，较高的 ${\theta }_{\tau }$ 允许实际的$T{P}_s$，例如陡坡区域或道路和路缘之间的边界区域，被归类为非地面，因此召回率略有下降。因此，我们可以得出结论，45°的 ${\theta }_{\tau }$在整个实验过程中产生了最合理的估计。
C. Effectiveness of Ground Likelihood Estimation
此后，验证了 GLE 的有效性。如图 7、图 8 和表1 所示，我们的基线算法 R-GPF 估计具有许多 FP 的地平面，因为 RGPF 优先考虑最大化召回率。同时，我们的 GLE 成功过滤掉了错误估计的部分地面，从而显着减少了 FN。特别是，验证了许多墙壁和停放的汽车可以分别被垂直度和高度过滤器拒绝。

图 7. (L) R-GPF 的地面估计结果和 ® SemanticKITTI 数据集上第 429 帧周围序列 00 的 Patchwork。 我们提出的 GLE 成功拒绝了 $F{P}_s$，绿色、蓝色和红色点分别表示 $T{P}_s$、$F{N}_s$ 和$F{P}_s$。 红点越少越好
图 8. 基于多平面拟合的方法的定性比较。 （L-R，T-B）：GPF、CascadedSeg、R-GPF和 Patchwork 在崎岖地形上的输出。 即使地面颠簸和倾斜，我们的方法也显示出它的鲁棒性。 黄色和青色点分别表示估计的地面和非地面。 蓝色圆圈内的点表示 FNs，红色圆圈内的点表示 FPs

D. 与最先进方法的比较
Patchwork 与最先进的方法进行了定量比较，即 RANSAC、LineFit1、GPF2和 CascadedSeg3。我们利用开源实现进行实验。

如图 9 所示，其他方法显示了详细的地面估计。然而，他们在非平面区域遇到困难，包括陡坡、复杂的交叉路口以及存在许多路缘石的区域。特别是，LineFit 在遇到起伏地形或灌木丛区域时可能很敏感，估计许多 FNs。另一方面，GPF 和 CascadeSeg 中的一些 bin 有时会趋向于收敛到局部最小值，因为 bin 大小太大，因此假设 bin 内的地面是平面的并不安全；尤其是在崎岖不平的地形上，这种现象更加严重，如图 8 所示。因此，它们在 SemanticKITTI 数据集上显示出很大的召回方差，如表1所示。

图 9. 在 Semantic KITTI 数据集 (T-B) 上，所提出的方法和最先进的方法产生的地面估计结果比较：第 00 帧围绕第 429 帧和第 1,800 帧，06 围绕第 505 帧，01 围绕第 180 帧 . 绿色、蓝色和红色的点分别表示 TPs、FNs 和 FPs。 蓝点和红点越少越好，绿点越多越好

表 I：在 SemanticKITTI 数据集的整个序列上与最先进方法的性能比较。 U、E 和 F 分别表示垂直度、高度和平面度； 红色表示低精度/召回率和大标准偏差

相比之下，我们提出的方法显示出有希望的性能。特别是，我们的方法估计地面相对于其他方法几乎没有召回差异。这证实了我们的方法克服了分割不足的问题，因此对城市环境中的这些极端情况具有鲁棒性。

同时，从图 9 可以看出，Patchwork 的 FN 数量比 LinFit、GPF 和 CascadedSeg 的数量要多，但实际上这些是某些对象的最低部分，如图 7 所示。这意味着即使 尽管 FN 降低了定量指标的性能，但它们更有助于解决细分不足的问题
E. Algorithm speed
为了检查每种算法的速度，我们使用了 Intel® Core™ i7-7700K CPU。请注意，我们提出的方法显示了各种基于多平面拟合的方法中最快的速度，如表2所示。特别是，令人惊讶的是，Patchwork 比 R-GPF 更快。这是因为我们的CZM减少了bin的数量，所以平面拟合的量也减少了；例如，Patchwork 使用 504 个 bin，而 R-GPF 使用 3,240 个 bin。此外，我们的方法基于 PCA，因此它也比 CascadedSeg 更快，CascadedSeg 是一种基于 RANSAC 的方法。因此，该结果表明我们的方法不仅稳健，而且速度足够快，可用于预处理。

表二：SemanticKITTI 数据集序列 05 上多种基于网格的方法的平均算法速度。

六、结论

在这项研究中，提出了一种快速且鲁棒的地面分割方法 Patchwork。与以前的方法相比，我们提出的方法被证明可以克服分割不足的问题。特别是，我们的方法提供了一个分割良好的地面估计，其性能变化较小，这使得移动机器人能够以稳健的方式检测非地面物体。在未来的工作中，我们计划将我们的 Patchwork 应用于运动物体的检测，或者设计一种深度学习辅助的地面似然估计来进行更复杂的地面分割。