不正经

这个屌丝很懒，什么也没留下！

热门标签

tsp java_蚁群算法java实现以及TSP问题蚁群算法求解

作者：不正经 | 2024-06-02 16:36:48

踩

tsp服务是什么跟java

1. 蚁群算法简介

蚁群算法(Ant Clony Optimization， ACO)是一种群智能算法，它是由一群无智能或有轻微智能的个体(Agent)通过相互协作而表现出智能行为，从而为求解复杂问题提供了一个新的可能性。蚁群算法最早是由意大利学者Colorni A., Dorigo M. 等于1991年提出。经过20多年的发展，蚁群算法在理论以及应用研究上已经得到巨大的进步。

蚁群算法是一种仿生学算法，是由自然界中蚂蚁觅食的行为而启发的。在自然界中，蚂蚁觅食过程中，蚁群总能够按照寻找到一条从蚁巢和食物源的最优路径。图(1)显示了这样一个觅食的过程。

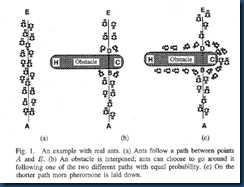
图(1)蚂蚁觅食

在图1(a)中，有一群蚂蚁，假如A是蚁巢，E是食物源(反之亦然)。这群蚂蚁将沿着蚁巢和食物源之间的直线路径行驶。假如在A和E之间突然出现了一个障碍物(图1(b))，那么，在B点(或D点)的蚂蚁将要做出决策，到底是向左行驶还是向右行驶？由于一开始路上没有前面蚂蚁留下的信息素(pheromone)，蚂蚁朝着两个方向行进的概率是相等的。但是当有蚂蚁走过时，它将会在它行进的路上释放出信息素，并且这种信息素会议一定的速率散发掉。信息素是蚂蚁之间交流的工具之一。它后面的蚂蚁通过路上信息素的浓度，做出决策，往左还是往右。很明显，沿着短边的的路径上信息素将会越来越浓(图1(c))，从而吸引了越来越多的蚂蚁沿着这条路径行驶。

2. TSP问题描述

蚁群算法最早用来求解TSP问题，并且表现出了很大的优越性，因为它分布式特性，鲁棒性强并且容易与其它算法结合，但是同时也存在这收敛速度慢，容易陷入局部最优(local optimal)等缺点。

TSP问题(Travel Salesperson Problem，即旅行商问题或者称为中国邮递员问题)，是一种，是一种NP-hard问题，此类问题用一般的算法是很大得到最优解的，所以一般需要借助一些启发式算法求解，例如遗传算法(GA)，蚁群算法(ACO)，微粒群算法(PSO)等等。

TSP问题可以分为两类，一类是对称TSP问题(Symmetric TSP)，另一类是非对称问题(Asymmetric TSP)。所有的TSP问题都可以用一个图(Graph)来描述：

令

$V=\{c_1,c_2,\ldots,c_i,\ldots,c_n\},i=1,2,\ldots,n$是所有城市的集合.$c_i$表示第i个城市， $n$为城市的数目；

$E=\{(r,s):r,s \in V\}$是所有城市之间连接的集合；

$C=\{c_{rs}:r,s \in V\}$是所有城市之间连接的成本度量(一般为城市之间的距离)；

如果$c_{rs} = c_{sr}$, 那么该TSP问题为对称的，否则为非对称的。

一个TSP问题可以表达为：

求解遍历图$G=(V,E,C)$，所有的节点一次并且回到起始节点，使得连接这些节点的路径成本最低。

3. 蚁群算法原理

假如蚁群中所有蚂蚁的数量为m，所有城市之间的信息素用矩阵pheromone表示，最短路径为bestLength，最佳路径为bestTour。每只蚂蚁都有自己的内存，内存中用一个禁忌表(Tabu)来存储该蚂蚁已经访问过的城市，表示其在以后的搜索中将不能访问这些城市；还有用另外一个允许访问的城市表(Allowed)来存储它还可以访问的城市；另外还用一个矩阵(Delta)来存储它在一个循环(或者迭代)中给所经过的路径释放的信息素；还有另外一些数据，例如一些控制参数$(\alpha，\beta，\rho，Q)$，该蚂蚁行走玩全程的总成本或距离(tourLength)，等等。假定算法总共运行MAX_GEN次，运行时间为t。

蚁群算法计算过程如下：

(1)初始化

设t=0，初始化bestLength为一个非常大的数(正无穷)，bestTour为空。初始化所有的蚂蚁的Delt矩阵所有元素初始化为0，Tabu表清空，Allowed表中加入所有的城市节点。随机选择它们的起始位置(也可以人工指定)。在Tabu中加入起始节点，Allowed中去掉该起始节点。

(2)为每只蚂蚁选择下一个节点。

为每只蚂蚁选择下一个节点，该节点只能从Allowed中以某种概率(公式1)搜索到，每搜到一个，就将该节点加入到Tabu中，并且从Allowed中删除该节点。该过程重复n-1次，直到所有的城市都遍历过一次。遍历完所有节点后，将起始节点加入到Tabu中。此时Tabu表元素数量为n+1(n为城市数量)，Allowed元素数量为0。接下来按照(公式2)计算每个蚂蚁的Delta矩阵值。最后计算最佳路径，比较每个蚂蚁的路径成本，然后和bestLength比较，若它的路径成本比bestLength小，则将该值赋予bestLength，并且将其Tabu赋予BestTour。

$gif.latex?p_%7Bij%7D%5Ek%28t%29%20%3D%20%5Cleft%5C%7B%5Cbegin%7Bmatrix%7D%5Cfrac%20%7B%5B%5Ctau_%7Bij%7D%28t%29%5D%5E%7B%5Calpha%7D%20%5B%5Ceta_%7Bij%7D%5D%5E%7B%5Cbeta%7D%7D%20%7B%5Csum_%7Bk%20%5Cin%20allowed_k%7D%5B%5Ctau_%7Bij%7D%28t%29%5D%5E%7B%5Calpha%7D%20%5B%5Ceta_%7Bij%7D%5D%5E%7B%5Cbeta%7D%20%7D%20%26%20if%20if%20j%20%5Cin%20allowed_k%20%5C%5C%200%20%26%20otherwise%20%5Cend%7Bmatrix%7D%20%5Cright$

(公式1)

$gif.latex?Delta%20%5Ctau_%7Bij%7D%5Ek%20%3D%20%5Cleft%5C%7B%5Cbegin%7Bmatrix%7D%20%5Cfrac%7BQ%7D%7BL_k%20%7D%20%26%20if%20k_%7Bth%7D%20ant%20uses%20edge%20%28i%2Cj%29%20in%20its%20tour%20between%20t%20and%20%28t+n%29%20%5C%5C%200%26%20otherwise%20%5Cend%7Bmatrix%7D%5Cright.$

(公式2)

其中$p_{ij}^{(t)}$表示选择城市j的概率，$k$表示第$k$个蚂蚁，$\tau_{ij}^{(t)}$表示城市$i,j$在第$t$时刻的信息素浓度，$\eta_{ij}$表示从城市i到城市j的可见度，

$\eta_{ij} = \frac 1 {d_{ij}}$，$d_{ij}$表示城市$i,j$之间的成本(或距离)。由此可见$d_{ij}$越小，$\eta_{ij}$越大，也就是从城市$i$到$j$的可见性就越大。$\Delta \tau_{ij}^k$表示蚂蚁$k$在城市$i$与$j$之间留下的信息素。

$L_k$表示蚂蚁$k$经过一个循环(或迭代)锁经过路径的总成本(或距离)，即tourLength.$\alpha, \beta, Q$ 均为控制参数。

(3)更新信息素矩阵

令$t=t+n$t，按照(公式3)更新信息素矩阵phermone。

τ_{i j} (t + n) = ρ \cdot τ_{i j} (t) + Δ τ_{i j}

$\tau_{ij}(t+n) = \rho \cdot \tau_{ij}(t) + \Delta \tau_{ij}$

(公式3)

$\tau_{ij}(t+n)$为$t+n$时刻城市$i$与$j$之间的信息素浓度。$\rho$为控制参数，$Delta_ij$为城市$i$与$j$之间信息素经过一个迭代后的增量。并且有

Δ τ_{i j} = \sum_{k = 1}^{m} Δ τ_{i j}^{k}

$\Delta \tau_{ij} = \sum_{k=1}^m \Delta \tau_{ij}^k$

(公式4)

其中$\Delta \tau_{ij}^k$由公式计算得到。

(4)检查终止条件

如果达到最大代数MAX_GEN，算法终止，转到第(5)步；否则，重新初始化所有的蚂蚁的Delt矩阵所有元素初始化为0，Tabu表清空，Allowed表中加入所有的城市节点。随机选择它们的起始位置(也可以人工指定)。在Tabu中加入起始节点，Allowed中去掉该起始节点，重复执行(2)，(3),(4)步。

(5)输出最优值

4. Java实现

在该java实现中我们选择使用tsplib上的数据att48，这是一个对称tsp问题，城市规模为48，其最优值为10628.其距离计算方法如图(2)所示：

图(2)att48距离计算方法

实现中，使用了两个java类，一个Ant类，一个ACO类。

具体实现代码如下(此代码借鉴了蚁群优化算法的JAVA实现)：

Ant类：

1: import java.util.Random;

2: import java.util.Vector;

4: /**

5: *

6: * @author BIAO YU

7: *

8: */

9: public class Ant implements Cloneable {

10:

11: private Vector tabu; //禁忌表

12: private Vector allowedCities; //允许搜索的城市

13: private float[][] delta; //信息数变化矩阵

14: private int[][] distance; //距离矩阵

15:

16: private float alpha;

17: private float beta;

18:

19: private int tourLength; //路径长度

20: private int cityNum; //城市数量

21:

22: private int firstCity; //起始城市

23: private int currentCity; //当前城市

24:

25: public Ant(){

26: cityNum = 30;

27: tourLength = 0;

28:

29: }

30:

31: /**

32: * Constructor of Ant

33: * @param num 蚂蚁数量

34: */

35: public Ant(int num){

36: cityNum = num;

37: tourLength = 0;

38:

39: }

40:

41: /**

42: * 初始化蚂蚁，随机选择起始位置

43: * @param distance 距离矩阵

44: * @param a alpha

45: * @param b beta

46: */

47: public void init(int[][] distance, float a, float b){

48: alpha = a;

49: beta = b;

50: allowedCities = new Vector();

51: tabu = new Vector();

52: this.distance = distance;

53: delta = new float[cityNum][cityNum];

54: for (int i = 0; i < cityNum; i++) {

55: Integer integer = new Integer(i);

56: allowedCities.add(integer);

57: for (int j = 0; j < cityNum; j++) {

58: delta[i][j] = 0.f;

59: }

60: }

61:

62: Random random = new Random(System.currentTimeMillis());

63: firstCity = random.nextInt(cityNum);

64: for (Integer i:allowedCities) {

65: if (i.intValue() == firstCity) {

66: allowedCities.remove(i);

67: break;

68: }

69: }

70:

71: tabu.add(Integer.valueOf(firstCity));

72: currentCity = firstCity;

73: }

74:

75: /**

76: * 选择下一个城市

77: * @param pheromone 信息素矩阵

78: */

79: public void selectNextCity(float[][] pheromone){

80: float[] p = new float[cityNum];

81: float sum = 0.0f;

82: //计算分母部分

83: for (Integer i:allowedCities) {

84: sum += Math.pow(pheromone[currentCity][i.intValue()], alpha)*Math.pow(1.0/distance[currentCity][i.intValue()], beta);

85: }

86: //计算概率矩阵

87: for (int i = 0; i < cityNum; i++) {

88: boolean flag = false;

89: for (Integer j:allowedCities) {

90:

91: if (i == j.intValue()) {

92: p[i] = (float) (Math.pow(pheromone[currentCity][i], alpha)*Math.pow(1.0/distance[currentCity][i], beta))/sum;

93: flag = true;

94: break;

95: }

96: }

97:

98: if (flag == false) {

99: p[i] = 0.f;

100: }

101: }

102:

103: //轮盘赌选择下一个城市

104: Random random = new Random(System.currentTimeMillis());

105: float sleectP = random.nextFloat();

106: int selectCity = 0;

107: float sum1 = 0.f;

108: for (int i = 0; i < cityNum; i++) {

109: sum1 += p[i];

110: if (sum1 >= sleectP) {

111: selectCity = i;

112: break;

113: }

114: }

115:

116: //从允许选择的城市中去除select city

117: for (Integer i:allowedCities) {

118: if (i.intValue() == selectCity) {

119: allowedCities.remove(i);

120: break;

121: }

122: }

123: //在禁忌表中添加select city

124: tabu.add(Integer.valueOf(selectCity));

125: //将当前城市改为选择的城市

126: currentCity = selectCity;

127:

128: }

129:

130: /**

131: * 计算路径长度

132: * @return 路径长度

133: */

134: private int calculateTourLength(){

135: int len = 0;

136: for (int i = 0; i < cityNum; i++) {

137: len += distance[this.tabu.get(i).intValue()][this.tabu.get(i+1).intValue()];

138: }

139: return len;

140: }

141:

142:

143:

144: public Vector getAllowedCities() {

145: return allowedCities;

146: }

147:

148: public void setAllowedCities(Vector allowedCities) {

149: this.allowedCities = allowedCities;

150: }

151:

152: public int getTourLength() {

153: tourLength = calculateTourLength();

154: return tourLength;

155: }

156: public void setTourLength(int tourLength) {

157: this.tourLength = tourLength;

158: }

159: public int getCityNum() {

160: return cityNum;

161: }

162: public void setCityNum(int cityNum) {

163: this.cityNum = cityNum;

164: }

165:

166: public Vector getTabu() {

167: return tabu;

168: }

169:

170: public void setTabu(Vector tabu) {

171: this.tabu = tabu;

172: }

173:

174: public float[][] getDelta() {

175: return delta;

176: }

177:

178: public void setDelta(float[][] delta) {

179: this.delta = delta;

180: }

181:

182: public int getFirstCity() {

183: return firstCity;

184: }

185:

186: public void setFirstCity(int firstCity) {

187: this.firstCity = firstCity;

188: }

189:

190: }

191:

ACO类：

1: import java.io.BufferedReader;

2: import java.io.FileInputStream;

3: import java.io.IOException;

4: import java.io.InputStreamReader;

6: /**

7: *

8: * @author BIAO YU

9: *

10: *

11: */

12: public class ACO {

13:

14: private Ant[] ants; //蚂蚁

15: private int antNum; //蚂蚁数量

16: private int cityNum; //城市数量

17: private int MAX_GEN; //运行代数

18: private float[][] pheromone; //信息素矩阵

19: private int[][] distance; //距离矩阵

20: private int bestLength; //最佳长度

21: private int[] bestTour; //最佳路径

22:

23: //三个参数

24: private float alpha;

25: private float beta;

26: private float rho;

27:

28:

29: public ACO(){

30:

31: }

32: /** constructor of ACO

33: * @param n 城市数量

34: * @param m 蚂蚁数量

35: * @param g 运行代数

36: * @param a alpha

37: * @param b beta

38: * @param r rho

39: *

40: **/

41: public ACO(int n, int m, int g, float a, float b, float r) {

42: cityNum = n;

43: antNum = m;

44: ants = new Ant[antNum];

45: MAX_GEN = g;

46: alpha = a;

47: beta = b;

48: rho = r;

49:

50: }

51:

52: @SuppressWarnings("resource")

53: /**

54: * 初始化ACO算法类

55: * @param filename 数据文件名，该文件存储所有城市节点坐标数据

56: * @throws IOException

57: */

58: private void init(String filename) throws IOException{

59: //读取数据

60: int[] x;

61: int[] y;

62: String strbuff;

63: BufferedReader data = new BufferedReader(new InputStreamReader(new FileInputStream(filename)));

64:

65: distance = new int[cityNum][cityNum];

66: x = new int[cityNum];

67: y = new int[cityNum];

68: for (int i = 0; i < cityNum; i++) {

69: strbuff = data.readLine();

70: String[] strcol = strbuff.split("");

71: x[i] = Integer.valueOf(strcol[1]);

72: y[i] = Integer.valueOf(strcol[2]);

73: }

74: //计算距离矩阵，针对具体问题，距离计算方法也不一样，此处用的是att48作为案例，它有48个城市，距离计算方法为伪欧氏距离，最优值为10628

75: for (int i = 0; i < cityNum - 1; i++) {

76: distance[i][i] = 0; //对角线为0

77: for (int j = i + 1; j < cityNum; j++) {

78: double rij = Math.sqrt(((x[i] - x[j]) * (x[i] - x[j])+ (y[i] - y[j]) * (y[i] - y[j]))/10.0);

79: int tij = (int) Math.round(rij);

80: if (tij < rij) {

81: distance[i][j] = tij + 1;

82: distance[j][i] = distance[i][j];

83: }else {

84: distance[i][j] = tij;

85: distance[j][i] = distance[i][j];

86: }

87: }

88: }

89: distance[cityNum - 1][cityNum - 1] = 0;

90:

91: //初始化信息素矩阵

92: pheromone=new float[cityNum][cityNum];

93: for(int i=0;i

94: {

95: for(int j=0;j

96: pheromone[i][j]=0.1f; //初始化为0.1

97: }

98: }

99: bestLength=Integer.MAX_VALUE;

100: bestTour=new int[cityNum+1];

101: //随机放置蚂蚁

102: for(int i=0;i

103: ants[i]=new Ant(cityNum);

104: ants[i].init(distance, alpha, beta);

105: }

106: }

107:

108: public void solve(){

109:

110: for (int g = 0; g < MAX_GEN; g++) {

111: for (int i = 0; i < antNum; i++) {

112: for (int j = 1; j < cityNum; j++) {

113: ants[i].selectNextCity(pheromone);

114: }

115: ants[i].getTabu().add(ants[i].getFirstCity());

116: if (ants[i].getTourLength() < bestLength) {

117: bestLength = ants[i].getTourLength();

118: for (int k = 0; k < cityNum + 1; k++) {

119: bestTour[k] = ants[i].getTabu().get(k).intValue();

120: }

121: }

122: for (int j = 0; j < cityNum; j++) {

123: ants[i].getDelta()[ants[i].getTabu().get(j).intValue()][ants[i].getTabu().get(j+1).intValue()] = (float) (1./ants[i].getTourLength());

124: ants[i].getDelta()[ants[i].getTabu().get(j+1).intValue()][ants[i].getTabu().get(j).intValue()] = (float) (1./ants[i].getTourLength());

125: }

126: }

127:

128: //更新信息素

129: updatePheromone();

130:

131: //重新初始化蚂蚁

132: for(int i=0;i

133:

134: ants[i].init(distance, alpha, beta);

135: }

136: }

137:

138: //打印最佳结果

139: printOptimal();

140: }

141:

142: //更新信息素

143: private void updatePheromone(){

144: //信息素挥发

145: for(int i=0;i

146: for(int j=0;j

147: pheromone[i][j]=pheromone[i][j]*(1-rho);

148: //信息素更新

149: for(int i=0;i

150: for(int j=0;j

151: for (int k = 0; k < antNum; k++) {

152: pheromone[i][j] += ants[k].getDelta()[i][j];

153: }

154: }

155: }

156: }

157:

158: private void printOptimal(){

159: System.out.println("The optimal length is:" + bestLength);

160: System.out.println("The optimal tour is:");

161: for (int i = 0; i < cityNum + 1; i++) {

162: System.out.println(bestTour[i]);

163: }

164: }

165:

166: public Ant[] getAnts() {

167: return ants;

168: }

169:

170: public void setAnts(Ant[] ants) {

171: this.ants = ants;

172: }

173:

174: public int getAntNum() {

175: return antNum;

176: }

177:

178: public void setAntNum(int m) {

179: this.antNum = m;

180: }

181:

182: public int getCityNum() {

183: return cityNum;

184: }

185:

186: public void setCityNum(int cityNum) {

187: this.cityNum = cityNum;

188: }

189:

190: public int getMAX_GEN() {

191: return MAX_GEN;

192: }

193:

194: public void setMAX_GEN(int mAX_GEN) {

195: MAX_GEN = mAX_GEN;

196: }

197:

198: public float[][] getPheromone() {

199: return pheromone;

200: }

201:

202: public void setPheromone(float[][] pheromone) {

203: this.pheromone = pheromone;

204: }

205:

206: public int[][] getDistance() {

207: return distance;

208: }

209:

210: public void setDistance(int[][] distance) {

211: this.distance = distance;

212: }

213:

214: public int getBestLength() {

215: return bestLength;

216: }

217:

218: public void setBestLength(int bestLength) {

219: this.bestLength = bestLength;

220: }

221:

222: public int[] getBestTour() {

223: return bestTour;

224: }

225:

226: public void setBestTour(int[] bestTour) {

227: this.bestTour = bestTour;

228: }

229:

230: public float getAlpha() {

231: return alpha;

232: }

233:

234: public void setAlpha(float alpha) {

235: this.alpha = alpha;

236: }

237:

238: public float getBeta() {

239: return beta;

240: }

241:

242: public void setBeta(float beta) {

243: this.beta = beta;

244: }

245:

246: public float getRho() {

247: return rho;

248: }

249:

250: public void setRho(float rho) {

251: this.rho = rho;

252: }

253:

254:

255: /**

256: * @param args

257: * @throws IOException

258: */

259: public static void main(String[] args) throws IOException {

260: ACO aco = new ACO(48, 100, 1000, 1.f, 5.f, 0.5f);

261: aco.init("c://data.txt");

262: aco.solve();

263: }

264:

265: }

266:

5. 总结

蚁群算法和其它的启发式算法一样，在很多场合都得到了应用，并且取得了很好的结果。但是同样存在着很多的缺点，例如收敛速度慢，容易陷入局部最优，等等。对于这些问题，还需要进一步的研究和探索，另外蚁群算法的数学机理至今还没有得到科学的解释，这也是当前研究的热点和急需解决的问题之一。注：TSP数据文件以及两篇早期的关于蚁群算法的文章包含在附件中，请点击此处下载附件。

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/不正经/article/detail/663453