信号初级谐波_偶次谐波

谐波的英文为：harmonic

周期量的傅里叶级数式中阶次大于1的分量。
根据傅立叶等人提出的谐波分析方法——傅里叶变换，满足Dirichlet条件的、以T为周期的周期函数f(t)，在连续点处，可以展开为常数与一组具有共同周期的正弦函数和余弦函数之和。
谐波的频率等于基波的频率的整数倍，基波频率3倍的波称之为三次谐波，基波频率5倍的波称之为五次谐波，以此类推。不管几次谐波，他们都是正弦波。
采用傅里叶变换，方波可以分解为基波和3、5、7、11、13……次谐波的组合，n次谐波含量是基波的1/n。
当电网中的电压或电流波形非理想的正弦波时，即说明其中含有频率高于50Hz的电压或电流成分，我们将频率高于50Hz的电流或电压成分称之为谐波。
当谐波频率为工频频率的整数倍时，我们将其称之为整数次谐波，这类谐波通常用次数来表示。例如：将频率为工频频率5倍（250Hz）的谐波称之为5次谐波，将频率为工频频率7倍（350Hz）的谐波称之为7次谐波，依此类推。
当谐波频率不是工频频率的整数倍时，我们将其称之为分数谐波。这类谐波通常直接使用谐波频率来表示。例如：频率为1627Hz的谐波。
下图形象的再现了通过基波、3、5、7次谐波合成近似方波的过程。

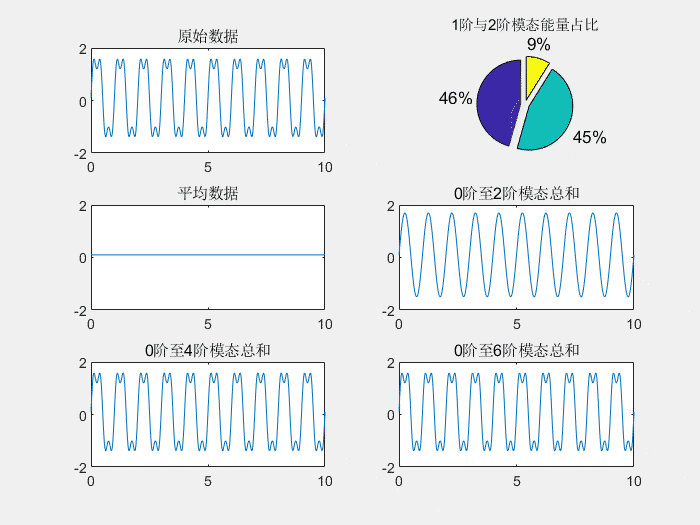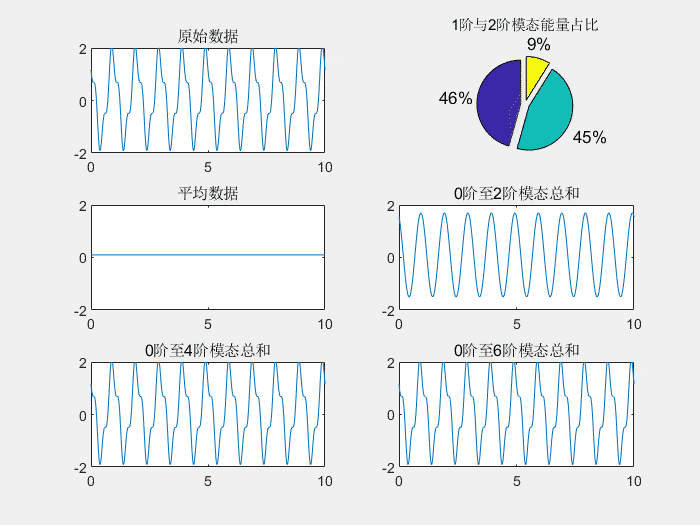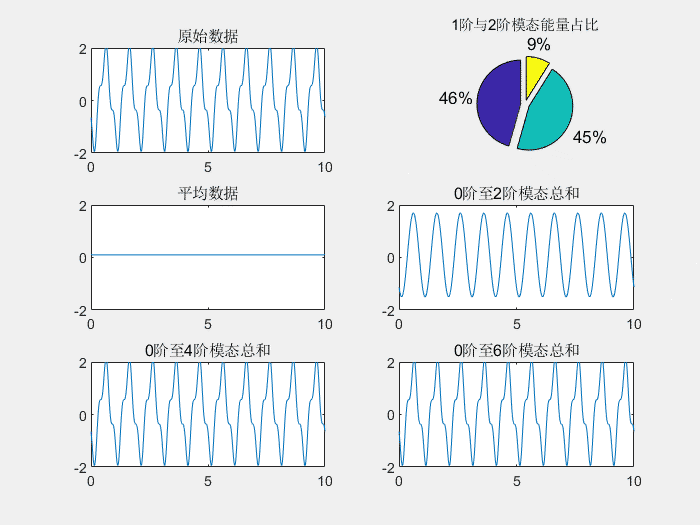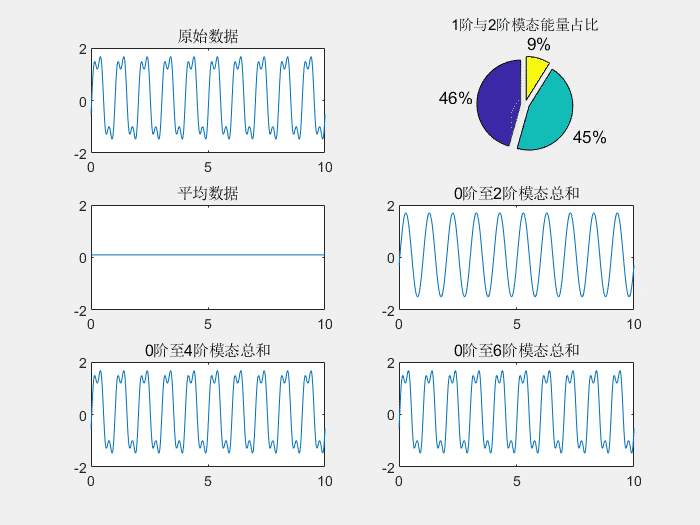
谐波分类
谐波频率是基波频率的整倍数，法国数学家傅立叶证明，任何重复的波形都可以分解为含有基波频率和一系列为基波倍数的谐波的正弦波分量。
谐波含量及波形
波形及谐波含量
根据谐波频率的不同，可以分为：
1、偶次谐波
额定频率为基波频率偶数倍的谐波，被称为“偶次谐波”，如2、4、6、8次谐波。
2、奇次谐波
额定频率为基波频率奇数倍的谐波，被称为“奇次谐波”，如3、5、7次谐波
一般地讲，奇次谐波引起的危害比偶次谐波更多更大。
在平衡的三相系统中，由于对称关系，偶次谐波已经被消除了，奇次谐波占主导地位。对于三相整流负载，出现的谐波电流是6n±1次谐波，例如5、7、11、13、17、19等。六脉整流的三相变频器主要产生5、7次谐波。
3、分数次谐波
当正弦波分量的频率是原交流信号的频率的非整数倍时，称为分数次谐波，当分数大于1时称为间谐波，当分数小于1时，也称次谐波。严格讲，基于傅里叶变换的谐波分析方法中，不存在分数次谐波。