Apollo_ADS_路径规划1_道路中心线表示& 平滑_Reference Line Smoother_路径规划里面的平方积分

参考何为二次规划：

https://wenku.baidu.com/view/41788a34f61fb7360a4c6584.html

---

Must know：

我们有n 个点 （x,y）， 在笛卡尔坐标系下 , 可以拟合一条曲线。Y关于X

同样的，如果在frenet frame 坐标下，ego的坐标（0,0），传感器 拍摄到 n 个车道中心线（曲线）的 坐标，一段一段， 采样时间也是固定的。 --不变道，这条参考线保持不变，在此基础上做后面的S-T , S-L 规划。

对于中心线， 先得到笛卡尔坐标下表示， x 关于 时间t, y 关于时间t, 2个多项式方程

以 车道线中心为参考坐标系。得到 frenet下 ego的坐标（station,lateral）s--arc 沿曲线走过的累计长度，l--横向的offset

随着时间的增加， ego 走过n个点，（s,l） 拟合成一条曲线（N次多项式-可以配置）， L 关于S的方程. 这个就是ego 的行驶轨迹。--站点信息。（实际上就是X,Y的关系）

同样的 S-T frame 下得到， arc length (纵向位置）关于时间的函数，求微分就可以得到速度，加速，jerk  -->得到不同时刻加速还是减速的信息。---完成速度profile 的定义

---

Reference Line Smoother---优化目标是曲线的Jerk

https://github.com/ApolloAuto/apollo/blob/master/docs/specs/reference_line_smoother.md

Quadratic programming（二次规划）） + Spline（样条曲线） interpolation

1. Objective function

1.1 Segment routing path 建立数学模型

Segment routing path into n segments. each segment trajectory is defined by two polynomials（多项式）:

关于时间的多项式函数，x--纵向位置，y--横向位置 ， t=0 ,得到初始点坐标，t=1,1s后的坐标，t=3,3s后的坐标 ...

v恒定时，t可以换成 v*t=arc length

求一次导数得到速度，二阶-加速度，三阶-jerk ...

 

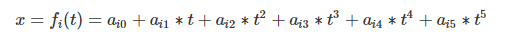
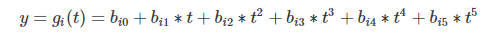
1.2 Define objective function of optimization for each segment  定义目标函数

为什么定义这个形式？三阶导数 ，然后平方，得到的函数再求积分

只是cost 函数的定义方法，同数学里面的方差定义，平方以后可以让误差放大，更容易比较，（去除了符号的影响）， jerk 平方后求累积值（积分）

 

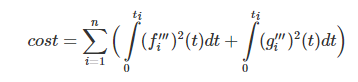
1.3 Convert the cost function to QP formulation 

转换成二次规划的形式--规划问题，核心不是计算，而是如何建模。

QP formulation:

2 Constraints

2.1 Joint smoothness constraints 连接处的平顺性

This constraint smoothes the spline joint. Let's assume two segments, and 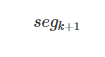, are connected and the accumulated s of segment is  Calculate the constraint equation as:

第一段的从时间t :0---t , arc length 变换 s0-sk  （假设速度恒定，匀速圆周运动， t= s）

第二段一样，时间从0-t+1, arc length 变化：s0-sk+1

连接处2段曲线方程相交，对应的加速度，jerk etc.

 

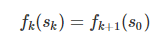
时间都是从s0~sk, 坐标是k段的结束，右边是k+1段的开始。当然连接啦！

Similarly the formula works for the equality constraints, such as:

2.2 Sampled points for boundary constraint

采样点边界约束--路径肯定不可能横向无限宽，纵向无限长。

Evenly sample m points along the path and check the predefined boundaries at those points.