【数据结构】查找（顺序查找、二分查找、索引顺序查找、二叉排序树、平衡排序树、B树、B+树、哈希表）

数据结构——查找

何为查找

1. 查找表

1. 查找表由同一类型的数据元素(或记录)构成的集合

2. 查找表的操作包括：

1. 查询某个特定的数据元素是否在查找表中；
2. 检索某个特定的数据元素的各种属性；
3. 在查找表中插入一个数据元素；
4. 从查找表中删去某个数据元素。

3. 查找表的分类：

1. 静态查找表:只允许做查询和检索操作的查找表。
2. 动态查找表:除查询和检索操作外，还允许进行插入和删除操作的查找表。

2. 关键字

关键字：是**数据元素（或记录）**中某个数据项的值，用以标识（识别）一个数据元素（或记录）

若此关键字可以识别唯一的一个记录，则称之谓**“主关键字”**
若此关键字能识别若干记录，则称之谓**“次关键字”**
查找表的查询和检索通常是根据关键字进行的

根据给定的值，在查找表中确定一个其关键字等于给定值的数据元素或记录

1. 若查找表中存在这样一个记录（数据元素），则称查找成功。查找结果给出整个记录（数据元素）的信息，或指示该记录（数据元素）在查找表中的位置；
2. 否则称此查找不成功。查找结果给出“空记录 ”或“空指针”

3. 查找方法效果评价指标——平均查找长度ASL(Average Search Length)

查找速度：平均查找长度ASL(Average Search Length)-为确定记录在表中的位置，需要与给定值进行比较的次数的期望值叫查找算法的平均查找长度

静态查找表–顺序查找性能分析:
查找成功的平均查找长度（查找成功的情况下，平均找一个数据元素需要的比较次数称为查找成功的平均查找（检索）长度）：
$$ASL=(1+2+\dots +n)/n=(n+1)/2$$
说明：假设每个数据元素查找的概率相同

查找一次的平均检索长度（成功，失败）(*)
$$ASL=(n+1)/2+(1+2+\dots +n)/(2\ast n)=3(n+1)/4$$
说明：假设每个数据元素查找的概率相同，并且查找一次成功和失败的概率也相同

静态查找表

1.顺序查找

查找方法：从表的一端顺序找到表的另一端 (以线性表表示静态查找表)

1. 存储结构无特殊要求(数组或链表都可以的)
2. 元素顺序无要求(有序、无序都可以的 )

//顺序表定义
#define max 100
typedef struct{
	KeyType key; ;//说明：KeyType代表关键字的类型
	//……;
}ElemType 

typedef struct{ 
	ElemType elem[max]; 
	int length;
}SqList;
SqList L;

1
2
3
4
5
6
7
8
9
10
11
12
13

顺序查找：

int search(SqList L, KeyTypex){ 
	//KeyType代表关键字的类型
	for(int i=0;i<L.length;i++)
		if(L.elem[i].key==x) 
			return i+1;//找到数据的位置  +1为了方便表示第几个数据
	return 0;
}
//说明:返回0说明没找到；若找到，返回是x线性表的第几个数据元素
1
2
3
4
5
6
7
8

为提高查找速度，设置哨兵项；查找表组织成线性表，线性表的数据元素从下标为1的数组元素开始存放；下标为0的数组元素作为哨兵项(说明：哨兵可设在低端，也可以设在高端)
查找x，首先将x放在下标为0的数组元素（哨兵），从表尾开始比较。若在哨兵
处相等，说明没找到，否则找到

int srearch(SqList L,KeyTypex)//KeyType代表关键字的类型
{ 
	int k=L.length;
	L.elem[0].key=x;
	while(x!=L.elem[k].key)
		k--;
	return k;
}

//L.elem[0]哨兵项
//说明:返回0说明没找到；若找到，返回是x线性表的第几个数据元素
//说明2：哨兵也可以设在线性表的表尾

1
2
3
4
5
6
7
8
9
10
11
12
13

静态查找表–顺序查找性能分析:
查找成功的平均查找长度（查找成功的情况下，平均找一个数据元素需要的比较次数称为查找成功的平均查找（检索）长度）：
$$ASL=(1+2+\dots +n)/n=(n+1)/2$$
说明：假设每个数据元素查找的概率相同

查找一次的平均检索长度（成功，失败）(*)
$$ASL=(n+1)/2+(1+2+\dots +n)/(2\ast n)=3(n+1)/4$$
说明：假设每个数据元素查找的概率相同，并且查找一次成功和失败的概率也相同

2.二分查找

采用二分查找的要求：查找表组织成有序线性表（递增或递减），且采用顺序存储结构
特点：通过一次比较，将查找范围缩小一半

二分查找通用模板：

// 在单调递增序列a中查找>=x的数中最小的一个（即x或x的后继）
while (low < high)
{
    int mid = (low + high) / 2;
    if (a[mid] >= x)
        high = mid;

    else
        low = mid + 1;
}

// 在单调递增序列a中查找<=x的数中最大的一个（即x或x的前驱）
while (low < high)
{
    int mid = (low + high + 1) / 2;

    if (a[mid] <= x)
        low = mid;

    else
        high = mid - 1;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

二分查找算法原理：

//有序（递增或递减），顺序存储结构
int binaryS(SqList L, KeyType x){

	int low=0, high=L.length-1, m;
	
	 while(low<=high){
	 	m=(low+high)/2;//
	 	
	 	if(L.elem[m].key==x) 
	 		return m+1; //若找到，返回是x线性表的第几个数据元素
	 	if(L.elem[m].key>x) 
	 		high=m-1; 
	 	else 
	 		low=m+1;
	} 
	
	return 0;
}
//说明:返回0说明没找到；若找到，返回是x线性表的第几个数据元素

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

■ 二分查找的效率高，但是要将表按关键字排序。而排序本身是一种很费时的运算。既使采用高效率的排序方法也要花费$O(nlogn)$的时间。
■ 二分查找只适用顺序存储结构。为保持表的有序性，在顺序结构里插入和删除都必须移动大量的数据元素。因此，二分查找特别适用于那种一经建立就很少改动、而又经常需要查找的线性表。
■ 对那些查找少而又经常需要改动的线性表，可采用链表作存储结构，进行顺序查找。链表上无法实现二分查找。（*）

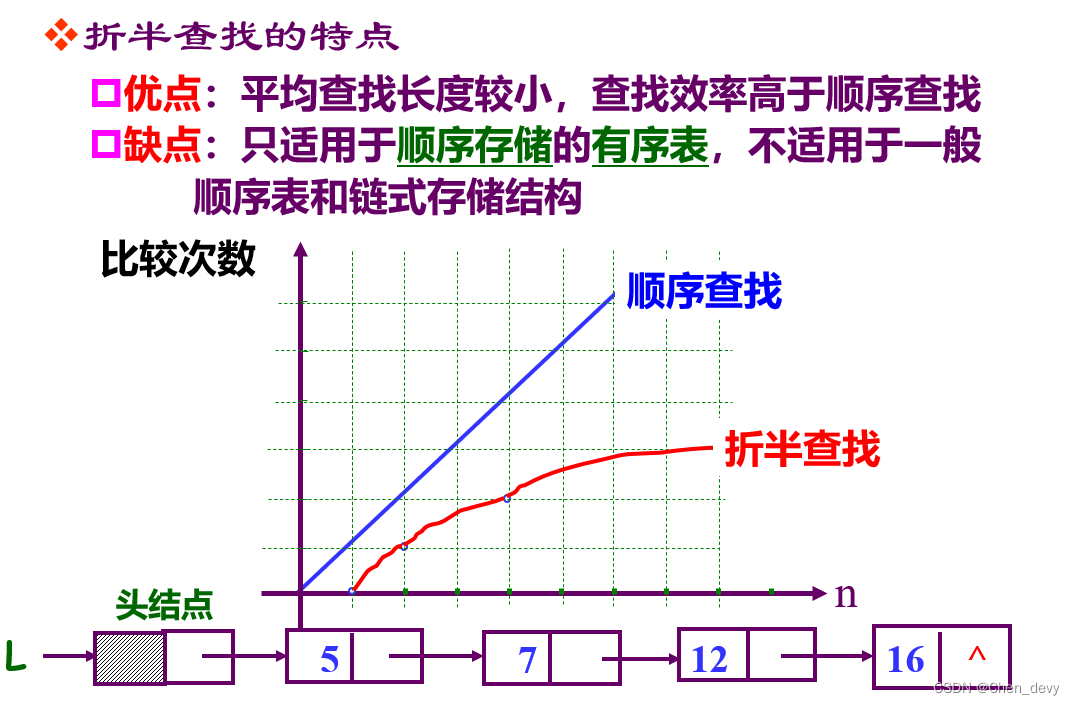
二分查找判定树

3.静态查找表—索引顺序表的查找

线性表分成若干块，每一块中的键值存储顺序是任意的，块与块之间****按键值排序，即后一块中的所有记录的关键字的值均大于前一块中最大键值。

建立一个索引表，该表中的每一项对应于线性表中的一块，每一项由键域（存放相应块的最大键值）和链域（存放指向本块地一个结点的指针）组成。

适用条件：分块有序表

索引顺序表的查找:

■ 首先对索引表采用二分查找或顺序查找方法查找，以确定待查记录所在的块。 ■
在线性表查找k，若其在线性表中存在，且位于第i块，那么一定有：第i-1块的$最大键值<k\le 第i块的最大键值$。 ■
然后在相应的块中进行顺序查找。

数据结构（结构体）：

typedef struct{    
	KeyType key;    //关键字域
    //…… ;                   // 其它域
}ElemType;//数据结构

typedef struct{    
	ElemType *elem;   // 数据元素存储空间基址
    int length;    // 表的长度
}SSTable;//顺序表

typedef struct{  
  	KeyType MaxKey; //本块最大关键字
   	int FirstLink; //本块第一个结点下标
}IndexTable;//索引表的类型

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

索引顺序查找表的算法原理：

int Seach_Index(SSTable ST,IndexTable IT[],int b,int n,KeyType k){  		
	int i=1,j;
	//b 为块儿数  Maxkey为每块儿中的最大值
	//索引表查找
   	while((k>IT[i].MaxKey)&&(i<=b))  
          i++;
          
   	if(i>b){  
   		printf("\nNot found");  
   		return(0); 
   	}
   	
   	j=IT[i].FirstLink;      
   	
   	//块儿内查找
   	while((k!=ST.elem[j].key)&&(ST.elem[j].key<=IT[i].MaxKey)  &&(j<n))
    	j++; 
    
    //输出查找结果	
   if(k!=ST.elem[j].key){
   		j=0; 
   		printf("\nNot found"); 
   	}
   return(j);
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

■ 表长为n的线性表，整个表分为b块，前 b-1块中的记录数为s=⎡n/b⎤，第b块中的记录数小于或等于s。

■ $ASL=(b+1)/2+(s+1)/2$
（*）
■ 当 s = 根号n ，ASL最小 根号n +1

①索引表查找可使用何方法？①顺序、折半查找
②块内查找可使用何方法？ ②只能使用顺序查找
③数据可否用链式存储？ ③可以使用链式存储
对那些查找少而又经常需要改动的线性表，可采用链表作存储结构，进行顺序查找。链表上无法实现二分查找。（*）

动态查找树表

1. 二叉排序树

1. 二叉排序树定义：

二叉排序树或者是一棵空树；或者是具有如下特性的二叉树：

1. 若它的左子树不空，则左子树上所有结点的值均小于根结点的值；
2. 若它的右子树不空，则右子树上所有结点的值均大于根结点的值；
3. 它的左、右子树也都分别是二叉排序树 (递归)

2. 二叉排序树的中序遍历结果递增有序
   判断一棵二叉树是否为二叉排序树：看其中序遍历结果是否递增有序
   因此，一个无序序列，可通过构建一棵二叉排序树而成为有序序列。

3. 二叉排序树的主要作用与操作

■ 二叉排序树主要作用：检索，排序
■二叉排序树主要操作：检索，插入（建立），删除

检索：

■ 在二叉排序树中查找是否存在值为x的结点。
■ 查找过程为：
① 若二叉排序树为空，查找失败。
②否则，将x与二叉排序树的根结点关键字值比较：若相等，查找成功，结束；
否则，
a．若x小于根结点关键字，在左子树上继续进行，转①
b．若x大于根结点关键字，在右子树上继续进行，转①

4. 二叉排序树的存储结构**(二叉链表)**

//二叉链表作为二叉排序树的存储结构
typedef struct NODE{
	int key;//数据元素的关键字
	//… ;//数据元素的其他数据项 
	struct NODE *lc,*rc;
}BiNode,*BiTree;

1
2
3
4
5
6
7
8

2. 二叉树的检索算法

//二叉排序树的检索算法
Bitree Search(BiNode *t, int x){ 
	BiTree p; //
	p=t;
	while(p!=NULL){ //没找到就是返回空指针
		if (x==p->key)  //找到就返回
			return p; 
			
		if (x < p->key) //左右搜索
			p=p->lc;
		else 
			p=p->rc;
}
return p;
}//函数返回查找结果，没找到为空指针！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

3. 二叉排序树的插入算法

向二叉排序树中插入x：
先要在二叉排序树中进行查找，若查找成功， 按二叉排序树定义，待插入数据已存在，不用插入；查找不成功时，则插入之。
新插入结点一定是作为叶子结点添加上去的。(*)

建立一棵二叉排序树则是逐个插入结点的过程。（*）
同一组数据，输入顺序不同，所建二叉排序树不同！

//

int Insert(Bitree &t,int x)//二叉排序树的插入算法
{  
	BiTree q, p, s;
	q=NULL; 
	p=t; ;//p为正在查看的节点，初始从根节点开始；q为p的双亲节点，根节点无双亲节点 			
	while(p!=NULL){ //查找
		if (x==p->key)      
			return 0;//在当前的二叉排序树中找到x，直接返回，不再做插入 
			
		q=p;//记录上一个位置
		
		if (x<p->key) 
			p=p->lc; 
		else 
			p=p->rc;
	}
	//最后没找到的话 就是插入到 q的左孩子或右孩子处
	
	s=(BiTree)malloc(sizeof(Binode)) ;//没找到x，做插入：先申请节点空间 
	s->key=x; //初始化
	s->lc=NULL; 
	s->rc=NULL ;//存放x，设为叶节点
	
	if(q==NULL)t=s;//若原先的二叉树是一棵空树，新插入的x对应的节点s为插入后二叉树的根节点
	//这个很重要 要不然空树 后面插入 就报错了。。。 
	else if(x<q->key) 
		q->lc=s; ;//插入s为q的孩子
	else 
		q->rc=s; 
		
	return 1;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

4. 二叉排序树的删除算法

从二叉排序树中删除一个结点之后，使其仍能保持二叉排序树的特性。

1. 被删结点为叶结点，由于删去叶结点后不影响整棵树的特性，所以只需将被删结点的双亲结点相应指针域改为空指针。
2. 若被删结点只有右子树 pr或只有左子树 pl，此时，只需将pr或pl替换被删结点即可。
3. 若被删结点既有左子树 pl 又有右子树pr ，可按中序遍历保持有序进行调整。

左右孩子均存在
用左子树中最大的结点q的值替换被删结点，再删"q" 或 用右子树中最小的结点w的值替换被删结点，再删"w"
结点q (和w)的特点是最多只有一个孩子

左子树中最大结点的特点是 左子树的根节点一直向右下 直到p->rchild==NULL为真,此时p就是那个左子树中的最大结点。
右子树中最小结点的特点是右子树的根节点一直向左下，直到p->lchild==NULL为真,此时p就是那个右子树中的最小结点。

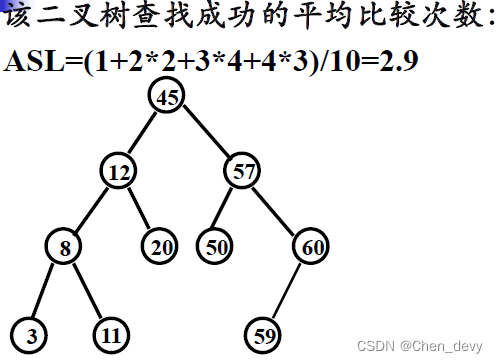
5. 最佳二叉排序树

二叉排序树查找过程与二分查找判定树相似

1. n个数据元素按照不同的输入顺序构造的二叉排序树不同，其中平均查找性能最高的为最佳二叉排序树.

2. 按照二分查找判定树的建立过程建立的二叉排序树为最佳二叉排序树。

3. 二叉排序树的查找速度一般比顺序查找快，但如果是单枝树则一样快。
   注意单枝树的情况

2.平衡二叉树

平衡二叉树(AVL树)（平衡二叉排序树）

希望所建的二叉排序树均为平衡二叉树 (AVL树)
注意需要时刻考虑到 空树 以及 单枝树 的情况

平衡二叉树:空树，或者是具有下列性质的二叉树：

1. 左、右子树都是平衡二叉树 (递归)
2. 左、右子树高度之差的绝对值不超过1
3. 树中每个结点的左、右子树高度之差的绝对值不大于1。

$$结点的平衡因子BF=结点的左子树深度-右子树深度$$
平衡二叉树每个结点的平衡因子的绝对值不超过1

平衡旋转技术

如果在一棵AVL树中插入一个新结点，就有可能造成失衡，此时必须重新调整树的结构，使之恢复平衡。我们称调整平衡过程为平衡旋转。

平衡旋转可以归纳为四类：

1. LL平衡旋转–单向右旋
2. RR平衡旋转–单向左旋
3. LR平衡旋转–先左旋后右旋
4. RL平衡旋转–先右旋后左旋

旋转操作特点

1. 对不平衡的最小子树操作
2. 旋转后子树根节点平衡因子为0
3. 旋转后子树深度不变故不影响全树，也不影响插入路径上所有祖先结点的平衡度

平衡树查找的时间复杂度为O(logn)

LL型—单向右旋

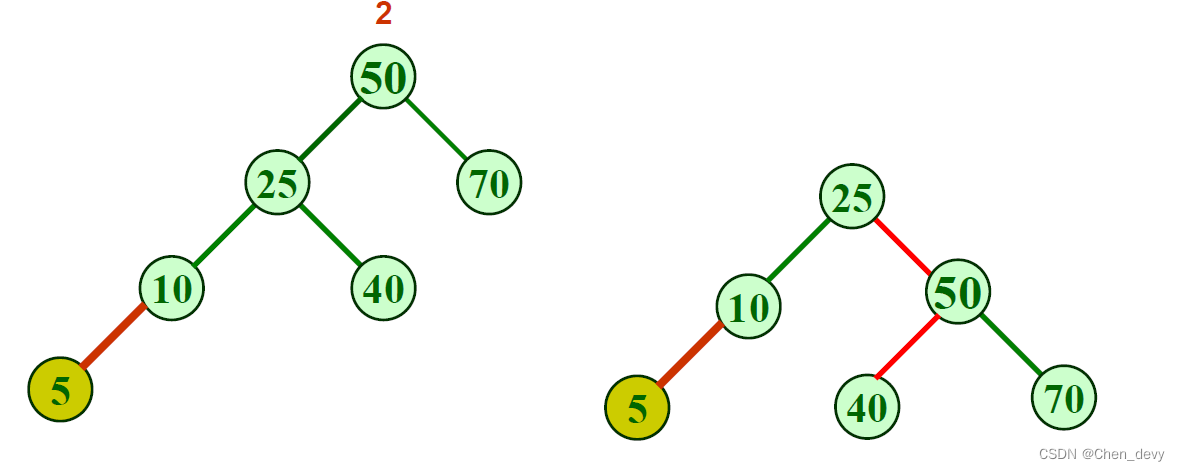
RR型—单向左旋

LR型—先左旋后右旋:
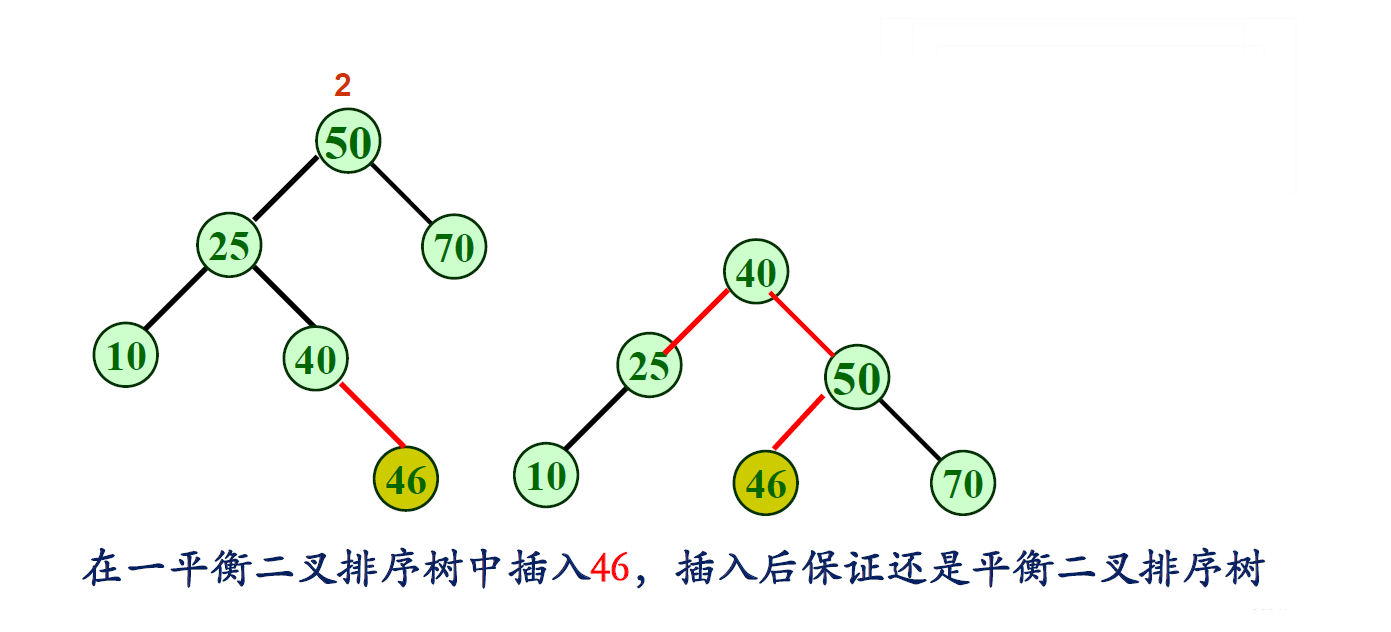RL型—先右旋后左旋

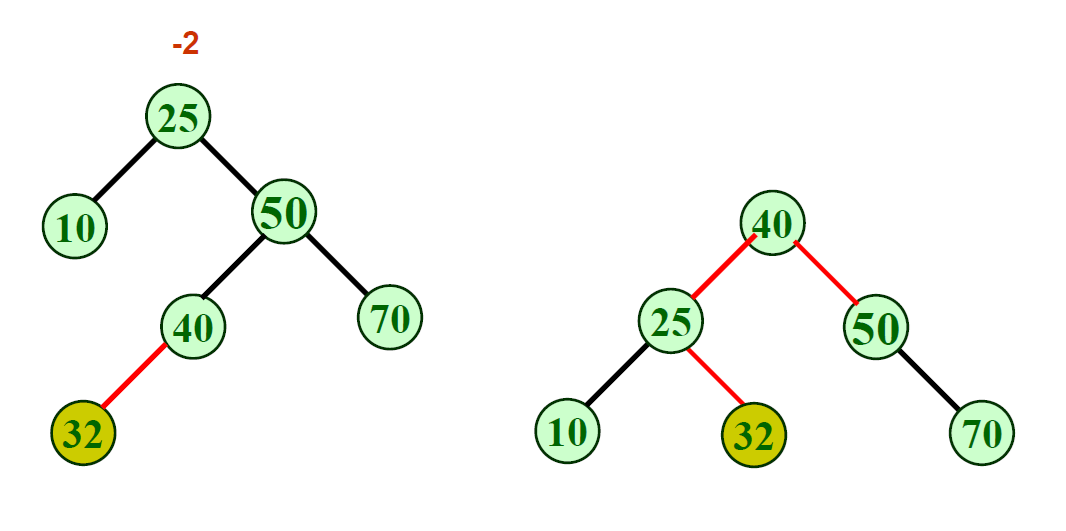
在平衡树上进行查找的过程和二叉排序树相同，因此，查找过程中和给定值进行比较的关键字的个数不超过平衡二叉树的深度。
(*)

B-树 和B+树

动态查找表，允许：查找，插入和删除操作

B-树是一种平衡的多路查找树。

哈希表查找

不同的表示方法，其差别仅在于：关键字和给定值进行比较的顺序不同

哈希函数是一个映象，即：将关键字的集合映射到某个地址集合上，它的设置很灵活，只要这个地址集合的大小不超出允许范围即可

哈希表构造方法：

哈希表"冲突"现象——冲突处理

实际应用中不保证总能找到一个不产生冲突的哈希函数。一般情况下，只能选择恰当的哈希函数，使冲突尽可能少地产生。

冲突处理方法：

1. 开放定址法
2. 再哈希表法
3. 链地址法
4. 建立一个公共溢出区

1. 开放定址法

$d_i$称为增量，有三种取法：

1. 线性探测再散列: $d_i=i$
2. 平方(二次)探测再散列: $d_i=1^2,-1^2,2^2,-2^2,3^2,-3^2,\dots$
3. 随机探测再散列: $d_i$ 是一组伪随机数列

增量$d_i$ 应具有“完备性”(*)

2. 再哈希表法

3. 链地址法

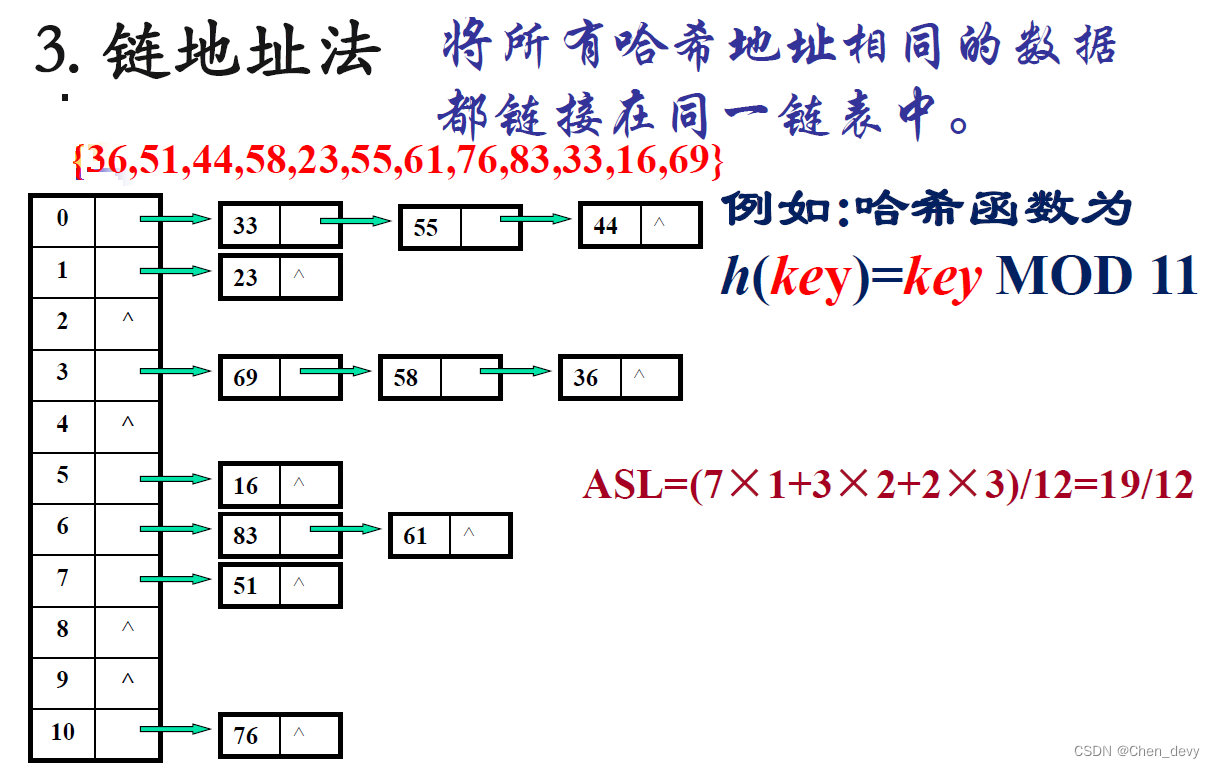
4. 建立一个公共溢出区

将发生冲突的数据元素顺序存放于一个公共的溢出区

哈希表的查找

查找过程和造表过程一致
哈希表饱和的程度，装载因子 $\alpha =n/m$ 值的大小（n—数据数，m—表的长度）

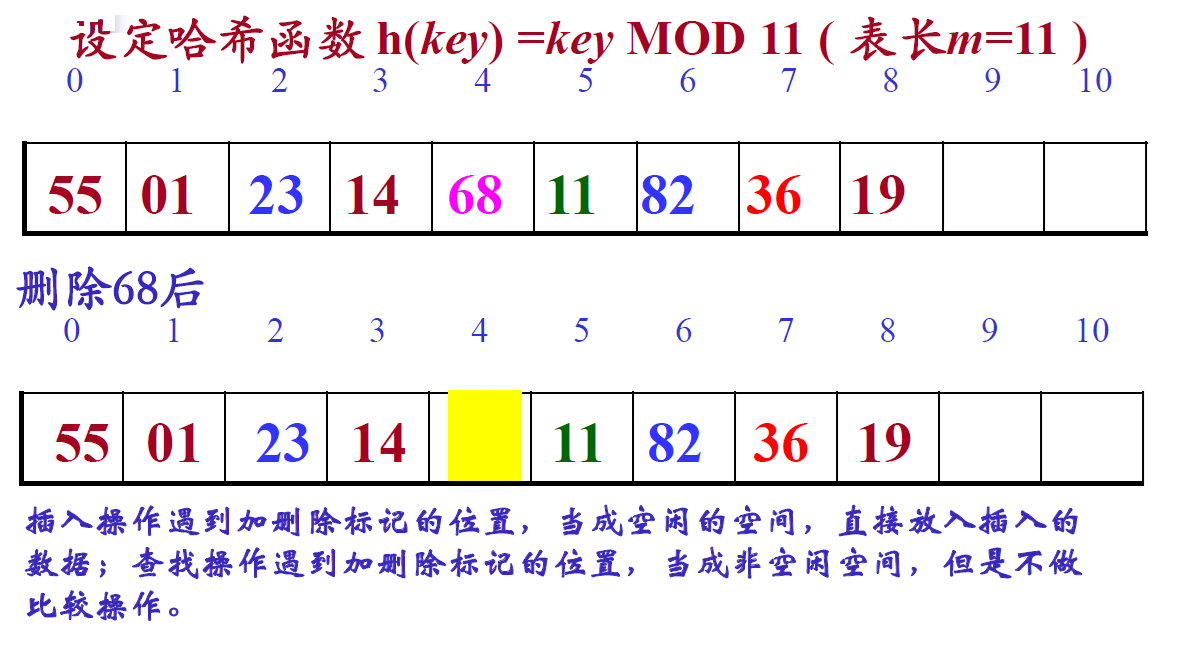
哈希表的删除操作

开放定址法：删除一个数据，为保证查找工作的正常进行不能真删----加删除标志