数据正态分布化 + 基于回归算法的房价预测（含python代码）_xgb回归

本文用到的美国房屋数据，数据介绍详见我的上一篇文章：

链接：https://pan.baidu.com/s/1wrkzFF87A_Emgid_s7K3aA
提取码：2j77 

内含两个文件：

data_train.csv：训练集数据，包含房价等81个指标；

data_test.csv：测试集数据，不包含房价；

文章目录

前言

一、数据预处理

1. 删除异常值

2. 填补缺失值

3. 转换数据类型

4. 建立值与类别的映射 

二、对房价进行正态分布化处理：

         第一步：在原数据的柱状图上添加正态分布概率密度曲线和核密度估计曲线；

         第二步：对房价进行正态分布化处理；

         第三步：添加一列总面积并计算偏度；

         第四步：随后对偏度大的列数据进行BOX-COX转换，改善数据的正态性和对称性；

         第五步：对数据进行独热编码；

三、使用多个回归预测算法进行房价预测

1. 导入包和数据

2. 定义模型

3. 定义训练数据和计算模型均方根误差的方法

4. 通过均方误差评估各模型效果

5. 模型应用（预测）

---

前言

紧接上一篇文章，本文针对数据进行了正态化处理，应用了Lasso、KernelRidge、ElasticNet、GradientBoostingRegressor、XGBRegressor等回归模型进行房价预测。

数据长这样，数据集的具体解释和分析详见我的上一篇文章：

---

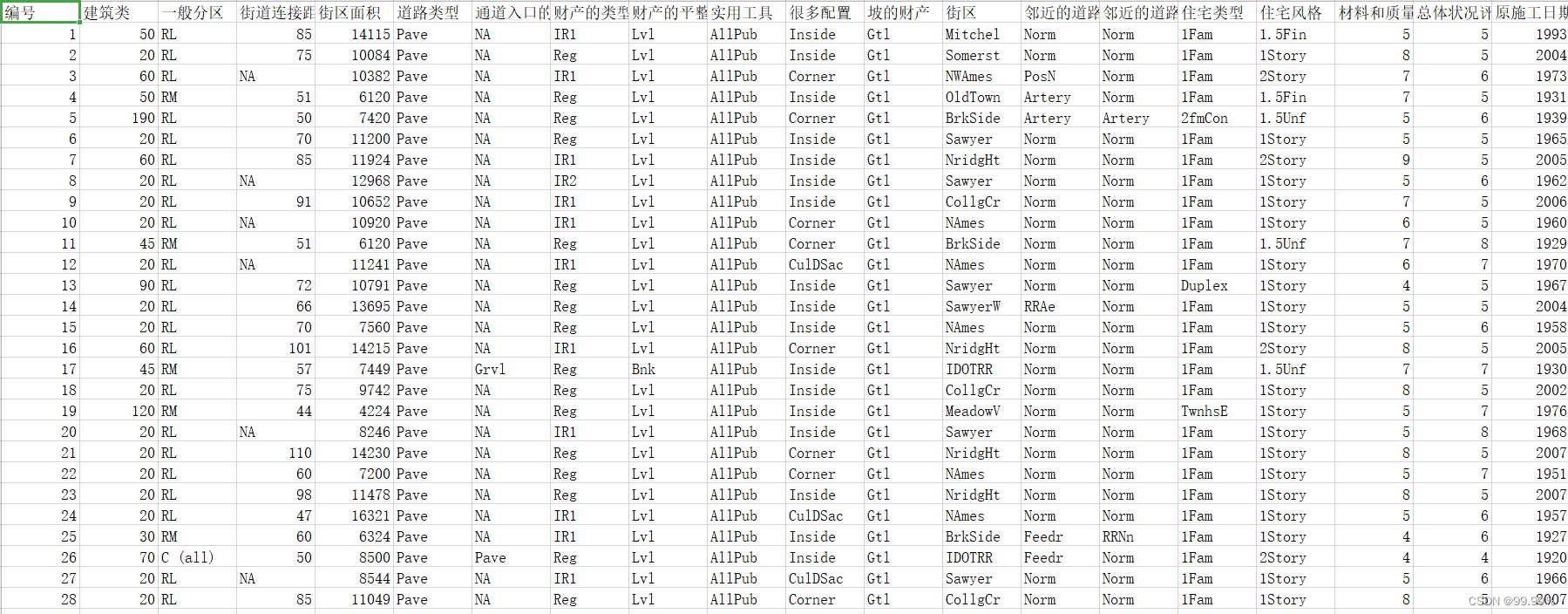
一、数据预处理

导入包：

#不显示警告
import warnings
warnings.filterwarnings('ignore')
 
#数据处理，数据分析
import numpy as np
import pandas as pd
 
#统计计算相关的工具包
import math
from scipy import stats
from scipy.stats import norm
 
#画图相关的工具包
import seaborn
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties
%matplotlib inline

1. 删除异常值

df_train = pd.read_csv('data_train.csv',encoding='gbk')#读入数据文件
# 统计各属性的缺失值个数，并按照降序排序
total_isnull = df_train.isnull().sum().sort_values(ascending=False)
# 统计各行总数
total_number_rows=len(df_train)
# 统计缺失值占比
percent = (total_isnull/total_number_rows)*100
# 拼接两列
missing_data = pd.concat([total_isnull, percent], axis=1, keys=['缺失值数量', '百分比'])
# 查看前20行
missing_data.head(20)

# 读取训练集数据
train = pd.read_csv('data_train.csv',encoding='gbk')
# 读取测试集数据
test = pd.read_csv('data_test.csv',encoding='gbk')
# 查看训练集数据形状
print("The train data size before dropping Id feature is : （%d %d）" %(train.shape[0],test.shape[1]))
# 查看测试集数据形状
print("The test data size before dropping Id feature is : （%d %d）\n" %(test.shape[0],test.shape[1]))
# 删除两个数据集中编号属性列
train.drop("编号", axis = 1, inplace = True)
test.drop("编号", axis = 1, inplace = True)

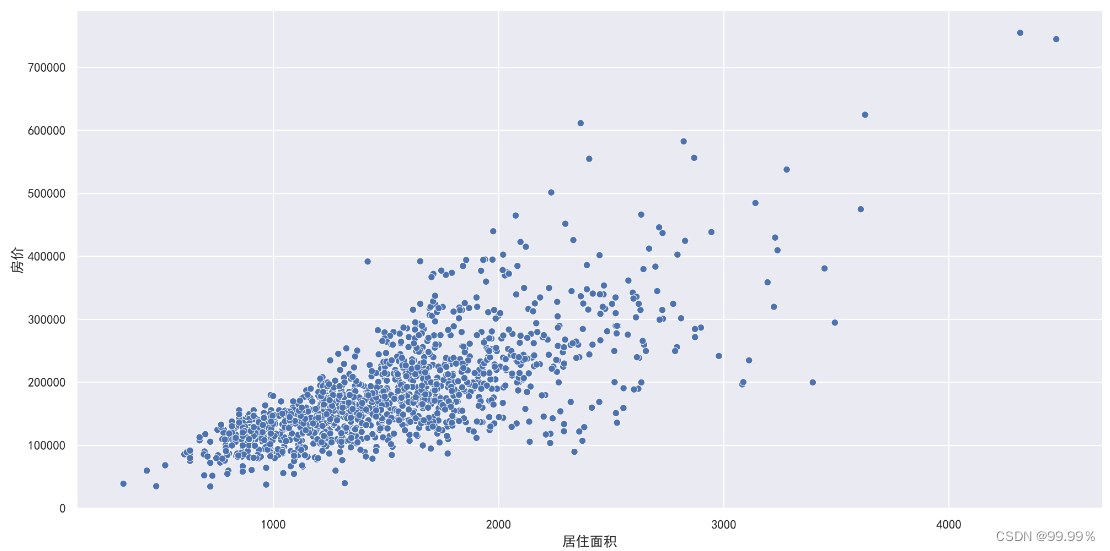
查看离群点，作居住面积与房价的散点图，发现右下角存在离群点。 

# 设置图片样式
plt.figure(figsize=(16, 8),dpi=600)
# 绘制“住房面积” “房价散点图”
fig = seaborn.scatterplot(train['居住面积'],train['房价'])

删除离群点，再次作居住面积与房价的散点图，观察离群点是否已经被删除。 

train = train.drop(train[(train['居住面积']>4000) & (train['房价']<300000)].index)#删除离群点
 
plt.figure(figsize=(16, 8),dpi=600)#设置图片大小
fig = seaborn.scatterplot(train['居住面积'],train['房价'])#作散点图

2. 填补缺失值

#计算所有特征缺失值占比
all_data_na = (all_data.isnull().sum() / len(all_data)) * 100
 
#去掉不包含缺失值的属性，并对剩下的属性按照缺失值比例降序排序，存下排名前10的属性
all_data_na = all_data_na.drop(all_data_na[all_data_na == 0].index).sort_values(ascending=False)[:10]
#转换成DataFrame的格式
missing_data = pd.DataFrame({'缺失值占比' :all_data_na})
#展示
missing_data

填补缺失值。根据特征的现实意义，采用”None“进行填充：

cols = ('泳池质量','车库类型', '车库室内装修', '车库质量', '车库条件','地下室的高度','地下室的条件','花园层地下室墙',
        '地下室基底质量','地下室第二成品区质量','砌体饰面型','砌体饰面型','杂项功能','通道入口的类型',
        '栅栏的质量','壁炉质量','建筑类','实用工具') #将需要转换的列存入元组                     
 
for col in cols:
    all_data[col] = all_data[col].fillna('None')
    
all_data['泳池质量']

#先利用groupby函数将数据按照“街区”进行分组，取出‘街道连接距离’这一列
list(all_data.groupby('街区')['街道连接距离'])[0:3]
 
cols = ('车库修筑年份','车库规模','车库车位数量','地下室基底面积','地下室第二成品区面积',
        '未使用的地下室面积','地下室总面积','地下室全浴室','地下室半浴室','砌体饰面面积','砌体饰面面积') #将需要转换的列存入元组               
for col in cols:
    all_data[col] = all_data[col].fillna(0)
    
cols = ('一般分区','电气系统','厨房的品质','第一外部材料','第二外部材料','家庭功能评级','销售类型')  #将需要转换的列存入元组                
for col in cols:
    all_data[col] = all_data[col].fillna(all_data[col].mode()[0]) 

此时再检查缺失值，发现已经全部填补完全：

all_data_na = (all_data.isnull().sum() / len(all_data)) * 100#计算缺失值比例
all_data_na = all_data_na.drop(all_data_na[all_data_na == 0].index).sort_values(ascending=False)#去掉不包含缺失值的属性并对剩下的属性排序
missing_data = pd.DataFrame({' 缺失值占比' :all_data_na})#转换成数据框格式
missing_data.head()#显示前几行

3. 转换数据类型

转换数据类型，方便后期操作：

all_data['建筑类'] = all_data['建筑类'].apply(str)#将数据转成字符串的形式
all_data['总体状况评价'] = all_data['总体状况评价'].apply(str)
all_data['销售年'] = all_data['销售年'].apply(str)
all_data['销售月'] = all_data['销售月'].apply(str)

4. 建立值与类别的映射 

from sklearn.preprocessing import LabelEncoder
cols = ('壁炉质量', '地下室的高度', '地下室的条件', '车库质量', '车库条件', 
        '外部材料质量', '外部材料条件','加热质量', '泳池质量', '厨房的品质', '地下室基底质量', 
        '地下室第二成品区质量', '家庭功能评级', '栅栏的质量', '花园层地下室墙', '车库室内装修', '坡的财产',
        '财产的类型', '车道', '道路类型', '通道入口的类型', '中央空调', '建筑类', '总体状况评价', 
        '销售年', '销售月')#将需要转换的列存入元组                      
 
for c in cols:
    myLabel = LabelEncoder()#创建labelEncode对象
    myLabel.fit(list(all_data[c].values))#建立值与类别的映射关系
    all_data[c] = myLabel.transform(list(all_data[c].values))#将每一个值按照映射关系进行转换
        
print('Shape all_data: (%d,%d)'%(all_data.shape[0],all_data.shape[1]))    

二、对房价进行正态分布化处理：

第一步：在原数据的柱状图上添加正态分布概率密度曲线和核密度估计曲线；

(mu, sigma) = norm.fit(train['房价'])#计算变换前的均值和方差
print("\n mu = %.2f and sigma = %.2f\n" %(mu,sigma))#打印均值和方差
 
#画出变换前房价的核密度估计曲线，拟合出的生态分布密度概率曲线
plt.figure(figsize=(16, 8),dpi=600)#设置图片大小，分辨率
plt.ylabel('概率密度')#设置纵轴标签
plt.title('房价分布')#设置图片标题
#第一个参数为房价数据，fit=norm代表绘制生态分布密度概率曲线（黑色曲线），kde=True代表绘制核密度估计曲线（蓝色曲线）
#fit_kws，kde_kws，hist_kws分别可以设置黑色曲线，蓝色曲线和直方图的图例标签。
seaborn.distplot(train['房价'] ,fit=norm,kde=True,fit_kws={"label":"正态分布概率密度曲线"},
                 kde_kws={"label":"核密度估计曲线"},hist_kws={"label":"房价频数"})#绘图
plt.legend()#设置图例
 
plt.figure(figsize=(16, 8),dpi=600)#设置图片大小
res = stats.probplot(train['房价'], plot=plt)#计算概率图的分位数，plt是绘图对象，plot=plt显示该图

 

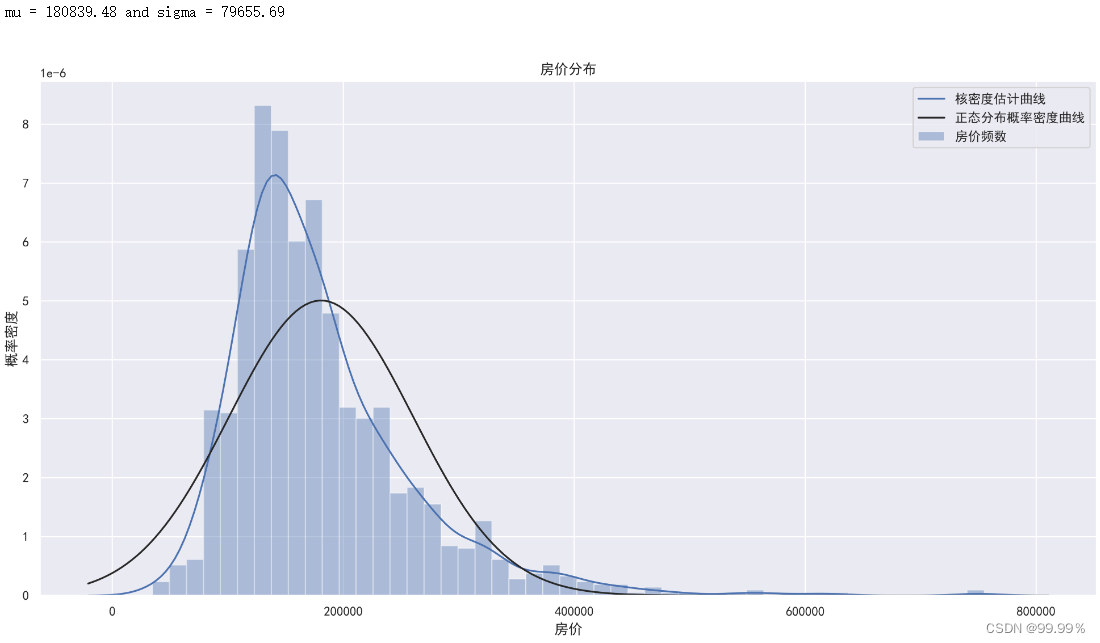
上述结果解释： 第一张图中的蓝色直方图代表对应区间房价的频数，蓝色曲线为和核密度估计曲线，黑色的曲线代表以房价的均值和方差拟合出的正态分布概率密度曲线。可以看出，观测数据的分布与正态分布有一定差距，故应对观测数据进行正态分布化处理。

第二张图为Q—Q图。

蓝色的作图方法：1、找出标准正态分布的所有分位点作为X轴刻度值；2、找出与X轴上所有分位点对应的样本分位点，以标准正态分布分位点为横坐标，样本分位点为纵坐标，可以做出Q-Q图中蓝色的点；

红色线的作图方法：1、以样本的均值和方差生成一组正态分布样本（对应第一张图中黑色曲线）；2、找出与X轴上所有分位点对应的正态分布样本的分位点，以标准正态分布分位点为横坐标，正态分布分位点为纵坐标，可以做出Q-Q图红色直线。

结论：蓝色的点越贴近直线，越说明观测数据的分布贴近正态分布

对房价进行正态分布化处理，计算变换后的均值和方差，作频数直方图、拟合后的正态分布概率密度曲线、Q-Q图。

第二步：对房价进行正态分布化处理；

train["房价"] = np.log1p(train["房价"])#对数变换ln(1+x)
 
(mu, sigma) = norm.fit(train['房价'])#计算新的均值和方差
print("\n mu = %.2f and sigma = %.2f\n" %(mu,sigma))#打印均值和方差
 
plt.figure(figsize=(16, 8),dpi=600)#设置图片大小
plt.ylabel('概率密度')#设置纵轴标签
plt.title('房价分布')#设置图片标题
#第一个参数为房价数据，fit=norm代表绘制生态分布密度概率曲线（黑色曲线），kde=True代表绘制核密度估计曲线（蓝色曲线）
#fit_kws，kde_kws，hist_kws分别可以设置黑色曲线，蓝色曲线和直方图的图例标签。
seaborn.distplot(train['房价'] ,fit=norm,kde=True,fit_kws={"label":"正态分布概率密度曲线"},
                 kde_kws={"label":"核密度估计曲线"},hist_kws={"label":"房价频数"})#绘图
plt.legend()#设置图例
 
 
plt.figure(figsize=(16, 8),dpi=600)#设置图片大小
res = stats.probplot(train['房价'], plot=plt)#画出Q-Q图

 

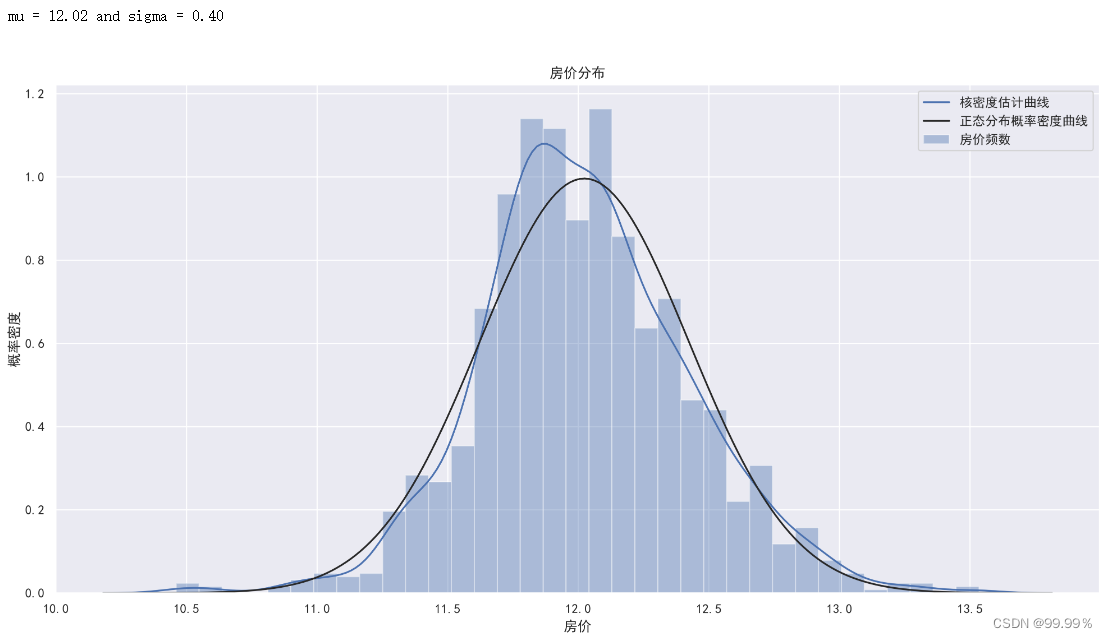
上述结果解释：正态分布化处理后，核密度估计曲线与拟合出的正态分布概率密度曲线更加贴近，Q-Q图中蓝色的点相比处理前更加贴近直线。因此可以认为经过对数变换后的房价数据近似服从正态分布，可以用于接下来的回归任务。

第三步：添加一列总面积并计算偏度；

#增加一个新特征总面积
all_data['总面积'] = all_data['地下室总面积'] + all_data['一楼面积'] + all_data['二楼面积']
 
from scipy.stats import norm, skew
numeric_feats = all_data.dtypes[all_data.dtypes != "object"].index#找出所有数值型属性的索引值
skewed_feats = all_data[numeric_feats].apply(lambda x: skew(x)).sort_values(ascending=False)#计算所有数值型属性的偏度值
print("\n所有数值型特征的偏度为: \n")#打印
skewness = pd.DataFrame({'偏度值' :skewed_feats})#转换成数据框
skewness.head(10)#查看前十行

第四步：随后对偏度大的列数据进行BOX-COX转换，改善数据的正态性和对称性；

skewness = skewness[abs(skewness) > 0.75]#保留偏度的绝对值大于0.75的特征
print("总共有 %d 个特征需要进行BOX-COX变换" %skewness.shape[0])#打印有多少个特征需要进行变换
from scipy.special import boxcox1p
skewed_features = skewness.index#将特征名称保存在skewed_features中
lam = 0.15#一般情况下0.15为经验值。
for feat in skewed_features:
    all_data[feat] = boxcox1p(all_data[feat], lam)#进行BOX-COX转换

第五步：对数据进行独热编码；

使用独热编码来解决类别型数据的离散值问题，方便分析和预测，独热编码的具体原理在此不做详细介绍（就是使用0和1标记数据类别）；

all_data = pd.get_dummies(all_data)#热编码
print(all_data.shape)#打印数据形状。

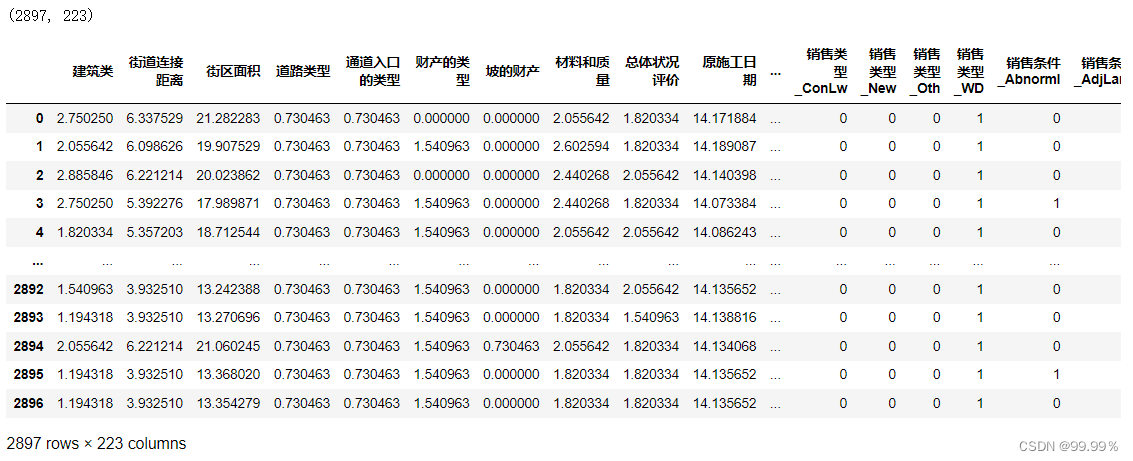
三、使用多个回归预测算法进行房价预测

1. 导入包和数据

from sklearn.pipeline import make_pipeline#级联其他的函数工具
from sklearn.preprocessing import RobustScaler#自动处理离群点的函数
from sklearn.linear_model import ElasticNet, Lasso#弹性回归，套索回归。
from sklearn.kernel_ridge import KernelRidge#核岭回归
from sklearn.ensemble import GradientBoostingRegressor#梯度提升回归
import xgboost as xgb#xgb包中包括极端梯度提升回归模型：XGBRRegressor
#自定义的集成模型类需要寄存sklearn中的三个类：估计器的基类，转换器的混合类，回归估计器的混合类，clone是产生克隆估计器的函数
from sklearn.base import BaseEstimator, TransformerMixin, RegressorMixin, clone
#用于划分数据集，计算模型得分的函数
from sklearn.model_selection import KFold, cross_val_score,train_test_split
 
train = all_data[:ntrain]#定义训练集
test = all_data[ntrain:]#定义测试集

2. 定义模型

共使用5种回归模型，分别为Lasso、KernelRidge、ElasticNet、GradientBoostingRegressor、XGBRegressor模型。

Lasso模型是在线性回归模型的基础上加入了L1正则化的回归方法；

KernelRidge 带有核函数的岭回归模型，岭回归也是在线性回归模型的基础上加入了12正则化的回归方法；

ElasticNet 是套索回归和岭回归的混合模型，同时引入了L1和L2正则化项；

GradientBoostingRegressor 梯度提升回归模型，是一种袋成回归算法；

XGBRegressor 极端梯度提升回归模型，是在梯度提升回归慕础上经过优化的集成回归算法；

#alpha代表正则化惩罚力度，random_state指随机种子
#正则化项为alpha*//w//_l
Lasso = Lasso(alpha =0.0005, random_state=0)
 
 
#alpha代表正则化器罚力度
#正则化项为0.5xalphax//w// 2 2
#kernel=polynomial”指核函数的类型为多项式核函数，K(xxi)=“x*xi)+r)的d次方，degree指poly核中参数d 
KRR = KernelRidge(alpha=0.6, kernel='polynomial', degree=2)
 
 
#alpha代表正则化惩罚力度,randomstate指随战种子
#正则化项为alpha xll ratio & //w// 1 +05 xalpha a (l -ll ratio) a //w// 2 2
ENet = ElasticNet(alpha=0.0005, l1_ratio=.9, random_state=0)
 
 
#nestimators值弱学习器的数目，learningrate值学习率，maxdep场指每个学习器的最大深度:
#max features特征子集中的特征个数，maxfeatures=“sart’代表取特征总数的开方:randomstate指随机种子
GBR = GradientBoostingRegressor(n_estimators=3000, learning_rate=0.05,
                                   max_depth=4, max_features='sqrt', random_state =0)
 
 
#nestimators代表指弱学习器的数目:learningrate指学习率:maxdept指树的最大深度
#regalpha指权重的LI正则化项:reglambda指权重12正则化项:
XGBR = xgb.XGBRegressor(n_estimators=2200,learning_rate=0.05, max_depth=3, 
                        reg_alpha=0.4640, reg_lambda=0.8571)

3. 定义训练数据和计算模型均方根误差的方法

class AveragingModels(BaseEstimator, RegressorMixin, TransformerMixin):
    def __init__(self, models):
        self.models = models
    #定义原始模型的克隆来训练数据。    
    def fit(self, X, y):
        self.models_ = [clone(x) for x in self.models]
        #训练克隆模型
        for model in self.models_:
            model.fit(X, y)
        return self
    #对克隆模型进行预测并求平均
    def predict(self, X):
        #column_stack将3个n*1的矩阵拼接成n*3的矩阵
        predictions = np.column_stack([
            model.predict(X) for model in self.models_
        ])
        return np.mean(predictions, axis=1)#axis=1:压缩列，对各行求均值，返回n*1矩阵。  
 
class StackingAveragedModels(BaseEstimator, RegressorMixin, TransformerMixin):
    def __init__(self, base_models, meta_model, n_folds=5):
        self.base_models = base_models
        self.meta_model = meta_model
        self.n_folds = n_folds
        #定义原始模型的克隆来训练数据
    def fit(self, X, y):
        self.base_models_ = [list() for x in self.base_models]
        self.meta_model_ = clone(self.meta_model)
        
        kfold = KFold(n_splits=self.n_folds, shuffle=True, random_state=0)
        #训练克隆的基础模型（第一阶段的模型），将产生的预测结果存入out_of_fold中，利用out_of_fold中的数据训练元模型（第二阶段的模型）
        out_of_fold_predictions = np.zeros((X.shape[0], len(self.base_models)))
        for i, model in enumerate(self.base_models):
            for train_index, holdout_index in kfold.split(X, y):
                instance = clone(model)
                self.base_models_[i].append(instance)
                instance.fit(X[train_index], y[train_index])
                y_pred = instance.predict(X[holdout_index])
                out_of_fold_predictions[holdout_index, i] = y_pred  
        #现在将out_of_fold里的数据作为特征，拿到元模型（第二阶段）的模型中进行拟合
        self.meta_model_.fit(out_of_fold_predictions, y)
        return self
    #用所有的基础模型（第一阶段的模型）预测测试集上的数据，将预测结果的平均值拿到元模型中进行最后的预测，返回的是一个n*l的矩阵
    def predict(self, X):
        #base_models是一个3*5的二维列表，如下
        #每一行代表一个基模型5次交叉验证生成的5个模型，一共有三个基模型，所以有三行
        
        #np.column_stack([model.predict(X) for model in base_models]).mean(axis=1)对每一行5个模型的预测结果求均值
        #外层的np.column_stack将三个基模型的预测结果拼接成n*3的矩阵
        #因此，meta_features是一个n*3的矩阵，每一列代表一个基模型5次交叉验证的预测的平均值，共有3个基模型所以有三列
        meta_features = np.column_stack([
            np.column_stack([model.predict(X) for model in base_models]).mean(axis=1)
            for base_models in self.base_models_ ])
        return self.meta_model_.predict(meta_features)
 
n_folds = 5#交叉验证的折数
def rmse_cv(model):#编写函数，计算各个模型的均方根误差
    kf = KFold(n_folds, shuffle=True, random_state=0).get_n_splits(train.values)#划分交叉验证需要用到的数据集
    #scoring="neg_mean_squared_error"是计算均方差回归损失，返回值是负值，故要在函数外添加负号，再开平方，得到均方根误差
    rmse= np.sqrt(-cross_val_score(model, train.values, y_train, scoring="neg_mean_squared_error", cv = kf))#计算均方根误差
    return(rmse)

4. 通过均方误差评估各模型效果

单独评估各回归模型： 

 综合评估模型组合：

5. 模型应用（预测）

 选用均方误差最小的stacked_averaged_models4进行应用，预测测试集的房价数据：

stacked_averaged_models4.fit(np.array(train),y_train)
y_pred=stacked_averaged_models4.predict(test)
 
y_pred_real=[]
for i in range(len(y_pred)):
    y_pred_real_i=pow(math.exp(1),y_pred[i])-1
    y_pred_real.append(y_pred_real_i)
 
plt.figure(figsize=(20,8),dpi=600)
plt.plot(y_pred_real[0:200],'bo')
plt.xlabel('样本编号')#设置横轴标签
plt.ylabel('预测房价')#设置纵轴标签
 
plt.show()