「Atcoder」abc238 题解_and and sumatcoder

A - Exponential or Quadratic Editorial

解题思路

由数学归纳法可以证明当n >= 5时一定有$2^n>n^2$
而n小于5时，只有当n = 3时才有$2^n>n^2$

代码

#include<bits/stdc++.h>
using namespace std;

int main()
{
	int n; cin >> n;
	if(2 <= n && n <= 4) cout << "No" << endl;
	else cout << "Yes" << endl;
}
1
2
3
4
5
6
7
8
9

B - Pizza

题目大意

一个披萨，在上面切上n刀，每切一次将披萨顺时针旋转$A_i$度
切完后找出最大的那块披萨(即圆心角最大)，输出最大的圆心角

解题思路

本题采用逆向思维，题目中是将pizza顺时针旋转，其实就相当于将刀逆时针旋转

对于第1刀,刀沿逆时针旋转过的角度为0，  
对于第2刀，刀沿逆时针旋转过的总角度为a[1];  
对于第3刀，刀沿逆时针旋转过的总角度为(a[1] + a[2]) % 360;  
对于第4刀，刀沿逆时针旋转过的总角度为(a[1] + a[2] + a[3]) % 360;  
1
2
3
4

我们假设第1，2，3刀总角度分别为0，120，180…
则第1个圆心角为120-0=120，第1个圆心角为180-120=60…

TIPS:360在圆中等同于0， 而本题第一刀永远为0，所以对于输入处理后从0开始%360循环找出最大圆心角

代码

#include <bits/stdc++.h>
using namespace std;
const int N = 360;

int n, p, x;
bool st[N];  // 表示此处是否被切过

int main()
{
    cin >> n;

    st[0] = true;  // 第1刀永远为0，标记为切过
    for (int i = 0; i < n; i++)
    {
        cin >> x;
        p += x, p %= 360;  // 在之前的位置x的基础上接着逆时针旋转；
        st[p] = true;
    }
    
    int res = 0, cur = 0;
    for (int i = 0; i <= 360; i++)  // 从0遍历到360即可，因为圆只有360
    {
        if (st[i % 360]) res = max(res, cur), cur = 0;  // 如果找到被切过的位置，比较大小
        cur++;  // 可以理解为每次走过1度
    }

    cout << res << endl;
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

C - digitnum

题目描述

$f(x)$的意思是跟x的位数相同且不大于x的数字个数(不含0)

解题思路

打表发现规律

f(1) = 1, f(2) = 2, f(3) = 3 ······ f(9) = 9,
f(10) = 1, f(11) = 2, f(12) = 3 ······ f(99) = 90,
f(100) = 1, f(101) = 2, f(102) = 3 ······ f(999) = 900,
1
2
3

我们可以发现,位数相同的数是1,2,3···9这样连续的排序下去
于是我们可以对N进行不同位数的分别求和，然后相加
假设N是四位数,x是三位数时,可以直接用900*(900+1)/2求出所有三位数的f(x)值
而当x是四位数时,就得用n-1000+1得出项数,n-1000+1+1得出首末之和

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod = 998244353;

ll n, ans;

int main()
{
    cin >> n;
    ll x = n, t = 0, len = 0;  // t用来表示跟N相同位数的最小数,比如N是2022的话,t就是1000
    while (n) {len++,n /= 10,t = t == 0 ? t = 1 : t *= 10;}  // 求出数字位数

    if (len == 1) 
        for (int i = 1; i <= x; i++)    ans += i;
    else 
    {
        ll num = 9;  // 表示项数
        for (int i = 1; i < len; i++)  // 枚举最后一位之前
        {
            ans = (ans + (num * (num + 1)) / 2 % mod) % mod;  // num + 1是首项+末项
            num = num * 10 % mod;
        }

        // 最后一位需要特殊处理
        num = (x - t + 1) % mod;  // 通过这一步可以得到长度为N.size()时的项数(最后)
        ans = (ans + (num * (num + 1)) / 2 % mod) % mod;
    }
    cout << ans;
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

D - AND and SUM

题目描述

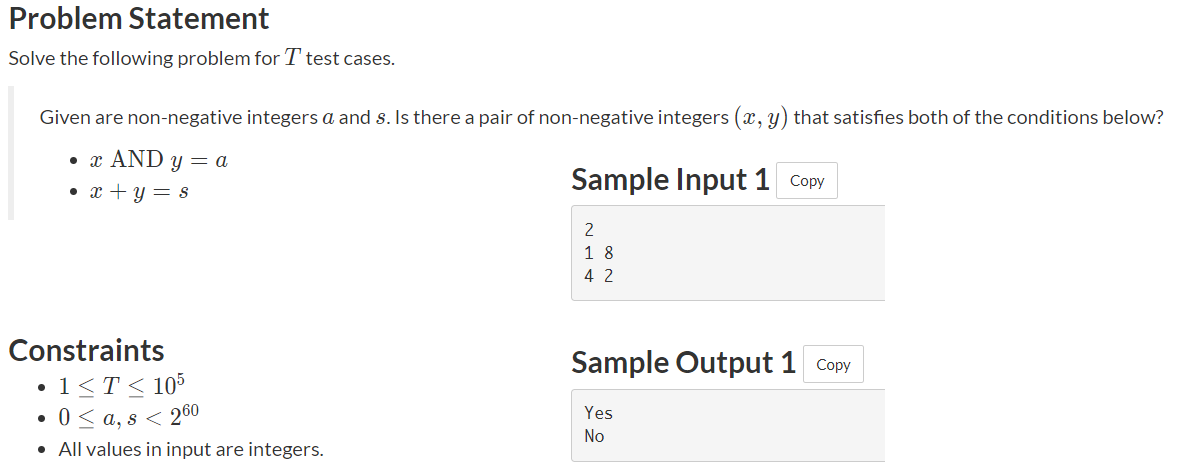
解题思路

$\because x\&y=a$
$\therefore x\ge a且y\ge 等价于x+y\ge 2a$
又$\because x+y=s$
$\therefore 符合条件之一是s\ge 2a$
假设$A$集合中存放$x,y$上都是1的位置，则有$x_a=a$
假设$B$集合中存放$x,y$上其中一个是1的位置(即不全为1),则$B=s-2a$
TIPS:显然$A\cap B=\varnothing$
因此$(s-2a)\&a=0$是符合条件之二

举例证明：
CASE：$59=(111011{)}_2$, $53=(110101{)}_2$
则$59\&53=(110001{)}_2=49=a$
而$59+53=112=s$
$s-2a=14=(001110{)}_2$
$s-2a\&a=(001110{)}_2\&(110001{)}_2=0$
得证！

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;

ll T, a, s;

int main()
{
    cin >> T;
    while (T--)
    {
        cin >> a >> s;
        if (s - 2 * a >= 0)
        {
            ll t = s - 2 * a;
            if ((t & a) == 0)
            {
                puts("Yes");
                continue;
            }
        }
        puts("No");
    }
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

E - Range Sums

题目描述

翻译：给定$N$个区间的区间和，最后是否能够得出$a_1+a_1+\cdot \cdot \cdot a_n$的值？

解题思路

对于给出的一组区间[l,r]表示为$a_l+a_{l+1}+\cdot \cdot \cdot +a_r$,可以转换为前缀和$b_r-b_{l-1}$
举例：第一次给出[3,6]即$a_1+a_2+a_3$的值,我们可以将它转换为前缀和$b_6-b_2$

本题我们可以采用并查集来做，首先将所有的端点放入各自的集合
而对于每一个给出的区间，我们只需要将它的(右端点)和(左端点-1)合并，
如果最后查找$n$和$0$在一个集合内，说明可以求出$a_1+a_1+\cdot \cdot \cdot a_n$

问：为什么最后是判断$n$和$0$?

因为[1,n]的前缀和为b[n]-b[1-1]= b[n]-b[0],并查集中存的是前缀和区间

问：为什么可以用并查集做？

因为对于每个给出的区间，其实是给出了某段区间的左右端点，而一开始每个点都是零散的集合
用并查集的目的就是把某些端点连接起来，使得最后0和n两个端点能够连接，即在一个集合内

问：如果给出n = 4, m = 2, c = {[1,3], [2,4]} 这一组数据，能否输出“Yes”?

不能，因为给出这两个区间只能算出[1,3],[2,4]两个区间和，不管两个区间和如何加减乘除都算不出[1,4];
要算出[1,4]需要额外的区间信息如[3,4]或[1,2]或{[1,1],[2,2]}或{[3,3],[4,4]等};

代码

#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;

int n, m, l, r;
int fa[N];

int find(int x)
{
    if (x != fa[x]) fa[x] = find(fa[x]);
    return fa[x];
}

int main() 
{
    cin >> n >> m;
    for (int i = 0; i < N; i++) fa[i] = i;  // 初始化

    while (m--)
    {
        cin >> l >> r;
        fa[find(l - 1)] = find(r); 
    }

    if (find(0) == find(n)) puts("Yes");
    else puts("No");
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28