如何产生指定分布的随机数？_怎么根据一个分布求随机变量

参考：https://www.cnblogs.com/xingshansi/p/6539319.html；
　　　https://www.jianshu.com/p/3d30070932a8；
　　　https://blog.csdn.net/pipisorry/article/details/50615652；
　　　https://cosx.org/2015/06/generating-normal-distr-variates。

常用方法：逆变换法和舍选法

1、逆变换法（反演法）

对任意随机变量$\xi$，设其概率密度分布函数为$P(x)$，其积分分布函数为$P(x)=\int_{-\propto }^{x}p(z)dz$，只要有均匀分布的另一随机变量$\theta$，则反函数$\xi=F^{-1}(\theta)$即可得到，且$\xi$一定服从$P(x)$分布。

逆变换法产生随机数的步骤：
①生成一个服从均匀分布的随机数U~Unit(0,1);
②设F(x)为指定分布的分布函数，则X=F−1（U）X=F−1（U）即为指定分布的随机数。
示例：生成满足λ=2的指数分布随机数。
分析：由$f(x)$得出$F(x)$—>$F(x) = 1 - {e^{ - \lambda x}}$，进而求得$F(x)$逆函数，得出$X = {F^{ - 1}}(u) = - \frac{1}{\lambda }\ln (1 - u)$
代码：

Len = 1000000;
u = rand(1,Len);
lemda = 2;
x = -1/lemda*(log(1-u));
1
2
3
4

常见分布的生成函数：
(1)瑞利分布

$$F_r(x)={\displaystyle 1-e^{-x^{2}/\left(2\sigma ^{2}\right)}}$$ $$\Rightarrow x=\sqrt{-2\sigma^2ln(1-\mu)}$$

(2)威布尔分布

$$F_w(x)= 1- e^{-(x/\lambda)^k}$$ $$\Rightarrow x=\lambda [-ln(1-\mu)]^{1/k}$$

(3)对数正态分布
　　由于对数正态分布的累积分布函数不存在解析式，因此不能直接给出其生成函数。若x服从对数正态分布，则有y=ln x服从正态分布。根据这一思想，对应的随机序列仿真步骤如下：
步骤1：生成高斯序列$y\sim N(\mu,\sigma^2)$。
步骤2：用$x=F^{-1}(y)=exp(y)$即可得到对数正态分布序列。

(4)K分布
　　由于K分布的累积分布函数没有解析式，故不能采用逆变换法生成随机数。由于K分布把杂波看作是功率收一随机过程调制的复高斯过程，可以用两个独立的、具有不同相关时间随机变量的乘积形式来描述其幅度统计特性。K分布随机序列可通过以下两步得到：
步骤1：生成瑞利分布序列G(n)和伽马分布随机序列S(n)；
步骤2：利用公式$z(n)=\sqrt{S(n)}G(n)$生成K分布序列。

2、舍选法

舍选法基本思想是利用拒绝采样，通过设定一个程序可抽样的分布q(x)比如正态分布等等，然后按照一定的方法拒绝某些样本，达到接近p(x)分布的目的。

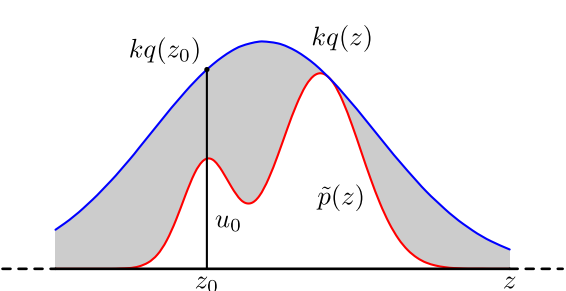
红色的是p(z), 蓝色的是q(z)，我们对q(z)乘一个参数k，让k能正好包住p(z)，那么对于每一个从q(z)得到的样本z0，我们有一定的概率接受它，概率的大小就是p(z0) / kq(z0)。很容易就能看出来，在p(z)和kq(z)相切的地方的采样，接受率就是1。那么有人问了，接受率能计算出来，但是我们对于一个样本z0，到底怎么判断是接受还是不接受啊？我们有u~Uniform[0,1]，对于每一个样本z0，我们一个u0，如果u0 <= p(z0) / kq(z0)，我们就接受，否则就拒绝。重复此过程，得到的样本就服从分布p(z)。
步骤：
①产生样本$z_0∈q(z)$和$u_0∈uniform[0,1]$
②若$u_0≤p(z_0)/kq(z_0)$，则接受$z_0$
③重复上述过程
④接受的样本服从$p(z)$分布
例子：对截断正态分布采样如下图

程序：

clear
k = normpdf(4.0/3,1,1)/normpdf(4.0/3,0,2);
N = 50000;
a = [];
for i=1:N
    accept = 0;
    while accept==0
        u = rand();
        z = normrnd(0,2); %产生随机数，满足正态分布
        %判定条件
        if z<=4 && z>=0 && u<=normpdf(z,1,1)/(k*normpdf(z,0,2))
            accept = 1;
            a = [a;z];
        end
    end
end
%显示结果
hist(a,5000)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

结果：