动态规划（备战蓝桥）刷题

背包

背包最基础版

#include <bits/stdc++.h>  
  
using namespace std;  
  
const int N = 1e3 + 10;  
  
int f[N]; // f[j] 表示总体积不超过j时的最大值  
  
// 注意：这里已经优化为了一维数组，f[j] 表示的是从前i个物品中选择总体积不超过j时的最大值  
  
int n, m;  
  
int w[N], v[N]; // w[i] 表示第i个物品的体积，v[i] 表示第i个物品的价值  
  
int main()  
{  
    cin >> n >> m; // n 是物品数量，m 是背包的总容量  
  
    for (int i = 1; i <= n; i++)  
        cin >> w[i] >> v[i]; // 输入每个物品的体积和价值  
  
    // 初始化f数组，表示在不选择任何物品时，背包容量为j时的最大价值为0  
    // 但由于这里是动态更新，且从后往前更新，实际上不需要显式初始化  
  
    // 动态规划过程  
    for (int i = 1; i <= n; i++) // 遍历每个物品  
    {  
        for (int j = m; j >= w[i]; j--) // 从背包容量m开始向前遍历，直到可以放下当前物品w[i]  
        {  
            // 关键步骤：更新f[j]的值  
            // f[j] 要么保持不变（即不选择当前物品i），要么更新为选择物品i后的新值（f[j-w[i]] + v[i]）  
            // 由于是从后往前更新，f[j-w[i]] 保存的是选择物品i之前的状态  
            f[j] = max(f[j-w[i]] + v[i], f[j]); // 更新f[j]的值  
        }  
    }  
  
    cout << f[m]; // 输出背包容量为m时的最大价值  
  
    return 0;  
}

背包加强（增加物品个数）

#include <iostream>  
using namespace std;  
  
const int N = 1010;  
int n, m; // n 表示物品数量，m 表示背包的总容量  
int v[N], w[N], s[N]; // v[i] 表示第 i 个物品的体积，w[i] 表示第 i 个物品的价值，s[i] 表示第 i 个物品的最大数量  
int f[N]; // f[j] 表示背包容量为 j 时的最大价值  
  
int main() {  
    cin >> n >> m;  
    for (int i = 1; i <= n; i++) {  
        cin >> v[i] >> w[i] >> s[i];  
    }  
  
    // 动态规划的主循环  
    for (int i = 1; i <= n; i++) { // 遍历每个物品  
        for (int j = 1; j <= m; j++) { // 遍历背包的容量  
            for (int k = 0; k <= s[i] && k * v[i] <= j; k++) { // 遍历当前物品的最大数量以及当前背包容量是否足够  
                // 更新背包容量为 j 时的最大价值  
                // 如果选择 k 个第 i 个物品，则背包剩余容量为 j - k * v[i]  
                // f[j - k * v[i]] + k * w[i] 表示选择 k 个第 i 个物品后的总价值  
                f[j] = max(f[j], f[j - k * v[i]] + k * w[i]);  
            }  
        }  
    }  
  
    // 输出背包容量为 m 时的最大价值  
    cout << f[m] << endl;  
    return 0;  
}

背包之无限物品

#include <bits/stdc++.h>  
using namespace std;  
const int N = 1e3 + 10;  
int f[N]; // f[j] 表示总体积不超过j时的最大价值  
int n, m;

int w[N], v[N]; // w[i] 表示第i个物品的体积，v[i] 表示第i个物品的价值  
  
int main()  
{  
    cin >> n >> m; // n 是物品数量，m 是背包的总容量  
  
    for (int i = 1; i <= n; i++)  
        cin >> w[i] >> v[i]; // 输入每个物品的体积和价值  
  
    // 初始化f数组，f[0]初始化为0，其他f[j]初始化为负无穷（但在本题中，由于不选择任何物品时价值为0，默认即可）  
  
    // 动态规划过程  
    for (int i = 1; i <= n; i++) // 遍历每个物品  
    {  
        for (int j = w[i]; j <= m; j++) // 从当前物品的体积开始向前遍历到m  
        {  
            // 关键步骤：更新f[j]的值  
            // 可以选择0个或多个当前物品i，因此直接取f[j]和f[j-w[i]]+v[i]中的较大值  
            f[j] = max(f[j], f[j - w[i]] + v[i]);  
        }  
    }  
  
    cout << f[m]; // 输出背包容量为m时的最大价值  
  
    return 0;  
}

注意此代码与基础版本，在内层物品体积循环种存在区别，由于物品无限，则不需要担心遍历总体积从左到右造成的状态重叠，只要保证总的体积小于总体积即可。

2022(十三蓝桥杯届国赛大学B组真题第三题）

        

#include <bits/stdc++.h>  
using namespace std;  
typedef long long ll;

const int N = 2050;  
int n = 2022;  
ll f[N][11][N];  
// f[i][j][k] 表示从0到i中选择j个数，使得这j个数的和为k的方案数  
  
int main() {  
    // 初始化：对于任意i，如果不选择任何数（即j=0），那么和为0的方案数只有1种  
    for (int i = 0; i <= n; i++) {  
        f[i][0][0] = 1;  
    }  
  
    // 动态规划过程  
    for (int i = 1; i <= n; i++) {  
        // 遍历选择的数的个数j  
        for (int j = 1; j <= 10; j++) {  
            // 遍历可能的和k  
            for (int k = 0; k <= n; k++) {  
                // 如果不选择第i个数  
                // 那么方案数等于从0到i-1中选择j个数，和为k的方案数  
                f[i][j][k] = f[i-1][j][k];  
  
                // 如果k大于等于i，则可以选择第i个数  
                // 此时，方案数等于从0到i-1中选择j-1个数，和为k-i的方案数  
                // 加上原本不选第i个数的方案数（即f[i][j][k]的初值）  
                if (k >= i) {  
                    f[i][j][k] += f[i-1][j-1][k-i];  
                }  
            }  
        }  
    }  
  
    // 输出从0到n中选择10个数，使得这10个数的和为n的方案数  
    cout << f[n][10][n];  
  
    return 0;  
}

优化

#include <bits/stdc++.h>  
using namespace std;  
typedef long long ll;  
const int N = 2050;  
int n = 2022;  
ll f[11][N]; // f[j][k] 表示选j个数之和为k的方案数  
  
int main() {  
    f[0][0] = 1; // 初始化，没有选任何数时，和为0的方案数只有一种（即不选）  
  
    for (int i = 1; i <= n; i++) { // 遍历从1到n的所有数  
        for (int j = 10; j >= 1; j--) { // 遍历从10到1的所有可能选择的数的个数  
            for (int k = n; k >= i; k--) { // 遍历从n到i的所有可能的和  
                // 更新方案数：当前数i可以选择（即f[j-1][k-i]），也可以选择不选（即f[j][k]保留原有值）  
                // 由于j和k是倒序遍历的，所以f[j-1][k-i]表示的是上一轮（即i-1）时的状态，不会被当前轮次影响  
                f[j][k] += f[j-1][k-i]; // 加上选择数i的方案数  
            }  
        }  
    }  
    cout << f[10][n]; // 输出选10个数之和为n的方案数  
    return 0;  
}

状态转移

路径转移

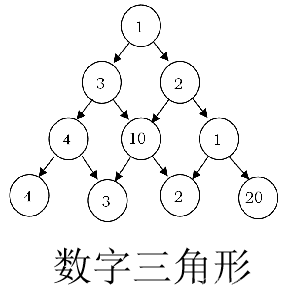
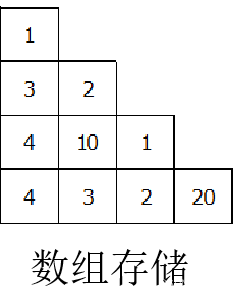
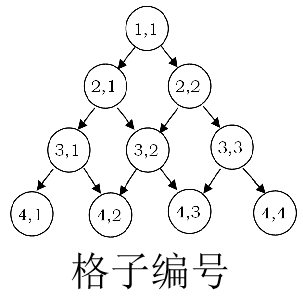
数字三角形

（给出一个全部由正数构成的数字三角形，从第一行走到最后一行，每次只能往正下或者正右下走。每次累积经过的数，要求和最大。）

#include <bits/stdc++.h>  
using namespace std;  
#define N 103  
  
int map[N][N];  // 存储输入数据的二维数组  
int fp[N][N];  // 动态规划数组，用于存储到达当前位置的最大路径和  
  
int main()  
{  
    int n, maxy;  
    cin >> n;  // 输入三角形的行数  
  
    // 读取三角形的每一行数据  
    for(int i = 1; i <= n; i++)  
    {  
        for(int j = 1; j <= i; j++)  
        {  
            cin >> map[i][j];  // 读取第i行第j个元素  
        }  
    }  
  
    // 动态规划计算到达每个位置的最大路径和  
    for(int i = 1; i <= n; i++)  
    {  
        for(int j = 1; j <= i; j++)  
        {  
            // 如果当前位置是第一列，那么只能从上方过来  
            // 否则，比较从右上方和左上方过来的路径和，取较大的那个加上当前值为当前最大
              fp[i][j]=max(fp[i-1][j],fp[i-1][j-1])+map[i][j];
        }  
    }  
  
    // 在最后一行找到最大的路径和  
    for(int i = 1; i <= n; i++)  
        maxy = max(maxy, fp[n][i]);  
  
    cout << maxy;  // 输出最大路径和  
    return 0;  
}

洛谷 P1004 方格取数 （两路径求最大）

#include <bits/stdc++.h> 
using namespace std;  
  
// 定义二维数组mp用于存储地图上的值  
int mp[11][11];  
// 定义四维数组f用于存储动态规划的结果，f[i][j][l][k]表示从(1,1)到(i,j)和(l,k)的最大路径和  
int f[11][11][11][11];  
  
int main()  
{  
    int n;  
    cin >> n; // 读取地图的大小n  
  
    int a, b, c;  
    while(1)  
    {  
        cin >> a >> b >> c;  
        if(a == 0 && b == 0 && c == 0) break; // 如果输入是0 0 0，则结束输入  
        mp[a][b] = c; // 将地图上的值存储到mp数组中  
    }  
  
    int i, j, l, k;  
    for(i = 1; i <= n; i++)  
        for(j = 1; j <= n; j++)  
            for(l = 1; l <= n; l++)  
                for(k = 1; k <= n; k++)  
                {  
                    // f[i][j][l][k]的值取决于四个方向上的最大值，并加上当前位置的值mp[i][j]  
                    f[i][j][l][k] = max(max(f[i - 1][j][l - 1][k], f[i][j - 1][l][k-1]),   
                                        max(f[i - 1][j][l][k - 1], f[i][j - 1][l - 1][k])) + mp[i][j];  
  
            // 相同位置的数只能加一次 ，如果(i,j)和(l,k)不是同一个位置，则再追加上(l,k)位置的值
                    if(i != l && j != k) f[i][j][l][k] += mp[l][k];  
                }  
  
    // 输出从(1,1)到(n,n)的两个路径的最大和  
    cout << f[n][n][n][n];  
  
    return 0;  
}

洛谷 P1006 传纸条 （两路径不能相交求最大）

#include <bits/stdc++.h>  
using namespace std;  
const int N = 52;  
int mp[N][N];  
// f[i][j][l][k] 表示从 (1,1) 到 (i,j) 和从 (1,1) 到 (l,k) 两条路径总和的最大值 
// 注意到由于不相交的限制，( i , l )!=( j , k )
int f[N][N][N][N];  

int main()  
{  
    int m, n;  
    cin >> m >> n; // 读取矩阵的行数和列数  
  
    // 读取矩阵元素  
    for(int i = 1; i <= m; i++)  
    {  
        for(int j = 1; j <= n; j++)  
        {  
            cin >> mp[i][j];  
        }  
    }  
  
    // 初始化动态规划数组（这里默认初始化为0，因为未访问的元素默认为0）  
  
    // 动态规划计算两条不相交路径的最大和  
    for(int i = 1; i <= m; i++)  
    {  
        for(int j = 1; j <= n; j++)  
        {  
            for(int l = 1; l <= m; l++)  
            {  
                for(int k = 1; k <= n; k++)  
                {  
                    //两条路径不能经过相同的点 
                    if(i != l && j != k)  
                    {  
                        //当前位置的值是由上和左边的点转移而来
                       // f[i][j][l][k]的值取决于四个方向上的最大值并加上当前位置 (i,j) 和 (l,k) 的元素值
                        f[i][j][l][k] = max( 
                                max(f[i-1][j][l-1][k], f[i-1][j][l][k-1]), 
                                max(f[i][j-1][l-1][k], f[i][j-1][l][k-1]))
                            + mp[i][j] + mp[l][k]; // 加上当前两个位置的元素值  
                    }  
                }  
            }  
        }  
    }  
      
    // 输出从 (1,1) 到 (m-1,n) 和从 (1,1) 到 (m,n-1) 的两个不相交路径的最大和  
    // 最后一个重合点是转移不了的，不能直接输出，但它由只能由左和上方得来 
    //不论哪条路的终点在哪，结果都是一样的 
    cout << f[m-1][n][m][n-1] << endl;  //cout << f[m][n-1][m-1][n] << endl; 
  
    return 0;  
}

序列转移

最长上升子序列（LIS）

蓝桥勇士 时间复杂度O(n^2)

#include <bits/stdc++.h>   
using namespace std;  
const int N = 1e3 + 7;  
int a[N];  
// 动态规划数组，dp[i]表示以a[i]为结尾的最长递增子序列的长度  
int dp[N];  
  
int main()  
{  
  int n;  
  cin >> n; 
  for(int i = 0; i < n; i++) cin >> a[i];  
  
  // 初始化dp数组，每个元素的最长递增子序列长度至少为1（自己本身）  
  for(int i = 0; i < n; i++)  
  {  
    dp[i] = 1; // 最开始每个元素都构成了一个长度为1的递增子序列  
  
    // 对于每个元素a[i]，遍历它之前的所有元素a[j]（j < i）  
    for(int j = 0; j < i; j++)  
    {  
      // 如果当前元素a[i]大于之前的元素a[j]，则可以尝试将a[i]加入到以a[j]为结尾的递增子序列中  
      if(a[i] > a[j])   
      {  
        // 更新dp[i]，取之前的最大长度dp[j]加1和当前dp[i]的较大值  
        dp[i] = max(dp[i], dp[j] + 1);  
      }  
    }  
  }  
  // 找出dp数组中的最大值，即最长递增子序列的长度  
  int m = 0;  
  for(int i = 0; i < n; i++)  
  {  
    if(dp[i] > m) m = dp[i];  
  }  

  cout << m;  
  
  return 0;  
}

蓝桥骑士 时间复杂度为O(n * log n)

贪心加动态规划，题目与上题完全相同，但能通过N≤3×10^5的数据

#include <bits/stdc++.h>
using namespace std;  
const int N = 3e5 + 7; 
int a[N], b[N]; // a数组用于存储原始数据，b数组用于存储最长递增子序列  
  
int main()  
{  
  int n;  
  cin >> n;
  int len = 0; // 初始化最长递增子序列的长度为0  
  
  // 读取序列的元素到数组a中，注意数组索引从1开始 
  for(int i = 1; i <= n; i++) cin >> a[i];  
  // b数组的第一个元素就是a数组的第一个元素，此时len为1  
  b[++len] = a[1];  
  
  // 遍历数组a的剩余元素  
  for(int i = 2; i <= n; i++)  
  {  
    // 如果当前元素a[i]大于b数组的最后一个元素（即当前最长递增子序列的末尾）  
    // 则直接将其加入到b数组的末尾，并更新len  
    if(a[i] > b[len]) b[++len] = a[i];  
    else  
    {  
      // 否则，在b数组中找到第一个大于或等于a[i]的元素的位置  
      // lower_bound函数返回的是指向该位置的地址 
      // 通过减去b数组首地址，我们将其转换为索引值  
      int pos = lower_bound(b + 1, b + len + 1, a[i]) - b;  
      // 更新b数组中该位置的元素为a[i]（保持递增性，同时替换更小的元素）  
      b[pos] = a[i];  
    }  
  }  
  // 输出最长递增子序列的长度  
  cout << len;  
  return 0;  
} 

注：此方法只是贪心的求出最长的子序列，但并不保证所得到的序列是合法子序列

它通过不断修改b中大的值使其接受更多后面的值。

最长公共子序列（LCS）

#include <bits/stdc++.h>  
using namespace std;   
const int N = 1e3 + 7;  
// 存储两个序列的数组  
long long a[N], b[N];  
  
// 二维动态规划数组，dp[i][j]表示a的前i个元素和b的前j个元素的最长公共子序列的长度  
long long dp[N][N];  
  
int main()  
{  
    int n, m;  
    cin >> n >> m; 
    for (int i = 1; i <= n; i++) cin >> a[i];   
    for (int i = 1; i <= m; i++) cin >> b[i];  
  
    // 动态规划填充dp数组  
    // 初始化边界条件（当其中一个序列为空时，LCS的长度为0）  
    // 在此程序中，边界条件已经被数组的默认初始化（0）所满足  
  
    // 遍历两个序列的所有子序列组合  
    for (int i = 1; i <= n; i++)  
    {  
        for (int j = 1; j <= m; j++)  
        {  
            // 如果当前元素相等，则LCS长度增加1，并继承前一个位置的状态  
            if (a[i] == b[j])  
                dp[i][j] = dp[i-1][j-1] + 1;  
            // 如果当前元素不相等，则LCS长度不增加，在另外两种状态中求最大 
            else  
                dp[i][j] = max(dp[i][j-1], dp[i-1][j]);  
        }  
    }  
  
    // 输出整个序列a和序列b的LCS长度  
    cout << dp[n][m];  
    return 0;  
}

接龙数列（14届省赛）

#include <bits/stdc++.h>  
using namespace std;  
// 一共就（0-9）十个数字 
int N, dp[10];  //dp[i]表示以数字i结尾的最长递增子序列的长度
int main()  
{  
  cin >> N; // 读取数字序列的长度  
  
  for(int i = 0; i < N; i++)  
  {  
    int a;  
    cin >> a; // 读取一个数字  
  
    vector<int> s; // 创建一个空vector，用于存储数字的每一位  
  
    // 将数字a的每一位拆分并存储到vector s中  
    while(a)  
    {  
      s.push_back(a % 10);  
      a /= 10;  
    }  
  
    // 获取数字a的个位和最高位 
    int x = s.back(); // 个位  
    int y = s.front(); // 最高位  
  
    // 更新dp数组，尝试以y结尾的最长递增子序列  
    // 如果x可以接在y后面形成递增子序列，则更新dp[y]  
    dp[y] = max(dp[y], dp[x] + 1);  
  }  
  int res = 0; // 用来存储最长递增子序列的长度  
  
  // 遍历dp数组，找到最长的递增子序列  
  for(int i = 0; i < 10; i++)  
    res = max(res, dp[i]);  
  
  //N减去最长递增子序列的长度 ，即是最少需要删去的元素 
  cout << N - res;  
  return 0;  
} 

动态规划加优化

统计子矩阵（十三届省赛大学B组真题）

#include <iostream>  
using namespace std;  
typedef long long ll;  
ll k;  
int n,m;  
const int N=507;  
int a[N][N];  
// 定义一个二维数组sum，用于存储矩阵的前缀和  
ll sum[N][N];  
  
int main()  
{  
  // 输入矩阵的行数n和列数m  
  cin>>n>>m;  
  // 输入给定的阈值k  
  cin>>k;  
  
  // 读取矩阵的值，并同时计算前缀和  
  for(int i=1;i<=n;i++)  
  {  
    for(int j=1;j<=m;j++)  
    {  
      cin>>a[i][j];  
      // 计算当前位置(i,j)的前缀和  
      sum[i][j]=a[i][j]+sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1];  
    }  
  }  
  
  ll cnt=0;  
  // 遍历矩阵的每一行作为子矩阵的起始行  
  for(int i=1;i<=n;i++)  
  {  
    // 遍历矩阵的每一行作为子矩阵的结束行（起始行之后的所有行）  
    for(int j=i;j<=n;j++)  
    {  
      // 初始化列指针l和r  
      int l=1,r=1;  
      // 遍历矩阵的每一列作为子矩阵的结束列  
      for(r=1;r<=m;r++)  
      {  
        // 当子矩阵的和超过阈值k时，移动左边界l  
        while(l<=r && sum[j][r]-sum[j][l-1]-sum[i-1][r]+sum[i-1][l-1]>k) l++;  
        // 将以当前右边界r为结束的所有可能的子矩阵的数量加到cnt上  
        cnt=cnt+r-l+1;    
      }  
    }  
  }  

  cout<<cnt;  
  return 0;  
}

树上dp+dfs=最近公共祖先（板子）较难理解，可以先背

在接下来的3题中int fa[N][20];代表N这个节点第2^i个父亲是谁，（比如x=fa[1][0]意味着1号节点的父节点被赋值给了x。）那么就有n的第2^i个父亲就是n的2^(i-1)个父亲的第2^(i-1)个父亲，

即fa[u][i] = fa[fa[u][i - 1]][i - 1];

机房（十三届国赛大学B组真题）

#include <iostream>  
#include <vector>  
#include <cmath> // 用于log2函数的定义  
using namespace std;  
  
// 设定一个大的常数N，作为节点数量的上限  
const int N = 1e6 + 10;  
  
// 图的邻接表表示  
vector<int> g[N << 1]; // 使用两倍空间，因为是无向图  
  
// 用于存储节点u到根节点的路径上的权值和  
int sum[N];  
// 节点的权值（在这里假设节点的权值就是它的度数）  
int a[N];  
// 节点的深度  
int dep[N];  
// 节点u的2^i级祖先  
int fa[N][20];  
// 节点数量n和查询数量m  
int n, m;  
  
// 深度优先搜索函数，用于初始化深度、祖先和路径权值和  
void dfs(int u, int fath) {  
    dep[u] = dep[fath] + 1; // 更新节点u的深度  
    fa[u][0] = fath; // 初始化节点u的0级祖先为其父节点  
  
    // 预处理fa数组，计算每个节点的2^i级祖先  
    for (int i = 1; (1 << i) <= dep[u]; i++) {  
        fa[u][i] = fa[fa[u][i - 1]][i - 1];  
    }  
  
    // 遍历节点u的所有邻居  
    for (int i = 0; i < g[u].size(); i++) {  
        int v = g[u][i];  
        // 如果v是u的父节点，则跳过 因为要保证查找的顺序从上到下不重复
        if (v == fath) continue;  
        // 更新节点v的路径权值和（假设节点的权值为其度数）  
        sum[v] = sum[u] + a[v];  
        // 递归遍历节点v的子树  
        dfs(v, u);  
    }  
}  
  
// 查找节点x和节点y的最近公共祖先  
int lca(int x, int y) {  
    // 将x和y调整到同一深度，深度大的节点向上跳跃  
    if (dep[x] < dep[y]) swap(x, y);  
    int d = dep[x] - dep[y];  
    // 向上跳跃到同一深度  
    for (int i = 0; i <= log2(n); i++) {  
        if ((1 << i) & d) x = fa[x][i];  
    }  
  
    // 如果x和y已经是同一个节点，则返回x（或y）  
    if (x == y) return x;  
  
    // 从上到下比较x和y的祖先，直到找到最近的公共祖先  
    for (int i = log2(n); i >= 0; i--) {  
        if (fa[x][i] != fa[y][i]) {  
            x = fa[x][i];  
            y = fa[y][i];  
        }  
    }  
  
    // 最后的fa[x][0]即为x和y的最近公共祖先  
    return fa[x][0];  
}  
  
// 主函数  
signed main() {  
    cin >> n >> m;  
  
    // 读取边和构建图  
    for (int i = 1, u, v; i < n; i++) {  
        cin >> u >> v;  
        g[u].push_back(v);  
        g[v].push_back(u);  
    }  
  
    // 假设每个节点的权值就是它的度数（即连接的边的数量）  
    for (int i = 1; i <= n; i++) {  
        a[i] = g[i].size(); // 节点的权值  
        sum[i] = g[i].size(); // 初始化sum[i]为节点的度数（用于后续计算）  
    }  
  
    // 深度优先搜索，初始化深度、祖先和路径权值和  
    dfs(1, 0);  
  
    // 处理m个查询  
    for (int i = 1; i <= m; i++) {  
        int u, v;  
        cin >> u >> v;  
  
        // 计算u和v之间路径上的权值和（包括u和v，但不包括它们的最近公共祖先）

        cout<<sum[u]+sum[v]-2*sum[lca(u,v)]+a[lca(u,v)]<<endl;
        }
}

景区导游（十四届省赛大学B组真题）

//本题主要考察LCA

//若要求u->v的路径长度,等于求u->root+v->root - root->2*LCA(u,v)

//即分别从u和v走到根结点,再减去2倍的根结点到(u,v)的最近公共祖先的路径长度

//同理,若原本的遍历顺序是a->b->c,总路径长度为sum,若要跳过b,则新的路径长度为

//sum-dist(a,b)-dist(b,c)+dist(a,c),可画图验证 

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;

const int N=1e5+100;

int n,k;

int dep[N];//深度 

int fa[N][21];//dp[i][j]表示从i结点开始跳2^j步可到达的结点 

vector<int>edge[N];//边 

vector<int>weight[N];//权值 

ll path[N];//原始的游览路线 

ll dist[N];//dist[i]存储i到根结点的距离 

void dfs(int u,int fath)

{

  dep[u]=dep[fath]+1;

  fa[u][0]=fath;

  for(int i=1;(1<<i)<=dep[u];i++)

    fa[u][i]=fa[fa[u][i-1]][i-1];

  for(int i=0;i<edge[u].size();i++)

  {

    int v=edge[u][i],w=weight[u][i];

    if(v==fath)

      continue;

    dist[v]=dist[u]+w;

    dfs(v,u);

  }

}

int lca(int x,int y)

{

  if(dep[x]<dep[y])

    swap(x,y);

  int d=dep[x]-dep[y];

  for(int i=0;i<=log2(n);i++)

    if((1<<i)&d)

      x=fa[x][i];

  if(x==y)

    return x;

  for(int i=log2(n);i>=0;i--)

  {

    if(fa[x][i]!=fa[y][i])

      x=fa[x][i],y=fa[y][i];

  }

return fa[x][0];

}

ll get_dist(int x,int y)//求x和y的距离 

{

    if(x==0||y==0)return 0;

    return dist[x]+dist[y]-2*dist[lca(x,y)];     

}

int main()

{

    cin>>n>>k;

    for(int i=1;i<n;i++)//插入n-1条无向边 

    {

        int u,v,w;

        cin>>u>>v>>w;

        //储存双向边

        edge[u].push_back(v);

        edge[v].push_back(u);

        weight[u].push_back(w);

        weight[v].push_back(w);    

    }    

    dfs(1,0);//跑一遍dfs为LCA做准备 

    ll sum=0;//sum存储原始游览路线的总路径长度 

    for(int i=1;i<=k;i++)

    {

        cin>>path[i];

        sum+=get_dist(path[i],path[i-1]);//依次累加 

    }

    

    for(int i=1;i<=k;i++)//除去第i个景点 

    {

        ll dist1=get_dist(path[i],path[i-1]);

        ll dist2=get_dist(path[i],path[i+1]);

        ll dist3=get_dist(path[i-1],path[i+1]);

        cout<<sum-dist1-dist2+dist3<<' ';//套公式计算即可 

    }

  return 0;

}

砍树（十四届省赛大学B组真题）

#include <bits/stdc++.h>

using namespace std;

const int MAX_N=1e5+5;

vector <int> E[MAX_N],NUM[MAX_N];

int dep[MAX_N],fa[MAX_N][21],s[MAX_N];

int n,m,x,y,a,b,ans=-1;

void dfs(int u,int Fa){

    dep[u]=dep[Fa]+1;

    fa[u][0]=Fa;

    for(int i=1;i<=20;i++){

        fa[u][i]=fa[fa[u][i-1]][i-1];

    }

    for(int i=0;i<E[u].size();i++){

        int v=E[u][i];

        if(v==Fa) continue;

        dfs(v,u);    

    }

}

void dfs2(int u,int Fa){

    for(int i=0;i<E[u].size();i++){

        int v=E[u][i],p=NUM[u][i];

        if(v==Fa) continue;

        dfs2(v,u);

        s[u]+=s[v];

        if(s[v]==m) ans=max(ans,p);

    }

}

int lca(int x,int y)

{

  if(dep[x]<dep[y])

    swap(x,y);

  int d=dep[x]-dep[y];

  for(int i=0;i<=log2(n);i++)

    if((1<<i)&d)

      x=fa[x][i];

  if(x==y)

    return x;

  for(int i=log2(n);i>=0;i--)

  {

    if(fa[x][i]!=fa[y][i])

      x=fa[x][i],y=fa[y][i];

  }

  return fa[x][0];

}

int main(){

    cin>>n>>m;

    for(int i=1;i<n;i++){

        cin>>x>>y;

        E[x].push_back(y);

        NUM[x].push_back(i);

        E[y].push_back(x);

        NUM[y].push_back(i);

    }

    dfs(1,0);

    for(int i=1;i<=m;i++){

        cin>>a>>b;

        s[a]++;s[b]++;s[lca(a,b)]-=2;

    }

    dfs2(1,0);

    cout<<ans;

    return 0;

}

方案数dp

台阶方案（省模拟赛）

#include <iostream>

using namespace std;

typedef long long ll;

const ll mol=1000000007;

const int N=1e6+3;

int dp[N];//dp[i]表示走到第i的台阶的方案数

int a[3];//a[j]分别对应每次走的台阶数

int main()

{

  int n;

  cin>>n;

  for(int i=0;i<3;i++)

  {

    cin>>a[i];

  }

  dp[0]=1;//走到第0的台阶只有一种方案数

  //当前台阶可以通过三种走法过来

  for(int i=1;i<=n;i++)

  {

    for(int j=0;j<3;j++)//三种走法，每一种都可以试试能否转移

    {

      //一步的走台阶不能超过现在的台阶数i

      if(a[j]<=i)

      //总方案数等于三种的走法方案数的累加和

        dp[i]=(dp[i]%mol+dp[i-a[j]]%mol)%mol;

    }

  }

  cout<<dp[n];

  return 0;

}

李白打酒加强版（十三届省赛大学B组真题）

#include <bits/stdc++.h>

using namespace std;

using ll=long long;

const ll MOD=1000000007;

ll n,m,ans;

ll f[105][105][105];//i:店，j:花，k:酒

int main(){

  cin>>n>>m;

  f[0][0][2]=1;

  //状态由前往后转移

  for(int i=0;i<=n;i++){

      for(int j=0;j<=m;j++){

          for(int k=0;k<=m;k++){

              //当前状态遇到花 

              if(j&&k)//当前方案数加上在前一状态下的方案数

                f[i][j][k]=(f[i][j][k]+f[i][j-1][k+1])%MOD;//前一方案及在当前基础上花没遇到，酒也没喝

              //当前状态遇到店

              if(i&&k%2==0)

                f[i][j][k]=(f[i][j][k]+f[i-1][j][k/2])%MOD;//前一方案及在当前基础上店没遇到，酒也没加

            }

        }

    }

    //已知最后状态为：剩一斗酒，之前遇到m-1多花，和n个酒店的所有方案数

    cout<<f[n][m-1][1];

    return 0;

}

纸牌游戏（洛谷P10111）

#include<bits/stdc++.h>  

using namespace std;  

int n; // 游戏的轮数  

int a[1003], b[1003], c[1003]; // a[i] 表示第 i 轮出的牌的价值，b[i] 表示换牌的花费，c[i] 表示对手出的牌  

int dp[1003][1003][3]; // dp[i][j][k] 表示进行到第 i 轮，换了 j 次牌，当前出的牌为 k 的最大得分  

int ans; // 存储最大得分  

  

int main(){  

    cin >> n;  

      

    // 读取每轮自己出的牌的价值  

    for(int i = 1; i <= n; i++) cin >> a[i];

    // 读取每次换牌的花费  

    for(int i = 1; i < n; i++) cin >> b[i]; // 注意这里只需要 n-1 个换牌花费，因为最多换 n-1 次牌  

    // 读取对手每轮出的牌  

    for(int i = 1; i <= n; i++) cin >> c[i];  

  

    // 动态规划  

    for(int i = 1; i <= n; i++){ // 枚举轮数  

        for(int j = 0; j < i; j++){ // 枚举本轮换牌次数（到第 i 轮最多换了 i-1 次牌）  

            for(int k = 0; k < 3; k++){ // 枚举出的牌  

                int add = 0, tt = -2e9; // add 为本局得分，tt 为当前状态的最大得分  

  

                // 根据当前出的牌和对手出的牌计算得分  

                if((c[i] + 1) % 3 == k) add = (a[i] << 1); // 赢的情况  

                else if(c[i] == k) add = a[i]; // 平的情况  

  

                // 不换牌的情况  

                tt = max(tt, dp[i-1][j][k]); // 继承上一轮不换牌且出同样牌的最大得分  

  

                // 换牌的情况（注意：这里只能换前一次出的牌，所以 j > 0）  

                if(j > 0){  

                    // 枚举换哪张牌，由于牌只有三种，可以用 (k+1)%3 和 (k+2)%3 来表示  

                    tt = max(tt, max(dp[i-1][j-1][(k+1)%3], dp[i-1][j-1][(k+2)%3]) - b[j]);  

                }  

                // 更新 dp 数组  

                dp[i][j][k] = tt + add; // 加上这局的分  

            }  

        }  

    }  

  

    // 遍历最后一轮的所有状态，找到最大得分  

    for(int i = 0; i < n; i++){  

        ans = max({ans, dp[n][i][0], dp[n][i][1], dp[n][i][2]});  

    }  

  

    cout << ans; // 输出最大得分  

    return 0;  

}

01背包

费用报销（十三届国赛大学B组真题）

#include <iostream>

#include <algorithm>

using namespace std;

int N, M, K, cnt;

const int S = 5005;

int dp[S][S];

//预处理每一个月多少天

int month[12] = { 31,28,31,30,31,30,31,31,30,31,30 };

struct node

{

    int m;

    int d;

    int days;

    int v;

}Z[S];

bool cmp(node x,node y)

{

    if (x.m == y.m)

    {

      return(x.d < y.d);

    }

    return(x.m < y.m);

}//根据票据的时间进行排序，时间越早的越靠前

int main()

{

    cin >> N >> M >> K;

    for (int i = 1;i <= N;i++)

    {

      cin >> Z[i].m >> Z[i].d >> Z[i].v;

    }

    

    sort(Z + 1, Z + 1 + N, cmp);

    for (int i = 1;i <= N;i++)

    {

        for (int j = 0;j < Z[i].m - 1;j++)

        {

          Z[i].days += month[j];

        }

        Z[i].days += Z[i].d;

    }//将时间转化为天数

    for (int i = 1;i <= N;i++)//开始动态规划

    {

        for (int j = 1;j <= M;j++)

        {

            dp[i][j] = dp[i - 1][j];

            if (j >= Z[i].v)

            {

                for (int k = i - 1;k >= 1;k--)

                {

                    if (Z[i].days - Z[k].days >= K)

                    {

                        cnt = k;

                        break;

                    }

                }//往前找到最近的一张时间间隔为K的票据

                if (Z[i].v + dp[cnt][j - Z[i].v] <= j)//保证不会超过背包容量

                {

                    dp[i][j] = max(dp[i][j], Z[i].v + dp[cnt][j - Z[i].v]);

                    //dp[cnt][j - Z[i].v]为剩余背包容量容纳第cnt张票据及,第cnt张票据之前的票据的最优解

                }

            }

        }

    }

   cout << dp[N][M];

}

搬砖（十三届国赛大学

#include <iostream>   

#include <cstring>  

#include <algorithm>  

#define int long long  // 定义int为长整型  

using namespace std;  

  

// 设定砖块的最大数量  

const int N = 1010;  

// 设定背包的最大容量（即总重量）  

const int M = 20010;  

int n, m;  // n为砖块数量，m为总重量  

int f[M];  // f[j]表示容量为j的背包能装下的最大价值  

  

struct node {  

  int w, v;  // w:体积，即砖块的重量；v:价值，即砖块的价值  

} a[N];  

  

// 比较函数，按照砖块的价值与重量的和从小到大排序  

bool cmp(node a, node b) {  

  return a.v + a.w < b.v + b.w;  

}  

  

void solve() {  

  cin >> n;  

  for (int i = 1; i <= n; i++) {  

    cin >> a[i].w >> a[i].v;  

    m += a[i].w;  // 累加砖块的总重量  

  }  

  

  // 按照砖块的价值与重量的和进行排序  

  sort(a + 1, a + n + 1, cmp);  

  

  int ans = 0;  // 初始化最大价值为0  

  

  // 动态规划，从第一个砖块开始遍历  

  for (int i = 1; i <= n; i++) {  // 注意这里是从1开始，因为a数组是从1开始的  

    // 从最大容量m开始遍历，直到当前砖块的重量  

    for (int j = m; j >= a[i].w; j--) {  

      // 判断当前砖块是否能放入背包（即当前背包的剩余容量是否大于等于砖块的重量）  

      // 并且放入这个砖块后，剩余容量是否小于等于这个砖块的价值（这是题目的特殊要求）  

      if (j - a[i].w <= a[i].v) {  

        // 如果满足条件，则更新f[j]的值  

        f[j] = max(f[j], f[j - a[i].w] + a[i].v);  

      }  

      // 更新最大价值（注意这里只需要在遍历完所有可能的背包容量后更新一次即可）  

      ans = max(ans, f[j]);  

    }  

  }  

  // 输出最大价值  

  cout << ans;  

}  

  

signed main() {  //由于int被定义为long long所以只能用signed

  solve();  

  return 0;  

}

B组真题）