canvas计算角度_canvas 两个点角度

作者：小蓝xlanll | 2024-03-19 01:30:20
踩
canvas 两个点角度
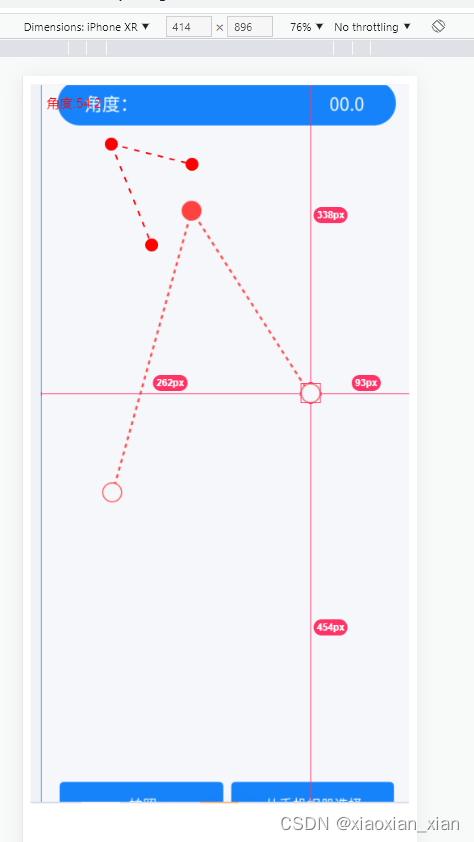
在这里插入图片描述
<!DOCTYPE html>
<html lang="en">
<head>
  <meta charset="UTF-8">
  <meta http-equiv="X-UA-Compatible" content="IE=edge">
  <meta name="viewport" content="width=device-width, initial-scale=1.0">
  <title>Document</title>
  <style>
    .btn {
      padding: 10px 20px;
      background: rgb(73, 152, 243);
      color: #fff;
      margin-top: 30px;
    }
  </style>
</head>
<body>
  <canvas id="myangle" style="width: 100%;" ref="canvass"></canvas>
  <script>
    var angle = '45°'
    var canwidth = 0
    var canheight = 0
    var cPointSize = 8
    var dragPoint = 0
    var point1 = { x: 100, y: 75 }
    var point2 = { x: 200, y: 100 }
    var point3 = { x: 150, y: 200 }
    var startX = 0
    var startY = 0
    var btnLoading = false
    var base64Img = 
    'data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAdUAAAN8CAYAAAAONTD4AAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAADsMAAA7DAcdvqGQAAGhYSURBVHhe7d2Hn1RXfqD9/SvW6/Xuer32er1er/2ux2N7PGN7ZjSAAsoBZQmUA8pZQlkClIUyCGWUJSRQAEkoICFEEIicc45Nx1tVN/ze87ulC0VxoOPpvlXn6c/nq6arTldXt+rWc/P9D8IHH3zwwQcffPTIx3/Y3dAoAACg+/7DnqZW6YxZGwsy5PNY2oKwV23bE8rXK0I5+81Q/sfIUP7jPQBQG64972t55cSXrffBnT8dEcoRY0OZuDCUzQ2hNLfZ+9KTch/VFvNH2NUUyoSFJek3JpQ/uc/+xwOAvCKqfeePTTP+flQoz88oycbdJqyt9tb0lNxHdYcJ6ls/hfJ3j4Xyn+61/9EAIM+Iat/6I9OO/zY8lEenhrJup701PSXXUd26J5QPzWK7BpUlVAC1iqj2vT8y/vqRUJ6aFsr6Xfbm9ITcRnV3cyhfLAvTVb76x7D9kQCgFhDV/PjVU6G8NDOUnU329nRXLqOq21FnrC3vlMQSKoBaR1TzQ7ex6s5LutDmYselXEZ1027zIpzAXr4A6gNRzZc/HR7K0S+Gsmp7eSHO1qGuyl1UW403fiwvotv+GABQa4hq/vz1w6E88FXPrwbOVVR1jmHtzpIMeD6U/3K//Q8BALWGqObPf74vlP/3eChz1oeyp8XepK7IVVR1jmHUt6V0Dy3bHwEAahFRzaf/Otz8v5kYypod9iZ1RW6iqgfkrtgWymGjzS/KUiqAOkJU80nPffCLUaFMXRlKYw8treYmqtsbQ3l9TnnOwfbL97U/MaF3ffIJPUBZV3vrZ9v9AGoTUc23EV+GsqGHjl3NTVSXbg1l8Nvl9dy2X7qvaOA09P2fD+V/PRTKHzsKngb7v48M5fCx5vMIwgrUE6Kab/q+O221vU2dlZuofm9+ob99LH8x0cN6Lno/ko17Ehk7K06fo21cd/3lg6HcMjmWpoLIhebn/fkD9nEAag9RzTd9/9UTQtja1Fm5iOqOxlBenpW/pVR9Pv/8VCgz1idSjETmbU7kk6WxjF+4v3fmx3LBe1F6bknb42T+p/kf9/89HsovnogO8M9PRXLKuMhENZEpKxM55uUDx2T+zyPlA5htPwNA/vRmVHXB5C8fCuW3z4Vy5AuR/Lv5rNE41Jnp9L3rH54I5Qgz/ogXynvFdmVTnL5n6s/u97z52S9G8utnyu97trF5os/7lk9D2dJgb1Rn5CKqK7eFcs0E+y/bV/QF+EsTsOd+iGVnq4npskRemxPLi7PLXjJeNV8v257Imt2JjJoWt3sY0PnvRvK2CfCn5rFsvlmdSFtJzM8T+X6dfYx68vs4faFy+kagNvRWVPVSZ/3HRvLCrFi+XpXI7I2JfGU+j5kZy2FjDpzx1/cQXft206eRfLQkllkbkvS952Pz70vGl2fgK8cfiq5dO+alSF4x74v6GPpYU1bG8th3sfzbs1Hu369OGxfKwk32RnVGLqI6a10oR5m5I9sv2hf0f76exP+uL2JZviORDxfHZq4vSi8fpEuaOhf3j09Gcu7bkSzcWl6yPNzM4dkeq9Lwr2JZawK8wHxPZSTnbErSx9EXf+Xt+rg/moli5a5Evlix73ZbVPXfujPVX5jb9dSOeX8BAz7pjajq0tY/PRWmcVzXkMhny8ubrD437x36vvP+wjhdGs3WcmXvGTd9GsuibYn8tDmRV34sLywsNe97umZON0VpqKt/VjXdJ0SXcvU9TDeVTTDvmc+aBZKpZkFhmXksDe1f6T4pP//sPPq3Z0OZsszeqM7IRVQ/XpSfMyjpi0N3SBr+dfmFudoETVfL/uOT5ZimTFz/3UT28xWxrDdjbvwkNku1++7/GzN3Z1sVrFHVOcehH0bpiytz2+RYnjdzkrprd+XtOpeoYdeJQlffZLfb9kLWnZs0/FdOjOXfzVxhRyYEAL2jN6KqM9o3fhKla7t0TZouBOh7hb43jZsbSyEUufajaO/qWI2wRnaVeY+btyWR094ovy/pGjfdnLXWvLd9sjQx783tLzDoUqoukW5pSuTxaXH6ta6G1iXU9xYksq1Z0sf8sxyfelYXmMb8YG9UZ+Qiqq/OLofI9ov2Jn0B6ovhGTOHpS+CRMpi858oPlBibrfdv3R7eZto9eNnUdUXtr7gM2/+FKdLqye+uv/tum3j3QWxtBQlPX5Xb9P/8Rr96sfWbSfzzYShP18f6w9j2p8QAPSO3ojq70dHMm1tIrtaJV1I0Wjq7fpZ49YYSLrkqDPfervG9fbPImkwt+vMexbb7HsmmiXeFTsTue7j9t9L+o8N5Yd15TVuGvFsxl8/n25ivamxvD/K/330wO/NC90WfNfn9kZ1Ri6i+vS0fJw8/y9MUHV1iS6hbtiTyGYz1/WdeZHq6pHMvVPidLWKzg0+bubMbjVLmdl9d5v7Zm4ov7COPURUs5+R0T1+zZ/BzOXJfrfrz28092m09UWpt+k2XN1+W/3YJ5gg6wSgkdef35HV0QB6R29E9ey3zHvAjkS+XZOkM97ZJiD9rGepm26ip5uzTnu9/N7wNyZwHy6K0/cZDV/14YK6Bk2XYl83M/2Vt9tcOSFKV/Pq5qnqK4vptlzd2XNrc5IuGVfelye6dm/oB/ZGdUYuovrQ1/m4xJuustVVvfd+GcvIr2NZYJb8Xv4xTudgMro3sMZUY6fh1FW02X26nVV3RNJtE4eK6t1mrvCyD6K9dAclffFW367B1qjrapsbPinfp4f36LaL6sfWOcBrzRylbje5wrzA9WTR1WMA9I3eiOrVE3X1q6Q7UlYvpOhSqO5oudXcf6l5H9HbdFOVrt1avC2Ro1488D1F3ws1lF+uTNpdbavviSvNTP0Tlhn+X5r3xY+WJBLGIoePjfYuQeeNrvo+5y17ozojF1EdPiUfO9boc9DtCX9m5lh0T13dSejNeXF6uEtmgHlRjJ4RS3NR5CwzZ/ibZ/bdp3vd6Zyfbp84VFQv/3D/+543S64/mDm5X5vHqrxdX/QadV39+7/biaSuZtEXvm771e2r2eoXAH3PdVQ1CMM+i2VHi8j95n1G3wMq79fNWg9NjdNVw9d9HKfvD7rUqEup+t6jq44rxytd26Wbkr43M/Y6036o92gNti4Y3DLpwKjqTp+6dk43l+l227zu76G/36DX7I3qjFxE9X4TVdsv2ZfOeTtKl1R1rzmdy8roHrlLtpeXHnU1y6dL992ne+jqjks653fQqG5I0iXOyts1qrp0q6twdWeljC6R6nGwHYkqgPxyHVUNlUZzu4mqhq06XDrDfad539bD9e77Mk6PQf0nMwNeCJN0O+u/Pnvg+9XvR5dXGeuCgK6hO9SJeT5dFstq816pa8mq79P9ZXQnJt2MddXEfJ/Y5pR6ierIL/O3ZKVR1ThqJDWWmXRV7c7yqgydw9NVI5X36bZPja4tqiNMVPXYrYvf3/8+XfLVOcg55sWrOxpkdOxG83h7AqIK1DLXUf1zE81Hv+1YVHXTlq4e1rVrGjpdODhUVOeapVU92uFQUdUjFHSfj/aiqkdK6JEM1WPyQH+/01+3N6ozchHVx7+1H4LSlzSqulSpq191o39Gdy/XHYWybaq6sT+7T48R07MrHWybqm530Bfpca/sf5+uEhlhXug6B6k7QmX0a1261c95XWUCoH2uo6qbrfR9oiNRveOz8olqdFPRnqC8MHCoqOrOl7qq+FCrf3WNmm5TbS+qukCRh51SbfRvcuF79kZ1Ri6iOnaG/TCRvjT4nSh9MT09ff9tBLrEqAHUpUd90enB09l9enDza3PjdM7OFlU9sFp3Oz/19Uh+NzqSgS9FcrShX+vPOxg9ycSxJsT6wiauQO1xHVVd03eziem25kQenhofsGORrnLVhYEdLYlc81GUjtdNTHo2OF0jZjsET08zqPuHfGeWZPW97VBR1TM46dEHemhO9X16GKCeUEK3qZ78WpTbK5Hp3+imT+yN6oxcRPW9eeX/wbZftK/oC09X4+qS55B3o7101/EPFiXSWjJzfObvcOF7++4bau7T7RN6xqTqqOqqhQmLy9svznyzvLPTx0vLOwno7uZ6SrHsjEmVdLWKxl330rvHLL3mbeYDQPtcR1Xpvhp6KOBb88onX6i8T49O0KVJvV9PwqC3/d1j5WNLdQnTdly9ztBrKCcvT9KluOr7K91vlpL1cTSu1ff96ukoPQxR90P512dDZ1f66q50iXqqvVGdkYuofrOifHFy2y/aFzSAutFft4/qGZVmmKhldNWuvjBLUfl4UJ3Ly+6ba+7bbuYEbdtUdQlTt5PqC1R3QDrDhFX3Ah6/sPwz9IwnN39qwmxuy1z/cSSPfBunc5PrGiQ9Du1/HGQjv85F6q7qumpFPx9qrhJA7+qNqOpSoO4HojPgGohsPxX9rAHV+/Q96/ifNz/psau69kyXXvVoh8olSP0efe/R96bqtXV6X3UYdXOZvu/pUq2+B2XbX/WzHq6jCxp6eI6ewKby+/Lkn58M5f359kZ1Ri6iumhzKOe+VbL+on1BA6jHm+ou4rqq9+qP9tEDonUJMjBLqg99E6e7p2f36XGl2VlFKqOqL0I9y4geoqOrhyt3OtJVwLpHsQZXVwPrC1LnCnWXeN3NXV/0etC07i6vE0H2fdV0m/S/PBWlc6G6A0JeV7EAPuqNqOoS4STz3qRHC+gxptl1mXVV8BlvROmSoh6l8E/m/UHH63vN5Wbpdkdr+dhWXVuo71VKj3PXNWh6djhdYs1+hh66o8fm6/4jldtGf/NMeWclXbLVaOt7WPqzzXO4akIku1qTdBVwno+fH/hiKDPX2hvVGbmI6qbdoTz8tf0X7Qt6Gi9dLasvUJ3D0xdIRq/o8KCJqW5T7f98+VyW2X16LJeefaR6m6q+EE8yc5E6J6dLwPp1dp8uVeq2Cz2+VU+N+NyMOB2rq3p1qXiJmbu8wiy16gtYX+zZ91XT42d113c905OGXbfZ2sYB6H29EVVdGNAlxuZikgZR14jpbQPN+4uuSWsxt+uZk/705xlufT/Rk0Losah6EnzdHqqrjfU2PYmD7vT02tzyMarZz/j7UZFMXKxX5iofmpPdru9/t5su6DZdPam+Hq6jM/p6LL++L21qlHQBIs8z+5eND2XtDnujOiMXUW1qDeWLZeUNxXlYbal7yemqCt3gX32mp67sqKRjdJuDrgK5csKB2xx0D2JdHazHvDa0iaw3L3B9QWvYdZuthr0yxDZ6jKs+5+Tn0xTazroEoG/0RlQ1khrAp6aXT2yvq251la8eP6qbsnQPXF3KrJw513/rUm0WVp3xV7qXsK49022tle9xemiNbvLS9z/ddJXdru/bujfxG2ahQlcn6+kQ9WfrpjL9t+5/ooE/1IJBX9LnpttTG1vsjeqMXERVzdtolthe6NuN2DoXpTHSyyDpDkW6Z271mOqo6otYlzT1sBhd9aq7p+sSZva9+iLS47KmrytfBknjpy9MXaVy/SdxutSrZyPRba36YtUXsm5f1aBqhL9aFadf66E1upPUIDMB/MvT5dUrlc9Lw6uriHXnJz0PsYa68n4Afac3oqr0fUG3W+r+GLrpSK8yo4cF6kU8dC/cykBm9JznGlaN7sQliXywKE63p+p7YfUOT7r6Vk+nqu9Zukq58j5dMtWTROghPbr5TH/2i7PK12XV96fKsXmjz/vjxfY2dVZuorphV/nMStWx6E26DUK3i+p1BDVMusdc9RhdNaLbUXX1il4JQg9z0css6fFcSrdB6N53//J0ebwuYer/MN2DV489/ZW5XR9b9/bVg641wrpnnO41d+1HcXrF/F+Yx9RThOlz0RenbvzXx9bThX22PJYHTIh1W0Xl89J46ypifXxdJZ3XOULAR70V1YzGUzdV6dLj35oZbFtMK2Uz/7804/V79L3kYAs4umChj5mtRq6k21GzsOsqYF0y7sv39I66+P1Qlm21t6mzchPVPWaxe8768vGqfRUEfeFpDPXk9QfbS01fIHpOXl061bBpZK+eGKXnttSlyRs+idLYZtsO9HfRs53okqxeh1Vv1/t17k331tNLMumL9GAnmdafp+HWK+qf926UPv6RL9rHAsin3o4qOkZXW+vMwYcLQtnVbG9TZ+UmqmrbnlAuHV86YJUDANQyoppPujBz/MvlI1BsTeqKXEVVNxJPW1U+/ITjLAHUC6KaP9oYXc39zk+hbG+0N6krchXV1jazCN4UyrBJ5QOTbX8IAKg1RDV/dI3okLdDWb8zlGbTHluTuiJXUc38tKF8Xbta2MANAO0hqvmih0rqCSumLOuZw2gq5TKqetzqG3PKe4+xFyuAWkdU80P3UNZDfPSEQ42mNa2WBnVHLqOqdKel56aX0mOobH8YAKgVRDU/9NDJGz8OZfNue3u6K7dRbWkLZeX2UO6YXGJpFUBNI6r5oEupF75bknkbS2ljbO3prtxGVem67qVbzQvyo/JGZdsfCQDyjqj2PV04O/31UKavCWV3Dx2TapPrqCoNqx5DdINZXE/PgctSK4AaQ1T7jsZUT9Kje/pqUHc22VvTU3If1cyKbaHc83l55yX2CgZQS4hq39CTO+jC2OXjQ1m4qdTje/ra1ExUle689Mqs8sVk9aoCun7c9ocEgDwhqr1PT/D/94+H8sCXoWx0tFOSTU1FVXd9bmgunyP4ig/KZ8PgzEsA8o6o9i69kMmZb4Ty2dLyCYX0xEK2prhQU1FVGlY9+f6aHaF8sjiUk14tXzXB9ocFgDwgqr1Dd2gd8Hwo434MZfnW3g+qqrmoZjSu+gfT67C+OjuUy82S678+w2XPAOQPUXUjvcrMiPLl6ga/rec2COWHNeVz+bo6ZKY9NRvVSrpKWI9pnbgwlNsnl3eb/sOYUH4xqrwUq6uJdecmYgugLxDV7tH3br00py40/dVD5ctv/va58prK6z8K5a25oSzeXF7QsjWiN9VFVKut2xnK9NXlP7TuMXzhu6Ec+7L5n/Bsee9hnasBgN5y/9CvZfzpL1vvw6Hpe7auhTzqxfLSqF5w5eVZoXyzIpRVZmGqudXegb5Sl1EFgDwpvfm1hHe/bL0P9YWoAoBjRNUfRBUAHCOq/iCqAOAYUfUHUQUAx4iqP4gqADhGVP1BVAHAMaLqD6IKAI4RVX8QVQBwjKj6g6gCgGNE1R9EFQAcI6r+IKoA4BhR9QdRBQDHiKo/iCoAOEZU/UFUAcAxouoPogoAjhFVfxBVAHCMqPqDqAKAY0TVH0QVABwjqv4gqgDgGFH1B1EFAMeIqj+IKgA4RlT9QVQBwDGi6g+iCgCOEVV/EFUAcIyo+oOoAoBjRNUfRBUAHCOq/iCqAOAYUfUHUQUAx4iqP4gqADhGVP1BVAHAMaLqD6IKAI4RVX8QVQBwjKj6g6gCgGNE1R9EFQAcI6r+IKoA4BhR9QdRBQDHiKo/iCoAOEZU/UFUAcAxouoPogoAjhFVfxBVAHCMqPqDqAKAY0TVH0QVABwjqv4gqgDgGFH1B1EFAMeIqj+IKgA4RlT9QVQBwDGi6g+iCgCOEVV/EFUAcIyo+oOoAoBjRNUfRBUAHCOq/iCqAOAYUfUHUQUAx4iqP4gqADhGVP1BVAHAMaLqD6IKAI4RVX8QVQBwjKj6g6gCgGNE1R9EFQAcI6r+IKoA4BhR9QdRBQDHiKo/iCoAOEZU/UFUAcAxouoPogoAjhFVfxBVAHCMqPqDqAKAY0TVH0QVABwjqv4gqgDgGFH1B1EFAMeIqj+IKgA4RlT9QVQBwDGi6g+iCgCOEVV/EFUAcIyo+oOoAoBjRNUfRBUAHCOq/iCqAOAYUfUHUQUAx4iqP4gqADhGVP1BVAHAMaLqD6IKAI4RVX8QVQBwjKj6g6gCgGNE1R9EFQAcI6r+IKoA4BhR9QdRBQDHiKo/iCoAOEZU/UFUAcAxouoPogoAjhFVfxBVAHCMqPqDqAKAY0TVH0QVABwjqv4gqgDgGFH1B1EFAMeIqj+IKtBalGDLdinMnS+lN96ScOSDEt10s0TXXifRzbdI+ODDUnrrXSnMXyTB1p3peOvjAAdBVP1BVOGvtpIEG7dI8fMvJXzoYYkvuliSk04WOfJIkT/8QeT3vy9/PuooSU4+ReJLL5Xw0cel+NVUCTZtsz8mYEFU/UFU4aemNglWrZPS6OclOeNMkf79RX73u/b1HyDxOedK6eVXJVi7QdpaCvbHByoQVX8QVfinOZBgzXqJ7rhT5Igj7PFsRzJwoIT3DZdgwxbCinYRVX8QVXgnWLpSotvv2LeK1xLNdun3DRggkYZ19XrrzwEyRNUfRBVe0SXL8Oln0yVNayw7w4Q1OfpoKb30CttYcUhE1R9EFf5oLUrxk0mSnHmWPZJdpNtYi19+w17BOCii6g+iCm/oYTPRnXd1fKekjuo/IN17ONi20/pzAaLqD6IKbxRmz5V4yHn2MHZTfPElUpi30PpzgY5GNVixWUpPfSjx4JGS/PYqkV9c6M6vL5d40J0S3j9OCtOXWJ8POo+owhulF1+W5IQTrFHsruTkk6X0xtvWnwu0G9XmgoQjXrfHr5dEQ0dJYRE73XUXUYU3omG3d/kQmnYdeZSEw0dafy5wqKgGyzdJfOrd1tD1un++VIqfzrQ+T3QMUYU3dBVtehiNLYrdZR43uu56688FDhbVYPMuSY67zR64PlScMveA54qOIarwRjx4cNePS22Pedxo6BXWnwscLKrR1U9bo9bXkv7XS7C98YDni/YRVXgjvvAikcMOs0exu3RJ9ZprrT8XsEW1OHn2gUFbtVn2fmxrELn4kfLtw14QaQ1+vsN8zFiy73uq7/vgu333dUM48s39ni86hqjCG3rFGTn8cHsUu+uIIyS69z7rzwVsUY0ue2z/kGkMsyiO+UikFO6Lp8ZWw6kB1dv0Ph2j0dX4ZgHWcdl9lY/dFb+6TNoa2/Z7zmgfUYU30pPnH3+8PYrdlJx4kpReHWf9uUB1VIMdjfaQZaqjWqkyqtlSqsY0uy8LcxbpyqXfbFz2fVmMK7+v4mcVJ83a7/dA+4gqvFGYPlPic8+1RrG74gsulMKPP1l/LlAd1cK0RfvFaz+VS6zV91UusVbeVrmkmt1fGVUdVx3O7P6NO8qRzsZVCB9/f7/fA+0jqvCGnvc3um2YSL9+1jB2Wb/+Eg4fIcFmzv8Lu+qoFid8f0DA9lO9BFqpOrrZKmD9qAxu9bjqx6z8voOsMo5uf2G/3wPtI6rwR0tBiu99IMmgQfY4dlFy2ulS/HQy5/7FQXU6qqpyqbPy9so4ZmGsXI2bBbK9qKpsjC3eBlHtPKIKrwRrNkj4kHnzGTDAGshOO/xwCZ96RoL1m60/D1CdWv2rqmNZeV/l9tbqba+VX7cX1ezr7CMbV4HVv51HVOGXtpIU5i+S6Nrr7ZHsjMMOk+iW2yRYtip9XOvPA4wO7ahUuZRZGcdDLY1mYay8LwtkFlXbffrzNK76OPq1PobSx6t4Tuyo1HlEFf7Z0yKFpStMWK/r+iE2Rx2VHqITrFwjbY2t9p8D/Kw6quqAQ2qyeGYflatks8hmH5VLldX3aTz19iyq81buuz+7L/ue7GdkY7P7FYfUdAlRhZ8aTVjnLZLwwYclGXRqx3de6tdfktNPl/DxJ6SwaKm0NfGmg/bZomo9+UNPykJZGeBO4OQPXUNU4a+2UrqNtfTu+xJdf4MkJ51cjqueH1jPvKSnNNR/H35EenxrfO5giW4dJsUPP5Jg3Sb7YwIWtqgqp6cp7EZUOU1h1xFVoKUgwYrVUnptnMSXXZ6eeF+vuxqffU56/G' +
    'l0861SGjNWCj/MkmDTtgP38mV7KtpxsKhyQv36Q1SBaiayHQ6lBrahufw9tvsB42BRVVz6rb4QVaArNLq7m6T43niJrr9Ril9NZYkVB3WoqKa4SHndIKpAV5gl1GDjVokvvUyS446T6O57JFi9zj4W3ms3qj8LVmyW0lMfSjx4pCS/vcoavx7z68slHnSnhPePk8L0Jdbng84jqvCenr4wWLdR2rbv7vjSpo7b0yKl0WMkOeEESU4+RUqvvJbexhIrqnU0qqh9RBV+M0ucpXFvmCXNe6U44WNpaw7s42xMPINVa9PrqCZHHSXxJZdKsGY9UcUBiKo/iCr8trMhjWJ6kfErryqfyKGTUSx+Mlniiy6W6P4R6SE6nAMY1YiqP4gq/GXiWZg7X+Lzzpfk2OMkfPrZri1l7txTXkLd0UBQYUVU/UFU4S8TwPSqNSefIsmZZ0nxm2/t49qjIVWs9sVBEFV/EFX4y0SwOOGjdPVveM996QkgrOO6QndY6sz2WdQ1ouoPogqPldIzJOlVawpzF0jbrh44LZtZYtU9iYuTv5DCjNnS1tBkHwevEFV/EFWgJ+lhNs+OluTEkyS67nopLFzCamEQVY8QVaAnNbZK6b3xkpx0ksiRR6YXROfScCCq/iCqQE/S1b/bdqUn4U8GHi3xWWdLccrXLK16jqj6g6jCPxq+zdulNPp5KX72hQRbttvHdZUJaGHWXImuuFLi885Ld4Yiqn4jqv4gqvBPQ7MUvvnOLEkOTC/zVvhpgX1cd+xqlOKnk6U48ZP0NIjWMfAGUfUHUYV39ET44RNPphchjy+8SAoLHJ1MXJdOWUKFQVT9QVThncKipRIPHSpy2GES3nO/BGs3Wsf1uCyyhNY7RNUfRBXeKUyfIcnpp6dRLX4wQQI9vaBlXE/TbbfByrXpaQ1t96N+EVV/EFV4J9iyQ4rfTpNwzFgJNmyWtpaCdVyPaQ4kWLpCwmF3SHTtdVL47geWVj1DVP1BVOEnDd3WHe6DqvRnLVwi8ZlnSXL00RLde1/5+q22sahLRNUfRBVwTZdKTVjDRx6T5NhjJRk0SErvvFc+NzBLrF4gqv4gqvBLdkUZ232OBUtXSnT1NZIceaREl14mbVvMknIfPRf0LqLqD6IKf7QUJFi9vu+OGzUB1WNXw+EjpfjlNyyleoSo+oOowhvB+k0S3j8iPeFD6YWXrGNc0z2Ng83beuaKOKgZRNUfRBXeKMyeK/F556dXkCm9Os46BnCBqPqDqMIbpTffkeSkkyU+d7AUfphlHdPrmtok2Lil146VRd8gqv4gqvBGdMedkhxzjETX3SDB2g3WMb2qpZBebzV85NHyNlYTWOs41Dyi6g+iCj+YgJWeG5PudRuOerLv97rVnZS275Z48GCRfv0kuulmKSxfZR+LmkdU/UFU4Y10JyFd1WpiZru/1zW3SentdyU5+eT0+FU9yT8XNK9PRNUfRBXoK2ZpVfdIjm66pXwZuiFDpDDzx945yxN6FVH1B1EF+pIJa2HqNImuvyHd5lv48SdOCFGHiKo/iCrqmwZqT3N6hZi23U35XArcuSfdYSnQbaqcEKIuEVV/EFXUNxPSwnfT0/PuFj+fkl6hxjoOcIio+oOooq7pKQnDhx6R5KiBEl1zrRQWL7eOA1wiqv4gqqhrhcXLJL700vSC5OGjj/XdeX87Slf/7m6U4tRpUpg+U9p2cUHzekBU/UFUUb9ai2mY9HAVjWrxsy/K21VtY/OiqU2KU75Kz0+cXtBcz/zEdtaaR1T9QVRRv5oDKXz5jcTnnCPxWWdJsHJN/vesbWw18Z8iyamnpYfZRHffI8Hm7faxqBlE1R9EFfXLBFR3TNJjP4ufTK6N8+vqUqkJazR8ZBrV5IwzpPjRp/axqBlE1R9EFfVNI6VLp3ooTQ2tRtULmsdXXCnJ0UenS6ucEKK2EVV/EFUgj/a0SPHLr6X49rsSrNvEdtUaR1T9QVSBvNILme9sIKh1gKj6g6iiLukZlHRbauHHeeUTPtRLmPT3ILI1h6j6g6iiLhWm/SDxRRdJfPGlUvz62/zv9dse3elq+67ydWB16dU2BrlFVP1BVFGXSqOfl+S44yU+91yzxDq7tqOqz33rTik985xEV14lxUmf28cht4iqP4gq6k9Tm0Q33ChJ//5phDRINb3KtKUgwZr1Ep9/viRHHSXRrbdJsGqtfSxyiaj6g6iivuhq0jUbJL74YkmOPkbChx6u/cNRdIbATHull16R5MSTjBMlfG5MOvPA9tXaQFT9QVRRX0xkgk3bzJvYOxI+9rgUvvnOPq4GBSvXSnTLrelpF+NLLi0falPr24o9QVT9QVRRnzQ2Dc1ltvtrVHHK1xJdd72UxrxQXq1NVGsCUfUHUQVqSUOTBBpTzrBUU4iqP4gqUEt0GyrbUWsOUfUHUUX9aG6TNr2ii57sQXfisY2pR3ta/Pp9axBR9QdRRd0Itu6Q0ugxEt53vxQ/rZGr0nRHS0EK8xdJaczY9HJxub9WrMeIqj+IKuqD7vW7YrXEQ4aI/OEPEj7zXP1fh9QsnYaPPJoeZhNddbUU5i1k1XBOEVV/EFXUB70g+cwf0xM+SL9+5VMT1vsqUfM7Fyd8XL6g+dFHmyX04eWT8BPW3CGq/iCqqAu6R2zp5VdFDjssvbB3YeES67j6YuK5p0WiO+8SOeIISU47XYofT2LP4Bwiqv4gqqgP23dL6aWXJb7wIgnvuU+CdRvt4+qNWSrVGYjommvT370w5WuOXc0houoPoor60NQmweZtUpg7XwoLFtfdSR8OaXdj+TJ3P8yUYNsuVv/mEFH1B1EF6oGGlCXU3CKq/iCqQD1qDsoIbS4QVX8QVdS+bCmN1Z5l5u+gFzNPV4Pr3sC2MehVRNUfRBU1r/DjT1J6+10pfDdd2nbu8TuuTW1SmD1H4osuThW//MY+Dr2KqPqDqKK2mYCWnhsjyelnSHT1NRKs3+z3Kk89y9LCJRKffXb5gua335EutVrHotcQVX8QVdS0YPtuiW68SZIBAyS+9PJ0T1ivl1T1d9/TIqVnR6cXM09OPllKr44rb1/1+e/Sx4iqP4gqappuN9TVnMnRx0j42CjrGB8Fy1dLdPMtkpx0kkTXXidteh5kotpniKo/iCpqWvHzLyU+99wU2w/3V/ziKwlHPSmF2XOt96P3EFV/EFXUth27pfjVN1Kc8JEEG7bYx/hKL4XX2CJtLYH9fvQaouoPoorapjsl6SXP9NARrimKnCKq/iCqgC/MzEewam163Vnr/XCGqPqDqKJ2cbagjtEdlMxSfHHSZxLecWd6AXfdQ9g6Fk4QVX8QVdQmPYH+itUSbNxqAtHMnq2Hon+bHQ0SX3BBeuiRXtEmWLbSPhZOEFV/EFXUJL20mx6DGZ99jhQ+/1LaGlut4/Azs1RffPd9SQadKsnAgRI+8BBL+r2IqPqDqKL27GmRwvczRP7wB0mOPVaK33zHkmoHBFt2SHjX3WlU47POKp/WUU8KYRmLnkVU/UFUUXP0uqnhM8+J/O53Ep93nhR+WmAdhypmxqMwY7ZEw26X8ImnJFiznqXVXkJU/UFUUXOClWvSswXJYYdJdOddJg6c27ajgh0NUli6QoK1G633ww2i6g+iipqjEQ2fHWOWUs+X4vgP0/P/2sYBeUFU/UFUUZt0G2pDMyeK7y7927UUyquB+Ts6Q1T9QVRRu4hA95i/X6CneRw/QYqTPi9f4cc2Dt1GVP1BVAFfNbVJ6bXXyxckuHyoFKbPtI9DtxFVfxBV1JRg2y4JNukJHzgjULc1B1KY+l16eE1y9NES3XGnBOs2sQbAAaLqD6KK2mEiUHr3fQmffFoK335vH4OO03iamZPwoUfS432TU0+V4gcTOczGAaLqD6KKmhFs3i7RrcNE+veX6KqrrWPQecGS5RLddIskgwalMyzpjkuWceg6ouoPooqaoSd5iC+8SJLjj5dw9FjrGHSBiWhh5hwpfjW1vEe1bQy6haj6g6iiZqTnrj35FEnOPpvVvz1Nz51MUJ0hqv4gqqgZpdfflPjiSyS6bZgEq9dZx6AH6TZXdlrqEUTVH0QVNUNPradLqOlqykb2/nVCI9ocSLBqnRTmzk+3Y1vHoVOIqj+IKoB9dM/fjVslvOue9NjV4sRPuJJNDyCq/iCqAPZpKUiwbJXEZ5wh8vvfS3ztdRKs5YIF3UVU/UFUAezz8+rf0tvvpIfYJMceJ+HjT5SXVtm+2mVE1R9EFfmmS06bt0nprXek8ONcCbbttI9Dj9IzK0V33CXJccdLfOll5R3DOClElxFVfxBV5NvuJil+8VV6tp/46mtMWH+yj0PPMgHVncLCBx+S4kefSNvOPUS1G4iqP4gqci3YtC1d/Sj9+kl8wYVSmLvAOg4O6HGreuUaYtptRNUfRBW5lu40c8WVIocdJuGIkRKs32Qdh97CdtWuIKr+IKrIr7aSFGbNkeSYY9I9UdPVkLu45mdfCnY3cYWgLiCq/iCqyLVgy/Y0pnollWDdRlZF9hU9P/D3M9PLwxXfG88pDTuJqPqDqCLfNKLmDTxYvzm9qLZ1DNwzf/v0EnEnnSTxZZelaxCs42BFVP1BVAG0z8zcFCd/IfGZZ6ar46O77pZg606OXe0gouoPoor80jds3rTzY3eThA88KMnAgZKcfkZ6qBOnMOwYouoPoop80gtl72hgp5icKSxcItFNN0t85VVS+GFW+f+TZRz2R1T9QVSRS8GaDRKOfDA9nCbd65c373zY05z+vwnWrC/vrMSahA4hqv4gqsilwvSZEg85L70oeend91nNmCeslu80ouoPoopcKr30iiQnnCDJ2WengWVJNcd0FX1jK4c7HQJR9QdRRf6YN+fo9jskOfJIiS+7XIKNW1kyyiP9f7K7UQrzFkph6jRp27bLPg5E1SNEFfmib9Q790jpsVESn32OhMNH2Meh7zW1SfHTzyQ+7XSJzzlXip9NsY8DUfUIUUX+6GrEHQ0SbNhSPumDbQz6XktBgiXLJR48RJIBAyTSC5qvXs9aBQui6g+iivzSN2feoPNL/9/saSlv/z7pZElOOFFKY8ZyQXMLouoPogqgW4JVa9MzLOnZlvRUhulOS5ZxPiOq/iCqyA9d7avHQe7YXd6jlL1Ja4NZKi1M+0FKL78qwYo1LKVaEFV/EFXkR0OzFL83b86vjpPCzB8l2LXHPg6oMUTVH0QVuRFs2ibhyAckOfY4ia67QYIlK6zjgFpDVP1BVJEbwep1Ep9/gcgf+kk46kkJNm6xjkMN2NkgwfJV6YyS9X7PEFV/EFXkQ3MghTnzJTnyKJEBA6T42Rfl7aq2scivtpIEuxql9MKLEl1zbfkUk3u4oDlR9QdRRT6YgBY//1KS009Pz/mrV0OxjkO+tRYl2LZTosuHls+INfQKKcxfZB/rEaLqD6KKfDBLqsHajekSanH8hxJsZrVhLdMrC+k1V5Ojj5bwnnvLh9l4vFcwUfUHUUV+6JuuHkajOCyjtu1qTE8xqavyk0GDpDhtenpaQ+tYDxBVfxBVAD3PzBTpifbD+4dLadwb0ra7iSVVouoFogrADbO0GqzdwKp8g6j6g6iizwVbdkhh9lwpLFgswc4GzqSEukNU/UFU0ecK306TaOgVEl19jRR+mFU+IbtlHGqcXtVm++50Cda3VcFE1R9EFX2u9NyYdC/R5LTTpfDTAqJaj0xEdTVw6YWXpDh+gnfHrhJVfxBV9Ck9v2906zCRfv0kvuCC8pste/7WHzOjFD76mCSnnJKeNav41VT7uDpFVP1BVNGnCstWSnzZ5eXjGR94kKDWq9aiFKbPkPjcwelJIaLrb5Bg/SZvtp8TVX8QVfSpYMNmKb3ymoQjH5TCd9OtY1AHdGZJT1/47Oj0YuZ67Grp/Q+8WdVPVP1BVNH39rRIsG2XtO1osN+PuhEsWyXRPfdKfNHFJjRvE1XUHaIKoPfoDktLlkth7nyvDp0iqv4gqgB6l8a0pWC/r04RVX8QVfQNPWZx68501S8ne0C9I6r+IKroE3rmpNKYsRI++nj58Ao9N6xlHOqY7rzU1JZeGk4v+xes32wfVweIqj+IKnqfbldbt7F8abD+A6Q09kUJduy2j0X9ai1KsHqdRNffKPGFF5VPCqGXiLONrXFE1R9EFb1Pl05m/ijyu99JcsQRUpz8uXfb2GDoJoClKyUeMsTMXPVPT1UZLF1hH1vjiKo/iCp6nZ5AX5dONarxOeemJ9O3jYMH2kpSeuud9LjV9AQgIx+wj6txRNUfRBW9Lti8XcKnnpHk1FMluv0OCVats46DH/ScwOHwkZIcd5xEl10ubRu21N3Oa0TVH0QVva+xNb3OZuH7Genl3thJyXMmoIU589K1F4UZs9PNA+lOTLaxNYqo+oOoAuh7Dc3lS8LV6eFVRNUfRBVAPunSap0ssRJVfxBV9C5dEtE9fet0iQQ9JDs5yG6z9Gq7v8YQVX8QVfSqwvzFUvz0s3QbWno2pTrbdoZu0tdDcyDFjz6ReOgVohc1T18ntrE1hKj6g6ii95ilj9JLr0h8xhkSXXW1tOmSCFFFtdaihHfdLcnxJ0h84YXlnZds42oIUfUHUUWvCbZsl+jOuyQ5/HCJLh9al3t5omcUv/xG4nPPTY9djW69TYKNtX2YDVH1B1FFr9FzvMaXXJIej1h65jnrGCC1c4+Ejz1uXivHS3LmmVL49vuavvYqUfUHUUWvKX4yKT2DUnzu4HRJxDYGyBQWLkkvaB7dfW/6b6KKWkBU0WuCNRuk+N4HUnrltfTftjHAXiaiwfbd6VJrre8tTlT9QVTRe3RJY2eDBDsayttTbWOASrrNvQ62uxNVfxBVALVDj1utwUOxiKo/iCqA/DMRDTZsSbfLFyd+nJ6E3zoup4iqP4gq3NOz45g3xPSNsA4O5EcfMK+h4oSPJD79DInPOluKH08qn5nLNjaHiKo/iCrc0iWMjVsk0TfDq66R4tRpdbGNDL2stZjuAawXNJff/z69RFywblPNvJaIqj+IKtza3SSFr6ZKcuRRkpxyihQ/n2IfB7SnqU1K494wr6NBkhx7rISjnqyZNR9E1R9EFU7pBclLTz0j0r+/xOedL4Uff7KOAzpCD8UKh49Iz7akp7yslb3Iiao/iCqcClavk+jGm0T69ZPwnnvTi5PbxgEd0lJIL8agJ9wP1rP6F/lDVOGURjS8b3h6JiXdczM9kN8yDqhnRNUfRBXutRZNXDdKW0MzOymh5+lrSs+4lOOzLhFVfxBV9A59wyOocEAvZl74cV55b2DL/XlAVP1BVAHUJl0DYkIa3n2PxBdcmJ5Tuq2x1T62jxFVfxBVuKFLpbsapW3brlyvlkMN06hu2SHRNddKMnCgxBdfIoVZc+1j+xhR9QdRhRt7WqT4xVdSevX1dG/NWjr7DWpLcfIXEp91liTHHJNeBD+PV7Uhqv4gqnAiWLcxfYOTI46Q6IYbyzspWcYB3aYXNH98VBrV5OyzyzNxOTt+laj6g6jCicKsOel2ruT446U09sXcbutCHWgrSeGnhVJ65rl0qTWPmxuIqj+IKpxITyd30kmSnHmmFKZNZ/Uv3NrTXL6guW7Ht93fx4iqP4gqnCg9O1ric86R+MqrJFi/mcNp4DWi6g+iCieC5avT617q5bpYSkWva2pLTziilxzMwwwdUfUHUQVQd4KlKyQcPlJKL78qbTsarGN6E1H1B1EFUF/Mkml0192SHHWUxIMHS/HLb+zjehFR9QdRBVB3Cj8tKO993n9A+YLmekWbPtwrmKj6g6ii57QUJNi0TYpTvpJgyXJp29n3q93gqYYmKb3wkiQnnZwqvvVunx7WRVT9QVTRc3Y3lc9uc8EFEt15txTmL7aPA3pBsGKNhA8/KtGtt0nx62/79IQQRNUfRBU9JtiyXcKHHknPohRfcqmJ6iLrOKBX6JoT3QN4+ao+3wOYqPqDqKLHBGs2SHzRxSL9+pm4PlzejmUZB/iGqPqDqKJn6BVDFiyRxCylJocdJsWPJ3FqQuBnRNUfRBU9o62UHmhfeukV8+ZxjwRLVnAWJeSHvhb3tEhh+kwpvTs+XS1sHecIUfUHUUXPaQ4k2LrTvGFtSPe+tI4B+kJrUQrzFqWnzYwHD5HS62/16o5LRNUfRBVA/dOoLl4u8eVDJTnyyPIFzRcs7rW1KUTVH0QVgDeKEz+R5PQzJDnm2PQ0hr21tEpU/UFU0X16pprmwH4fkCPB9l0SPvyIJAMHSnTlVdK2eXuvnGmJqPqDqKLbglVr00NoojvvkuLUaez1i/xqKUhhyXIpjp8gwer1vXYFJaLqD6KKbit8Oy3d+SM5ZZAUP5yY7mVpGwfkgs70NTT36t7pRNUfRBXdY96YSi++LMmxx0ky6FQpzJrTp6eDA7pEVwE7XA1MVP1BVNE9Zqk0vOdeSQYMSC+zFezcw/GpqB3mtRps2yXB0pXpxSBcvXaJqj+IKrol2LhVwvuHS3LKKRLed791DJBLGtCGZimNHiPxeedL6ennnK1lIar+IKroHj1p+Y4GCVavS3dYso4B8qo5kOiWWyU5+hiJh5wnBd3Rzjaum4iqP4gqeoZuj+qlPSmBHmOWVvXUhfH556cnhYiuuVYCPcymh1/LRNUfRBWA13RNS2nMWElOPlnis86WwozZPX7cNVH1B1FF1+j2qD3N6YXJOfEDal2wdIWEDzwk4TPPSbB+s1lSJaroGqKKrmlqS+foi5M+l2DlWsKK2qare3UGkR2V0E1EFV0SbN8t4YgHJDn+hHRHj2DFaus4oGY4OpxGEVV/EFV0nnnzCTZukfjMs0T69ZPw6Wcl2LrDPhaoVTsbzNJro/2+TiKq/iCq6LzGVinMniMyYEC6x6Re+YPVv6gbOtO4dKWURo9NzxamF9+3jusEouoPoorO290kxU8mS3LyKelB84WZP9rHAbWotSil9z6Q+IwzU8UJH3d7WytR9QdRReeZJdVg+WopvfV2eU5+/Sb7OKAW6bGri5ZKfPnlIgMOl/jCiyRYttLEtuvHrhJVfxBVdJ3u2OFw5w6gz5jXdemNt9O1MXq2pfChR8pXtrGN7QCi6g+iCgAWujNe+NjjEp9/gZQ+mNCtVcBE1R9EFQBsmgMJlq9KL2eY7t3ejUvDEVV/EFV0ip4XtfDTgnSbaltDU5feaIKlGyV8YrzE54yQ5LdXifziQrd+M1TiU++RcOTr5g1yufU5AVY9tInDi6g2F8zv+ZVEVz4hyeE3iPzyIvv02Bn/eLEkA2+W6IbRUpw43f5zc4aoolMK33wn0VVXmxf5jVKYv6hzh9LsajFvLK/YJ55eFF39tJkp2Gx/jsCh6Ou9sbXTh5DVe1RLr02R5LBrrdNbT0qOv02Kn8ywPoe8IKroON15Y+yLIkccIcmJJ0mwxCz1dfDNpbBgnSQnDLNOKH3iX6+Q4hdzrc8VsGotpnu664xlZ/d4r+eoRre9YJ/GHAofe9f6XPKAqKLjtu2S6L77Rfr3l/iCC8s7bnRg1ViwepskR9xonTj6WuG7hdbnDOyntZAeVhMNvUKSUwZJ+OyYTl0erl6jGt0y1jpd9Ybw8fetz6mvEVV0WGHhEokvu1ySY441c4qjOrw9Nbr0MetEkQfJMbdIWyNng0I7zMxjsGO3RNdeJ8lRA8snPZk+q8PbW+sxqqWXJ1unqd5U/Cx/J54hquiwYPU6KT03RqK775HC1GkdekMpfjDtwIlhxhLZ+1EKRcZ8tO8+/bfeph+tgciwn1ct6Wf9OvtYtXnf93RTOCqfc7zIGfN6L3w1VeIhQyQZOFCiW4dJsGVHh5ZY6y2qwY4mkX8duv+09MF3P0+c5mNbg8jFj+y7T6fX7KP6vm6IT73b+vz6ElFFx+k2pW27ytuTzGfrmCrx4JH7TwhZNDWs+rVObNlElt2nE2cW0Sye+' +
    'jmLbOW4ysfuouT311ifO3CA7bul9OxzEg86VaLLhkqwcEmH9iuot6iWXpy0/3RUOV1XT7tZbPVz9fTfA4qfz7E+x75CVOFMsH67dSLYj05cOpHpxKb/rlw6PZjKiTabSDfuKH/WjyzSSv+dPWY2cVsm6MI3862/A1AtWLRMSq+OS49f9XX1b3zeg/tPQ5XTsX5dORNcOa46qtk4nU6zj2xmWcdkX2fTvGUpN29/V6IKZ3QOsvLFf4BsQskmPp3AGprL9MMyAaWyiU0/ZxNpNrY6nJX3H2SiVKXRH1l/B+AAui+BLp16vKOS/Pry/achnd4qo1r9tcqmzSyaSqf57LbqmeDKr/Vz9eP9LD7tHutz7CtEFe3TufH0RA+dO6G4vpFUTwB7ZROMfuiEpbdVTmBZcLP7MtmEmU1gWTSziGaPq7J4Zo+rH5UTdIVw+Djr7wB0h20aqPW4BtsbD/id9psOs2nQFsHq6Vo/ZxHVr7PpO5tOs6/1o/q94GfJH66zPs++QlTRvj0tUnrhpfRi5IXvZ6RfW8dVOWRUs9BVTlCVE1jlXGp2fzbh6kf1kuihopqNqbytClFFZxzytd1D8hpfa1RVZQDNe8R+026lyum8vageKtA/I6qoLbpz0satEp92uiRHH52e/KFtT8eu1nHQ1b8aQP2onlD09soJrHKCU/pv/dDbs+9pL6rZ19lHNq4Kq3/RGXtX5+oewVOnpXsCh088JYUFi6U4+Qvz7yclum3YPsNuL9t72+0SPvm0mUa+lGDNhgNmVPc+fsVteXLA6t9q1dNypnr6bC+q2XuFfmTfU/l4Bqt/UVvMxF6Y9oPIkUemUS1O/Ng+zsK6o1IWQf3IJpzq+3RCyiKaBVQ/60f1hJV9TzZhZhNlFs9sopw8s/y91SH/GTsqoTP2Rs/MdIYjH0yP3dazjEVXXiXxOedKeOfdaVyDxculbetOaTPvnenpDbfuSHd0Kn76mUS331ke++BDJsZL9ru0XN6jesCOSpXTbhbOymkwm+4qx+l92XRd+X3ZtJyN1TF6fzau8ucaefs7EVUckl6dozT6eZHDD5d48BApzJhtHXcwBxxSk00clR+VocuiqB9ZQLPAVn/oxJZNeEvW7RuThTj7vuxxKifSiufEITXorMroFeYvLJ9p6aijJLrueinMntuxy8SZyBZm/lg+l/Y110rxm+/23pf3qB5wSI3KAqkfldNYFsvso/I+/bdOozr96kfle4Hel31dHdzs+w0OqUFNCTZvk/DxUWZO/BiJ7rwrPQGEbdzBWE/+0JOyUFrmYDuKkz+gsyqjp6twNarhw49KsHZjeYm0I4fa6BgzNlizXsJHHpPoxpvTtUJ6X96jaj35Q1dkUa0KZUdx8gfUHp3oV6yW4tdTpTBnnrTtarSPOwSnpynsZlQ5TSG6Io3enS+mp+7UpdPSM6MlWLmmfLiNZfwhtRTSSymWnny6fPWnxcuk9PqUXEdV9chpCrsZVU5TiNqlc9X6htGROfAqnFAf9Sa9buhtz0v40CMSDbujfBnEThy3egDzvYW58yW69TYJH3/CBGuShHflO6qKE+ofiKiiV3DpN9ST0rgpEl07SpKTT5HC1992aQ3OAXbtkeKUryU59TSz1PpOuiRsHZczXPptf0QVB6dLpjr33ZVVWjZcpBx1ovTCxxKfPSy9ak2wYYt1TFfoNlndaSm6/kETqzHWMXnERcr3Iao4KN2Wml6Q2XzusbAawdKNEj4xXuJzRkjy26usE0+P+s1QiU+9R8KRr0th1nLrcwI6I3zqXUmOvcIssb4hbTsarGO6Qi9YUXr5NRNsE9Ybn7aOya3mQnm1+JVPSHL4DSK/vMg+PXbGP14sycCbJbphtBQnTrf/3JwhqrBrbJHSG29JfMaZ6bF3gR5r14XtqUA9Ch8ZZ8JxUfnwGd3b1zKmS/S48B9mmSWyi9LVy9YxyLVOR3XBD+vk60tfsT4Y6kewfrNE99wrMmBAerhA204zN05UgXTP3/iU2yU5bIgE6zZ2bwelaron8Mq1khxxtsSn3p77PYBxIKIKq8Kc+RJffIkkxx4npedGd/h8v0C9S6N68jBJfndu+UITPTmzqZtZtu+SpP8ZEg8iqrWo01Fd+ukC+7pvAPBAPGRkOaq/H1zentrDUdUdn5L+Z5ql1eutPx/5xpIqrAo/LZDS82MlfGxUuiq4J3dUAmpZuqRqliKTfudLsHRF+dqqlnFd0tQmwcIlkgwcIvGpd7CkWoOIKuz0TErbdpV3UGrhjENAJo3qaXeZ8F2Wnhi/bXeTdVyX7NwjxYmfmKAOlfj0u4hqDep0VNn7F4DvSqMnmKXV69Mr1ARbtlvHdIVeZjEcPkLiS++U6ObnrGOQb0QVADqp9MpkE76R6aXb0su2deSqNO0x76+62UWvBhXeP1bC28faxyHXiCr2pztKbNpanvtmj1/AKj3JwS3PmbBeJuGzoyXYsLl7OyyZ79XDc/TC5fEVV4qesakWzv2LAxFV7KM7I23ZIfGVV0l43/1S+GGmfRzgufQqNXe8KMXPpkg85DwpfvRp904C0dAsxffGS3ze+VL88hspjfuC7ak1iqhin4YmKX7xpSQnnCjxmWdK8dPJ9nGA59Ko6pLknhYpjRlbvsi47rTUlbCaxyhO/Dh9jNILL5Uf0ywJE9XaRFSxl+7pG456UpIjj5L4wovK10+1jAN8l0b15+jpIWelsS9KdP2N6bmA01XBHTnLUnNQ/t6XXi1fk9V8zk7OX/n4qC1EFXulpya8fKhI//7lvRrXbbKOA3xXHb1gzYY0qNH1N6TXWC1O+jw9hnXvvgkaWdXQLMHm7RIsWZ6uCQoffCj9ntKbb5dPeXiQx0ftIKrYS3dQ0jnm+Oxzev74O6CO2KKnx3UXvp8h0U03pxehCO+8Kw1t8YuvpDDzRynM+FGKn38ppddel/COO9Mx0c23pCfQD7bv3u+xiGrtIqrYR/debGhKd+sPtu20jwGQRs92irqeRFRrE1HF/jSsupqqJ89nCvhEpx09daHucPTKZwfGUo8/1VXCOobprO4QVQBwjNW5/iCqKM8t6xlhGprt9wPoFqLqD6IKadvdKIXpM9MD2INFS3vmlGsA9iKq/iCqkGDVWoluv0OSo46S8P7hB+yJCKB7iKo/iCqk8N10iQcPluTYY6X04ivStqvROg5A1xBVfxBVpMfSJccdJ8nJp6Srgbt1DlMAByCq/iCqvmstSumZ5yQ5ZVB6YvBg+67yifVtYwF0CVH1B1H1nQmonuwhPfPL2+/axwDoFqLqD6IKAI4RVX8QVQBwjKj6g6gCgGNE1R9E1VctBQk2bpHCvIUSrF7P2ZQAh4iqP4iqr/a0SHHSZxLrJaoeflSCJSvs4wB0G1H1B1H1VLCjwcT0EUkGDpToiivLpye0jAPQfUTVH0TVR20lCTZtk3jwEJH+/SV8bJQEm7fZxwLoNqLqD6Lqo+a2dFuqDBggiYlq8cOJ5Wuo2sYC6Dai6g+i6iPdSWnVWgkffFiim26Wwpx59nEAegRR9QdR9ZFeP7WxVYL1myRYvkqCnQ32cQB6BFH1B1EFAMeIqj+IKgA4RlT9QVQBwDGi6g+i6plg5RoJH3pYwsefkMK8RelJIGzjAPQcouoPouqZ4tdTJT53sCSnnibFSZ9zekKgFxBVfxBVn7QUpPTquPQsSskJJ0ph/kJpa2qzjwXQY4iqP4iqT3bukXDkgyL9+kk85Dxp291UPrzGNhZAjyGq/iCqHgnWrJfw9jskOfGk9CT6nEUJ6B1E1R9E1Sca0a07JdDLvS1ZzlIq0EuIqj+Iqm80pM2BtJn/l9b7AfQ4ouoPogoAjhFVfxBVH/x8rt90T9/Won0MAGeIqj+Iqg9aClKYv0gKM38sXzeVHZSAXkVU/UFUfdDQLOE990py/PES3XV3uhewdRwAJ4iqP4hqvdNVv9t2SXzmmZL06yelUU9K26499rEAnCCq/iCq9W5PS7raNzn66FTxvfFsVwV6GVH1B1Gtd7sapfj+B5KccorE550vhe9n2McBcIao+oOo1ruGZin8tEBKTz8r4VPPSLBmg30cAGeIqj+IKgA4RlT9QVQBwDGi6g+iCgCOEVV/ENU6FmzbKYVFSyVYu7F8RiVOoA/0CaLqD6Jar0xAC9N+kOja6yQcMVKCVes4kxLQR4iqP4hqvWoOpPTa6+kJH5KBA6WwYhVRBfoIUfUHUa1TwYYtEg4fITJggMSXXibBjgbrOADuEVV/ENU6VZi3KI1pcsyxUnrqmfR4Vds4AO4RVX8Q1ToVLF4m4WOjJLrhRil8NbV82TfLOADuEVV/ENV6tadFgnUbJVi2UoLN2znfL9CHiKo/iCoAOEZU/UFUAcAxouoPolqP9CQPnOgByA2i6g+iWm9ai1J66RUpvfyqFObM49hUIAeIqj+Iaj0xAQ02bZXk9NMlOekkKY19iagCOUBU/UFU68meFilOnSbJ8ccbJ0jxvfH2cQB6FVH1B1GtI8H23VJ6bkx6WsL4/AukMGuOdRyA3kVU/UFU60iwZYeE99wryZFHlk+iv3aDdRyA3kVU/UFU60lja3qpt+Kkz6Tw40/S1tBkHwegVxFVfxDVemT+P+lVajisBsgHouoPogoAjhFVfxDVeqHn9mXpFMglouoPolongo1bynv76nVTOXk+kCtE1R9EtR7sbpLi+A8lOftsia6+VoKtO+3jAPQJouoPoloHgtXrJbrrHpHDD5foGhPVLdut4wD0DaLqD6JaBwozZkt83nmSHHOMlJ4fK8HOBus4AH2DqPqDqNYBXfUb6/l+Bw2SwtTv0tMV2sYB6BtE1R9EtQ4Ufpgl4QMPSnTTLdK2fTc7KgE5Q1T9QVTrgVky1VMUBpu3E1Qgh4iqP4gqADhGVP1BVAHAMaLqD6Jaq/TMSc1BebWvHpfKzklAbhFVfxDVWtVSkGD1OonuvV/Cp5+Vwpz59nEA+hxR9QdRrVVmybQ46XNJTj1N4nMHp/+2jgPQ54iqP4hqrdq5R8LHRkly9NESXzZUCvMW2scB6HNE1R9EtRa1ldJTEcYXXSzSv7+EDz4swcat9rEA+hxR9QdRrUUa1Q1bJBp6hcRnnSWlDz+StqY2+1gAfY6o+oOo1qrWogTrNknh+5nm80b7GAC5QFT9QVRrmR5W01LgLEpAzhFVfxBVAHCMqPqDqNYaXTrVJVOWToGaQVT9QVRrza49Upg9V4pffi3BspXS1thqHwcgN4iqP4hqjQlWrJHo1tvS41PDUU+UT1FoGQcgP4iqP4hqjSl+N12Sc86V5KiBUnrtdQl27LaOA5AfRNUfRLWWtJWk9MZbJqhHSXLscVKYO5/Vv0ANIKr+IKq1ZE+LhM88a4J6rMRmaTXYbpZS29hhCcg7ouoPolpLzFJp4YdZUhozVkrj3igfo2obByBXiKo/iGot0sNpWO0L1Ayi6g+iCgCOEVV/EFUAcIyo+oOo1gI9i9KWHRKsWmc+b2dbKlBjiKo/iGotaA6kOPnz9KQPpWdHS7B2g30cgFwiqv4gqrWgsVXC4SMlGThQ4muulWDJcvs4ALlEVP1BVPNOV/3u3CPx2WeL9Osn4cOPSpsen2obCyCXiKo/iGreNbVJ4aeFkhxzjMiRR5qJ851yaG1jAeQSUfUHUc27Zo3qAomG3S7R9TdKYcZs+zgAuUVU/UFU805P9NDQJMHKtVJYuFSC7bvs4wDkFlH1B1EFAMeIqj+IKgA4RlT9QVTzTndKYsckoKYRVX8Q1RwLVq2V0tPPSunV1yVYtpKT6AM1iqj6g6j2pZaCBGs3SmHaDyac4yR88GGJbr/TuEPCESMluvteiU87XZJBp0px0ufStrvJ/jgAco2o+oOo9gWzxKlLocUPJ0r46GMSDbtDonvvk/CBB9OTO4SPPGb+/VB6GE085DxJTjjRjHs8PV61bVej/TEB5BZR9QdR7W0mioUFiyUc+aDEF14s4T33SeHLbyRYvrp8pqSmtrKdeyRYvS69KHn4+BMSX3SxRLcNk8K330vAGZWAmkJU/UFUe1NzkEYxuu56ia65Tgozf5S2hmb72EqtRQkWL0vP/xtfPlRK731QDq9tLIDcIar+IKq9KA3qjTen206DDVvSsyV1eM9evdzbtp1Seu11iYZeKaX3TVi5BBxQE4iqP4hqb0iXNJdLdMut6bbR9Lqoeqak6nHt0cfZuEWKb70r8cWXpKuGO7SkC6BPEVV/EFXXdEl0T4uETz2T7tVbmD23e0uYGtaVa9NtsrqncLB+E8exAjlHVP1BVF1rbkuPMY0HD5biR5+mOyBZx3WGiXThx58kOf0MKXw3naVVIOeIqj+IqmPBjt1Sev1Nia6/QYKlK6xjukIfN7zr7vLq5HUbrWMA5ANR9QdRdSzYsFmiW2+T0tgXJdi83TqmS8zSqi756p7E6Spl2xgAuUBU/UFUHdOdknTVb2HqtJ49I1JzIMGipRJfcqkUv/jKPgZALhBVfxBVx/SkDslxx0uwcEkaQtuYLtEdlrbsSM+4VJz4sX0MgFwgqv4gqo7pTkrJkUeW99LtymE0B6N7/Da2SnzuuVIc/6F9DIBcIKr+IKqOBctXSXL0MRKsWGOi2oMna9Cobt8t8eAh6TmErWMA5AJR9QdRdUyPKU3OOLN8ooY9LdYxXaJXuFm5Jj0ncHHyF/YxAHKBqPqDqDoWrNuU7qFbeuMtCbbutI7pksZWKU75WqKrrykH2zYGQC4QVX8QVccCPV/vmLHp2ZR0ydI2pkt27kkvGxfePzy9jJx1DIBcIKr+IKquNbakx5HG518gxa+m9szZj5raJFiyvLw99ZPJJrAN9nEAcoGo+oOouqY7FO1ukujOuyUc8YAEy1Z1by9gPZRmw5Z06TceemV6zdUe3asYQI8jqv4gqr3BRK8wa45EV16VnlmpbYdZsuzKSfD1e3Y1SvHTz8pLqZM+T7+2jgWQG0TVH0S1tzQHUhw/QaJrrpXSy6+WVwN3Nqx6asJPJkl0xZVSem5M1x4DQK8jqv4gqr0o2LZLihM+SvfYDR95rLzjUmOrdex+dJXv+s1SemVc+r0a1GDTNoIK1Aii6g+i2sv0pPq62ja6bVh6PdTSuDelMGdeGs10Va5ea1WZpVANZ7B4mRQ/mCDhfcMluvFmKb31jgRruSoNUEuIqj+Ial/Y3SSFeQslfPhRiW66WaJht5ulz9FSfG+8Ce5nUvx8SnrqwdILL6WXd4tuuFGie+6VwrQfevZYVwC9gqj6g6j2FV112xxIYdFSKb7/gUT33Z9ecSY+7XTjNIkvuCA9trX06rj0guTpFW5Y3QvUJKLqD6La1zSUSg+LSRV+ln1tEFOgphFVfxBVAHCMqPqDqAKAY0TVH0QVABwjqv4gqgDgGFH1B1EFAMeIqj+IKgA4RlT9QVQBwDGi6g+iCgCOEVV/EFUAcIyo+oOoAoBjRNUfRBUAHCOq/iCqAOAYUfUHUQUAx4iqP4gqADhGVP1BVAHAMaLqD6IKAI4RVX8QVQBwjKj6g6gCgGNE1R9EFQAcI6r+IKoA4BhR9QdRBQDHiKo/iCoAOEZU/UFUAcAxouoPogoAjhFVfxBVAHCMqPqDqAKAY0TVH0QVABwjqv4gqgDgGFH1B1EFAMeIqj+IKgA4RlT9QVQBwDGi6g+iCgCOEVV/EFUAcIyo+oOoAoBjRNUfRBUAHCOq/iCqAOAYUfUHUQUAx4iqP4gqADhGVP1BVAHAMaLqD6IKAI4RVX8QVQBwjKj6g6gCgGNE1R9EFQAcI6r+IKoA4BhR9QdRBQDHiKo/iCoAOEZU/UFUAcAxouoPogoAjhFVfxBVAHCMqPqDqAKAY0TVH0QVABwjqv4gqgDgGFH1B1EFAMeIqj+IKgA4RlT9QVQBwDGi6g+iCgCOEVV/EFUAcIyo+oOoAoBjRNUfRBUAHCOq/iCqAOAYUfUHUQUAx4iqP4gqADhGVP1BVAHAMaLqD6IKAI4RVX8QVQBwjKj6g6gCgGNE1R9EFQAcI6r+IKoA4BhR9QdRBQDHiKo/iCoAOEZU/UFUAcAxouoPogoAjhFVfxBVAHCMqPqDqAKAY0TVH0QVABwjqv4gqgDgGFH1B1EFAMeIqj+IKgA4RlT9QVQBwDGi6g+iCgCOEVV/EFUAcIyo+oOoAoBjRNUfRBUAHCOq/iCqAOAYUfUHUQUAx4iqP4gqADhGVP1BVAHAMaLqD6IKAI4RVX8QVQBwjKj6g6gCgGNE1R9EFQAcI6r+IKoA4BhR9QdRBQDHiKo/iCoAOEZU/UFUAcAxouoPogoAjhFVfxBVAHCMqPqDqAKAY0TVH0QVABwjqv4gqgDgGFH1B1EFAMeIqj+IKgA4RlT9QVQBwDGi6g+iCgCOEVV/EFUAcIyo+oOoAoBjRNUfRBUAHCOq/iCqAOAYUfUHUQUAx4iqP4gqADhGVP1BVAHAMaLqD6IKAI4RVX8QVQBwjKj6g6gCgGNE1R9EFQAcI6r+IKoA4BhR9QdRBQDHiKo/iCoAOEZU/UFUAcAxouoPogoAjhFVfxBVAHCMqPqDqAKAY0TVH0QVABwjqv4gqgDgGFH1B1EFAMeIqj+IKgA4RlT9QVQBwDGi6g+iCgCOEVV/EFUAcIyo+oOoAoBjRNUfRBUAHCOq/iCqAOAYUfUHUQUAx4iqP4gqADhGVP1BVAHAMaLqD6IKAI4RVX8QVQBwjKj6g6gCgGNE1R9EFQAcI6r+IKoA4BhR9QdRBQDHiKo/iCoAOEZU/UFUAcAxouoPogoAjhFVfxBVAHCso1ENVmyW0lMfSjx4pCS/vUrkFxe68+vLJR50p4T3j5PC9CXW54POI6oA4Fi7UW0uSDjidXv8ekk0dJQUFq23Pz90GFEFAMcOFdVg+SaJT73bGrpe98+XSvHTmdbniY4hqgDg2MGiGmzeJclxt9kD14eKU+Ye8FzRMUQVABw7WFSjq5+2Rq2vJf2vl2B74wHPF+0jqgDgmC2qxcmzrUFLrdosUgpFxnxU/nrYCyKtgez38cF3+3+PjtXv0e+tvL2LwpFv7vd80TFEFQAcs0U1uuwxa8z2xrEyqtlt1SGtpDHVjx6KqvzqMmlrbNvvOaN9RBUAHKuOarCj0R6yix8R2dZQjmNlVDWmlV9X0/uzjyyq2W1ZbPUjuy9b8tWfpT9zxpLy/VXRLk6atd/vgfYRVQBwrDqqhWmL9ovXXho3jd2SdftHNIte9lG5NJoFUr9HP9uiWvkYWTiz+zfuKP+sysf8Wfj4+/v9HmgfUQUAx6qjWpzw/QEB2xtHjZ/KopotvWZLlVkMdYx+n37W7xs90R7VLKLZ42f3H2ypuEJ0+wv7/R5oH1EFAMc6FFWNXeXq2IOt7q2Mo96v4zSc1dFsL6qVYypvq0BUO4+oAoBj7a7+zYJX/WELa2UcNb62D72vvahW/8xsXAVW/3YeUQUAxzq8o1KmI6t/qyNYHc1sXOXSr35k36fjsqVc/T6lj1HxmOyo1HlEFQAcq46qOughNap69W+2mjf70Purv+dgUZ23ct/3Zt+XPV712MrH5ZCaLiGqAOCYLaqHPPlDT8hCmS2ZdhInf+gaogoAjtmiqpyeprAbUeU0hV1HVAHAsYNFlRPq1x+iCgCOHSyqiku/1ReiCgCOHSqqKS5SXjeIKgA41m5Ufxas2Cylpz6UePBISX57lTV+PebXl0s86E4J7x8nhelLrM8HnUdUAcCxjkYVtY+oAoBjRNUfRBUAHCOq/iCqAOAYUfUHUQUAx4iqP4gqADhGVP1BVAHAMaLqD6IKAI4RVX8QVQBwjKj6g6gCgGNE1R9EFQAcI6r+IKoA4BhR9QdRBQDHiKo/iCoAOEZU/UFUAcAxouoPogoAjhFVfxBVAHCMqPqDqAKAY0TVH0QVABwjqv4gqgDgGFH1B1EFAMeIqj+IKgA4RlT9QVQBwDGi6g+' +
    'iCgCOEVV/EFUAcIyo+oOoAoBjRNUfRBUAHCOq/iCqAOAYUfUHUQUAx4iqP4gqADhGVP1BVAHAMaLqD6IKAI4RVX8QVQBwjKj6g6gCgGNE1R9EFQAcI6r+IKoA4BhR9QdRBQDHiKo/iCoAOEZU/UFUAcAxouoPogoAjhFVfxBVAHCMqPqDqAKAY0TVH0QVABwjqv4gqgDgGFH1B1EFAMeIqj+IKgA4RlT9QVQBwDGi6g+iCgCOEVV/EFUAcIyo+oOoAoBjRNUfRBUAHCOq/iCqAOAYUfUHUQUAx4iqP4gqADhGVP1BVAHAMaLqD6IKAI4RVX8QVQBwjKj6g6gCgGNE1R9EFQAcI6r+IKoA4BhR9QdRBQDHiKo/iCoAOEZU/UFUAcAxouoPogoAjhFVfxBVAHCMqPqDqAKAY0TVH0QVABwjqv4gqgDgGFH1B1EFAMeIqj+IKgA4RlT9QVQBwDGi6g+iCgCOEVV/EFUAcIyo+oOoAoBjRNUfRBUAHCOq/iCqAOAYUfUHUQUAx4iqP4gqADhGVP1BVAHAMaLqD6IKAI4RVX8QVQBwjKj6g6gCgGNE1R9EFQAcI6r+IKoA4BhR9QdRBQDHiKo/iCoAOEZU/UFUAcAxouoPogoAjhFVfxBVAHCMqPqDqAKAY0TVH0QVABwjqv4gqgDgGFH1B1EFAMeIqj+IKgA4RlT9QVQBwDGi6g+iCgCOEVV/EFUAcIyo+oOoAoBjRNUfRBUAHCOq/iCqAOAYUfUHUQUAx4iqP4gqADhGVP1BVAHAMaLqD6IKAI4RVX8QVQBwjKj6g6gCgGNE1R9EFQAcI6r+IKoA4BhR9QdRBQDHiKo/iCoAOEZU/UFUAcAxouoPogoAjhFVfxBVAHCMqPqDqAKAY0TVH0QVABwjqv4gqgDgGFH1B1EFAMeIqj+IKgA4RlT9QVQBwDGi6g+iCgCOEVV/EFUAcIyo+oOoAoBjRNUfRBUAHCOq/iCqAOAYUfUHUQUAx4iqP4gqADhGVP1BVAHAMaLqD6IKAI4RVX8QVQBwjKj6g6gCgGNE1R9EFQAcI6r+IKoA4BhR9QdRBQDHiKo/iCoAOEZU/UFUAcAxouoPogoAjhFVfxBVAHCMqPqDqAKAY0TVH0QVABwjqv4gqgDgGFH1B1EFAMeIqj+IKgA4RlT9QVQBwDGi6g+iCgCOEVV/EFUAcIyo+oOoAoBjRNUfRBUAHCOq/iCqAOAYUfUHUQUAx4iqP4gqADhGVP1BVAHAMaLqD6IKAI4RVX8QVQBwjKj6g6gCgGNE1R9EFQAcI6r+IKoA4BhR9QdRBQDHiKo/iCoAOEZU/UFUAcAxouoPogoAjhFVfxBVAHCMqPqDqAKAY0TVH0QVABwjqv4gqgDgGFH1B1EFAMeIqj+IKgA4RlT9QVQBwDGi6g+iCgCOEVV/EFUAcIyo+oOoAoBjRNUfRBUAHCOq/iCqAOAYUfUHUQUAx4iqP4gqADhGVP1BVAHAMaLqD6IKAI4RVX8QVQBwjKj6g6gCgGNE1R9EFQAcI6r+IKoA4BhR9QdRBQDHiKo/chnVhuZQlmwJZfz8UB7/NpQRXwL+GvlVKE9PC2XS4lDW7AilscU+3RxMS1soO5tCmbU2lFdnh/LwN/afA3cm3f+1zL3sZet96F2PmNf/m3NC+WlDKLtNa1rN9GGbbroqV1FtNfQN49uVoVzwbij/8EQo/214KP/xHsBf/+neUP77iFB+/XQowyaV3wyaWu3TUDUN6uaGUF43byJHvhDK3zwSyn+53/5z4M61530tr5z4svU+9K7/al7/f/dYKMe/HMqHC0LZ0VieTmzTT1fkKqrN5o1iwaZQfj86lP98n/0PAvhMg3jJ+6Gs22mfhqrpG8Z780L5s5HlONseE+4R1fzR6eFvHg3ly+XlJVbb9NMVuYqqvgHc9Vko/+sh+x8BQCj/MKq8+so2DVXTpVqdI/8jy+Og9xDVfNKZ1CFvh7Jim3366YpcRVVXU/UbU148t/0BAITyP8xS50Xv2aehap8sDuX/mrlx2+Og9xDVfNKlVZ1Jnb3OPv10Ra6iumFXKH9pllJZTQUc3B/fF0r/5+3TULW35obyJ8yk9jmimk+6BkeXVr9bZZ9+uiJXUV1vovqnI+y/PIB9/v1Z+zRU7fUf7d+P3kVU823qSvv00xVEFahBRLW2ENV8I6qA54hqbSGq+UZUAc8R1dpCVPONqAKeI6q1hajmG1EFPEdUawtRzTeiCniOqNYWoppvRBXwHFGtLUQ134gq4DmiWluIar4RVcBzRLW2ENV8I6pAvbm71Cn//kxJWtvaN262/fu7zPbc0S6imm9EFahltlh1Up9F1cb2O2I/RDXfiCpQa2wx6oZcRbWS7XcHUc05ogrUAlt0ekhuo1rJ9jfxFFHNN6KKLvu7x0IZ+mEkA1+KDrjE3n++L5T/93go90yJ5DfPhvJHlkvw6WWS/vyBUP7ywX3+u/l/pipvq/YX5nv0kmXVj1eXbIHptOIh/dszRWlpbd+4Wfbv7zjbc+sk29+oHf/TvF7+4YlQ/vqRA+/7W/Ma/tXTofxJF15Pehm8//VQKP/8VChHm2ng6omRXPBeJP/H8nPUuW9HMmZGnL6Gs+nhT4cf+Pr+85HlaaP6+9Uvn4zk85HfyLiT+yaq/9U83//98IHTs97+L09H6XP/pydDuXh8lP5dKsdU+8OYUO76IpJ/NOP1/eO/mcf4n1V/i0r6vlALl/Ikquiy3zwTybi5sZxv3kj+uOrFrhPAWW9F8u2aRI54IdrvvsyxL0cy2rzJvDArTj/rYw37LErffPRr9eZP5dt1jL4hjTWfX5wdp2+GtsesK7aotMsWs0Prvaja2H6Hdtj+Vofw2+dCGTMzTl+P1fdd+1Esr5vXmMZRr4dZeZ++pnUG7vhXIjnzzUguej+SGz6J5b4vY3l8WiwvmdfhG+Z735kfyweLYnlvQfn1+/+ZmcnKx8kM+yyWHzcm6YXeszhc9kGUft/r5jWu3poXyzPTY/nD8/Zp5nAzLe145Rt5/ZRyVPV5n/9uJA99E1sN/yqWPzOhy75fn9udX8TyYMWYS0wANWaHjY7kbnNfdvvIr+P099XY6ffq3+c3z0bp9KfPW0Ont+kMtM60fLEiSd8T9Dm+Zn6Xo160/w6ZQa9H6e/7hzFR+n5xnvk9Xp1T/nvq7dnfRL1r/kaPfhvLv5qfb3usPCGq6LLfmYnwvQVJOlHqkqNOYDr3rhPh35o3Dp1wP1uepG8QepvOzer92ZvX5WYp94f1STqx3DIplolLym9Sg9+J0q/vMK+NhVsT+XJlIvdOieV286b07A+xrNyZyK/NXHH186kbtpAclC1UnXBXQf7t6YI0t7TvtVmFdPwh2X5Gp9h+x4Ow/e0sTnw1Sl+Hulal8nZdOn38u1imr0vSeFZHVWPxL2YpViOikdCZu+wNf7aJ4/IdSRqBmz+NZYh5zR5mlrw0WlmEqt1lgrXAvJ512sii+pQJ6OpdiYwykVZvm8f/bm1inQFQukTc8sZUeePnqP7SxOzlH2OZY56PPrfM+wtjmbo6ke3Nify1WbLMvr+/mRaXbE/kk6VJGvM5m5J07N+PCtPpeK75evKy8vfrdDdrQ5IGV79X/z467gnzPH8wfzP9nTXqf2lofJsKItd8VA7zDDNd32tmPs42v4c68bUonZnInoc6/Y3y+0f/seWonmYi+4r5XdbsTuTTpbE8+X2c/iz9/fRvNHFxIr+qgemeqKJTdMLSCUCXFAeNi9K5Uw2grsL5C53bNXOdp5jbda5zysryHOaFZkn2JDNRnWDe3H5vQpytutWoTjATyr+ZuU99XJ3Lf94sUegbWbY6af6WJJ0r1jc9nbh1QtYQ/9NTdRpVWzysbEGqYoueRY9GtSNsz/UAtt/ZwvY3rKJv6l+sKL/BV96ur1dd8/H1qmS/2zMaPn0P0SUpnYHUGTmNmMZh2ORYxi9KDrnkpKtI9XX8N2b835nYPmJmHjXE+ni6aUQfW5dKJy/b9/OPNEt3Os1URlVnRHWVqz7GOW9H0vbmVPngjFfSr3V602nmoalxOuavTOCUbpq51Ew3rSXZb3W0rjVaZqKqS5H6vHSmQpeydUnzigmRTDJB1XDrzIGuwl1kZgI0mtn3699EH0//bhMWx+nj6UzzFBPgVSZ8GukVZqZ3c1P5a42y0kjq4+qMik7LvzBx1ulf3z/OeDNK3090Juf/PR6ZGYtEHja/j/4O+rN1lfp3a5L088FWi+cJUUWn6EShc/7fm7lpnXCai4nsaElknZm7HGJC+rmZSJrNHKvOWVbasCeRLWa8RjRbHaUTlc59/va58upjXRLVifVfn9XtXFE6sX9j5rb1jUO3h/UzE++j5k1AJ3ydKKufW82zReMAtgD9zBawQwpS//Z0IE3N7Xt1Znl8+2w/6xBsv8tetr9BFdvfsoK+GU82S6q6urHydo3ja2ZJc7xZKqu8vZLO7GlIKun7ynUf69JcIv9uXrvV9yv9Pg1Av+dD+dgsFerSpy6BtRRFZprITDNf60ymBvFQUdUw/9LMsL5inqc+hi7pRu9OlW03v5p+fc+U8mYSXZOjM6vZz9dpTANsi+qSbWZm4JlyrEd8Vf79s6hONKHU30l/R13lXR1VpY+vQT7m5TCdmR7xdSRLTah1hkPfHzTYugR6vPn9Kr9PafB1Otf3hG1mKVrfP/R9Qf8e+v9D3wdONjPluiSt/2+umhjJWvN3u/GTSP6qYok7z3o0qguWbxO1aOUOmb9sa/pZLVyxfe+/szFKx2T/1jGVX1fK7svu16/18+JVO/c+ZvYzKu/X8dn3Vv7sysfKxlfer19X3qY/J7tPb8sev9KuPW2yuzHYq/rr7LbK27N/Z7dX6+h92eNlt1X+u1L1/ZVjKn+X6r+Nyv6G2d8ku63yb6n3Zf+et3TLAeOyv1t2Xyb7nsqfdaj79f9H9u9sTPbvytuUPqfqn1c5tvLflb9bpcqfr5/18fTf2fjK78/G274v+3yo79Pb2j4d/rMR0mo+q8qvs/uzf2djbF9nt1V+7/6373/bvvtG/HzfvudQvt2YVPm8Rsiql6+Xxon37aW/j/4u+jn73bJ/Z7+3yn5fVfn7V8vuy+7Xr/VznqZ/lX1fdn/27+x75i/T16E+J71Pn8cWc5+O1edTvk8/V47Tz5Wy+yvvW2T+vdg8jn5e+PPX2b8r6ZjK+7Ovqy3Qx//539lYvU3HVz6G3pbR57N4lf69zPeZf2fPMfv90uep31txX6byd6h+jir7Ort/6eqde/+djVm8Sv/O5eegPyezxIzNfnYmG6OfK/+tYytvz2S/h/5bP+vjLTH/rnwe2df6WZ9P9jm7r/Lzob4vuy27fW9UsxdU9b8rX2AZ/VrfpPRz5Qu2cqx+ziYEpbdVvtAzlW/k2edqenv2eNnX1Z+zf+uY6ueU3Z7J7s9ilX2uDFb2deXt1Z+zf1feXvl1pvL2SnvHNLTu/Xq/29uR/V7Z769/S1u8Mtnvnd2nX1fep49VfZ/eVvn/Lfv+ynHZ49ruzz5X/ls/Z9+T3ZZFLxurX2fPp3Jcdlv2e+vnTDYuuy/7HtvnjI7V55L9jpX3Kb2t8nesHKefs9dvZdCy6Km9UUvpfeX7s8DtC132+cAIZ7cf6nurx++7b//AZla/coM0fnT/3qhW/k6V/9bPlf+vsq/19678u1SP1c/V/2/yNv3bvkf/nd2e3ZZFZG9MzJuofq4MTXZ79nUWUlV5e/ZvfSPOIjh/6eb0aw2dvknrbWn0Kj5Xy8ZW3q+Pk73RZ49TabH5fdL7sudgxmbPS/9d+Ttk9+ltGq5snN6v9PnqY2Uxyb7Wz5ns6/RnVvxbPy9ZrdOcvibMbSasC5bre5e+nvTr8t83ex6Z6ueWfZ3JxmX3Zd+Tfc6eZ/aclT4fDeGyNbsOuE/pbXp/FtHKcfq5/Hctj9Hblq7eKf8/bnUIO6ybMyUAAAAASUVORK5CYII=' // 图片

    const getCanvas = () => {
      let oCanvas = document.getElementById("myangle");
		  let canvFas = oCanvas.getContext("2d");
      oCanvas.style.background ='url(' + base64Img + ') no-repeat';
		  oCanvas.style.backgroundSize = '100% 100%';
      let image = new Image();
		  image.src = base64Img;
        image.onload = () => {
            oCanvas.width=image.width;
            oCanvas.height=image.height;
            canwidth = image.width;
            canheight = image.height;
            drawPoints(point1, point2, point3);
        }
    }
    const drawPoints = (point1, point2, point3) => {
      let canvas = document.getElementById("myangle");
      let ctx = canvas.getContext("2d");
      //获取屏幕分辨率
      // ctx.width = canwidth;
      // ctx.height=canheight;
      ctx.lineWidth = 2;
      ctx.strokeStyle = "red";
      ctx.fillStyle = "red";
      let sw = window.screen.width;
      let sh = window.screen.height - 140;
      if(point1.x > sw) {
          point1.x = sw;
      }
      if(point1.x < 0) {
          point1.x = 0;
      }
      if(point1.y > sh) {
          point1.y = sh;
      }
      if(point1.y < 43) {
          point1.y = 43;
      }
      if(point2.x > sw) {
          point2.x = sw;
      }
      if(point2.x < 0) {
          point2.x = 0;
      }
      if(point2.y > sh) {
          point2.y = sh;
      }
      if(point2.y < 43) {
          point2.y = 43;
      }
      if(point3.x > sw) {
          point3.x = sw;
      }
      if(point3.x < 0) {
          point3.x = 0;
      }
      if(point3.y > sh) {
          point3.y = sh;
      }
      if(point3.y < 43) {
          point3.y = 43;
      }
      ctx.setLineDash([0]); //设置虚线间距
      // 画点
      ctx.beginPath();
      ctx.arc(point1.x, point1.y, cPointSize, 0, 2 * Math.PI);
      //ctx.stroke();//空心圆
      ctx.fill(); //实心圆
      ctx.font = "20px";
      //ctx.strokeText("(" + point1.x + ", " + 　point1.y + ")", (point1.x - cPointSize), (point1.y - cPointSize));
      ctx.beginPath();
      ctx.arc(point2.x, point2.y, cPointSize, 0, 2 * Math.PI);
      ctx.fill();
      ctx.font = "20px";
      // ctx.strokeText("(" + point2.x + ", " + 　point2.y + ")", (point2.x - cPointSize), (point2.y - cPointSize));
      ctx.beginPath();
      ctx.arc(point3.x, point3.y, cPointSize, 0, 2 * Math.PI);
      ctx.fill();
      ctx.font = "20px";
      // ctx.strokeText("(" + point3.x + ", " + 　point3.y + ")", (point3.x - cPointSize), (point3.y - cPointSize));
      ctx.setLineDash([5, 10]); //设置虚线间距
      ctx.beginPath();
      ctx.moveTo(point1.x, point1.y);
      ctx.lineTo(point2.x, point2.y);
      ctx.lineCap = "round";
      ctx.stroke();
      ctx.beginPath();
      ctx.moveTo(point1.x, point1.y);
      ctx.lineTo(point3.x, point3.y);
      ctx.lineCap = "round";
      ctx.stroke();
      computeAngle(point1, point2, point3)
      ctx.font="16px Arial";
      ctx.fillText('角度:'+ angle,20,30);
    }
    // 计算getBoundingClientRect
    const getOffsetPosition = (elem) =>{
      if ( !elem ) return {left:0, top:0};
      let top = 0, left = 0;
      if ( "getBoundingClientRect" in document.documentElement ){
        let box = elem.getBoundingClientRect(), 
        doc = elem.ownerDocument, 
        body = doc.body, 
        docElem = doc.documentElement,
        clientTop = docElem.clientTop || body.clientTop || 0, 
        clientLeft = docElem.clientLeft || body.clientLeft || 0,
        top  = box.top  + (self.pageYOffset || docElem && docElem.scrollTop  || body.scrollTop ) - clientTop,
        left = box.left + (self.pageXOffset || docElem && docElem.scrollLeft || body.scrollLeft) - clientLeft;
      }else{
        do{
          top += elem.offsetTop || 0;
          left += elem.offsetLeft || 0;
          elem = elem.offsetParent;
        } while (elem);
      }
      return {left:left, top:top};    
    }
    //开始画图
    const movestart = (ev) => {
      let canvas = document.getElementById("myangle");
      let { left, top } = getOffsetPosition(canvas)
      var e = ev || event;
      startX = e.touches[0].pageX - left;
      startY = e.touches[0].pageY - top;
      drag(Math.ceil(startX), Math.ceil(startY));
    }
    var canvas = document.getElementById("myangle")
    canvas.addEventListener("touchstart", movestart);
    //拖拽函数
    const drag = (x, y) => {
      let canvas = document.getElementById("myangle");
      let range = 30;
      if(x >= point1.x - range && x <= point1.x + range && y >= point1.y - range && y <= point1.y + range) {
          dragPoint = point1
      } else if(x >= point2.x - range && x <= point2.x + range && y >= point2.y - range && y <= point2.y + range) {
          dragPoint = point2
      } else if(x >= point3.x - range && x <= point3.x + range && y >= point3.y - range && y <= point3.y + range) {
          dragPoint = point3
      }
      if(dragPoint) {
          canvas.addEventListener("touchmove", moveing, false);
          //鼠标移开事件
          canvas.addEventListener("touchend", touchScroll);
      }
    }
    //画图中
    const moveing = (ev) => {
      let canvas = document.getElementById("myangle");
      let ctx = canvas.getContext("2d");
      var e = ev || event;
      e.preventDefault();
      let { left, top } = getOffsetPosition(canvas)
      let ax = e.touches[0].pageX - Math.ceil(left)
      let ay = e.touches[0].pageY - Math.ceil(top)
      dragPoint.x = dragPoint.x + (ax - startX)
      dragPoint.y = dragPoint.y + (ay - startY)
      startX = ax;
      startY = ay;
      //鼠标移动每一帧都清楚画布内容，然后重新画圆
      ctx.clearRect(0, 0, canvas.width, canvas.height);
      drawPoints(point1, point2, point3)
    }
    const touchScroll = () => {
      let canvas = document.getElementById("myangle");
      canvas.removeEventListener("touchmove", moveing, false);
    }
    // 计算角度
    const computeAngle = (point1, point2, point3) => {
      let line12 = Math.sqrt(Math.pow(Math.abs(point2.x - point1.x), 2) + Math.pow(Math.abs(point2.y - point1.y), 2))
      let line13 = Math.sqrt(Math.pow(Math.abs(point3.x - point1.x), 2) + Math.pow(Math.abs(point3.y - point1.y), 2))
      let line23 = Math.sqrt(Math.pow(Math.abs(point3.x - point2.x), 2) + Math.pow(Math.abs(point3.y - point2.y), 2))
      // 勾股定理求角度
      var angle1 = 360 * Math.acos((Math.pow(line12, 2) + Math.pow(line13, 2) - Math.pow(line23, 2)) / (2 * line12 * line13)) / (2 * Math.PI)
      angle = angle1.toFixed(1);
      console.log('angle', angle);
    }
    getCanvas()
  </script>
</body>
</html>
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/小蓝xlanll/article/detail/266584