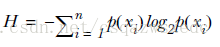- 1The Node.js path can contain only letters,digits,periods(.),underscores(_), hyphens (-), colon (:) a_鸿蒙 dev安装 the node.js path can contain only letters
- 2云计算机是什么样子,云电脑的配置怎么样?高配与标配的区别是什么?
- 3imx6ull - 制作烧录SD卡
- 4使用Python发送电子邮件
- 5root用户启动beeline时报错User: root is not allowed to impersonate root (state=,code=0)_不能用root进入beeline
- 6基于canvas画布的实用类Fabric.js的使用Part.2
- 7一骑绝尘!BEV-LaneDet:暴涨十个点,单目3D车道线新SOTA!
- 8nginx配置域名和ip_nginx配置域名和ip都能访问
- 9windows凭据收集_mimikatz获取凭据密码
- 10【无标题】人工智能_人工智能的研究背景
决策树原理实例(python代码实现)_决策树python代码
赞
踩
决策数(Decision Tree)在机器学习中也是比较常见的一种算法,属于监督学习中的一种。看字面意思应该也比较容易理解,相比其他算法比如支持向量机(SVM)或神经网络,似乎决策树感觉“亲切”许多。
- 优点:计算复杂度不高,输出结果易于理解,对中间值的缺失值不敏感,可以处理不相关特征数据。
- 缺点:可能会产生过度匹配的问题。
- 使用数据类型:数值型和标称型。
简单介绍完毕,让我们来通过一个例子让决策树“原形毕露”。
一天,老师问了个问题,只根据头发和声音怎么判断一位同学的性别。
为了解决这个问题,同学们马上简单的统计了7位同学的相关特征,数据如下:
| 头发 | 声音 | 性别 |
|---|---|---|
| 长 | 粗 | 男 |
| 短 | 粗 | 男 |
| 短 | 粗 | 男 |
| 长 | 细 | 女 |
| 短 | 细 | 女 |
| 短 | 粗 | 女 |
| 长 | 粗 | 女 |
| 长 | 粗 | 女 |
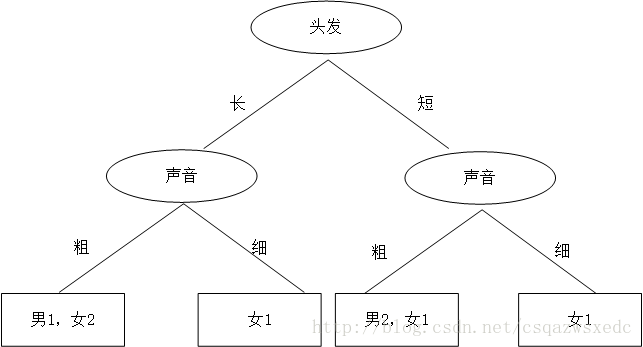
机智的同学A想了想,先根据头发判断,若判断不出,再根据声音判断,于是画了一幅图,如下:
于是,一个简单、直观的决策树就这么出来了。头发长、声音粗就是男生;头发长、声音细就是女生;头发短、声音粗是男生;头发短、声音细是女生。
原来机器学习中决策树就这玩意,这也太简单了吧。。。
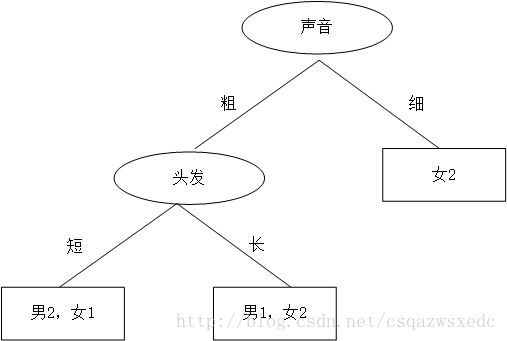
这时又蹦出个同学B,想先根据声音判断,然后再根据头发来判断,如是大手一挥也画了个决策树:
同学B的决策树:首先判断声音,声音细,就是女生;声音粗、头发长是男生;声音粗、头发长是女生。
那么问题来了:同学A和同学B谁的决策树好些?计算机做决策树的时候,面对多个特征,该如何选哪个特征为最佳的划分特征?
划分数据集的大原则是:将无序的数据变得更加有序。
我们可以使用多种方法划分数据集,但是每种方法都有各自的优缺点。于是我们这么想,如果我们能测量数据的复杂度,对比按不同特征分类后的数据复杂度,若按某一特征分类后复杂度减少的更多,那么这个特征即为最佳分类特征。
Claude Shannon 定义了熵(entropy)和信息增益(information gain)。
用熵来表示信息的复杂度,熵越大,则信息越复杂。公式如下:
信息增益(information gain),表示两个信息熵的差值。
首先计算未分类前的熵,总共有8位同学,男生3位,女生5位。
熵(总)=-3/8log2(3/8)-5/8log2(5/8)=0.9544
接着分别计算同学A和同学B分类后信息熵。
同学A首先按头发分类,分类后的结果为:长头发中有1男3女。短头发中有2男2女。
熵(同学A长发)=-1/4log2(1/4)-3/4log2(3/4)=0.8113
熵(同学A短发)=-2/4log2(2/4)-2/4log2(2/4)=1
熵(同学A)=4/80.8113+4/81=0.9057
信息增益(同学A)=熵(总)-熵(同学A)=0.9544-0.9057=0.0487
同理,按同学B的方法,首先按声音特征来分,分类后的结果为:声音粗中有3男3女。声音细中有0男2女。
熵(同学B声音粗)=-3/6log2(3/6)-3/6log2(3/6)=1
熵(同学B声音粗)=-2/2log2(2/2)=0
熵(同学B)=6/81+2/8*0=0.75
信息增益(同学B)=熵(总)-熵(同学B)=0.9544-0.75=0.2087
按同学B的方法,先按声音特征分类,信息增益更大,区分样本的能力更强,更具有代表性。
以上就是决策树ID3算法的核心思想。
接下来用python代码来实现ID3算法:
from math import log import operator def calcShannonEnt(dataSet): # 计算数据的熵(entropy) numEntries=len(dataSet) # 数据条数 labelCounts={} for featVec in dataSet: currentLabel=featVec[-1] # 每行数据的最后一个字(类别) if currentLabel not in labelCounts.keys(): labelCounts[currentLabel]=0 labelCounts[currentLabel]+=1 # 统计有多少个类以及每个类的数量 shannonEnt=0 for key in labelCounts: prob=float(labelCounts[key])/numEntries # 计算单个类的熵值 shannonEnt-=prob*log(prob,2) # 累加每个类的熵值 return shannonEnt def createDataSet1(): # 创造示例数据 dataSet = [['长', '粗', '男'], ['短', '粗', '男'], ['短', '粗', '男'], ['长', '细', '女'], ['短', '细', '女'], ['短', '粗', '女'], ['长', '粗', '女'], ['长', '粗', '女']] labels = ['头发','声音'] #两个特征 return dataSet,labels def splitDataSet(dataSet,axis,value): # 按某个特征分类后的数据 retDataSet=[] for featVec in dataSet: if featVec[axis]==value: reducedFeatVec =featVec[:axis] reducedFeatVec.extend(featVec[axis+1:]) retDataSet.append(reducedFeatVec) return retDataSet def chooseBestFeatureToSplit(dataSet): # 选择最优的分类特征 numFeatures = len(dataSet[0])-1 baseEntropy = calcShannonEnt(dataSet) # 原始的熵 bestInfoGain = 0 bestFeature = -1 for i in range(numFeatures): featList = [example[i] for example in dataSet] uniqueVals = set(featList) newEntropy = 0 for value in uniqueVals: subDataSet = splitDataSet(dataSet,i,value) prob =len(subDataSet)/float(len(dataSet)) newEntropy +=prob*calcShannonEnt(subDataSet) # 按特征分类后的熵 infoGain = baseEntropy - newEntropy # 原始熵与按特征分类后的熵的差值 if (infoGain>bestInfoGain): # 若按某特征划分后,熵值减少的最大,则次特征为最优分类特征 bestInfoGain=infoGain bestFeature = i return bestFeature def majorityCnt(classList): #按分类后类别数量排序,比如:最后分类为2男1女,则判定为男; classCount={} for vote in classList: if vote not in classCount.keys(): classCount[vote]=0 classCount[vote]+=1 sortedClassCount = sorted(classCount.items(),key=operator.itemgetter(1),reverse=True) return sortedClassCount[0][0] def createTree(dataSet,labels): classList=[example[-1] for example in dataSet] # 类别:男或女 if classList.count(classList[0])==len(classList): return classList[0] if len(dataSet[0])==1: return majorityCnt(classList) bestFeat=chooseBestFeatureToSplit(dataSet) #选择最优特征 bestFeatLabel=labels[bestFeat] myTree={bestFeatLabel:{}} #分类结果以字典形式保存 del(labels[bestFeat]) featValues=[example[bestFeat] for example in dataSet] uniqueVals=set(featValues) for value in uniqueVals: subLabels=labels[:] myTree[bestFeatLabel][value]=createTree(splitDataSet\ (dataSet,bestFeat,value),subLabels) return myTree if __name__=='__main__': dataSet, labels=createDataSet1() # 创造示列数据 print(createTree(dataSet, labels)) # 输出决策树模型结果
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
输出结果为:
{'声音': {'细': '女', '粗': {'头发': {'短': '男', '长': '女'}}}}
- 1
这个结果的意思是:首先按声音分类,声音细为女生;然后再按头发分类:声音粗,头发短为男生;声音粗,头发长为女生。
这个结果也正是同学B的结果。
补充说明:判定分类结束的依据是,若按某特征分类后出现了最终类(男或女),则判定分类结束。使用这种方法,在数据比较大,特征比较多的情况下,很容易造成过拟合,于是需进行决策树枝剪,一般枝剪方法是当按某一特征分类后的熵小于设定值时,停止分类。
ID3算法存在的缺点:
- ID3算法在选择根节点和内部节点中的分支属性时,采用信息增益作为评价标准。信息增益的缺点是倾向于选择取值较多是属性,在有些情况下这类属性可能不会提供太多有价值的信息。
- ID3算法只能对描述属性为离散型属性的数据集构造决策树 。
为了改进决策树,又提出了ID4.5算法和CART算法。之后有时间会介绍这两种算法。
参考: