【视频】Lasso回归、岭回归等正则化回归数学原理及R语言实例_岭回归、lasso回归、决策树回归、随机森林回归实现一遍并且得到r方

最近我们被客户要求撰写关于正则化回归的研究报告，包括一些图形和统计输出。

在本视频中，我们将介绍Lasso套索回归、岭回归等正则化的回归方法的数学原理以及R软件实例。

视频：Lasso回归、岭回归正则化回归数学原理及R软件实例

，时长13:27

为什么要LASSO套索回归？

套索可以通过选择最小化预测误差的变量子集来帮助选择与结果相关的变量简约子集。

选择模型取决于数据集和您正在处理的问题陈述。了解数据集以及特征如何相互交互至关重要。 

当我们增加回归模型的自由度（增加方程中的多项式），预测变量可能高度相关，多重共线性可能会成为一个问题。这可能导致模型的系数估计不可靠并且具有高方差。也就是说，当模型被应用到以前从未见过的新数据集时，它的表现可能会很差。

有许多独立变量或预测变量，以至于调查人员无法将所有预测变量放入模型中，或者可能怀疑许多变量与我们有兴趣预测的结果无关。

因此，如果数据集具有高维度和高相关性，则可以使用套索回归。

套索回归会惩罚数据集中不太重要的特征，并使它们各自的系数为零，从而消除它们。因此，它为您提供了特征选择和简单模型创建的好处。 

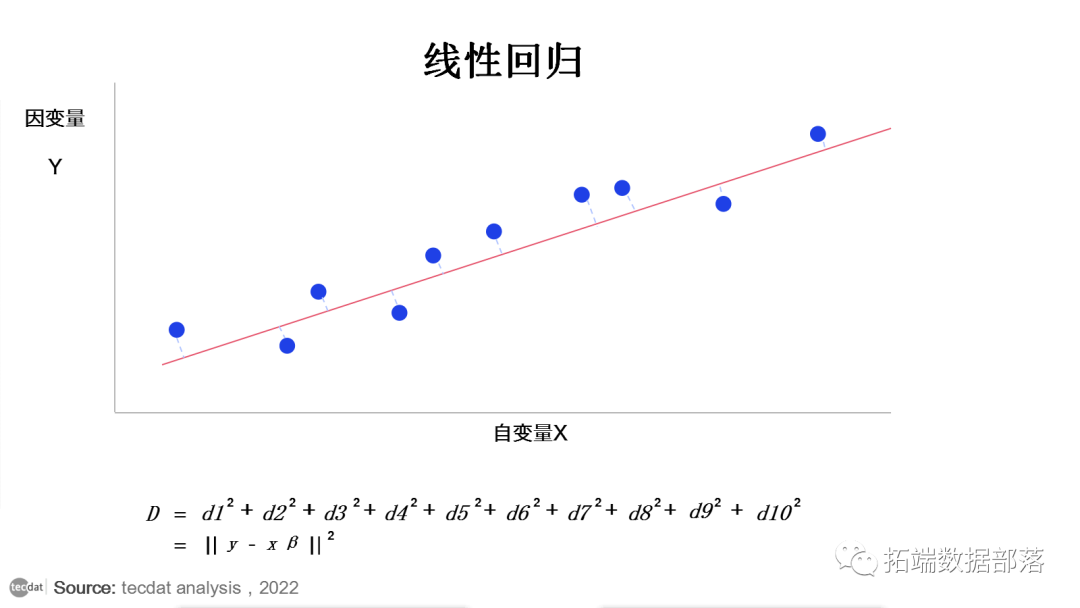
在我们进一步讨论套索之前，让我们回顾一下回归。

什么是回归？

回归是一种统计技术，用于确定一个因变量与一个或多个自变量之间的关系。简而言之，回归分析将告诉您结果如何因不同因素而变化。 

例如，什么决定了一个人的薪水？

许多因素，如学历、经验、技能、工作角色、公司等，都会对薪酬产生影响。 

您可以使用回归分析来预测因变量。 

Y等于m乘以x加c

你还记得我们学生时代的这个方程式吗？ 

它只不过是一个线性回归方程。在上述等式中，因变量估计自变量。

用数学术语来说， 

·Y 是依赖值， 

·X 是独立值，

·m 是直线的斜率，

·c 是常数值。

在机器学习 或统计世界中，相同的方程项的名称略有不同 。

·Y 是 预测 值， 

·X是 特征 值，

·m 是  系数 或权重，

·c 是 偏差值。

 在普通最小 二乘法方法中，我们将残差的平方和尽可能小。换句话说，我们最小化损失函数：

如果用d表示图中实际数据点与模型线的距离。

损失函数可以用点之间距离的平方和来表示

在线性回归中，以最小 二乘最小化的方式选择最佳模型。

同时也获得了OLS参数估计

 在统计学中，需要考虑估计量的两个关键特征：偏差和方差。偏差是真实总体参数和预期估计量之间的差异：

它衡量估计的准确性。另一方面，方差衡量这些估计中的分布或不确定性。

其中未知误差方差σ 平方可以从残差估计为

偏差和方差都希望很低，因为较大的值会导致模型的预测不佳。

 下图说明了偏差和方差是什么。想象一下，靶心是我们正在估计的真实参数β，它的镜头是我们的估计值，这些估计值是由四个不同的估计量得出的——偏差和方差，以及它们的组合。

 事实上，模型的误差可以分解为三个部分：大方差导致的误差、显著偏差导致的误差以及剩下的——无法解释的部分。

 由于过度拟合，该模型将具有低偏差和高方差。模型拟合在训练数据中很好，但它不会给出很好的测试数据预测。

 当预测变量高度相关时，多重共线性可能会成为一个问题。这可能导致模型的系数估计不可靠并且具有高方差。

·有很多预测因素。这反映在上面给出的方差公式中：方差接近无穷大。

 正则化开始发挥作用来解决这个问题。

什么是正则化？

正则化解决了过拟合的问题。它将这些错误学习的系数缩小为零。

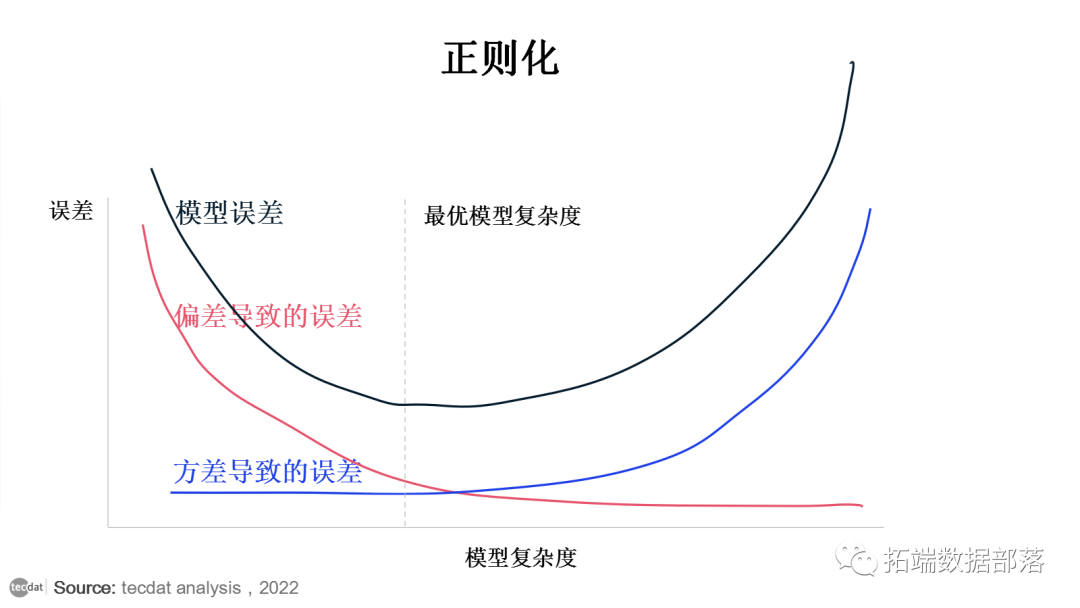
正则化的一般解决方案是：以引入一些偏差为代价减少方差。这种方法几乎总是有利于模型的预测性能。让我们看一下下面的图。

随着模型复杂性的增加（也就是在线性回归的情况下可以被认为是预测变量的数量），估计的方差也会增加，但偏差会减少。无偏的 OLS 会将我们置于图片的右侧，这远非最优。这就是我们进行正则化的原因：最小化变量的数量，降低模型的复杂度的同时，以一些偏差为代价来降低方差，从而在图上向左移动，向最优方向移动。 

套索回归

套索回归类似于线性回归，但它使用了一种“收缩”技术，其中决定系数向零收缩。 

套索回归允许您缩小或正则化这些系数以避免过拟合，并使它们在不同的数据集上更好地工作。 

d1、d2、d3等，表示上图中实际数据点与模型线的距离。 

最小二乘是绘制曲线 的点之间距离的平方和。

在线性回归中，以最小二乘 最小化的方式选择最佳模型。

在执行 套索回归时，我们在最小二乘中添加了一个惩罚因子。也就是说，模型的选择方式是将以下损失函数降低到最小值。

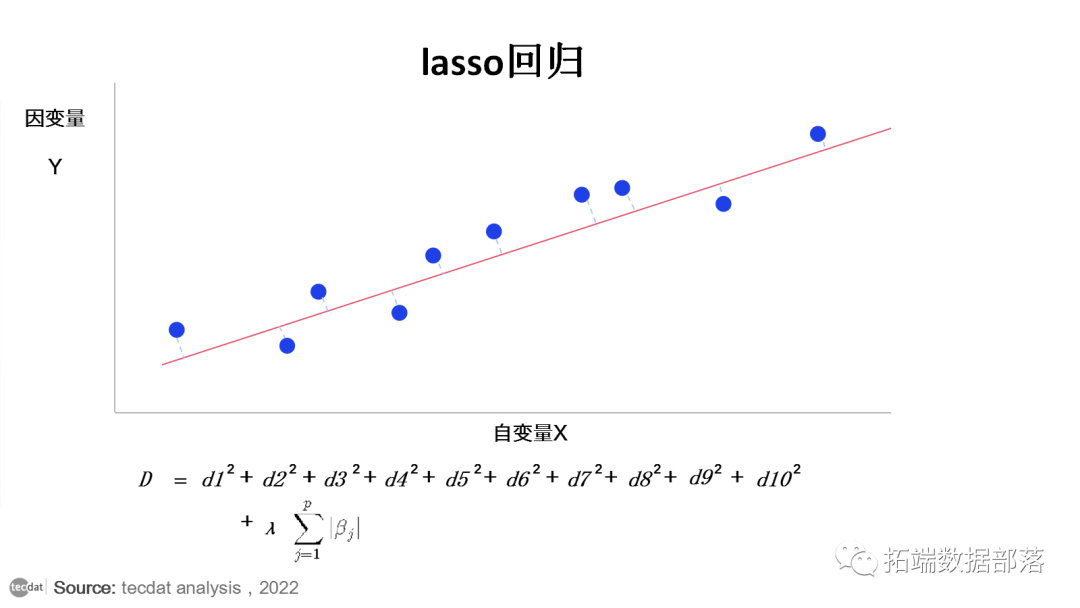
D 等于 最小二乘 加上 lambda 乘以 （系数大小的绝对值）的总和

套索回归惩罚由所有估计的参数组成。Lambda 可以是零到无穷大之间的任何值。该值决定了执行正则化的积极程度。通常使用交叉验证来选择它。 

套索惩罚系数的绝对值之和。当 λ 等于零时，模型变为普通最小二乘回归。随着 lambda 值的增加，系数减小并最终变为零。通过这种方式，套索回归从我们的模型中消除了无关紧要的变量。 尽管，我们的正则化模型的偏差可能比线性回归略高，但对未来预测的方差较小，解决了过拟合问题。

套索回归和岭回归都被称为 正则化方法，因为它们都试图最小化残差平方和 (RSS) 以及一些惩罚项。

换句话说，它们约束或 规范模型的系数估计。

但是，他们使用的惩罚有点不同：

套索回归试图最小化RSS + λΣ|β j |

岭回归试图最小化RSS + λΣβ j 的平方

当我们使用岭回归时，每个预测变量的系数都缩小到零，但没有一个可以 完全归零。

相反，当我们使用 套索回归时，当 λ 变得足够大时，一些系数可能会 完全变为零。

用技术术语来说，套索回归能够产生“稀疏”模型——模型只包含预测变量的一个子集。

这就引出了一个问题：岭回归还是套索回归更好？

答案是：视情况而定！

在只有少数预测变量显著的情况下，套索回归往往表现更好，因为它能够将不显著的变量完全缩小为零并将它们从模型中删除。

然而，当许多预测变量在模型中很重要并且它们的系数大致相等时，岭回归往往会表现得更好，因为它将所有预测变量都保留在模型中。

接下来我们在r语言中建立套索回归，ridge岭回归和elastic-net模型：

r语言中对LASSO回归，Ridge岭回归和弹性网络Elastic Net模型实现

Glmnet是一个通过惩罚最大似然关系拟合广义线性模型的软件包。正则化路径是针对正则化参数λ的值网格处的lasso或Elastic Net（弹性网络）惩罚值计算的。该算法非常快，并且可以利用输入矩阵中的稀疏性 x。它适合线性，逻辑和多项式，泊松和Cox回归模型。可以从拟合模型中做出各种预测。它也可以拟合多元线性回归。

glmnet 解决以下问题

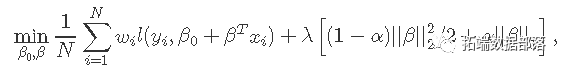
在覆盖整个范围的λ值网格上。这里l（y，η）是观察i的负对数似然贡献；例如对于高斯分布是

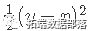
。 _弹性网络_惩罚由α控制，LASSO（α= 1，默认），Ridge（α= 0）。调整参数λ控制惩罚的总强度。

众所周知，岭惩罚使相关预测因子的系数彼此缩小，而套索倾向于选择其中一个而丢弃其他预测因子。_弹性网络_则将这两者混合在一起。

glmnet 算法使用循环坐标下降法，该方法在每个参数固定不变的情况下连续优化目标函数，并反复循环直到收敛，我们的算法可以非常快速地计算求解路径。

代码可以处理稀疏的输入矩阵格式，以及系数的范围约束，还包括用于预测和绘图的方法，以及执行K折交叉验证的功能。

快速开始

首先，我们加载 glmnet 包：

library(glmnet)

包中使用的默认模型是高斯线性模型或“最小二乘”。我们加载一组预先创建的数据以进行说明。用户可以加载自己的数据，也可以使用工作空间中保存的数据。

该命令 从此保存的R数据中加载输入矩阵 x 和因向量 y。

我们拟合模型 glmnet。

fit = glmnet(x, y)

可以通过执行plot 函数来可视化系数 ：

plot(fit)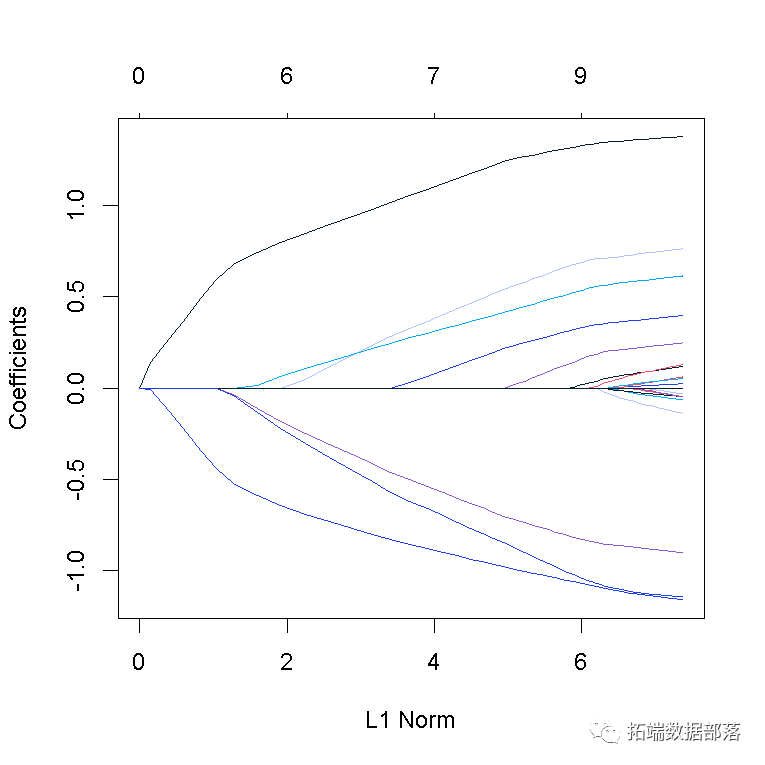

每条曲线对应一个变量。它显示了当λ变化时，其系数相对于整个系数向量的ℓ1范数的路径。上方的轴表示当前λ处非零系数的数量，这是套索的有效自由度（_df_）。用户可能还希望对曲线进行注释。这可以通过label = TRUE 在plot命令中进行设置来完成 。

glmnet 如果我们只是输入对象名称或使用print 函数，则会显示每个步骤的路径 摘要 ：

print(fit)

## 
## Call:  glmnet(x = x, y = y) 
## 
##       Df   %Dev  Lambda
##  \[1,\]  0 0.0000 1.63000
##  \[2,\]  2 0.0553 1.49000
##  \[3,\]  2 0.1460 1.35000
##  \[4,\]  2 0.2210 1.23000
##  \[5,\]  2 0.2840 1.12000
##  \[6,\]  2 0.3350 1.02000
##  \[7,\]  4 0.3900 0.93300
##  \[8,\]  5 0.4560 0.85000
##  \[9,\]  5 0.5150 0.77500
## \[10,\]  6 0.5740 0.70600
## \[11,\]  6 0.6260 0.64300
## \[12,\]  6 0.6690 0.58600
## \[13,\]  6 0.7050 0.53400
## \[14,\]  6 0.7340 0.48700
## \[15,\]  7 0.7620 0.44300
## \[16,\]  7 0.7860 0.40400
## \[17,\]  7 0.8050 0.36800
## \[18,\]  7 0.8220 0.33500
## \[19,\]  7 0.8350 0.30600
## \[20,\]  7 0.8460 0.27800

它从左到右显示了非零系数的数量（Df），解释的（零）偏差百分比（%dev）和λ（Lambda）的值。

我们可以在序列范围内获得一个或多个λ处的实际系数：

coef(fit,s=0.1)

## 21 x 1 sparse Matrix of class "dgCMatrix"
##                     1
## (Intercept)  0.150928
## V1           1.320597
## V2           .       
## V3           0.675110
## V4           .       
## V5          -0.817412
## V6           0.521437
## V7           0.004829
## V8           0.319416
## V9           .       
## V10          .       
## V11          0.142499
## V12          .       
## V13          .       
## V14         -1.059979
## V15          .       
## V16          .       
## V17          .       
## V18          .       
## V19          .       
## V20         -1.021874

还可以使用新的输入数据在特定的λ处进行预测：

predict(fit,newx=nx,s=c(0.1,0.05))

##             1       2
##  \[1,\]  4.4641  4.7001
##  \[2,\]  1.7509  1.8513
##  \[3,\]  4.5207  4.6512
##  \[4,\] -0.6184 -0.6764
##  \[5,\]  1.7302  1.8451
##  \[6,\]  0.3565  0.3512
##  \[7,\]  0.2881  0.2662
##  \[8,\]  2.7776  2.8209
##  \[9,\] -3.7016 -3.7773
## \[10,\]  1.1546  1.1067

该函数 glmnet 返回一系列模型供用户选择。交叉验证可能是该任务最简单，使用最广泛的方法。

cv.glmnet 是交叉验证的主要函数。

cv.glmnet 返回一个 cv.glmnet 对象，此处为“ cvfit”，其中包含交叉验证拟合的所有成分的列表。

我们可以绘制对象。

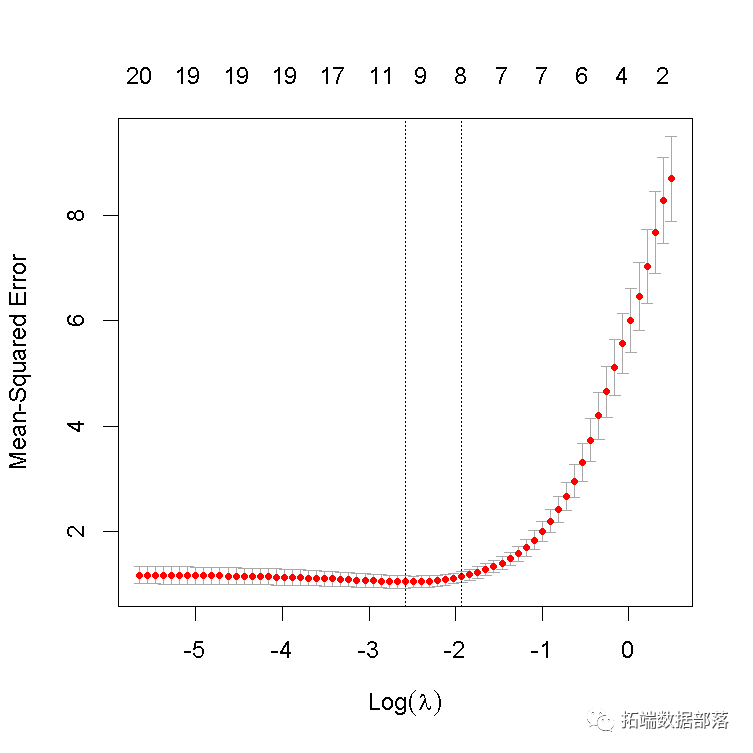
它包括交叉验证曲线（红色虚线）和沿λ序列的上下标准偏差曲线（误差线）。垂直虚线表示两个选定的λ。

我们可以查看所选的λ和相应的系数。例如，

cvfit$lambda.min

## \[1\] 0.08307

lambda.min 是给出最小平均交叉验证误差的λ值。保存的另一个λ是 lambda.1se，它给出了的模型，使得误差在最小值的一个标准误差以内。我们只需要更换 lambda.min 到lambda.1se 以上。

coef(cvfit, s = "lambda.min")

## 21 x 1 sparse Matrix of class "dgCMatrix"
##                    1
## (Intercept)  0.14936
## V1           1.32975
## V2           .      
## V3           0.69096
## V4           .      
## V5          -0.83123
## V6           0.53670
## V7           0.02005
## V8           0.33194
## V9           .      
## V10          .      
## V11          0.16239
## V12          .      
## V13          .      
## V14         -1.07081
## V15          .      
## V16          .      
## V17          .      
## V18          .      
## V19          .      
## V20         -1.04341

注意，系数以稀疏矩阵格式表示。原因是沿着正则化路径的解通常是稀疏的，因此使用稀疏格式在时间和空间上更为有效。

可以根据拟合的cv.glmnet 对象进行预测 。让我们看一个示例。

##            1
## \[1,\] -1.3647
## \[2,\]  2.5686
## \[3,\]  0.5706
## \[4,\]  1.9682
## \[5,\]  1.4964

newx 与新的输入矩阵 s相同，如前所述，是预测的λ值。

线性回归

这里的线性回归是指两个模型系列。一个是 gaussian正态_分布_，另一个是 mgaussian多元正态_分布_。

正态_分布_

假设我们有观测值xi∈Rp并且yi∈R，i = 1，...，N。目标函数是

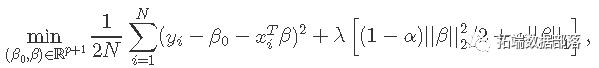
其中λ≥0是复杂度参数，0≤α≤1在岭回归（α=0）和套索LASSO（α=1）之间。

应用坐标下降法解决该问题。具体地说，通过计算βj=β〜j处的梯度和简单的演算，更新为

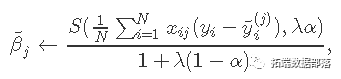
其中

。

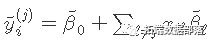
当x 变量标准化为具有单位方差（默认值）时，以上公式适用 。

glmnet 提供各种选项供用户自定义。我们在这里介绍一些常用的选项，它们可以在glmnet 函数中指定 。

• alpha 表示弹性网混合参数α，范围α∈[0,1]。α=1是套索（默认），α=0是Ridge。

• weights 用于观察权重。每个观察值的默认值为1。

• nlambda 是序列中λ值的数量。默认值为100。

• lambda 可以提供，但通常不提供，程序会构建一个序列。自动生成时，λ序列由lambda.max 和 确定 lambda.min.ratio。

• standardize 是x 在拟合模型序列之前进行变量标准化的逻辑标志 。

例如，我们设置α=0.2，并对后半部分的观测值赋予两倍的权重。为了避免在此处显示太长时间，我们将其设置 nlambda 为20。但是，实际上，建议将λ的数量设置为100（默认值）或更多。

然后我们可以输出glmnet 对象。

print(fit)

## 
## Call:  glmnet(x = x, y = y, weights = c(rep(1, 50), rep(2, 50)), alpha = 0.2,      nlambda = 20) 
## 
##       Df  %Dev  Lambda
##  \[1,\]  0 0.000 7.94000
##  \[2,\]  4 0.179 4.89000
##  \[3,\]  7 0.444 3.01000
##  \[4,\]  7 0.657 1.85000
##  \[5,\]  8 0.785 1.14000
##  \[6,\]  9 0.854 0.70300
##  \[7,\] 10 0.887 0.43300
##  \[8,\] 11 0.902 0.26700
##  \[9,\] 14 0.910 0.16400
## \[10,\] 17 0.914 0.10100
## \[11,\] 17 0.915 0.06230
## \[12,\] 17 0.916 0.03840
## \[13,\] 19 0.916 0.02360
## \[14,\] 20 0.916 0.01460
## \[15,\] 20 0.916 0.00896
## \[16,\] 20 0.916 0.00552
## \[17,\] 20 0.916 0.00340

这将显示生成对象的调用 fit 以及带有列Df （非零系数的数量），  %dev （解释的偏差百分比）和Lambda （对应的λ值） 的三列矩阵 。

我们可以绘制拟合的对象。

让我们针对log-lambda值标记每个曲线来绘制“拟合”。

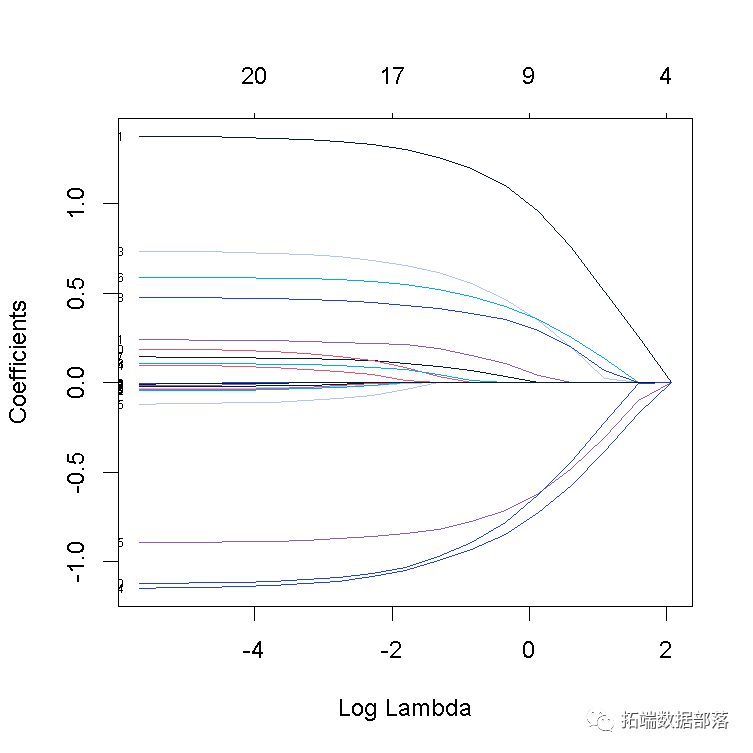
这是训练数据中的偏差百分比。我们在这里看到的是，在路径末端时，该值变化不大，但是系数有点“膨胀”。这使我们可以将注意力集中在重要的拟合部分上。

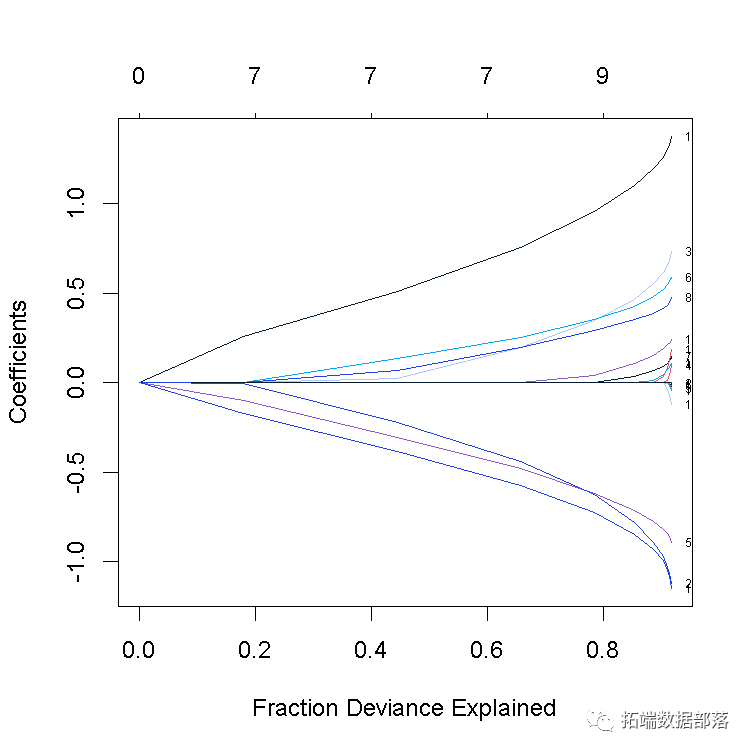
我们可以提取系数并在某些特定值的情况下进行预测。两种常用的选项是：

• s 指定进行提取的λ值。

• exact 指示是否需要系数的精确值。

一个简单的例子是：

## 21 x 2 sparse Matrix of class "dgCMatrix"
##                    1         1
## (Intercept)  0.19657  0.199099
## V1           1.17496  1.174650
## V2           .        .       
## V3           0.52934  0.531935
## V4           .        .       
## V5          -0.76126 -0.760959
## V6           0.46627  0.468209
## V7           0.06148  0.061927
## V8           0.38049  0.380301
## V9           .        .       
## V10          .        .       
## V11          0.14214  0.143261
## V12          .        .       
## V13          .        .       
## V14         -0.91090 -0.911207
## V15          .        .       
## V16          .        .       
## V17          .        .       
## V18          .        0.009197
## V19          .        .       
## V20         -0.86099 -0.863117

左列是，exact = TRUE 右列是 FALSE。从上面我们可以看到，0.01不在序列中，因此尽管没有太大差异，但还是有一些差异。如果没有特殊要求，则线性插补就足够了。

用户可以根据拟合的对象进行预测。除中的选项外 coef，主要参数是 newx的新值矩阵 x。type 选项允许用户选择预测类型：*“链接”给出拟合值

• 因变量与正态分布的“链接”相同。

• “系数”计算值为的系数 s

例如，

##            1
## \[1,\] -0.9803
## \[2,\]  2.2992
## \[3,\]  0.6011
## \[4,\]  2.3573
## \[5,\]  1.7520

给出在λ=0.05时前5个观测值的拟合值。如果提供的多个值， s 则会生成预测矩阵。

用户可以自定义K折交叉验证。除所有 glmnet 参数外， cv.glmnet 还有特殊的参数，包括 nfolds （次数），  foldid （用户提供的次数），  type.measure（用于交叉验证的损失）：*“ deviance”或“ mse”

• “ mae”使用平均绝对误差

举个例子，

cvfit = cv.glmnet(x, y, type.measure = "mse", nfolds = 20)

根据均方误差标准进行20折交叉验证。

并行计算也受 cv.glmnet。为我们在这里给出一个简单的比较示例。

system.time(cv.glmnet(X, Y))

##    user  system elapsed 
##   3.591   0.103   3.724

system.time(cv.glmnet(X, Y, parallel = TRUE))

##    user  system elapsed 
##   4.318   0.391   2.700

从上面的建议可以看出，并行计算可以大大加快计算过程。

• “ lambda.min”：达到最小MSE的λ。

cvfit$lambda.min

## \[1\] 0.08307

## 21 x 1 sparse Matrix of class "dgCMatrix"
##                    1
## (Intercept)  0.14936
## V1           1.32975
## V2           .      
## V3           0.69096
## V4           .      
## V5          -0.83123
## V6           0.53670
## V7           0.02005
## V8           0.33194
## V9           .      
## V10          .      
## V11          0.16239
## V12          .      
## V13          .      
## V14         -1.07081
## V15          .      
## V16          .      
## V17          .      
## V18          .      
## V19          .      
## V20         -1.04341

在这里，我们使用相同的k折，为α选择一个值。

将它们全部放置在同一绘图上：

我们看到lasso（alpha=1）在这里表现最好。

系数上下限

假设我们要拟合我们的模型，但将系数限制为大于-0.7且小于0.5。这可以通过upper.limits 和 lower.limits 参数实现 ：

通常，我们希望系数为正，因此我们只能lower.limit 将其设置 为0。

惩罚因素

此参数允许用户将单独的惩罚因子应用于每个系数。每个参数的默认值为1，但可以指定其他值。特别是，任何penalty.factor 等于零的变量 都不会受到惩罚

在许多情况下，某些变量可能是重要，我们希望一直保留它们，这可以通过将相应的惩罚因子设置为0来实现：

我们从标签中看到惩罚因子为0的三个变量始终保留在模型中，而其他变量遵循典型的正则化路径并最终缩小为0。

自定义图

有时，尤其是在变量数量很少的情况下，我们想在图上添加变量标签。

我们首先生成带有10个变量的一些数据，然后，我们拟合glmnet模型，并绘制标准图。

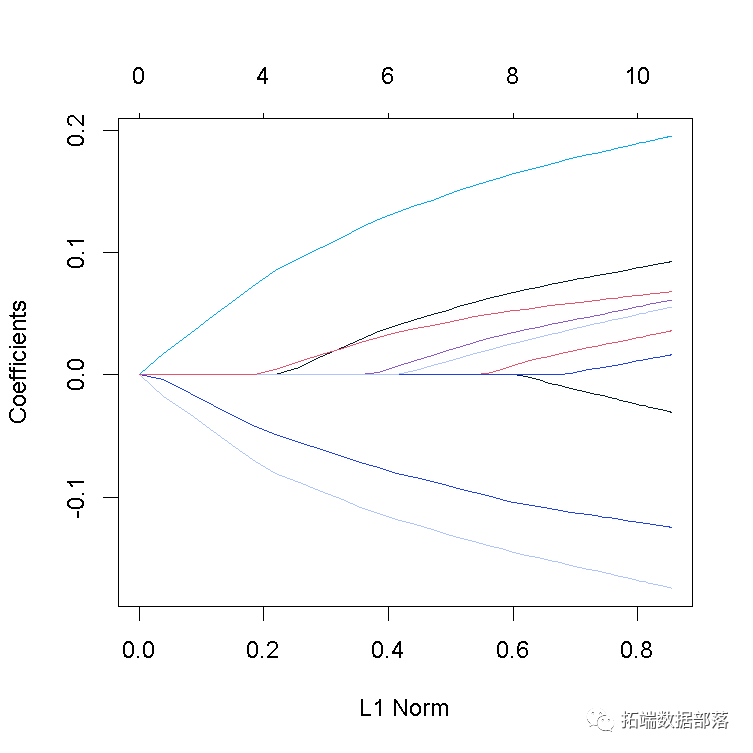
我们希望用变量名标记曲线。在路径的末尾放置系数的位置。

多元正态

使用family = "mgaussian" option 获得多元正态分布glmnet。

显然，顾名思义，y不是向量，而是矩阵。结果，每个λ值的系数也是一个矩阵。

在这里，我们解决以下问题：

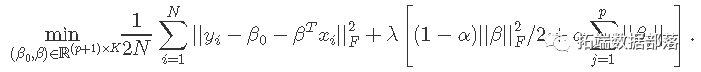
这里，βj是p×K系数矩阵β的第j行，对于单个预测变量xj，我们用每个系数K向量βj的组套索罚分代替每个单一系数的绝对罚分。

我们使用预先生成的一组数据进行说明。

我们拟合数据，并返回对象“ mfit”。

mfit = glmnet(x, y, family = "mgaussian")

如果为 standardize.response = TRUE，则将因变量标准化。

为了可视化系数，我们使用 plot 函数。

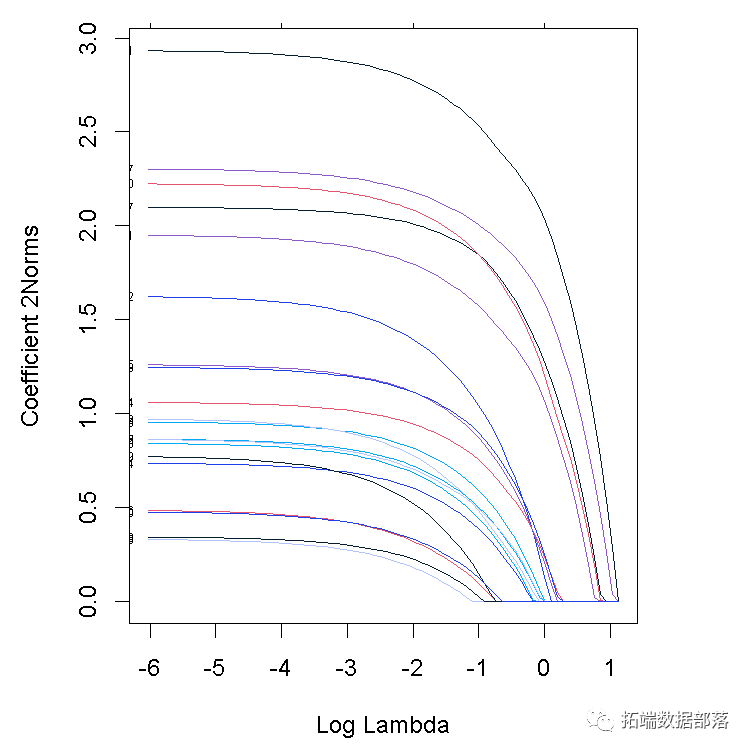
注意我们设置了 type.coef = "2norm"。在此设置下，每个变量绘制一条曲线，其值等于ℓ2范数。默认设置为 type.coef = "coef"，其中为每个因变量创建一个系数图。

通过使用该函数coef ，我们可以提取要求的λ值的系数， 并通过进行预测 。

## , , 1
## 
##           y1      y2      y3    y4
## \[1,\] -4.7106 -1.1635  0.6028 3.741
## \[2,\]  4.1302 -3.0508 -1.2123 4.970
## \[3,\]  3.1595 -0.5760  0.2608 2.054
## \[4,\]  0.6459  2.1206 -0.2252 3.146
## \[5,\] -1.1792  0.1056 -7.3353 3.248
## 
## , , 2
## 
##           y1      y2      y3    y4
## \[1,\] -4.6415 -1.2290  0.6118 3.780
## \[2,\]  4.4713 -3.2530 -1.2573 5.266
## \[3,\]  3.4735 -0.6929  0.4684 2.056
## \[4,\]  0.7353  2.2965 -0.2190 2.989
## \[5,\] -1.2760  0.2893 -7.8259 3.205

预测结果保存在三维数组中，其中前两个维是每个因变量的预测矩阵，第三个维表示因变量。

我们还可以进行k折交叉验证。

我们绘制结果 cv.glmnet 对象“ cvmfit”。

显示选定的λ最佳值

cvmfit$lambda.min

## \[1\] 0.04732

cvmfit$lambda.1se

## \[1\] 0.1317

逻辑回归

当因变量是分类的时，逻辑回归是另一个广泛使用的模型。如果有两个可能的结果，则使用二项式分布，否则使用多项式。

二项式模型

对于二项式模型，假设因变量的取值为G = {1,2} 。表示yi = I（gi = 1）。我们建模

可以用以下形式写

惩罚逻辑回归的目标函数使用负二项式对数似然

我们的算法使用对数似然的二次逼近，然后对所得的惩罚加权最小二乘问题进行下降。这些构成了内部和外部循环。

出于说明目的，我们 从数据文件加载预生成的输入矩阵 x 和因变量 y。

对于二项式逻辑回归，因变量y可以是两个级别的因子，也可以是计数或比例的两列矩阵。

glmnet 二项式回归的其他可选参数与正态分布的参数 几乎相同。不要忘记将family 选项设置 为“ binomial”。

fit = glmnet(x, y, family = "binomial")

像以前一样，我们可以输出和绘制拟合的对象，提取特定λ处的系数，并进行预测。

逻辑回归略有不同，主要体现在选择上 type。“链接”和“因变量”不等价，“类”仅可用于逻辑回归。总之，*“链接”给出了线性预测变量

• “因变量”给出合适的概率

• “类别”产生对应于最大概率的类别标签。

• “系数”计算值为的系数 s

在下面的示例中，我们在λ=0.05,0.01的情况下对类别标签进行了预测。

##      1   2  
## \[1,\] "0" "0"
## \[2,\] "1" "1"
## \[3,\] "1" "1"
## \[4,\] "0" "0"
## \[5,\] "1" "1"

对于逻辑回归，type.measure：

• “偏差”使用实际偏差。

• “ mae”使用平均绝对误差。

• “class”给出错误分类错误。

• “ auc”（仅适用于两类逻辑回归）给出了ROC曲线下的面积。

例如，

它使用分类误差作为10倍交叉验证的标准。

我们绘制对象并显示λ的最佳值。

cvfit$lambda.min

## \[1\] 0.01476

cvfit$lambda.1se

## \[1\] 0.02579

coef 并且 predict 类似于正态分布案例，因此我们省略了细节。我们通过一些例子进行回顾。

## 31 x 1 sparse Matrix of class "dgCMatrix"
##                    1
## (Intercept)  0.24371
## V1           0.06897
## V2           0.66252
## V3          -0.54275
## V4          -1.13693
## V5          -0.19143
## V6          -0.95852
## V7           .      
## V8          -0.56529
## V9           0.77454
## V10         -1.45079
## V11         -0.04363
## V12         -0.06894
## V13          .      
## V14          .      
## V15          .      
## V16          0.36685
## V17          .      
## V18         -0.04014
## V19          .      
## V20          .      
## V21          .      
## V22          0.20882
## V23          0.34014
## V24          .      
## V25          0.66310
## V26         -0.33696
## V27         -0.10570
## V28          0.24318
## V29         -0.22445
## V30          0.11091

如前所述，此处返回的结果仅针对因子因变量的第二类。

##       1  
##  \[1,\] "0"
##  \[2,\] "1"
##  \[3,\] "1"
##  \[4,\] "0"
##  \[5,\] "1"
##  \[6,\] "0"
##  \[7,\] "0"
##  \[8,\] "0"
##  \[9,\] "1"
## \[10,\] "1"

多项式模型

对于多项式模型，假设因变量变量的K级别为G = {1,2，…，K}。在这里我们建模

设Y为N×K指标因变量矩阵，元素yiℓ= I（gi =ℓ）。然后弹性网惩罚的负对数似然函数变为

β是系数的p×K矩阵。βk指第k列（对于结果类别k），βj指第j行（变量j的K个系数的向量）。最后一个惩罚项是||βj|| q ，我们对q有两个选择：q∈{1,2}。当q = 1时，这是每个参数的套索惩罚。当q = 2时，这是对特定变量的所有K个系数的分组套索惩罚，这使它们在一起全为零或非零。

对于多项式情况，用法类似于逻辑回归，我们加载一组生成的数据。

glmnet 除少数情况外，多项式逻辑回归中的可选参数 与二项式回归基本相似。

多项式回归的一个特殊选项是 type.multinomial，如果允许，则允许使用分组的套索罚分 type.multinomial = "grouped"。这将确保变量的多项式系数全部一起输入或输出，就像多元因变量一样。

我们绘制结果。

我们还可以进行交叉验证并绘制返回的对象。

预测最佳选择的λ：

##       1  
##  \[1,\] "3"
##  \[2,\] "2"
##  \[3,\] "2"
##  \[4,\] "1"
##  \[5,\] "1"
##  \[6,\] "3"
##  \[7,\] "3"
##  \[8,\] "1"
##  \[9,\] "1"
## \[10,\] "2"

泊松模型

Poisson回归用于在假设Poisson误差的情况下对计数数据进行建模，或者在均值和方差成比例的情况下使用非负数据进行建模。泊松也是指数分布族的成员。我们通常以对数建模：。
给定观测值的对数似然

和以前一样，我们优化了惩罚对数：

Glmnet使用外部牛顿循环和内部加权最小二乘循环（如逻辑回归）来优化此标准。

首先，我们加载一组泊松数据。

再次，绘制系数。

像以前一样，我们可以 分别使用coef 和 提取系数并在特定的λ处进行预测 predict。

例如，我们可以

## 21 x 1 sparse Matrix of class "dgCMatrix"
##                    1
## (Intercept)  0.61123
## V1           0.45820
## V2          -0.77061
## V3           1.34015
## V4           0.04350
## V5          -0.20326
## V6           .      
## V7           .      
## V8           .      
## V9           .      
## V10          .      
## V11          .      
## V12          0.01816
## V13          .      
## V14          .      
## V15          .      
## V16          .      
## V17          .      
## V18          .      
## V19          .      
## V20          .

##            1       2
## \[1,\]  2.4944  4.4263
## \[2,\] 10.3513 11.0586
## \[3,\]  0.1180  0.1782
## \[4,\]  0.9713  1.6829
## \[5,\]  1.1133  1.9935

我们还可以使用交叉验证来找到最佳的λ，从而进行推断。

选项几乎与正态族相同，不同之处在于 type.measure，“ mse”代表均方误差，“ mae”代表均值绝对误差。

我们可以绘制 cv.glmnet 对象。

我们还可以显示最佳的λ和相应的系数。

## 21 x 2 sparse Matrix of class "dgCMatrix"
##                     1        2
## (Intercept)  0.031263  0.18570
## V1           0.619053  0.57537
## V2          -0.984550 -0.93212
## V3           1.525234  1.47057
## V4           0.231591  0.19692
## V5          -0.336659 -0.30469
## V6           0.001026  .      
## V7          -0.012830  .      
## V8           .         .      
## V9           .         .      
## V10          0.015983  .      
## V11          .         .      
## V12          0.030867  0.02585
## V13         -0.027971  .      
## V14          0.032750  .      
## V15         -0.005933  .      
## V16          0.017506  .      
## V17          .         .      
## V18          0.004026  .      
## V19         -0.033579  .      
## V20          0.012049  0.00993

Cox模型

Cox比例风险模型通常用于研究预测变量与生存时间之间的关系。

Cox比例风险回归模型，它不是直接考察 与X的关系，而是用 作为因变量，模型的基本形式为：

式中， 为自变量的偏回归系数，它是须从样本数据作出估计的参数； 是当X向量为0时， 的基准危险率，它是有待于从样本数据作出估计的量。简称为Cox回归模型。

由于Cox回归模型对 未作任何假定，因此Cox回归模型在处理问题时具有较大的灵活性；另一方面，在许多情况下，我们只需估计出参数 (如因素分析等)，即使在 未知的情况下，仍可估计出参数 。这就是说，Cox回归模型由于含有 ，因此它不是完全的参数模型，但仍可根据公式(1)作出参数 的估计，故Cox回归模型属于半参数模型。

公式可以转化为：

我们使用一组预先生成的样本数据。用户可以加载自己的数据并遵循类似的过程。在这种情况下，x必须是协变量值的n×p矩阵-每行对应一个患者，每列对应一个协变量。y是一个n×2矩阵。

##         time status
## \[1,\] 1.76878      1
## \[2,\] 0.54528      1
## \[3,\] 0.04486      0
## \[4,\] 0.85032      0
## \[5,\] 0.61488      1

Surv 包中的 函数 survival 可以创建这样的矩阵。

我们计算默认设置下的求解路径。

绘制系数。

提取特定值λ处的系数。

## 30 x 1 sparse Matrix of class "dgCMatrix"
##            1
## V1   0.37694
## V2  -0.09548
## V3  -0.13596
## V4   0.09814
## V5  -0.11438
## V6  -0.38899
## V7   0.24291
## V8   0.03648
## V9   0.34740
## V10  0.03865
## V11  .      
## V12  .      
## V13  .      
## V14  .      
## V15  .      
## V16  .      
## V17  .      
## V18  .      
## V19  .      
## V20  .      
## V21  .      
## V22  .      
## V23  .      
## V24  .      
## V25  .      
## V26  .      
## V27  .      
## V28  .      
## V29  .      
## V30  .

函数 cv.glmnet 可用于计算Cox模型的k折交叉验证。

拟合后，我们可以查看最佳λ值和交叉验证的误差图，帮助评估我们的模型。

如前所述，图中的左垂直线向我们显示了CV误差曲线达到最小值的位置。右边的垂直线向我们展示了正则化的模型，其CV误差在最小值的1个标准偏差之内。我们还提取了最优λ。

cvfit$lambda.min

## \[1\] 0.01594

cvfit$lambda.1se

## \[1\] 0.04869

我们可以检查模型中的协变量并查看其系数。

index.min

##  \[1\]  0.491297 -0.174601 -0.218649  0.175112 -0.186673 -0.490250  0.335197
##  \[8\]  0.091587  0.450169  0.115922  0.017595 -0.018365 -0.002806 -0.001423
## \[15\] -0.023429  0.001688 -0.008236

coef.min

## 30 x 1 sparse Matrix of class "dgCMatrix"
##             1
## V1   0.491297
## V2  -0.174601
## V3  -0.218649
## V4   0.175112
## V5  -0.186673
## V6  -0.490250
## V7   0.335197
## V8   0.091587
## V9   0.450169
## V10  0.115922
## V11  .       
## V12  .       
## V13  0.017595
## V14  .       
## V15  .       
## V16  .       
## V17 -0.018365
## V18  .       
## V19  .       
## V20  .       
## V21 -0.002806
## V22 -0.001423
## V23  .       
## V24  .       
## V25 -0.023429
## V26  .       
## V27  0.001688
## V28  .       
## V29  .       
## V30 -0.008236

稀疏矩阵

我们的程序包支持稀疏的输入矩阵，该矩阵可以高效地存储和操作大型矩阵，但只有少数几个非零条目。

我们加载一组预先创建的样本数据。

加载100 * 20的稀疏矩阵和 y因向量。

## \[1\] "dgCMatrix"
## attr(,"package")
## \[1\] "Matrix"

我们可以像以前一样拟合模型。

fit = glmnet(x, y)

进行交叉验证并绘制结果对象。

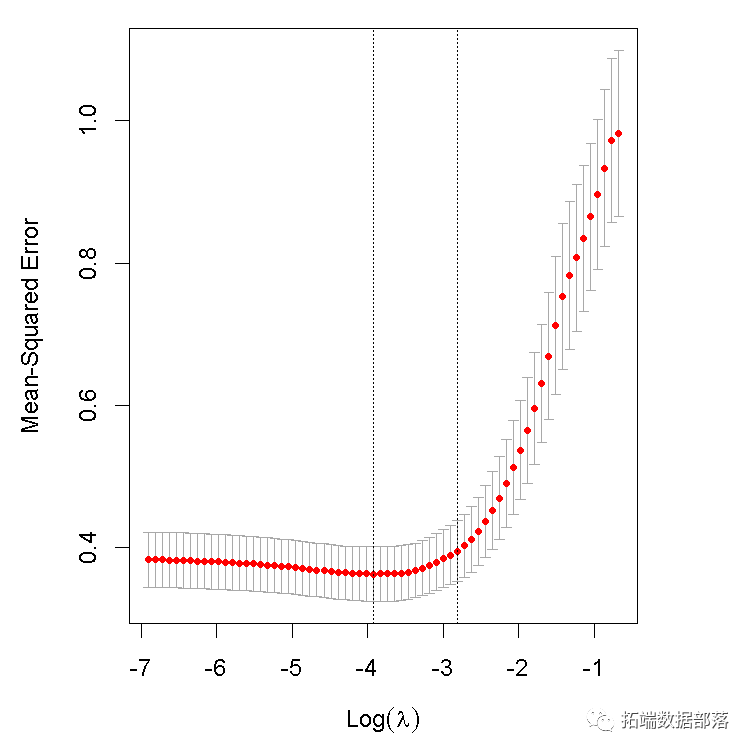
预测新输入矩阵 。例如，

##            1
## \[1,\]  0.3826
## \[2,\] -0.2172
## \[3,\] -1.6622
## \[4,\] -0.4175
## \[5,\] -1.3941

参考文献

Jerome Friedman, Trevor Hastie and Rob Tibshirani. (2008).
Regularization Paths for Generalized Linear Models via Coordinate Descent