我家自动化

这个屌丝很懒，什么也没留下！

热门标签

算法刷题记录1_对一数组进行逐步累加求和,prefix代表从前向后累加值, suffix代表从后向前累加值,

作者：我家自动化 | 2024-02-06 16:26:42

踩

对一数组进行逐步累加求和,prefix代表从前向后累加值, suffix代表从后向前累加值,

第一题CSP202112-1题

description

解题思路

$令N = A_n + 1 ，则有：$

$0=A_0<A_1 <⋅⋅⋅<A_i<⋅⋅⋅<A_n <A~n+1 =N$

$A_i\le x<A_{i+1},0\le i\le nA i ≤x<A i+1 ,0≤i≤n，有f ( x ) = i f(x)=if(x)=i。则：$

$s u m (A) = i = 0 \sum n ((A i + 1 - A i ) * i)$

$$
sum(A)

i
∑

((A
i+1
−A
i
)∗i)
=(A
1
−A
0
)∗0+(A
2
−A
1
)∗2+(A
3
−A
2
)∗2+(A
4
−A
3
)∗3
=(2−0)∗0+(5−2)∗1+(8−5)∗2+(10−8)∗3
=15
$$

#include <iostream>
#include <vector>
using namespace std;

int main()
{
    int n,N;
    cin>>n>>N;
    vector <int> A;
    A.push_back(0);
    for(int i = 1;i <= n;i++){
        int Ai;
        cin>>Ai;
        A.push_back(Ai);
    }
    A.push_back(N);
    int sum = 0;
    for(int i = 0;i <= n;i++){
        sum += (A[i+1]-A[i])*i;
    }
    cout<<sum;
    return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

第二题CSP20219-1题

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-qLN7k3TA-1666588088085)(https://zxxtypora.oss-cn-shenzhen.aliyuncs.com/img/`5E~~2H$7~FCL}C]TS}M4RD.png)]

解题思路

分别计算max和min，min只需对重复的数字加一次即可

#include <iostream>
#include <vector>
using namespace std;

int main()
{
    int n;
    cin>>n;
    vector <int> B;
    for(int i = 0;i < n;i++){
        int Bi;
        cin>>Bi;
        B.push_back(Bi);
    }
    int max = 0;
    for(int i = 0;i < n;i++){
        max += B[i];
    }
    cout<<max<<endl;
    int min = 0;
    int last = 0;
    for(int i = 0;i < n;i++){
        if(last != B[i]){
            min += B[i];
        }
            last = B[i];
    }
    cout<<min;
    return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

第三题力扣第二题

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-YGuR50Ad-1666588088086)(https://zxxtypora.oss-cn-shenzhen.aliyuncs.com/img/QQ图片20220309184524.png)]

解题

输入的两个链表都是逆序存储数字的位数的，因此两个链表中同一位置的数字可以直接相加。

同时遍历两个链表，逐位计算它们的和，并与当前位置的进位值相加。

class Solution {
public:
    ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
        ListNode *Head = NULL,*Last = NULL;
        int more = 0;
        while(l1||l2){
            int n1 = l1 ? l1->val : 0;
            int n2 = l2 ? l2->val : 0;
            int sum = n1+n2+more;
            int result = sum%10;
            if(!Head){
                Head = Last = new ListNode(result);
            }else{
                Last->next = new ListNode(result);
                Last = Last->next;
            }
            if(l1)
                l1 = l1->next;
            if(l2)
                l2 = l2->next;
            more = sum/10;
        }
        if(more > 0){
            Last->next = new ListNode(more);
        }
        return Head;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

第四题力扣第三题

前提：滑动窗口及哈希表

使用一种数据结构来判断 是否有重复的字符，常用的数据结构为哈希集合（即 C++ 中的 std::unordered_set，Java 中的 HashSet

unordered_set提供了几个函数让我们可以增删查：

unordered_set::insert{

	是C++ STL中的内置函数，用于在unordered_set容器中插入新的{element}。仅当每个元素与容器中已经存在的任何其他元素不相等时才插入每个元素(unordered_set中的元素具有唯一值)。插入会根据容器的标准自动在该位置进行。这通过插入的元素数量有效地增加了容器的大小。

}
1
2
3
4
5

unordered_set::find{

	调用 unordered_set 的 find() 会返回一个迭代器。这个迭代器指向和参数哈希值匹配的元素，如果没有匹配的元素，会返回这个容器的结束迭代器
	
//count函数只会返回1,0
//对于count(x)
//若us中存在x,返回1，反之，返回0
}
1
2
3
4
5
6
7
8

unordered_set::erase

	erase() 迭代器的参数必须是一个指向容器中元素的、有效的、可解引用的迭代器，因此需要确保它不是容器的结束迭代器。这个版本的 erase() 函数会返回一个指向被删除元素的下一个位置的迭代器，如果删除的是最后一个元素，那么它就是结束迭代器。

}
1
2
3
4
5

这个unorder暗示着，这两个头文件中类的底层实现----Hash。也是因为如此，你才可以在声明这些unordered模版类的时候，传入一个自定义的哈希函数，准确的说是哈希函数子（hash function object）。

另外，实现 unordered_set 容器的模板类定义在<unordered_set>头文件，并位于 std 命名空间中。这意味着，如果程序中需要使用该类型容器，则首先应该包含如下代码：

#include <unordered_set>

template < class Key,            //容器中存储元素的类型
           class Hash = hash<Key>,    //确定元素存储位置所用的哈希函数
           class Pred = equal_to<Key>,   //判断各个元素是否相等所用的函数
           class Alloc = allocator<Key>   //指定分配器对象的类型
           > class unordered_set;
1
2
3
4
5

这道题主要用到思路是：滑动窗口

一个队列,比如例题中的 abcabcbb，进入这个队列（窗口）为 abc 满足题目要求，当再进入 a，队列变成了 abca，这时候不满足要求。所以，我们要移动这个队列！

如何移动？

我们只要把队列的左边的元素移出就行了，直到满足题目要求。

题目

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-nQXO6Yok-1666588088086)(https://zxxtypora.oss-cn-shenzhen.aliyuncs.com/img/QQ图片20220309202116.png)]

解题：

使用两个指针表示字符串中的某个子串（或窗口）的左右边界，其中左指针代表着上文中「枚举子串的起始位置」

在每一步的操作中，将左指针向右移动一格，表示开始枚举下一个字符作为起始位置，然后可以不断地向右移动右指针，但需要保证这两个指针对应的子串中没有重复的字符。

在移动结束后，这个子串就对应着以左指针开始的，不包含重复字符的最长子串。我录下这个子串的长度；

在枚举结束后，找到的最长的子串的长度即为答案。

#include <algorithm>
#include <math.h>
class Solution {
public:
    int lengthOfLongestSubstring(string s) {
        unordered_set<char> hash;
        int left = 0;//左指针
        int n = s.size();
        int maxNumber = 0;
        for(int i = 0;i < n;i++){//n隐含为右指针，一次循环右移一次
            while(hash.find(s[i]) != hash.end()){
                //查找值为key的元素，如果找到，则返回一个指向该元素的正向迭代器；如果没找到，				则返回一个与end()方法相同的迭代器
                hash.erase(s[left]);
                left++;
                //这段代码结果是不断从左缩小窗口，直到窗口中不存在与下一个字符重复的字符。
            }
            hash.insert(s[i]);//插入，真正的右指针移动
            maxNumber = max(maxNumber,i-left+1);
        }
        return maxNumber;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

java解法参考：

class Solution {
    public int lengthOfLongestSubstring(String s) {
        // 哈希集合，记录每个字符是否出现过
        Set<Character> occ = new HashSet<Character>();
        int n = s.length();
        // 右指针，初始值为 -1，相当于我们在字符串的左边界的左侧，还没有开始移动
        int rk = -1, ans = 0;
        for (int i = 0; i < n; ++i) {
            if (i != 0) {
                // 左指针向右移动一格，移除一个字符
                occ.remove(s.charAt(i - 1));
            }
            while (rk + 1 < n && !occ.contains(s.charAt(rk + 1))) {
                // 不断地移动右指针
                occ.add(s.charAt(rk + 1));
                ++rk;
            }
            // 第 i 到 rk 个字符是一个极长的无重复字符子串
            ans = Math.max(ans, rk - i + 1);
        }
        return ans;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

第五题

1.⼀维数组中的前缀和力扣303题

前缀和技巧适⽤于快速、频繁地计算⼀个索引区间内的元素之和。⼀维数组中的前缀和

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-yxsZJHd6-1666588088086)(https://zxxtypora.oss-cn-shenzhen.aliyuncs.com/img/QQ图片20220310194431.png)]

无前缀和方法

class NumArray {
 	private int[] nums;
 	public NumArray(int[] nums) {
 		this.nums = nums;
 	}
 
 	public int sumRange(int left, int right) {
 		int res = 0;
 		for (int i = left; i <= right; i++) {
 			res += nums[i];
 		}
	 return res;
 	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14

这样，可以达到效果，但是效率很差，因为 sumRange ⽅法会被频繁调⽤，⽽它的时间复杂度是 O(N)，其中 N 代表 nums 数组的⻓度。

这道题的最优解法是使⽤前缀和技巧，将 sumRange 函数的时间复杂度降为 O(1)，说白了就是不要在 sumRange ⾥⾯⽤ for 循环

class NumArray {
    // 前缀和数组
    private int[] preSum;
 	/* 输入1个数组，构造前缀和 */
    public NumArray(int[] nums) {
    // preSum[0] = 0，便于计算累加和
        preSum = new int[nums.length + 1];
    // 计算 nums 的累加和
        for (int i = 1; i < preSum.length; i++) {
            preSum[i] = preSum[i - 1] + nums[i - 1];
        }
    }
    /* 查询闭区间 [left, right] 的累加和 */
    public int sumRange(int left, int right) {
        return preSum[right + 1] - preSum[left];
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

核⼼思路是我们 new ⼀个新的数组 preSum 出来，preSum[i] 记录 nums[0…i-1] 的累加和

如图 10 = 3 + 5 + 2

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-wktnnWBB-1666588088086)(https://zxxtypora.oss-cn-shenzhen.aliyuncs.com/img/QQ图片20220310200023.png)]

看这个 preSum 数组，如果我想求索引区间 [1, 4] 内的所有元素之和，就可以通过 preSum[5] - preSum[1] 得出。这样，sumRange 函数仅仅需要做⼀次减法运算，避免了每次进⾏ for 循环调⽤，最坏时间复杂度为常数 O(1)。

C++解法参考

class NumArray {
public:
    vector <int> preSum;
    NumArray(vector<int>& nums) {
        int n = nums.size();
        preSum.resize(n+1);
        for(int i = 0;i<n;i++){
            preSum[i+1] = preSum[i]+nums[i];
        }
    }
    int sumRange(int left, int right) {
        return preSum[right+1]-preSum[left];
    }
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

第六题

2.二维矩阵中的前缀和力扣304题

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-3LTI6Z3N-1666588088087)(https://zxxtypora.oss-cn-shenzhen.aliyuncs.com/img/QQ图片20220310204950.png)]

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-C0NYlkZr-1666588088087)(https://zxxtypora.oss-cn-shenzhen.aliyuncs.com/img/QQ图片20220310205118.png)]

按照题⽬要求，矩阵左上⻆为坐标原点 (0, 0)，那么 sumRegion([2,1,4,3]) 就是图中红⾊的⼦矩阵，你需要返回该⼦矩阵的元素和 8。

当然，你可以⽤⼀个嵌套 for 循环去遍历这个矩阵，但这样的话 sumRegion 函数的时间复杂度就⾼了，算法的格局就低了。做这道题更好的思路和⼀维数组中的前缀和是⾮常类似的，如下图

我们可以维护⼀个⼆维 preSum 数组，专⻔记录以原点为顶点的矩阵的元素之和，就可以⽤⼏次加减运算算出任何⼀个⼦矩阵的元素和：

class NumMatrix {
	// 定义：preSum[i][j] 记录 matrix 中⼦矩阵 [0, 0, i-1, j-1] 的元素和
 	private int[][] preSum;
 	public NumMatrix(int[][] matrix) {
 		int m = matrix.length, n = matrix[0].length;
 		if (m == 0 || n == 0) return;
 		// 构造前缀和矩阵
 		preSum = new int[m + 1][n + 1];
 		for (int i = 1; i <= m; i++) {
 			for (int j = 1; j <= n; j++) {
 			// 计算每个矩阵 [0, 0, i, j] 的元素和
 				preSum[i][j] = preSum[i-1][j] + preSum[i][j-1]
                    + matrix[i- 1][j - 1] - preSum[i-1][j-1];
			}
 		}
 	}
 		// 计算⼦矩阵 [x1, y1, x2, y2] 的元素和
 		public int sumRegion(int x1, int y1, int x2, int y2) {
 			// ⽬标矩阵之和由四个相邻矩阵运算获得
	 		return preSum[x2+1][y2+1] - preSum[x1][y2+1] 
            		- preSum[x2+1][y1] +preSum[x1][y1];
 		}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

第七题

3.和为k的子数组力扣560题

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-gjwT5iKQ-1666588088087)(https://zxxtypora.oss-cn-shenzhen.aliyuncs.com/img/QQ图片20220310214337.png)]

public class SumK {
	int subarraySum(int[] nums, int k) {
		//构造前缀和
		int n = nums.length;
		int [] preSum = new int [n + 1];
		preSum[0] = 0;
		//穷举子数组
		for (int i = 0; i < n; i++) {
			preSum[i+1] = preSum[i]+nums[i];
		}
		int res = 0;
        //穷举前缀数组中的元素和的差，等于目标数时res+1
		for (int i = 1; i <= n; i++) {
			for (int j = 0; j < i; j++) {
				//子数组nums元素[j...i-1]和
				if(preSum[i]-preSum[j] == k)
					res++;
			}
		}
		return res;
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

这个解法的时间复杂度 O(N^2) 空间复杂度 O(N)，并不是最优的解法。不过通过这个解法理解了前缀和数组的⼯作原理之后，可以使⽤⼀些巧妙的办法把时间复杂度进⼀步降低。

第⼆层 for 循环在⼲嘛呢？翻译⼀下就是，在计算，有⼏个 j 能够使得 presume[i] 和 presume[j] 的差为 k。毎找到⼀个这样的 j，就把结果加⼀。我们可以把 if 语句⾥的条件判断移项，这样写：

if (preSum[j] == preSum[i] - k)
    res++;
1
2

优化的思路是：直接记录下有⼏个 presume[j] 和 presume[i] - k 相等，直接更新结果，就避免了内层的 for 循环。我们可以⽤哈希表，在记录前缀和的同时记录该前缀和出现的次数。

int subarraySum(int[] nums, int k) {
 	int n = nums.length;
 	// map：前缀和 -> 该前缀和出现的次数
 	HashMap<Integer, Integer> 
	preSum = new HashMap<>();
 	// base case
 	preSum.put(0, 1);
 	int res = 0, sum0_i = 0;
 	for (int i = 0; i < n; i++) {
 		sum0_i += nums[i];
 		// 这是我们想找的前缀和 nums[0..j]
 		int sum0_j = sum0_i - k;
 		// 如果前⾯有这个前缀和，则直接更新答案
 		if (preSum.containsKey(sum0_j))
 		res += preSum.get(sum0_j);
 		// 把前缀和 nums[0..i] 加⼊并记录出现次数
 		preSum.put(sum0_i, 
			 preSum.getOrDefault(sum0_i, 0) + 1);
 	}
 	return res;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

C++解法参考

class Solution {
public:
    int subarraySum(vector<int>& nums, int k) {
        unordered_map<int, int> mp;
        mp[0] = 1;
        int count = 0, pre = 0;
        for (auto& x:nums) {
            pre += x;
            if (mp.find(pre - k) != mp.end()) {
                count += mp[pre - k];
            }
            mp[pre]++;
        }
        return count;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

JAVA 哈希图

HashMap 是一个散列表，它存储的内容是键值对(key-value)映射。

HashMap 实现了 Map 接口，根据键的 HashCode 值存储数据，具有很快的访问速度，最多允许一条记录的键为 null，不支持线程同步。

HashMap 是无序的，即不会记录插入的顺序。

HashMap 继承于AbstractMap，实现了 Map、Cloneable、java.io.Serializable 接口。

HashMap 的 key 与 value 类型可以相同也可以不同，可以是字符串（String）类型的 key 和 value，也可以是整型（Integer）的 key 和字符串（String）类型的 value。

基本类型	引用类型
boolean	Boolean
byte	Byte
short	Short
int	Integer
long	Long
float	Float
double	Double
char	Character

HashMap 类位于 java.util 包中，使用前需要引入它，语法格式如下：

import java.util.HashMap; // 引入 HashMap 类
1

添加键值对(key-value)可以使用 put() 方法:

可以使用 get(key) 方法来获取 key 对应的 value:

可以使用 remove(key) 方法来删除 key 对应的键值对(key-value):

所有键值对(key-value)可以使用 clear 方法：

计算 HashMap 中的元素数量可以使用 size() 方法：

使用 for-each 来迭代 HashMap 中的元素。

如果你只想获取 key，可以使用 keySet() 方法，然后可以通过 get(key) 获取对应的 value，如果你只想获取 value，可以使用 values() 方法。

Java HashMap 常用方法列表如下：

方法	描述
clear()	删除 hashMap 中的所有键/值对
clone()	复制一份 hashMap
isEmpty()	判断 hashMap 是否为空
size()	计算 hashMap 中键/值对的数量
put()	将键/值对添加到 hashMap 中
putAll()	将所有键/值对添加到 hashMap 中
putIfAbsent()	如果 hashMap 中不存在指定的键，则将指定的键/值对插入到 hashMap 中。
remove()	删除 hashMap 中指定键 key 的映射关系
containsKey()	检查 hashMap 中是否存在指定的 key 对应的映射关系。
containsValue()	检查 hashMap 中是否存在指定的 value 对应的映射关系。
replace()	替换 hashMap 中是指定的 key 对应的 value。
replaceAll()	将 hashMap 中的所有映射关系替换成给定的函数所执行的结果。
get()	获取指定 key 对应对 value
getOrDefault()	获取指定 key 对应对 value，如果找不到 key ，则返回设置的默认值
forEach()	对 hashMap 中的每个映射执行指定的操作。
entrySet()	返回 hashMap 中所有映射项的集合集合视图。
keySet()	返回 hashMap 中所有 key 组成的集合视图。
values()	返回 hashMap 中存在的所有 value 值。
merge()	添加键值对到 hashMap 中
compute()	对 hashMap 中指定 key 的值进行重新计算
computeIfAbsent()	对 hashMap 中指定 key 的值进行重新计算，如果不存在这个 key，则添加到 hashMap 中
computeIfPresent()	对 hashMap 中指定 key 的值进行重新计算，前提是该 key 存在于 hashMap 中。

第八题

差分数组

⽐如说，我给你输⼊⼀个数组 nums，然后⼜要求给区间 nums[2…6] 全部加 1，再给 nums[3…9] 全部减 3，再给 nums[0…4] 全部加 2，再给… ⼀通操作猛如⻁，然后问你，最后 nums 数组的值是什么？常规的思路很容易，你让我给区间 nums[i…j] 加上 val，那我就⼀个 for 循环给它们都加上呗，还能咋样？这种思路的时间复杂度是 O(N)，由于这个场景下对 nums 的修改⾮常频繁，所以效率会很低下。这⾥就需要差分数组的技巧，类似前缀和技巧构造的 prefix 数组，我们先对 nums 数组构造⼀个 diff 差分数组，diff[i] 就是 nums[i] 和 nums[i-1] 之差：

	int[] diff = new int[nums.length];
	// 构造差分数组
	diff[0] = nums[0];
	for (int i = 1; i < nums.length; i++) {
 		diff[i] = nums[i] - nums[i - 1];
	}

1
2
3
4
5
6
7

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-rbhfBR9h-1666588088087)(https://zxxtypora.oss-cn-shenzhen.aliyuncs.com/img/QQ图片20220312102944.png)]

通过这个 diff 差分数组是可以反推出原始数组 nums 的，代码逻辑如下：

	int[] res = new int[diff.length];
	// 根据差分数组构造结果数组
	res[0] = diff[0];
	for (int i = 1; i < diff.length; i++) {
		res[i] = res[i - 1] + diff[i];
	}
1
2
3
4
5
6

这样构造差分数组 diff，就可以快速进⾏区间增减的操作，如果你想对区间 nums[i…j] 的元素全部加 3，那么只需要让 diff[i] += 3，然后再让 diff[j+1] -= 3 即可

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-kVp9NCNi-1666588088088)(https://zxxtypora.oss-cn-shenzhen.aliyuncs.com/img/QQ图片20220312103555.png)]

回想 diff 数组反推 nums 数组的过程，diff[i] += 3 意味着给 nums[i…] 所有的元素都加了 3，然后 diff[j+1] -= 3 ⼜意味着对于 nums[j+1…] 所有元素再减 3，那综合起来，是不是就是对 nums[i…j] 中的所有元素都加 3 了？

反推nums数组需要注意：

	public void increment(int i, int j, int val) {
 		diff[i] += val;
 		if (j + 1 < diff.length) {
 		diff[j + 1] -= val;
 		}
	}
1
2
3
4
5
6

当 j+1 >= diff.length 时，说明是对 nums[i] 及以后的整个数组都进⾏修改，那么就不需要再给 diff 数组减 val 了。

题目：区间加法力扣370题

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-kgiHXoQj-1666588088088)(https://zxxtypora.oss-cn-shenzhen.aliyuncs.com/img/QQ图片20220312104749.png)]

// 差分数组工具类
class Difference {
    // 差分数组
    private int[] diff;
    
    /* 输入一个初始数组，区间操作将在这个数组上进行 */
    public Difference(int[] nums) {
        assert nums.length > 0;
        diff = new int[nums.length];
        // 根据初始数组构造差分数组
        diff[0] = nums[0];
        for (int i = 1; i < nums.length; i++) {
            diff[i] = nums[i] - nums[i - 1];
        }
    }
 
    /* 给闭区间 [i,j] 增加 val（可以是负数）*/
    public void increment(int i, int j, int val) {
        diff[i] += val;
        if (j + 1 < diff.length) {
            diff[j + 1] -= val;
        }
    }
 
    /* 返回结果数组 */
    public int[] result() {
        int[] res = new int[diff.length];
        // 根据差分数组构造结果数组
        res[0] = diff[0];
        for (int i = 1; i < diff.length; i++) {
            res[i] = res[i - 1] + diff[i];
        }
        return res;
    }
}
 
//直接利用上面的工具方法
int[] getModifiedArray(int length, int[][] updates) {
    // nums 初始化为全 0
    int[] nums = new int[length];
    // 构造差分解法
    Difference df = new Difference(nums);
    for (int[] update : updates) {
        int i = update[0];
        int j = update[1];
        int val = update[2];
        df.increment(i, j, val);
    }
    
    return df.result();
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51

C++解法：

class Solution {
public:
    vector<int> getModifiedArray(int length, vector<vector<int>>& updates) {
        vector<int> arr(length + 1, 0);
        for (auto &update : updates) {
            auto start = update[0], end = update[1], val = update[2];
            arr[start] += val;
            arr[end + 1] -= val;
        }
        arr.pop_back();
        partial_sum(arr.begin(), arr.end(), arr.begin());
        return arr;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14

第九题力扣1109题

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-EglRZnb4-1666588088088)(https://zxxtypora.oss-cn-shenzhen.aliyuncs.com/img/QQ图片20220312110143.png)]

题意翻译为：输⼊⼀个⻓度为 n 的数组 nums，其中所有元素都是 0。再给你输⼊⼀个 bookings，⾥⾯是若⼲三元组 (i,j,k)，每个三元组的含义就是要求你给 nums 数组的闭区间 [i-1,j-1] 中所有元素都加上 k。请你返回最后的 nums 数组是多少？

PS：因为题⽬说的 n 是从 1 开始计数的，⽽数组索引从 0 开始，所以对于输⼊的三元组 (i,j,k)，数组区间应该对应 [i-1,j-1]。

int[] corpFlightBookings(int[][] bookings, int n) {
 	// nums 初始化为全 0
 	int[] nums = new int[n];
 	// 构造差分解法
 	Difference df = new Difference(nums);
 	for (int[] booking : bookings) {
 		// 注意转成数组索引要减⼀
 		int i = booking[0] - 1;
 		int j = booking[1] - 1;
 		int val = booking[2];
 		// 对区间 nums[i..j] 增加 val
 		df.increment(i, j, val);
 	}
 	// 返回最终的结果数组
 	return df.result();
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

C++：

class Solution {
public:
    vector<int> corpFlightBookings(vector<vector<int>>& bookings, int n) {
    	vector <int> nums(n);
        for (auto& booking : bookings) {
        	//构造差分数组
            nums[booking[0] - 1] += booking[2];
            if (booking[1] < n) {
            	//当booing[1]处于小于数组长度时候继续构造差分数组减的部分
                nums[booking[1]] -= booking[2];
            }
        }
        for (int i = 1; i < n; i++) {
            //求结果
            nums[i] += nums[i - 1];
        }
        return nums;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

第十题力扣1094题

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-0VI0d2C2-1666588088088)(https://zxxtypora.oss-cn-shenzhen.aliyuncs.com/img/QQ图片20220312113918.png)]

比较取巧的方法，既然路程的总长已经给定了不超过1000，那么先初始化一个1001 的数组，在上车点和下车点分别加上/减去乘客人数。然后遍历整个数组计算乘客人数，超过capacity则返回false。 12ms;

实际为差分数组

class Solution {
public:
    bool carPooling(vector<vector<int>>& trips, int capacity) {
        vector<int> road(1001, 0);
        for(auto & t: trips){
            road[t[1]] += t[0];
            road[t[2]] -= t[0];
        }
        int count = 0;
        for(auto i: road){
            count += i;
            if(count > capacity) return false;
        }
        return true;
    }
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

其他解法参考：比较直观的一个方法，16ms。根据上车地点排序，然后用一个map记录下车地点和乘客人数；每次pick up 新乘客前，先drop off旧的乘客。

暂时只看得懂部分

/*暂时只看得懂部分*/
class Solution {
public:
    bool carPooling(vector<vector<int>>& trips, int capacity) {
        sort(trips.begin(), trips.end(),
            [&](const vector<int> & t1, const vector<int> & t2){
                return t1[1] < t2[1];
            });
        map<int, int> m; // {end => passengers};
        int passengers = 0;
        for(auto t: trips){
            for(auto it = m.begin(); it != m.end();){
                if(it->first <= t[1]){
                    passengers -= it->second;
                    m.erase(it++);
                }
                else{
                    break;
                }
            }
            // new passengers get on
            passengers += t[0];
            if (passengers > capacity){
                return false;
            }
            m[t[2]] += t[0];
        }

        return true;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

滑动窗口改进

算法框架参考：

/* 滑动窗⼝算法框架 */
void slidingWindow(string s, string t) {
 	unordered_map<char, int> need, window;
 	for (char c : t) need[c]++;
 	int left = 0, right = 0;
 	int valid = 0; 
 	while (right < s.size()) {
 		// c 是将移⼊窗⼝的字符
 		char c = s[right];
 		// 右移窗⼝
 		right++;
 		// 进⾏窗⼝内数据的⼀系列更新
 		...
 		/*** debug 输出的位置 ***/
 		printf("window: [%d, %d)\n", left, right);
 		/********************/
 
		 // 判断左侧窗⼝是否要收缩
 		while (window needs shrink) {
		 	// d 是将移出窗⼝的字符
 			char d = s[left];
 			// 左移窗⼝
 			left++;
 			// 进⾏窗⼝内数据的⼀系列更新
 			...
 		}
 	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

第十一题力扣76题

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-dTCZfJSm-1666588088088)(https://zxxtypora.oss-cn-shenzhen.aliyuncs.com/img/QQ图片20220312125113.png)]

暴力解法思路：

	for (int i = 0; i < s.size(); i++)
 		for (int j = i + 1; j < s.size(); j++)
 			if s[i:j] 包含 t 的所有字⺟:
 				更新答案
1
2
3
4

思路很直接，但是显然，这个算法的复杂度肯定⼤于 O(N^2) 了，不好。

滑动窗⼝算法的思路是这样：

1、我们在字符串 S 中使⽤双指针中的左右指针技巧，初始化 left = right = 0，把索引左闭右开区间 [left, right) 称为⼀个「窗⼝」。

2、我们先不断地增加 right 指针扩⼤窗⼝ [left, right)，直到窗⼝中的字符串符合要求（包含了 T 中的所有字符）。

3、此时，我们停⽌增加 right，转⽽不断增加 left 指针缩⼩窗⼝ [left, right)，直到窗⼝中的字符串不再符合要求（不包含 T 中的所有字符了）。同时，每次增加 left，我们都要更新⼀轮结果。

4、重复第 2 和第 3 步，直到 right 到达字符串 S 的尽头。这个思路其实也不难，第 2 步相当于在寻找⼀个「可⾏解」，然后第 3 步在优化这个「可⾏解」，最终找到最优解，也就是最短的覆盖⼦串。左右指针轮流前进，窗⼝⼤⼩增增减减，窗⼝不断向右滑动，这就是「滑动窗⼝」这个名字的来历。

下⾯画图理解⼀下，needs 和 window 相当于计数器，分别记录 T 中字符出现次数和「窗⼝」中的相应字符的出现次数。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-rwTknXZt-1666588088088)(https://zxxtypora.oss-cn-shenzhen.aliyuncs.com/img/QQ图片20220312125834.png)]

增加 right，直到窗⼝ [left, right] 包含了 T 中所有字符：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-D12U4NrS-1666588088089)(https://zxxtypora.oss-cn-shenzhen.aliyuncs.com/img/QQ图片20220312125923.png)]

现在开始增加 left，缩⼩窗⼝ [left, right]：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-pEpdhU1X-1666588088093)(https://zxxtypora.oss-cn-shenzhen.aliyuncs.com/img/QQ图片20220312130009.png)]

之后重复上述过程，先移动 right，再移动 left…… 直到 right 指针到达字符串 S 的末端，算法结束。

解题步骤

⾸先，初始化 window 和 need 两个哈希表，记录窗⼝中的字符和需要凑⻬的字符：

unordered_map<char, int> need, window;
for (char c : t) need[c]++;
1
2

然后，使⽤ left 和 right 变量初始化窗⼝的两端，不要忘了，区间 [left, right) 是左闭右开的，所以初始情况下窗⼝没有包含任何元素：

int left = 0, right = 0;
int valid = 0; 
while (right < s.size()) {
 	// 开始滑动
}
1
2
3
4
5

现在开始套模板，只需要思考以下四个问题：

1、当移动 right 扩⼤窗⼝，即加⼊字符时，应该更新哪些数据？

2、什么条件下，窗⼝应该暂停扩⼤，开始移动 left 缩⼩窗⼝？

3、当移动 left 缩⼩窗⼝，即移出字符时，应该更新哪些数据

4、我们要的结果应该在扩⼤窗⼝时还是缩⼩窗⼝时进⾏更新？

如果⼀个字符进⼊窗⼝，应该增加 window 计数器；

如果⼀个字符将移出窗⼝的时候，应该减少 window 计数器；

当 valid 满⾜ need 时应该收缩窗⼝；

应该在收缩窗⼝的时候更新最终结果。

string minWindow(string s, string t) {
    unordered_map<char,int> need, window;
    for (char c : t) need[c]++;
    int left = 0, right = 0;
    int valid = 0;
    // 记录最小覆盖串的起始索引及长度
    int start = 0, len = INT_MAX;//int最大值
    while (right < s.size()) {
        // c 是将移窗口的字符
        char c = s[right];
        // 右移窗口
        right++;
        // 窗口内数据的系列更新
        if (need.count(c)) {
            window[c]++;
            if(window[c] == need[c])
                valid++;
        }
        //判断左侧窗口是否收缩
        while (valid == need.size()) {
            //更新最小覆盖子串
            if(right - left < len){
                start = left;
                len = right - left;
            }
            //d是将移出窗口的字符
            char d = s[left];
            //左移窗口xx
            left++;
            //窗口内数据更新
            if(need.count(d)){
                if(window[d] == need[d])
                    valid--;
                window[d]--;
            }
        }
    }
    return len == INT_MAX ?
                "":s.substr(start,len);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

第十二题力扣567题

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-MAnx72Wf-1666588088094)(https://zxxtypora.oss-cn-shenzhen.aliyuncs.com/img/QQ图片20220312160302.png)]

注意，输⼊的 s1 是可以包含重复字符的，所以这个题难度不⼩。

这种题⽬，是明显的滑动窗⼝算法，相当给你⼀个 S 和⼀个 T，请问你 S 中是否存在⼀个⼦串，包含 T 中所有字符且不包含其他字符？

1、本题移动 left 缩⼩窗⼝的时机是窗⼝⼤于 t.size() 时，应为排列嘛，显然⻓度应该是⼀样的。

2、当发现 valid == need.size() 时，就说明窗⼝中就是⼀个合法的排列，所以⽴即返回 true。

bool checkInclusion(string t, string s) {
    unordered_map<char, int> need, window;
    for (char c : t) need[c]++;
    int left = 0, right = 0;
    int valid = 0;
    while (right < s.size()) {
        char c = s[right];
        right++;
        // 进行窗口内数据的一系列更新
        if (need.count(c)) {
            window[c]++;
            if (window[c] == need[c])
                valid++;
        }
        // 判断左侧窗口是否要收缩
        while (right - left >= t.size()) {
            // 在这里判断是否找到了合法的子串
            if (valid == need.size())
                return true;
            char d = s[left];
            left++;
            // 进行窗口内数据的一系列更新
            if (need.count(d)) {
                if (window[d] == need[d])
                    valid--;
                    window[d]--;
            }
        }
    }
    // 未找到符合条件的子串
    return false;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

第十三题力扣438题

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-IXL11p71-1666588088094)(https://zxxtypora.oss-cn-shenzhen.aliyuncs.com/img/QQ图片20220312163047.png)]

相当于，输⼊⼀个串 S，⼀个串 T，找到 S 中所有 T 的排列，返回它们的起始索引。直接默写⼀下框架，明确刚才讲的 4 个问题，即可秒杀这道题：

vector<int> findAnagrams(string s, string t) {
    unordered_map<char, int> need, window;
    for (char c : t) need[c]++;
    int left = 0, right = 0;
    int valid = 0;
    vector<int> res; // 记录结果
    while (right < s.size()) {
        char c = s[right];
        right++;
    // 进行窗口内数据的一系列更新
        if (need.count(c)) {
            window[c]++;
            if (window[c] == need[c])
                valid++;
        }
        // 判断左侧窗口是否要收缩
        while (right - left >= t.size()) {
        // 当窗口符合条件时，把起始索引加入 res
            if (valid == need.size())
                res.push_back(left);
            char d = s[left];
            left++;
        // 进行窗口内数据的一系列更新
            if (need.count(d)) {
                if (window[d] == need[d])
                    valid--;
            window[d]--;
            }
        }
    }
    return res;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

跟寻找字符串的排列⼀样，只是找到⼀个合法异位词（排列）之后将起始索引加⼊ res 即可。

上面力扣第三题改进代码

int lengthOfLongestSubstring(string s) {
 	unordered_map<char, int> window;
 	int left = 0, right = 0;
 	int res = 0; // 记录结果
 	while (right < s.size()) {
 		char c = s[right];
 		right++;
 		// 进⾏窗⼝内数据的⼀系列更新
 		window[c]++;
 		// 判断左侧窗⼝是否要收缩
 		while (window[c] > 1) {
 			char d = s[left];
 			left++;
 			// 进⾏窗⼝内数据的⼀系列更新
 			window[d]--;
 		}
 		// 在这⾥更新答案
 		res = max(res, right - left);
 	}
 	return res;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

是变简单了，连 need 和 valid 都不需要，⽽且更新窗⼝内数据也只需要简单的更新计数器 window 即可。

当 window[c] 值⼤于 1 时，说明窗⼝中存在重复字符，不符合条件，就该移动 left 缩⼩窗⼝了嘛。

唯⼀需要注意的是，在哪⾥更新结果 res 呢？我们要的是最⻓⽆重复⼦串，哪⼀个阶段可以保证窗⼝中的字符串是没有重复的呢？

这⾥和之前不⼀样，要在收缩窗⼝完成后更新 res，因为窗⼝收缩的 while 条件是存在重复元素，换句话说收缩完成后⼀定保证窗⼝中没有重复嘛。

二分查找

⼆分查找并不简单，Knuth ⼤佬（发明 KMP 算法的那位）都说⼆分查找：思路很简单，细节是魔⻤。很多⼈喜欢拿整型溢出的 bug 说事⼉，但是⼆分查找真正的坑根本就不是那个细节问题，⽽是在于到底要给 mid 加⼀还是减⼀，while ⾥到底⽤ <= 还是 <。你要是没有正确理解这些细节，写⼆分肯定就是⽞学编程，有没有 bug 只能靠菩萨保佑。

分析⼆分查找的⼀个技巧是：不要出现 else，⽽是把所有情况⽤ else if 写清楚，这样可以清楚地展现所有细节。本⽂都会使⽤ else if，旨在讲清楚，读者理解后可⾃⾏简化。

简单基本框架：

int binarySearch(int nums[], int target) {
    int left = 0, right = ...;
    while(...) {
        int mid = left + (right - left) / 2;
        if (nums[mid] == target) {
            ...
        } else if (nums[mid] < target) {
            left = ...
        } else if (nums[mid] > target) {
            right = ...
        }
    }
    return ...;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14

另外声明⼀下，计算 mid 时需要防⽌溢出：

代码中 left + (right - left) / 2 就和 (left + right) / 2 的结果相同，但是有效防⽌了 left 和 right 太⼤直接相加导致溢出。

其中 … 标记的部分，就是可能出现细节问题的地⽅，当你⻅到⼀个⼆分查找的代码时，⾸先注意这⼏个地⽅

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-lSQcmbF0-1666588088094)(https://zxxtypora.oss-cn-shenzhen.aliyuncs.com/img/QQ图片20220312172853.png)]

初始化 right 的赋值是 nums.length - 1，即最后⼀个元素的索引，⽽不是 nums.length。这⼆者可能出现在不同功能的⼆分查找中，区别是：前者相当于两端都闭区间 [left, right]，后者相当于左闭右开区间 [left, right)，因为索引⼤⼩为 nums.length 是越界的。我们这个算法中使⽤的是前者 [left, right] 两端都闭的区间。这个区间其实就是每次进⾏搜索的区间。

但如果没找到，就需要 while 循环终⽌，然后返回 -1。那 while 循环什么时候应该终⽌？搜索区间为空的时候应该终⽌，意味着你没得找了，就等于没找到

while(left <= right) 的终⽌条件是 left == right + 1，写成区间的形式就是 [right + 1, right]，或者带个具体的数字进去 [3, 2]，可⻅这时候区间为空，因为没有数字既⼤于等于 3 ⼜⼩于等于 2 的吧。所以这时候 while 循环终⽌是正确的，直接返回 -1 即可。

while(left < right) 的终⽌条件是 left == right，写成区间的形式就是 [right, right]，或者带个具体的数字进去 [2, 2]，这时候区间⾮空，还有⼀个数 2，但此时 while 循环终⽌了。也就是说这区间 [2, 2] 被漏掉了，索引 2 没有被搜索，如果这时候直接返回 -1 就是错误的。

最基本的⼆分查找算法：

因为我们初始化 right = nums.length - 1
所以决定了我们的「搜索区间」是 [left, right]
所以决定了 while (left <= right)
同时也决定了 left = mid+1 和 right = mid-1
因为我们只需找到⼀个 target 的索引即可
所以当 nums[mid] == target 时可以⽴即返回
1
2
3
4
5
6

第⼆个，寻找左侧边界的⼆分查找：

因为我们初始化 right = nums.length
所以决定了我们的「搜索区间」是 [left, right)
所以决定了 while (left < right)
同时也决定了 left = mid + 1 和 right = mid
因为我们需找到 target 的最左侧索引
所以当 nums[mid] == target 时不要⽴即返回
⽽要收紧右侧边界以锁定左侧边界
1
2
3
4
5
6
7

第三个，寻找右侧边界的⼆分查找：

因为我们初始化 right = nums.length
所以决定了我们的「搜索区间」是 [left, right)
所以决定了 while (left < right)
同时也决定了 left = mid + 1 和 right = mid
因为我们需找到 target 的最右侧索引
所以当 nums[mid] == target 时不要⽴即返回
⽽要收紧左侧边界以锁定右侧边界
⼜因为收紧左侧边界时必须 left = mid + 1
所以最后⽆论返回 left 还是 right，必须减⼀
1
2
3
4
5
6
7
8
9

⼆分搜索问题的泛化

什么问题可以运⽤⼆分搜索算法技巧？

⾸先，你要从题⽬中抽象出⼀个⾃变量 x，⼀个关于 x 的函数 f(x)，以及⼀个⽬标值 target。

同时，x, f(x), target 还要满⾜以下条件：

1、f(x) 必须是在 x 上的单调函数（单调增单调减都可以）。

2、题⽬是让你计算满⾜约束条件 f(x) == target 时的 x 的值。

// 函数 f 是关于⾃变量 x 的单调函数
int f(int x) {
 	// ...
}
// 主函数，在 f(x) == target 的约束下求 x 的最值
int solution(int[] nums, int target) {
 	if (nums.length == 0) return -1;
 	// 问⾃⼰：⾃变量 x 的最⼩值是多少？
 	int left = ...;
 	// 问⾃⼰：⾃变量 x 的最⼤值是多少？
 	int right = ... + 1;
 	while (left < right) {
 		int mid = left + (right - left) / 2;
 		if (f(mid) == target) {
 			// 问⾃⼰：题⽬是求左边界还是右边界？
 			// ...
 		} else if (f(mid) < target) {
 			// 问⾃⼰：怎么让 f(x) ⼤⼀点？
 			// ...
 		} else if (f(mid) > target) {
 			// 问⾃⼰：怎么让 f(x) ⼩⼀点？
 			// ...
 		}
 	}
 return left;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

具体来说，想要⽤⼆分搜索算法解决问题，分为以下⼏步：

1、确定 x, f(x), target 分别是什么，并写出函数 f 的代码。

2、找到 x 的取值范围作为⼆分搜索的搜索区间，初始化 left 和 right 变量。

3、根据题⽬的要求，确定应该使⽤搜索左侧还是搜索右侧的⼆分搜索算法，写出解法代码。

第十四题力扣875题

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-8tgzAvmU-1666588088094)(https://zxxtypora.oss-cn-shenzhen.aliyuncs.com/img/QQ图片20220312190142.png)]

那么，对于这道题，如何运用刚才总结的套路，写出二分搜索解法代码？

按步骤思考即可：

1、确定x, f(x), target分别是什么，并写出函数f的代码。

自变量x是什么呢？回忆之前的函数图像，二分搜索的本质就是在搜索自变量。

所以，题目让求什么，就把什么设为自变量，珂珂吃香蕉的速度就是自变量x。

那么，在x上单调的函数关系f(x)是什么？

显然，吃香蕉的速度越快，吃完所有香蕉堆所需的时间就越少，速度和时间就是一个单调函数关系。

所以，f(x)函数就可以这样定义：

若吃香蕉的速度为x根/小时，则需要f(x)小时吃完所有香蕉。

// 定义：速度为 x 时，需要 f(x) 小时吃完所有香蕉
// f(x) 随着 x 的增加单调递减
int f(int[] piles, int x) {
    int hours = 0;
    for (int i = 0; i < piles.length; i++) {
        hours += piles[i] / x;
        if (piles[i] % x > 0) {
            hours++;
        }
    }
    return hours;
}
1
2
3
4
5
6
7
8
9
10
11
12

target就很明显了，吃香蕉的时间限制H自然就是target，是对f(x)返回值的最大约束。

2、找到x的取值范围作为二分搜索的搜索区间，初始化left和right变量。

显然，最小速度应该是 1，最大速度是piles数组中元素的最大值，因为每小时最多吃一堆香蕉

这里可以有两种选择，要么你用一个 for 循环去遍历piles数组，计算最大值，要么你看题目给的约束，piles中的元素取值范围是多少，然后给right初始化一个取值范围之外的值。

我选择第二种，题目说了1 <= piles[i] <= 10^9，那么我就可以确定二分搜索的区间边界：

public int minEatingSpeed(int[] piles, int H) {
    int left = 1;
    // 注意，right 是开区间，所以再加一
    int right = 1000000000 + 1;

    // ...
}
1
2
3
4
5
6
7

3、根据题目的要求，确定应该使用搜索左侧还是搜索右侧的二分搜索算法，写出解法代码。

现在我们确定了自变量x是吃香蕉的速度，f(x)是单调递减的函数，target就是吃香蕉的时间限制H，题目要我们计算最小速度，也就是x要尽可能小：

这就是搜索左侧边界的二分搜索，不过注意f(x)是单调递减的，不要闭眼睛套框架，需要结合上图进行思考，写出代码：

public int minEatingSpeed(int[] piles, int H) {
    int left = 1;
    int right = 1000000000 + 1;
    while (left < right) {
        int mid = left + (right - left) / 2;
        if (f(piles, mid) == H) {
            // 搜索左侧边界，则需要收缩右侧边界
            right = mid;
        } else if (f(piles, mid) < H) {
            // 需要让 f(x) 的返回值大一些
            right = mid;
        } else if (f(piles, mid) > H) {
            // 需要让 f(x) 的返回值小一些
            left = mid + 1;
        }
    }
    return left;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

至此，这道题就解决了，现在可以把多余的 if 分支合并一下，最终代码如下：

public int minEatingSpeed(int[] piles, int H) {
    int left = 1;
    int right = 1000000000 + 1;

    while (left < right) {
        int mid = left + (right - left) / 2;
        if (f(piles, mid) <= H) {
            right = mid;
        } else {
            left = mid + 1;
        }
    }
    return left;
}

// 定义：速度为 x 时，需要 f(x) 小时吃完所有香蕉
// f(x) 随着 x 的增加单调递减
int f(int[] piles, int x) {
    int hours = 0;
    for (int i = 0; i < piles.length; i++) {
        hours += piles[i] / x;
        if (piles[i] % x > 0) {
            hours++;
        }
    }
    return hours;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

PS:代码框架中多余的 if 分支主要是帮助理解的，写出正确解法后建议合并多余的分支，可以提高算法运行的效率。

第十五题力扣1101题

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-YwvkCJZC-1666588088095)(https://zxxtypora.oss-cn-shenzhen.aliyuncs.com/img/QQ图片20220312194206.png)]

1、确定x, f(x), target分别是什么，并写出函数f的代码。

题目问什么，什么就是自变量，也就是说船的运载能力就是自变量x。

运输天数和运载能力成反比，所以可以让f(x)计算x的运载能力下需要的运输天数，那么f(x)是单调递减的。

函数f(x)的实现如下：

// 定义：当运载能力为 x 时，需要 f(x) 天运完所有货物
// f(x) 随着 x 的增加单调递减
int f(int[] weights, int x) {
    int days = 0;
    for (int i = 0; i < weights.length; ) {
        // 尽可能多装货物
        int cap = x;
        while (i < weights.length) {
            if (cap < weights[i]) break;
            else cap -= weights[i];
            i++;
        }
        days++;
    }
    return days;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

对于这道题，target显然就是运输天数D，我们要在f(x) == D的约束下，算出船的最小载重。

2、找到x的取值范围作为二分搜索的搜索区间，初始化left和right变量。

船的最小载重是多少？最大载重是多少？

显然，船的最小载重应该是weights数组中元素的最大值，因为每次至少得装一件货物走，不能说装不下嘛。

最大载重显然就是weights数组所有元素之和，也就是一次把所有货物都装走。

这样就确定了搜索区间[left, right)：

public int shipWithinDays(int[] weights, int days) {
    int left = 0;
    // 注意，right 是开区间，所以额外加一
    int right = 1;
    for (int w : weights) {
        left = Math.max(left, w);
        right += w;
    }

    // ...
}
1
2
3
4
5
6
7
8
9
10
11

3、需要根据题目的要求，确定应该使用搜索左侧还是搜索右侧的二分搜索算法，写出解法代码。

现在我们确定了自变量x是船的载重能力，f(x)是单调递减的函数，target就是运输总天数限制D，题目要我们计算船的最小载重，也就是x要尽可能小：

public int shipWithinDays(int[] weights, int days) {
    int left = 0;
    // 注意，right 是开区间，所以额外加一
    int right = 1;
    for (int w : weights) {
        left = Math.max(left, w);
        right += w;
    }

    while (left < right) {
        int mid = left + (right - left) / 2;
        if (f(weights, mid) == days) {
            // 搜索左侧边界，则需要收缩右侧边界
            right = mid;
        } else if (f(weights, mid) < days) {
            // 需要让 f(x) 的返回值大一些
            right = mid;
        } else if (f(weights, mid) > days) {
            // 需要让 f(x) 的返回值小一些
            left = mid + 1;
        }
    }
    
    return left;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

到这里，这道题的解法也写出来了，我们合并一下多余的 if 分支，提高代码运行速度，最终代码如下：

public int shipWithinDays(int[] weights, int days) {
    int left = 0;
    int right = 1;
    for (int w : weights) {
        left = Math.max(left, w);
        right += w;
    }

    while (left < right) {
        int mid = left + (right - left) / 2;
        if (f(weights, mid) <= days) {
            right = mid;
        } else {
            left = mid + 1;
        }
    }

    return left;
}

int f(int[] weights, int x) {
    int days = 0;
    for (int i = 0; i < weights.length; ) {
        // 尽可能多装货物
        int cap = x;
        while (i < weights.length) {
            if (cap < weights[i]) break;
            else cap -= weights[i];
            i++;
        }
        days++;
    }
    return days;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

原地修改数组

我们知道对于数组来说，在尾部插⼊、删除元素是⽐较⾼效的，时间复杂度是 O(1)，但是如果在中间或者开头插⼊、删除元素，就会涉及数据的搬移，时间复杂度为 O(N)，效率较低。

有序数组/链表去重力扣26题第十六题

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-xnLAl2Lq-1666588088095)(https://zxxtypora.oss-cn-shenzhen.aliyuncs.com/img/QQ图片20220313142338.png)]

显然，由于数组已经排序，所以重复的元素⼀定连在⼀起，找出它们并不难，但如果毎找到⼀个重复元素就⽴即删除它，就是在数组中间进⾏删除操作，整个时间复杂度是会达到 O(N^2)。

如果不是原地修改的话，我们直接 new ⼀个 int[] 数组，把去重之后的元素放进这个新数组中，然后返回这个新数组即可

但是原地删除，不允许我们 new 新数组，只能在原数组上操作，然后返回⼀个⻓度，这样就可以通过返回的⻓度和原始数组得到我们去重后的元素有哪些了。

这种需求在数组相关的算法题中时⾮常常⻅的，通⽤解法就是前⽂双指针技巧中的快慢指针技巧。

我们让慢指针 slow ⾛在后⾯，快指针 fast ⾛在前⾯探路，找到⼀个不重复的元素就告诉 slow 并让 slow 前进⼀步。这样当 fast 指针遍历完整个数组 nums 后，nums[0…slow] 就是不重复元素。

class Solution {
public:
    int removeDuplicates(vector<int>& nums) {
        if (nums.size() == 0){
            return 0;
        }
        int slow = 0, fast = 0;
        while(fast < nums.size()){
            if(nums[fast] != nums[slow]){
                slow++;
                nums[slow] = nums[fast];
            }
            fast++;
        }
        return slow+1;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

java写法参考：

int removeDuplicates(int[] nums) {
 	if (nums.length == 0) {
 		return 0;
 	}
 	int slow = 0, fast = 0;
 	while (fast < nums.length) {
 		if (nums[fast] != nums[slow]) {
 			slow++;
 			// 维护 nums[0..slow] ⽆重复
 			nums[slow] = nums[fast];
 		}
 		fast++;
 	}
 // 数组⻓度为索引 + 1
 return slow + 1;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

再简单扩展⼀下，如果给你⼀个有序链表，如何去重呢？！

第十七题力扣第 83 题

其实和数组去重是⼀模⼀样的，唯⼀的区别是把数组赋值操作变成操作指针⽽已

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ix7sMFre-1666588088096)(https://zxxtypora.oss-cn-shenzhen.aliyuncs.com/img/QQ图片20220313153819.png)]

class Solution {
public:
    ListNode* deleteDuplicates(ListNode* head) {
        if(head == NULL||head->next == NULL) return head;
        ListNode *slow = head; 
        ListNode *fast = head;
        while (fast != NULL){
            if(fast->val != slow->val){
                slow->next = fast;
                slow = slow->next;
            }
            fast = fast->next;
        }
        slow->next = NULL;
        return head;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

JAVA解法参考：

ListNode deleteDuplicates(ListNode head) {
 	if (head == null) return null;
 	ListNode slow = head, fast = head;
 	while (fast != null) {
 		if (fast.val != slow.val) {
 			// nums[slow] = nums[fast];
 			slow.next = fast;
 			// slow++;
 			slow = slow.next;
 		}
 		// fast++
 		fast = fast.next;
 	}
 	// 断开与后⾯重复元素的连接
 	slow.next = null;
 	return head;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

第十八题力扣第27题

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-pKHQdGEk-1666588088096)(https://zxxtypora.oss-cn-shenzhen.aliyuncs.com/img/QQ图片20220313154038.png)]

题⽬要求我们把 nums 中所有值为 val 的元素原地删除

依然需要使⽤双指针技巧中的快慢指针：如果 fast 遇到需要去除的元素，则直接跳过，否则就告诉 slow 指针，并让 slow 前进⼀步。这和前⾯说到的数组去重问题解法思路是完全⼀样的

class Solution {
public:
    int removeElement(vector<int>& nums, int val) {
        int fast = 0,slow = 0;
        while(fast < nums.size()){
            if(nums[fast] != val){
                nums[slow] = nums[fast];
                slow++;
            }
            fast++;
        }
        return slow;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14

java解法参考：

int removeElement(int[] nums, int val) {
 	int fast = 0, slow = 0;
 	while (fast < nums.length) {
 		if (nums[fast] != val) {
 			nums[slow] = nums[fast];
 			slow++;
 		}
 		fast++;
 	}
 	return slow;
}
1
2
3
4
5
6
7
8
9
10
11

第十九题力扣第283题

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-wm2Mpo6e-1666588088096)(https://zxxtypora.oss-cn-shenzhen.aliyuncs.com/img/QQ图片20220313160544.png)]

题⽬让我们将所有 0 移到最后，其实就相当于移除 nums 中的所有 0，然后再把后⾯的元素都赋值为 0 即可。

class Solution {
public:
    void moveZeroes(vector<int>& nums) {
        int fast = 0,slow = 0;
        while(fast < nums.size()){
            if(nums[fast] != 0){
                swap(nums[slow], nums[fast]);
                slow++;
            }
            fast++;
        }
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13

单链表及技巧

1、合并两个有序链表

2、合并 k 个有序链表

3、寻找单链表的倒数第 k 个节点

4、寻找单链表的中点

5、判断单链表是否包含环并找出环起点

6、判断两个单链表是否相交并找出交点

第二十题力扣21题

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-h3aPxk7P-1666588088096)(https://zxxtypora.oss-cn-shenzhen.aliyuncs.com/img/QQ图片20220315193242.png)]

class Solution {
public:
    ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
        ListNode* preHead = new ListNode(-1);
        ListNode* prev = preHead;
        while (l1 != nullptr && l2 != nullptr) {
            if (l1->val < l2->val) {
                prev->next = l1;
                l1 = l1->next;
            } else {
                prev->next = l2;
                l2 = l2->next;
            }
            prev = prev->next;
        }
        // 合并后 l1 和 l2 最多只有一个还未被合并完，我们直接将链表末尾指向未合并完的链表即可
        prev->next = l1 == nullptr ? l2 : l1;
        return preHead->next;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

JAVA参考:

ListNode mergeTwoLists(ListNode l1, ListNode l2) {
    // 虚拟头结点
    ListNode dummy = new ListNode(-1), p = dummy;
    ListNode p1 = l1, p2 = l2;
    while (p1 != null && p2 != null) {
        // 比较 p1 和 p2 两个指针
        // 将值较小的的节点接到 p 指针
        if (p1.val > p2.val) {
            p.next = p2;
            p2 = p2.next;
        } else {
            p.next = p1;
            p1 = p1.next;
        }
        // p 指针不断前进
        p = p.next;
    }
    if (p1 != null) {
        p.next = p1;
    }
    if (p2 != null) {
        p.next = p2;
    }
    return dummy.next;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

第二十一题力扣23题

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-NSlLOJiC-1666588088097)(https://zxxtypora.oss-cn-shenzhen.aliyuncs.com/img/QQ图片20220315195554.png)]

合并 k 个有序链表的逻辑类似合并两个有序链表，难点在于，如何快速得到 k 个节点中的最小节点，接到结果链表上？

这里我们就要用到优先级队列（二叉堆) 这种数据结构，把链表节点放入一个最小堆，就可以每次获得 k 个节点中的最小节点：

使用优先队列合并

我们需要维护当前每个链表没有被合并的元素的最前面一个，kk 个链表就最多有 kk 个满足这样条件的元素，每次在这些元素里面选取 val 属性最小的元素合并到答案中。在选取最小元素的时候，我们可以用优先队列来优化这个过程。

既然是队列那么先要包含头文件#include <queue>, 他和queue不同的就在于我们可以自定义其中数据的优先级让优先级高的排在队列前面,优先出队

优先队列具有队列的所有特性，包括基本操作，只是在这基础上添加了内部的一个排序，它本质是一个堆实现的

struct ListNode {
    int val;
    ListNode *next;
    ListNode() : val(0), next(nullptr) {}
    ListNode(int x) : val(x), next(nullptr) {}
    ListNode(int x, ListNode *next) : val(x), next(next) {}
};

class Solution {
public:
    struct Status {
        int val;
        ListNode *ptr;
        bool operator < (const Status &rhs) const {
            return val > rhs.val;
        }
    };

    priority_queue <Status> q;

    ListNode* mergeKLists(vector<ListNode*>& lists) {
        for (auto node: lists) {
            if (node) q.push({node->val, node});
        }
        ListNode head, *tail = &head;
        while (!q.empty()) {
            auto f = q.top(); q.pop();
            tail->next = f.ptr;
            tail = tail->next;
            if (f.ptr->next) q.push({f.ptr->next->val, f.ptr->next});
        }
        return head.next;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

这个算法是面试常考题，它的时间复杂度是多少呢？

优先队列 pq 中的元素个数最多是 k，所以一次 poll 或者 add 方法的时间复杂度是 O(logk)；所有的链表节点都会被加入和弹出 pq，所以算法整体的时间复杂度是 O(Nlogk)，其中 k 是链表的条数，N 是这些链表的节点总数。

单链表的倒数第 k 个节点

从前往后寻找单链表的第 k 个节点很简单，一个 for 循环遍历过去就找到了，但是如何寻找从后往前数的第 k 个节点呢？

那你可能说，假设链表有 n 个节点，倒数第 k 个节点就是正数第 n - k 个节点，不也是一个 for 循环的事儿吗？

是的，但是算法题一般只给你一个 ListNode 头结点代表一条单链表，你不能直接得出这条链表的长度 n，而需要先遍历一遍链表算出 n 的值，然后再遍历链表计算第 n - k 个节点。

也就是说，这个解法需要遍历两次链表才能得到出倒数第 k 个节点。

那么，我们能不能只遍历一次链表，就算出倒数第 k 个节点？可以做到的，如果是面试问到这道题，面试官肯定也是希望你给出只需遍历一次链表的解法。

这个解法就比较巧妙了，假设 k = 2，思路如下：

首先，我们先让一个指针 p1 指向链表的头节点 head，然后走 k 步：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-uIHz8mPR-1666588088097)(https://zxxtypora.oss-cn-shenzhen.aliyuncs.com/img/QQ图片20220315201526.png)]

现在的 p1，只要再走 n - k 步，就能走到链表末尾的空指针了对吧？

趁这个时候，再用一个指针 p2 指向链表头节点 head：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-d6rMPGyA-1666588088097)(https://zxxtypora.oss-cn-shenzhen.aliyuncs.com/img/QQ图片20220315201615.png)]

接下来就很显然了，让 p1 和 p2 同时向前走，p1 走到链表末尾的空指针时走了 n - k 步，p2 也走了 n - k 步，也就是链表的倒数第 k 个节点：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-pJrZ3Lk0-1666588088098)(https://zxxtypora.oss-cn-shenzhen.aliyuncs.com/img/QQ图片20220315201719.png)]

这样，只遍历了16一次链表，就获得了倒数第 k 个节点 p2。

// 返回链表的倒数第 k 个节点
ListNode findFromEnd(ListNode head, int k) {
    ListNode p1 = head;
    // p1 先走 k 步
    for (int i = 0; i < k; i++) {
        p1 = p1.next;
    }
    ListNode p2 = head;
    // p1 和 p2 同时走 n - k 步
    while (p1 != null) {
        p2 = p2.next;
        p1 = p1.next;
    }
    // p2 现在指向第 n - k 个节点
    return p2;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

无论遍历一次链表和遍历两次链表的时间复杂度都是 O(N)，但上述这个算法更有技巧性。

第二十三题力扣19题

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-gFM7YPfq-1666588088098)(https://zxxtypora.oss-cn-shenzhen.aliyuncs.com/img/QQ图片20220315202120.png)]

   ListNode* removeNthFromEnd(ListNode* head, int n) {
        ListNode* dummy = new ListNode(0, head);
        ListNode* first = head;
        ListNode* second = dummy;
        for (int i = 0; i < n; ++i) {
            first = first->next;
        }
        while (first) {//双快慢指针
            first = first->next;
            second = second->next;
        }
        second->next = second->next->next;
        ListNode* ans = dummy->next;
        delete dummy;//C++记得删除结点
        return ans;
   }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

这个逻辑就很简单了，要删除倒数第 n 个节点，就得获得倒数第 n + 1 个节点的引用，可以用我们实现的 findFromEnd 来操作。

不过注意我们又使用了虚拟头结点的技巧，也是为了防止出现空指针的情况，比如说链表总共有 5 个节点，题目就让你删除倒数第 5 个节点，也就是第一个节点，那按照算法逻辑，应该首先找到倒数第 6 个节点。但第一个节点前面已经没有节点了，这就会出错。

但有了我们虚拟节点 dummy 的存在，就避免了这个问题，能够对这种情况进行正确的删除。

单链表的中点

问题的关键也在于我们无法直接得到单链表的长度 n，常规方法也是先遍历链表计算 n，再遍历一次得到第 n / 2 个节点，也就是中间节点。

如果想一次遍历就得到中间节点，也需要耍点小聪明，使用「快慢指针」的技巧：

我们让两个指针 slow 和 fast 分别指向链表头结点 head。

每当慢指针 slow 前进一步，快指针 fast 就前进两步，这样，当 fast 走到链表末尾时，slow 就指向了链表中点。

第二十四题力扣876题

ListNode middleNode(ListNode head) {
    // 快慢指针初始化指向 head
    ListNode slow = head, fast = head;
    // 快指针走到末尾时停止
    while (fast != null && fast.next != null) {
        // 慢指针走一步，快指针走两步
        slow = slow.next;
        fast = fast.next.next;
    }
    // 慢指针指向中点
    return slow;
}
1
2
3
4
5
6
7
8
9
10
11
12

需要注意的是，如果链表长度为偶数，也就是说中点有两个的时候，我们这个解法返回的节点是靠后的那个节点。

另外，这段代码稍加修改就可以直接用到判断链表成环的算法题上。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-cXWkHsuK-1666588088098)(https://zxxtypora.oss-cn-shenzhen.aliyuncs.com/img/QQ图片20220315204221.png)]

class Solution {
public:
    ListNode* middleNode(ListNode* head) {
        ListNode *fast = head;ListNode *slow = head;
        while(fast&&fast->next){
            slow = slow->next;
            fast = fast->next->next;
        }
        return slow;
    }
};
1
2
3
4
5
6
7
8
9
10
11

方法二数组

class Solution {
public:
    ListNode* middleNode(ListNode* head) {
        vector<ListNode*> A = {head};
        while (A.back()->next != NULL)
            A.push_back(A.back()->next);
        return A[A.size() / 2];
    }
};
1
2
3
4
5
6
7
8
9

判断链表是否包含环

解决方案也是用快慢指针：

每当慢指针 slow 前进一步，快指针 fast 就前进两步。

如果 fast 最终遇到空指针，说明链表中没有环；如果 fast 最终和 slow 相遇，那肯定是 fast 超过了 slow 一圈，说明链表中含有环。

只需要把寻找链表中点的代码稍加修改就行了：

boolean hasCycle(ListNode head) {
    // 快慢指针初始化指向 head
    ListNode slow = head, fast = head;
    // 快指针走到末尾时停止
    while (fast != null && fast.next != null) {
        // 慢指针走一步，快指针走两步
        slow = slow.next;
        fast = fast.next.next;
        // 快慢指针相遇，说明含有环
        if (slow == fast) {
            return true;
        }
    }
    // 不包含环
    return false;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

这个问题还有进阶版：如果链表中含有环，如何计算这个环的起点？

ListNode detectCycle(ListNode head) {
    ListNode fast, slow;
    fast = slow = head;
    while (fast != null && fast.next != null) {
        fast = fast.next.next;
        slow = slow.next;
        if (fast == slow) break;
    }
    // 上面的代码类似 hasCycle 函数
    if (fast == null || fast.next == null) {
        // fast 遇到空指针说明没有环
        return null;
    }

    // 重新指向头结点
    slow = head;
    // 快慢指针同步前进，相交点就是环起点
    while (slow != fast) {
        fast = fast.next;
        slow = slow.next;
    }
    return slow;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

可以看到，当快慢指针相遇时，让其中任一个指针指向头节点，然后让它俩以相同速度前进，再次相遇时所在的节点位置就是环开始的位置。

只要我们把快慢指针中的任一个重新指向 head，然后两个指针同速前进，k - m 步后一定会相遇，相遇之处就是环的起点了。

两个链表是否相交

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-wg9PeLiK-1666588088099)(https://zxxtypora.oss-cn-shenzhen.aliyuncs.com/img/QQ图片20220316193712.png)][外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-UhSABA0a-1666588088099)(https://labuladong.gitee.io/algo/images/链表技巧/4.png)]

我们的算法应该返回 c1 这个节点。

这个题直接的想法可能是用 HashSet 记录一个链表的所有节点，然后和另一条链表对比，但这就需要额外的空间。

如果不用额外的空间，只使用两个指针，如何做呢？

难点在于，由于两条链表的长度可能不同，两条链表之间的节点无法对应

如果用两个指针 p1 和 p2 分别在两条链表上前进，并不能同时走到公共节点，也就无法得到相交节点 c1。

解决这个问题的关键是，通过某些方式，让 p1 和 p2 能够同时到达相交节点 c1。

所以，我们可以让 p1 遍历完链表 A 之后开始遍历链表 B，让 p2 遍历完链表 B 之后开始遍历链表 A，这样相当于「逻辑上」两条链表接在了一起。

如果这样进行拼接，就可以让 p1 和 p2 同时进入公共部分，也就是同时到达相交节点 c1：[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-mMlvDM8C-1666588088099)(https://zxxtypora.oss-cn-shenzhen.aliyuncs.com/img/{~J]4{R}I@UPZY]VTT{R]T1.png)]

如果说两个链表没有相交点，是否能够正确的返回 null 呢？

这个逻辑可以覆盖这种情况的，相当于 c1 节点是 null 空指针嘛，可以正确返回 null。

按照这个思路，可以写出如下代码：

ListNode getIntersectionNode(ListNode headA, ListNode headB) {
    // p1 指向 A 链表头结点，p2 指向 B 链表头结点
    ListNode p1 = headA, p2 = headB;
    while (p1 != p2) {
        // p1 走一步，如果走到 A 链表末尾，转到 B 链表
        if (p1 == null) p1 = headB;
        else            p1 = p1.next;
        // p2 走一步，如果走到 B 链表末尾，转到 A 链表
        if (p2 == null) p2 = headA;
        else            p2 = p2.next;
    }
    return p1;
}
1
2
3
4
5
6
7
8
9
10
11
12
13

class Solution {
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        ListNode *p1 = headA,*p2 = headB;
        while(p1 != p2){
            if(!p1)
                p1 = headB;
            else
                p1 = p1->next;
            if(!p2)
                p2 = headA;
            else
                p2 = p2->next;
        }
        return p1;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

反转单链表

反转单链表的迭代实现不是一个困难的事情，但是递归实现就有点难度了，如果再加一点难度，让你仅仅反转单链表中的一部分，你是否能够递归实现呢？

迭代的思路大概是：先用一个 for 循环找到第 m 个位置，然后再用一个 for 循环将 m 和 n 之间的元素反转。但是我们的递归解法不用一个 for 循环，纯递归实现反转。

迭代实现思路看起来虽然简单，但是细节问题很多的，反而不容易写对。相反，递归实现就很简洁优美，下面就由浅入深，先从反转整个单链表说起。

第二十五题力扣206题

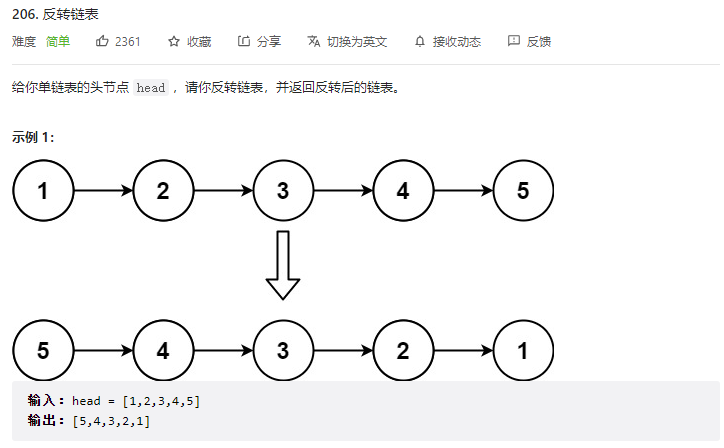
直接上代码：

ListNode reverse(ListNode head) {
    if (head == null || head.next == null) {
        return head;
    }
    ListNode last = reverse(head.next);
    head.next.next = head;
    head.next = null;
    return last;
}
1
2
3
4
5
6
7
8
9

看起来感觉不知所云，完全不能理解这样为什么能够反转链表？这就对了，这个算法常常拿来显示递归的巧妙和优美，我们下面来详细解释一下这段代码。

对于递归算法，最重要的就是明确递归函数的定义。具体来说，我们的 reverse 函数定义是这样的：

输入一个节点 head，将「以 head 为起点」的链表反转，并返回反转之后的头结点。

明白了函数的定义，再来看这个问题。比如说我们想反转这个链表：

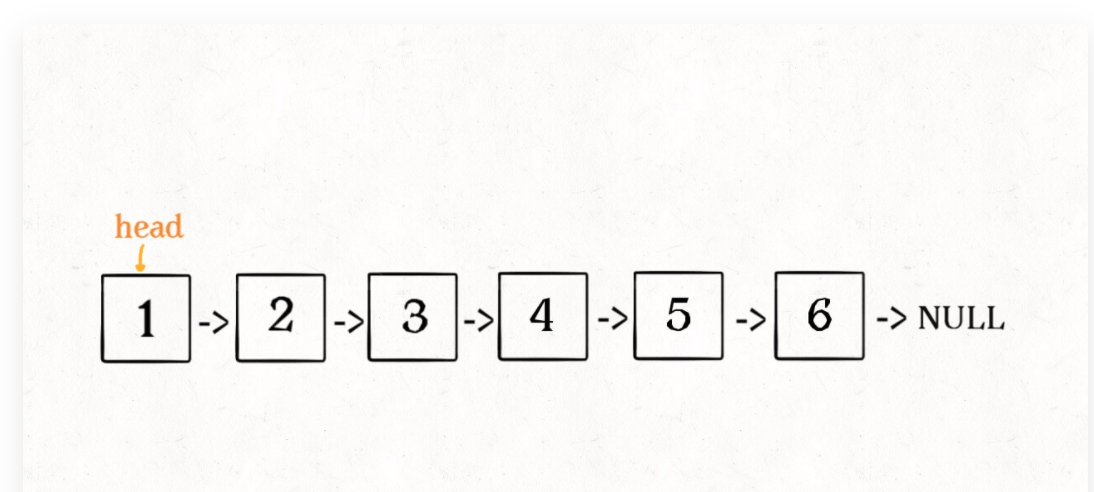
那么输入 reverse(head) 后，会在这里进行递归：

ListNode last = reverse(head.next);
1

不要跳进递归，而是要根据刚才的函数定义，来弄清楚这段代码会产生什么结果：

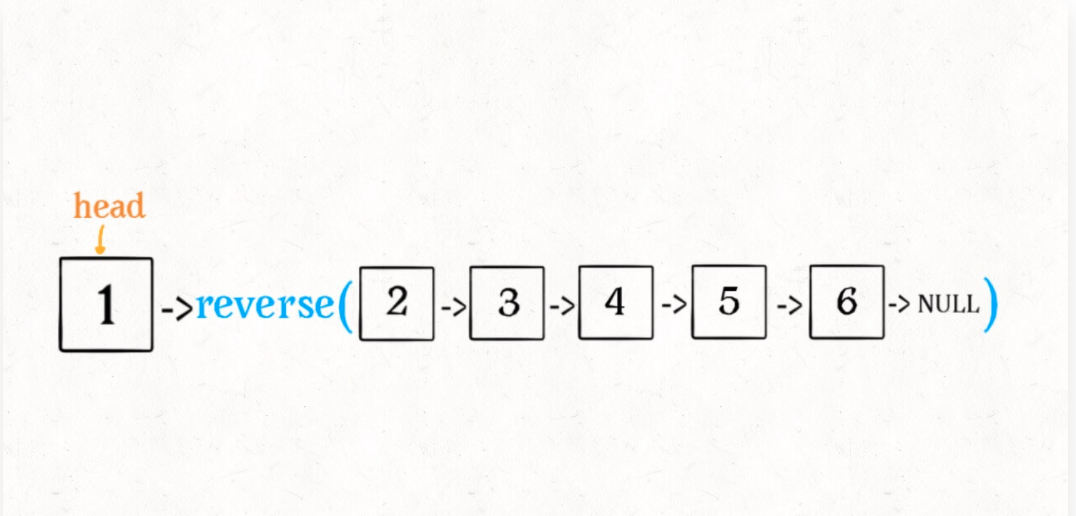
这个 reverse(head.next) 执行完成后，整个链表就成了这样：

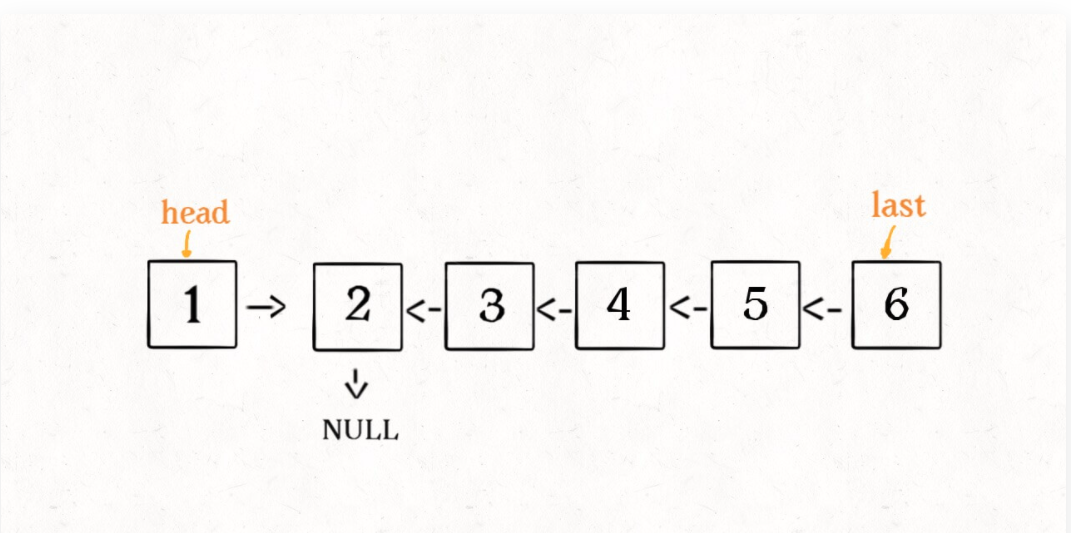
并且根据函数定义，reverse 函数会返回反转之后的头结点，我们用变量 last 接收了。

head.next.next = head;
1

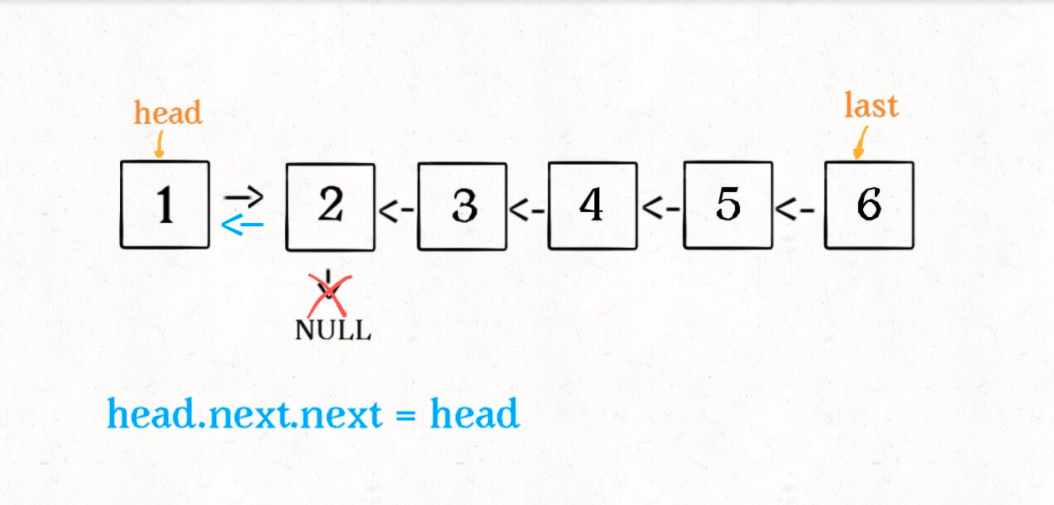
head.next = null;
return last;
1
2

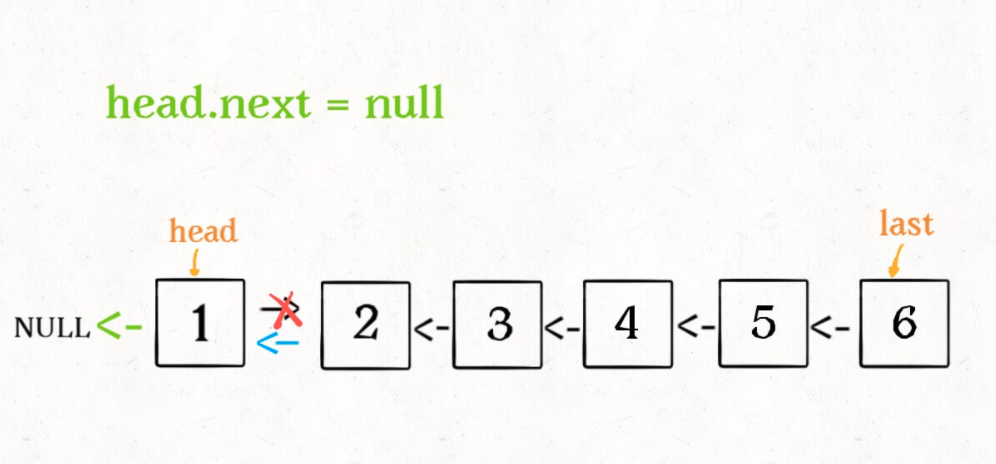
太神奇了！不过其中有两个地方需要注意：

1、递归函数要有 base case，也就是这句：

if (head.next == null) return head;
1

意思是如果链表只有一个节点的时候反转也是它自己，直接返回即可。

2、当链表递归反转之后，新的头结点是 last，而之前的 head 变成了最后一个节点，别忘了链表的末尾要指向 null：

head.next = null;
1

class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        if(head == nullptr||head->next == nullptr){
            return head;
        }
        ListNode *last = reverseList(head->next);
        head->next->next = head;
        head->next = nullptr;
        return last;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12

理解了这两点后，我们就可以进一步深入了，接下来的问题其实都是在这个算法上的扩展。

反转链表前 N 个节点

解决思路和反转整个链表差不多，只要稍加修改即可：

ListNode successor = null; // 后驱节点

// 反转以 head 为起点的 n 个节点，返回新的头结点
ListNode reverseN(ListNode head, int n) {
    if (n == 1) {
        // 记录第 n + 1 个节点
        successor = head.next;
        return head;
    }
    // 以 head.next 为起点，需要反转前 n - 1 个节点
    ListNode last = reverseN(head.next, n - 1);
    head.next.next = head;
    // 让反转之后的 head 节点和后面的节点连起来
    head.next = successor;
    return last;

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

1、base case 变为 n == 1，反转一个元素，就是它本身，同时要记录后驱节点。

2、刚才我们直接把 head.next 设置为 null，因为整个链表反转后原来的 head 变成了整个链表的最后一个节点。但现在 head 节点在递归反转之后不一定是最后一个节点了，所以要记录后驱 successor（第 n + 1 个节点），反转之后将 head 连接上。

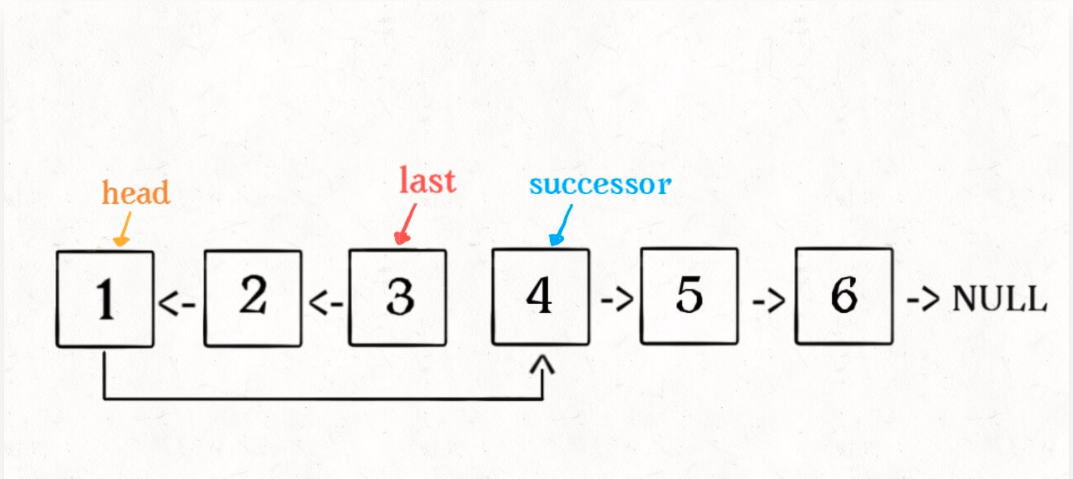
如果这个函数你也能看懂，就离实现「反转一部分链表」不远了。

反转链表的一部分

现在解决我们最开始提出的问题，给一个索引区间 [m,n]（索引从 1 开始），仅仅反转区间中的链表元素。

首先，如果 m == 1，就相当于反转链表开头的 n 个元素嘛，也就是我们刚才实现的功能：

如果 m != 1 怎么办？如果我们把 head 的索引视为 1，那么我们是想从第 m 个元素开始反转对吧；如果把 head.next 的索引视为 1 呢？那么相对于 head.next，反转的区间应该是从第 m - 1 个元素开始的；那么对于 head.next.next 呢……

区别于迭代思想，这就是递归思想，所以我们可以完成代码：

ListNode reverseBetween(ListNode head, int m, int n) {
    // base case
    if (m == 1) {
        return reverseN(head, n);
    }
    // 前进到反转的起点触发 base case
    head.next = reverseBetween(head.next, m - 1, n - 1);
    return head;
}
1
2
3
4
5
6
7
8
9

递归的思想相对迭代思想，稍微有点难以理解，处理的技巧是：不要跳进递归，而是利用明确的定义来实现算法逻辑。

处理看起来比较困难的问题，可以尝试化整为零，把一些简单的解法进行修改，解决困难的问题。

值得一提的是，递归操作链表并不高效。和迭代解法相比，虽然时间复杂度都是 O(N)，但是迭代解法的空间复杂度是 O(1)，而递归解法需要堆栈，空间复杂度是 O(N)。所以递归操作链表可以作为对递归算法的练习，但是考虑效率的话还是使用迭代算法更好。

第二十六题力扣92题

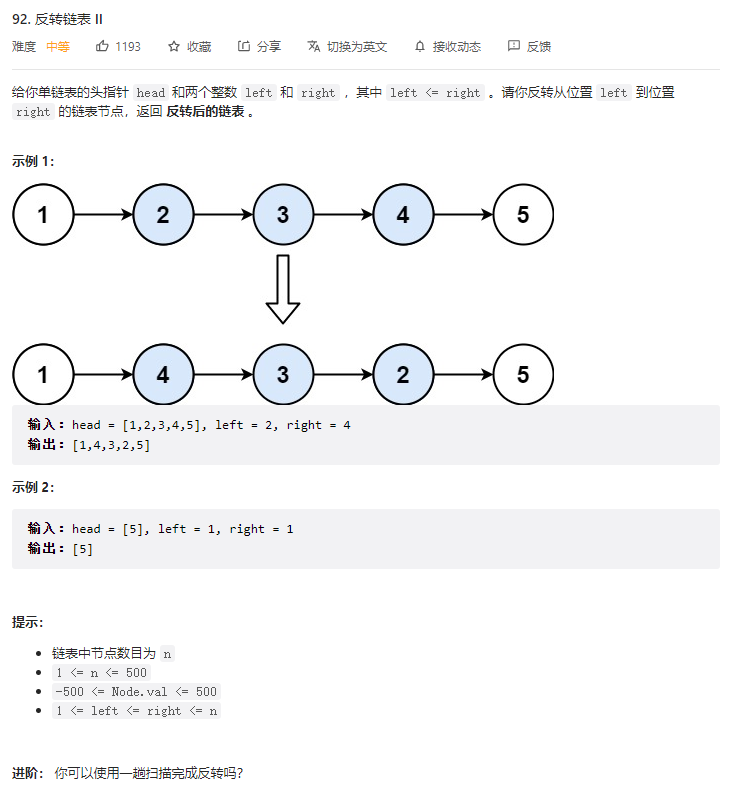
class Solution {
public:
    ListNode *back = nullptr;
    ListNode *reverse(ListNode *head,int n){
        if(n == 1){
            back = head->next;
            return head;
        }
        ListNode *last = reverse(head->next,n-1);
        head->next->next = head;
        head->next = back;
        return last;
    }

    ListNode* reverseBetween(ListNode* head, int left, int right) {
        if(left == 1){
            return reverse(head,right);
        }
        // 前进到反转的起点触发 base case
        head->next = reverseBetween(head->next,left-1,right-1);
        return head;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

JAVA参考

class Solution {
    ListNode successor = null; // 后驱节点

// 反转以 head 为起点的 n 个节点，返回新的头结点
ListNode reverseN(ListNode head, int n) {
    if (n == 1) {
        // 记录第 n + 1 个节点
        successor = head.next;
        return head;
    }
    // 以 head.next 为起点，需要反转前 n - 1 个节点
    ListNode last = reverseN(head.next, n - 1);
    head.next.next = head;
    // 让反转之后的 head 节点和后面的节点连起来
    head.next = successor;
    return last;
}
    public ListNode reverseBetween(ListNode head, int left, int right) {
        // base case
    if (left == 1) {
        return reverseN(head, right);
    }
    // 前进到反转的起点触发 base case
    head.next = reverseBetween(head.next, left - 1, right - 1);
    return head;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

判断有效括号串

对括号的有效性判断多次在笔试中出现，现实中也很常见，比如说我们写的代码，编辑器会检查括号是否正确闭合。而且我们的代码可能会包含三种括号 [](){}，判断起来有一点难度。

第二十七题力扣20题

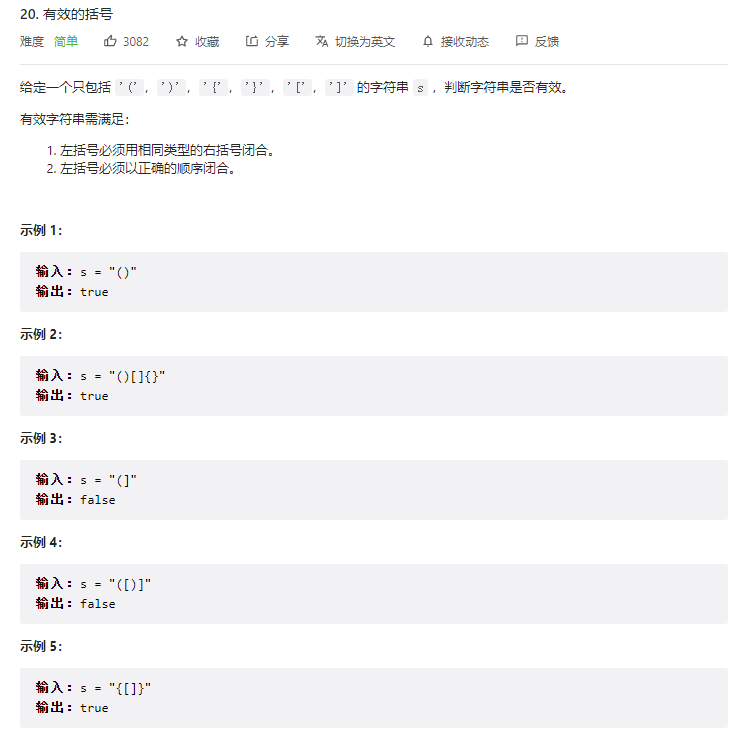
解决这个问题之前，我们先降低难度，思考一下，如果只有一种括号 ()，应该如何判断字符串组成的括号是否有效呢？

假设字符串中只有圆括号，如果想让括号字符串有效，那么必须做到：

每个右括号 ) 的左边必须有一个左括号 ( 和它匹配。

比如说字符串 ()))(( 中，中间的两个右括号左边就没有左括号匹配，所以这个括号组合是无效的。

bool isValid(string str) {
    // 待匹配的左括号数量
    int left = 0;
    for (int i = 0; i < str.size(); i++) {
        if (s[i] == '(') {
            left++;
        } else {
            // 遇到右括号
            left--;
        }

        // 右括号太多
        if (left == -1)
            return false;
    }
    // 是否所有的左括号都被匹配了
    return left == 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

如果只有圆括号，这样就能正确判断有效性。对于三种括号的情况，我一开始想模仿这个思路，定义三个变量 left1，left2，left3 分别处理每种括号，虽然要多写不少 if else 分支，但是似乎可以解决问题。

但实际上直接照搬这种思路是不行的，比如说只有一个括号的情况下 (()) 是有效的，但是多种括号的情况下， [(]) 显然是无效的。

仅仅记录每种左括号出现的次数已经不能做出正确判断了，我们要加大存储的信息量，可以利用栈来模仿类似的思路。栈是一种先进后出的数据结构，处理括号问题的时候尤其有用。

我们这道题就用一个名为 left 的栈代替之前思路中的 left 变量，遇到左括号就入栈，遇到右括号就去栈中寻找最近的左括号，看是否匹配：

bool isValid(string str) {
    stack<char> left;
    for (char c : str) {
        if (c == '(' || c == '{' || c == '[')
            left.push(c);
        else { // 字符 c 是右括号
            if (!left.empty() && leftOf(c) == left.top())
                left.pop();
            else
                // 和最近的左括号不匹配
                return false;
        }
    }
    // 是否所有的左括号都被匹配了
    return left.empty();
}

char leftOf(char c) {
    if (c == '}') return '{';
    if (c == ')') return '(';
    return '[';
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

第二十八题力扣921题

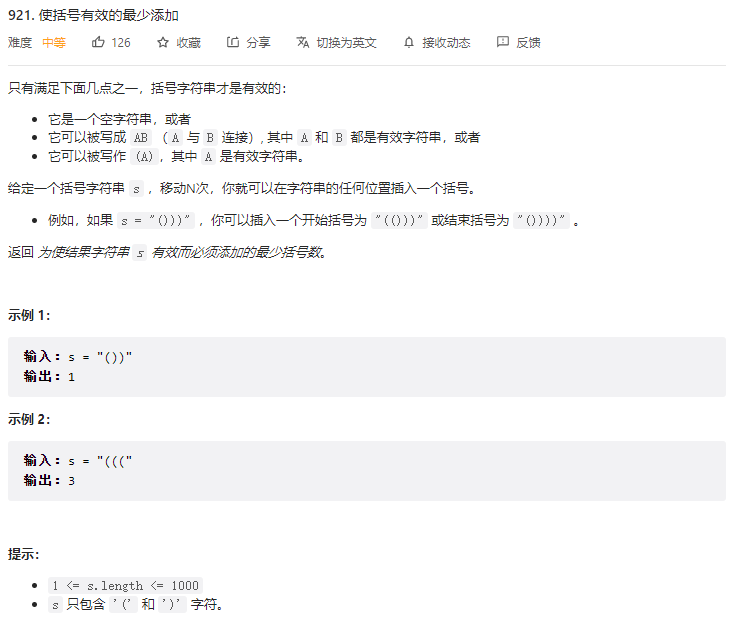
给你输入一个字符串 s，你可以在其中的任意位置插入左括号 ( 或者右括号 )，请问你最少需要几次插入才能使得 s 变成一个有效的括号串？

比如说输入 s = "())("，算法应该返回 2，因为我们至少需要插入两次把 s 变成 "(())()"，这样每个左括号都有一个右括号匹配，s 是一个有效的括号串。

int minAddToMakeValid(string s) {
    // res 记录插入次数
    int res = 0;
    // need 变量记录右括号的需求量
    int need = 0;
    for (int i = 0; i < s.size(); i++) {
        if (s[i] == '(') {
            // 对右括号的需求 + 1
            need++;
        }
        if (s[i] == ')') {
            // 对右括号的需求 - 1
            need--;
            if (need == -1) {
                need = 0;
                // 需插入一个左括号
                res++;
            }
        }
    }
    return res + need;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

这段代码就是最终解法，核心思路是以左括号为基准，通过维护对右括号的需求数 need，来计算最小的插入次数。需要注意两个地方：

1、当 need == -1 的时候意味着什么？

因为只有遇到右括号 ) 的时候才会 need--，need == -1 意味着右括号太多了，所以需要插入左括号。

比如说 s = "))" 这种情况，需要插入 2 个左括号，使得 s 变成 "（（））"，才是一个有效括号串。

2、算法为什么返回 res + need？

因为 res 记录的左括号的插入次数，need 记录了右括号的需求，当 for 循环结束后，若 need 不为 0，那么就意味着右括号还不够，需要插入。

比如说 s = "))(" 这种情况，插入 2 个左括号之后，还要再插入 1 个右括号，使得 s 变成 "()()()"，才是一个有效括号串。

以上就是这道题的思路，接下来我们看一道进阶题目，如果左右括号不是 1:1 配对，会出现什么问题

第二十九题力扣1541题

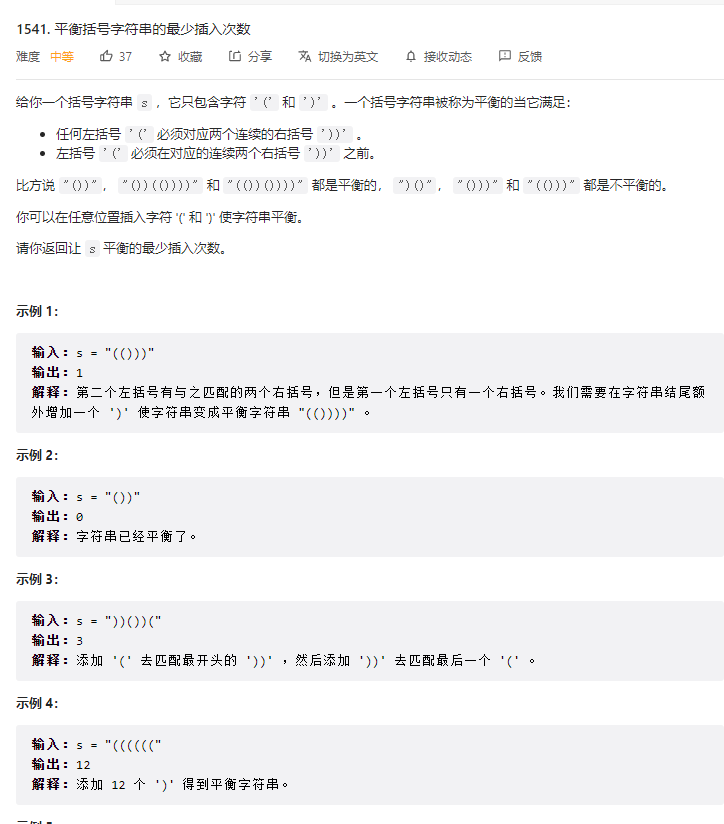
现在假设 1 个左括号需要匹配 2 个右括号才叫做有效的括号组合，那么给你输入一个括号串 s，请问你如何计算使得 s 有效的最小插入次数呢？

核心思路还是和刚才一样，通过一个 need 变量记录对右括号的需求数，根据 need 的变化来判断是否需要插入。

第一步，我们按照刚才的思路正确维护 need 变量：

int minInsertions(string s) {
    // need 记录需右括号的需求量
    int res = 0, need = 0;
    for (int i = 0; i < s.size(); i++) {
        // 一个左括号对应两个右括号
        if (s[i] == '(') {
            need += 2;
        }
        if (s[i] == ')') {
            need--;
        }
    }
    return res + need;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14

现在想一想，当 need 为什么值的时候，我们可以确定需要进行插入？

首先，类似第一题，当 need == -1 时，意味着我们遇到一个多余的右括号，显然需要插入一个左括号。

比如说当 s = ")"，我们肯定需要插入一个左括号让 s = "()"，但是由于一个左括号需要两个右括号，所以对右括号的需求量变为 1：

if (s[i] == ')') {
    need--;
    // 说明右括号太多了
    if (need == -1) {
        // 需要插入一个左括号
        res++;
        // 同时，对右括号的需求变为 1
        need = 1;
    }
}
1
2
3
4
5
6
7
8
9
10

另外，当遇到左括号时，若对右括号的需求量为奇数，需要插入 1 个右括号。因为一个左括号需要两个右括号嘛，右括号的需求必须是偶数，这一点也是本题的难点。

所以遇到左括号时要做如下判断：

if (s[i] == '(') {
    need += 2;
    if (need % 2 == 1) {
        // 插入一个右括号
        res++;
        // 对右括号的需求减一
        need--;
    }
}
1
2
3
4
5
6
7
8
9

所以答案为：

int minInsertions(string s) {
    int res = 0, need = 0;
    for (int i = 0; i < s.size(); i++) {
        if (s[i] == '(') {
            need += 2;
            if (need % 2 == 1) {
                res++;
                need--;
            }
        }
        if (s[i] == ')') {
            need--;
            if (need == -1) {
                res++;
                need = 1;
            }
        }
    }
    return res + need;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

队列实现栈以及栈实现队列

这两种数据结构底层其实都是数组或者链表实现的，只是 API 限定了它们的特性

第三十题力扣232题

我们使用两个栈 s1, s2 就能实现一个队列的功能，当调用 push 让元素入队时，只要把元素压入 s1 即可，那么如果这时候使用 peek 查看队头的元素怎么办呢？按道理队头元素应该是 1，但是在 s1 中 1 被压在栈底，现在就要轮到 s2 起到一个中转的作用了：当 s2 为空时，可以把 s1 的所有元素取出再添加进 s2，这时候 s2 中元素就是先进先出顺序了。

同理，对于 pop 操作，只要操作 s2 就可以了。最后，如何判断队列是否为空呢？如果两个栈都为空的话，就说明队列为空。

class MyQueue {
private:
    stack<int> inStack, outStack;

    void in2out() {
        while (!inStack.empty()) {
            outStack.push(inStack.top());
            inStack.pop();
        }
    }

public:
    MyQueue() {}

    void push(int x) {
        inStack.push(x);
    }

    int pop() {
        if (outStack.empty()) {
            in2out();
        }
        int x = outStack.top();
        outStack.pop();
        return x;
    }

    int peek() {
        if (outStack.empty()) {
            in2out();
        }
        return outStack.top();
    }

    bool empty() {
        return inStack.empty() && outStack.empty();
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

第三十一题力扣225题

1.先说 push API，直接将元素加入队列，同时记录队尾元素，因为队尾元素相当于栈顶元素，如果要 top 查看栈顶元素的话可以直接返回

2.我们的底层数据结构是先进先出的队列，每次 pop 只能从队头取元素；但是栈是后进先出，也就是说 pop API 要从队尾取元素

3.解决方法简单粗暴，把队列前面的都取出来再加入队尾，让之前的队尾元素排到队头，这样就可以取出了

queue<int> q;

    /** Initialize your data structure here. */
    MyStack() {

    }

    /** Push element x onto stack. */
    void push(int x) {
        int n = q.size();
        q.push(x);
        for (int i = 0; i < n; i++) {
            q.push(q.front());
            q.pop();
        }
    }
    
    /** Removes the element on top of the stack and returns that element. */
    int pop() {
        int r = q.front();
        q.pop();
        return r;
    }
    
    /** Get the top element. */
    int top() {
        int r = q.front();
        return r;
    }
    
    /** Returns whether the stack is empty. */
    bool empty() {
        return q.empty();
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

单调栈

栈（stack）是很简单的⼀种数据结构，先进后出的逻辑顺序，符合某些问题的特点，⽐如说函数调⽤栈。单调栈实际上就是栈，只是利⽤了⼀些巧妙的逻辑，使得每次新元素⼊栈后，栈内的元素都保持有序（单调递增或单调递减）。听起来有点像堆（heap）？不是的，单调栈⽤途不太⼴泛，只处理⼀种典型的问题，叫做 Next Greater Element。本⽂⽤讲解单调队列的算法模版解决这类问题，并且探讨处理「循环数组」的策略。

单调栈模板

现在给你出这么⼀道题：给你⼀个数组 nums，请你返回⼀个等⻓的结果数组，结果数组中对应索引存储着下⼀个更⼤元素，如果没有更⼤的元素，就存 -1。

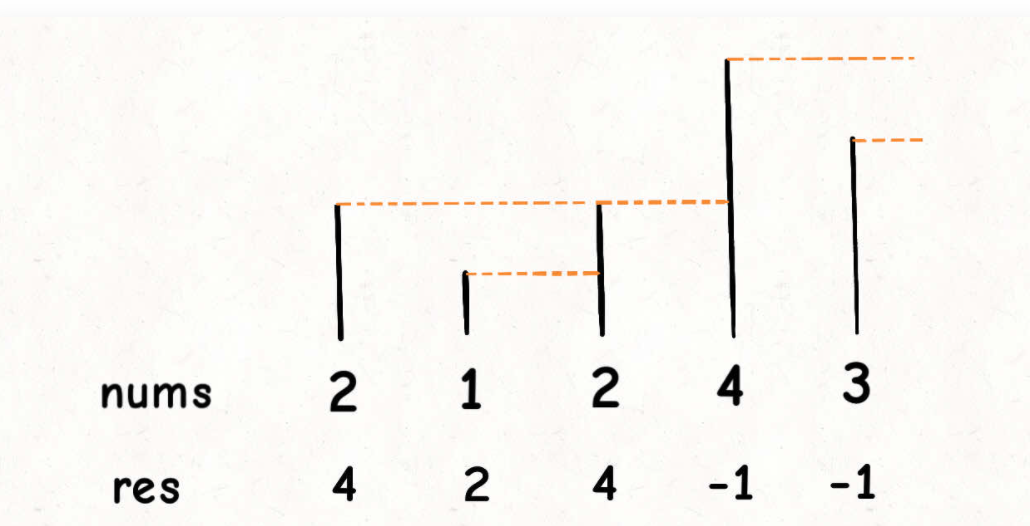
比如说，输入一个数组 nums = [2,1,2,4,3]，你返回数组 [4,2,4,-1,-1]。

解释：第一个 2 后面比 2 大的数是 4; 1 后面比 1 大的数是 2；第二个 2 后面比 2 大的数是 4; 4 后面没有比 4 大的数，填 -1；3 后面没有比 3 大的数，填 -1。

这道题的暴力解法很好想到，就是对每个元素后面都进行扫描，找到第一个更大的元素就行了。但是暴力解法的时间复杂度是 O(n^2)。

代码：

vector<int> nextGreaterElement(vector<int>& nums) {
    vector<int> res(nums.size()); // 存放答案的数组
    stack<int> s;
    // 倒着往栈里放
    for (int i = nums.size() - 1; i >= 0; i--) {
        // 判定个子高矮
        while (!s.empty() && s.top() <= nums[i]) {
            // 矮个起开，反正也被挡着了。。。
            s.pop();
        }
        // nums[i] 身后的 next great number
        res[i] = s.empty() ? -1 : s.top();
        s.push(nums[i]);
    }
    return res;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

这就是单调队列解决问题的模板。for 循环要从后往前扫描元素，因为我们借助的是栈的结构，倒着入栈，其实是正着出栈。while 循环是把两个「个子高」元素之间的元素排除，因为他们的存在没有意义，前面挡着个「更高」的元素，所以他们不可能被作为后续进来的元素的 Next Great Number 了。

这个算法的时间复杂度不是那么直观，如果你看到 for 循环嵌套 while 循环，可能认为这个算法的复杂度也是 O(n^2)，但是实际上这个算法的复杂度只有 O(n)。

分析它的时间复杂度，要从整体来看：总共有 n 个元素，每个元素都被 push 入栈了一次，而最多会被 pop 一次，没有任何冗余操作。所以总的计算规模是和元素规模 n 成正比的，也就是 O(n) 的复杂度。

第三十二题力扣739题

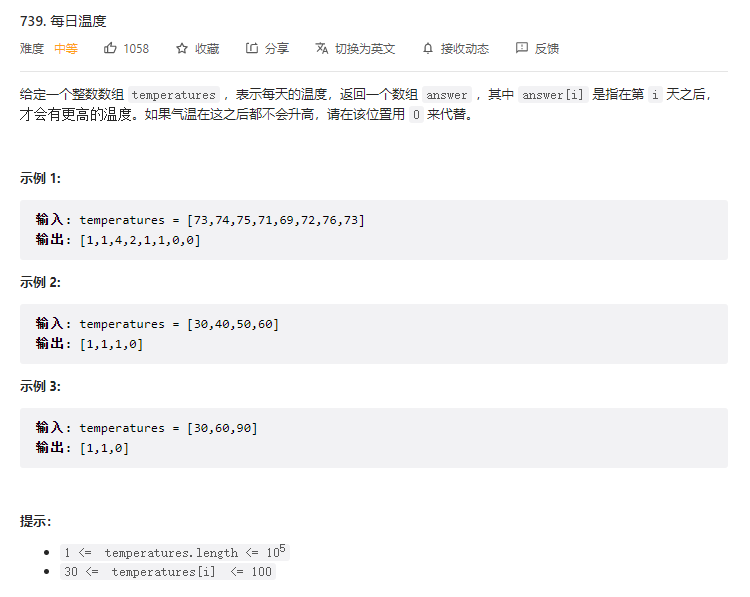
给你一个数组 T，这个数组存放的是近几天的天气气温，你返回一个等长的数组，计算：对于每一天，你还要至少等多少天才能等到一个更暖和的气温；如果等不到那一天，填 0。

比如说给你输入 T = [73,74,75,71,69,76]，你返回 [1,1,3,2,1,0]。

这个问题本质上也是找 Next Greater Number，只不过现在不是问你 Next Greater Number 是多少，而是问你当前距离 Next Greater Number 的距离而已。

相同的思路，直接调用单调栈的算法模板，稍作改动就可以，直接上代码

vector<int> dailyTemperatures(vector<int>& T) {
    vector<int> res(T.size());
    // 这里放元素索引，而不是元素
    stack<int> s; 
    /* 单调栈模板 */
    for (int i = T.size() - 1; i >= 0; i--) {
        while (!s.empty() && T[s.top()] <= T[i]) {
            s.pop();
        }
        // 得到索引间距
        res[i] = s.empty() ? 0 : (s.top() - i); 
        // 将索引入栈，而不是元素
        s.push(i); 
    }
    return res;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

如何处理环形数组

同样是 Next Greater Number，现在假设给你的数组是个环形的，如何处理？

第三十三题力扣503题

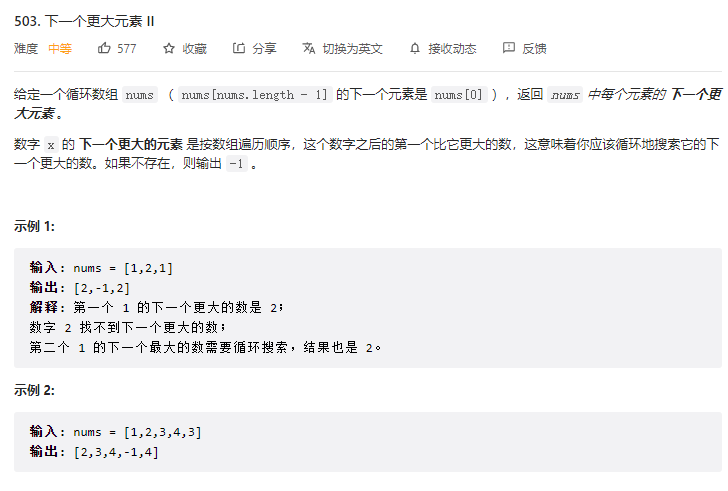
比如输入一个数组 [2,1,2,4,3]，你返回数组 [4,2,4,-1,4]。拥有了环形属性，最后一个元素 3 绕了一圈后找到了比自己大的元素 4。

一般是通过 % 运算符求模（余数），来获得环形

int[] arr = {1,2,3,4,5};
int n = arr.length, index = 0;
while (true) {
    print(arr[index % n]);
    index++;
}
1
2
3
4
5
6

这个问题肯定还是要用单调栈的解题模板，但难点在于，比如输入是 [2,1,2,4,3]，对于最后一个元素 3，如何找到元素 4 作为 Next Greater Number。

对于这种需求，常用套路就是将数组长度翻倍

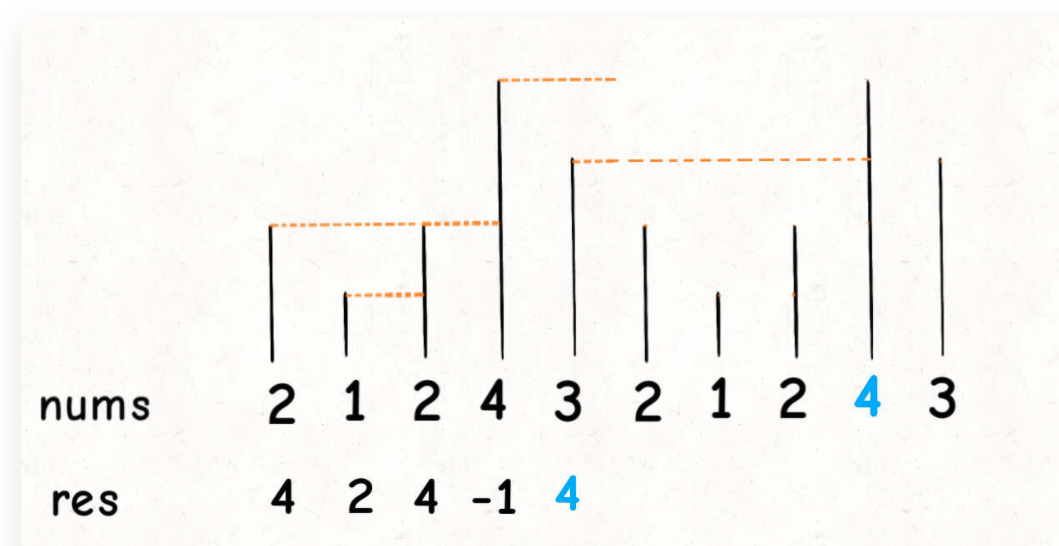
有了思路，最简单的实现方式当然可以把这个双倍长度的数组构造出来，然后套用算法模板。但是，我们可以不用构造新数组，而是利用循环数组的技巧来模拟数组长度翻倍的效果。

vector<int> nextGreaterElements(vector<int>& nums) {
    int n = nums.size();
    vector<int> res(n);
    stack<int> s;
    // 假装这个数组长度翻倍了
    for (int i = 2 * n - 1; i >= 0; i--) {
        // 索引要求模，其他的和模板一样
        while (!s.empty() && s.top() <= nums[i % n]) {
            s.pop();
        }
        res[i % n] = s.empty() ? -1 : s.top();
        s.push(nums[i % n]);
    }
    return res;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/我家自动化/article/detail/63477

算法刷题记录1_对一数组进行逐步累加求和,prefix代表从前向后累加值, suffix代表从后向前累加值,

第一题CSP202112-1题

解题思路

$$ sum(A)

第二题CSP20219-1题

解题思路

第三题 力扣第二题

解题

第四题 力扣第三题

前提：滑动窗口及哈希表

题目

解题：

第五题

1.⼀维数组中的前缀和 力扣303题

第六题

2.二维矩阵中的前缀和 力扣304题

第七题

3.和为k的子数组 力扣560题

JAVA 哈希图

第八题

差分数组

题目：区间加法 力扣370题

第九题 力扣1109题

第十题 力扣1094题

滑动窗口改进

第十一题 力扣76题

第十二题 力扣567题

第十三题 力扣438题

二分查找

⼆分搜索问题的泛化

第十四题 力扣875题

第十五题 力扣1101题

原地修改数组

有序数组/链表去重 力扣26题 第十六题

第十七题 力扣第 83 题

第十八题 力扣第27题

第十九题 力扣第283题

单链表及技巧

第二十题 力扣21题

第二十一题 力扣23题

使用优先队列合并

单链表的倒数第 k 个节点

第二十三题 力扣19题

单链表的中点

第二十四题 力扣876题

方法二 数组

判断链表是否包含环

两个链表是否相交

反转单链表

第二十五题 力扣206题

反转链表前 N 个节点

反转链表的一部分

第二十六题 力扣92题

判断有效括号串

第二十七题 力扣20题

第二十八题 力扣921题

第二十九题 力扣1541题

队列实现栈以及栈实现队列

第三十题 力扣232题

第三十一题 力扣225题

单调栈

单调栈模板

第三十二题 力扣739题

如何处理环形数组

第三十三题 力扣503题

$$
sum(A)

第三题力扣第二题

第四题力扣第三题

1.⼀维数组中的前缀和力扣303题

2.二维矩阵中的前缀和力扣304题

3.和为k的子数组力扣560题

题目：区间加法力扣370题

第九题力扣1109题

第十题力扣1094题

第十一题力扣76题

第十二题力扣567题

第十三题力扣438题

第十四题力扣875题

第十五题力扣1101题

有序数组/链表去重力扣26题第十六题

第十七题力扣第 83 题

第十八题力扣第27题

第十九题力扣第283题

第二十题力扣21题

第二十一题力扣23题

第二十三题力扣19题

第二十四题力扣876题

方法二数组

第二十五题力扣206题

第二十六题力扣92题

第二十七题力扣20题

第二十八题力扣921题

第二十九题力扣1541题

第三十题力扣232题

第三十一题力扣225题

第三十二题力扣739题

第三十三题力扣503题