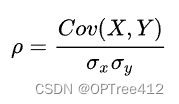PCA降维（主成分分析法）_pca中pc1和pc2多少合适

PCA的基本思想

主成分分析法就是找出数据里最主要的方面，用数据里最主要的方面来代替原始数据。说直白点就是将数据从n维降到n’维，并且希望n’维特征的数据集尽可能的保留大部分信息。

PCA数学推导（最大方差法）

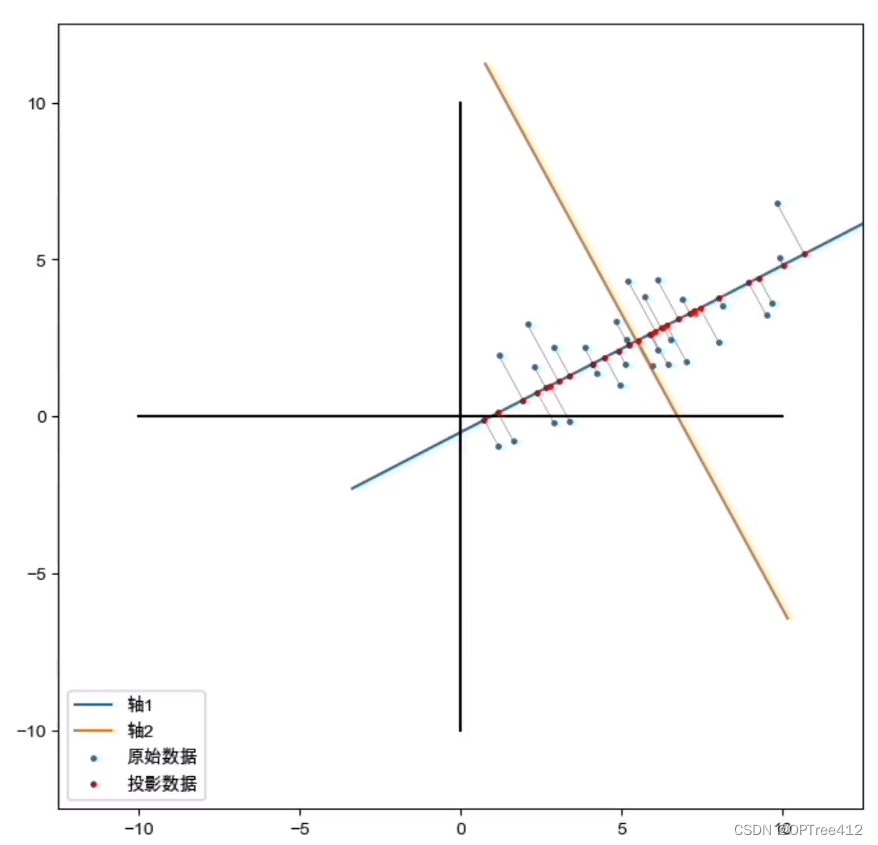
举个数据是二维的李子，我们将原始数据（蓝点）投影到新的最标轴上（黄蓝十字线）。寻找这个新坐标轴的方式就是要找到数据投影在新坐标轴上的点（红点）到新坐标轴原点的距离最大的时候，这就最大方差法。

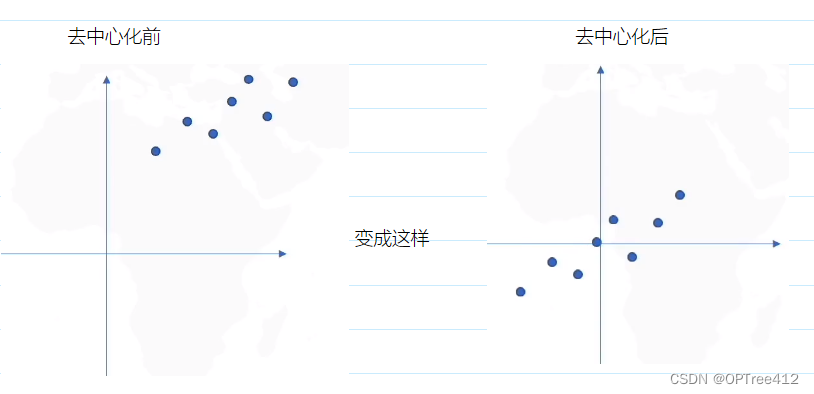
第一步，数据去中心化

新坐标轴，旧坐标轴的讨论好麻烦，我们直接把数据去中心化（就是数据的均值在远点上）。如果数据不去中心化，我们是找不到最优降维的。这步是必须的

第二步，找到新最标轴

我们怎么找到最佳的那个最标轴来实现主成分分析呢？
就是通过投影后的点到坐标轴原点之间的距离越大越好（这就是最大方差）

如图，红色虚线是新的坐标轴，我们叫它PC1；绿色圆点就是一开始的数据样本点；绿叉就是投影在新坐标上的点；d1,d2,d3…d6这些就是投影后的点到远点的距离。

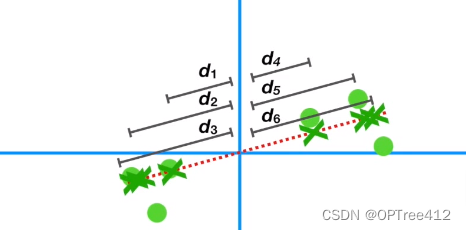
我们需要做的就是找到最大的平方和（就是∑di^2）。

这里要开始数学计算了！！！！

从上图可知，我们在进行寻找最佳新最标轴时，实际上就是通过求出数据相关系数矩阵来寻找特征值和特征向量。

第三步，选择你需要数据的百分之几的成分

我们在进行PCA降维寻找新坐标的时候，这个坐标个数和数据特征数是相同的。但是我们将数据投影在新的坐标轴上，就是为了能用尽可能少的特征来表达整个数据的信息。

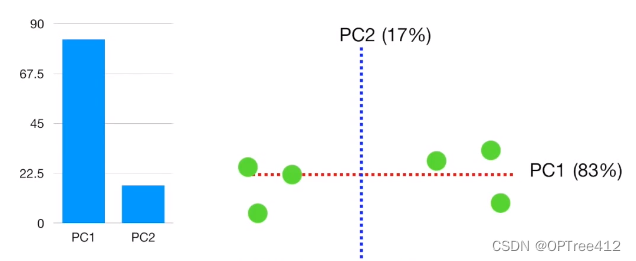
下图我们可以看到我们分别获得PC1和PC2两个坐标轴，两个坐标轴是相互垂直的，互不干扰。
其中PC1上数据的信息占83%，PC2上数据的信息占17%。谁都能看出来应该选择哪个坐标轴来代表降维后的信息。

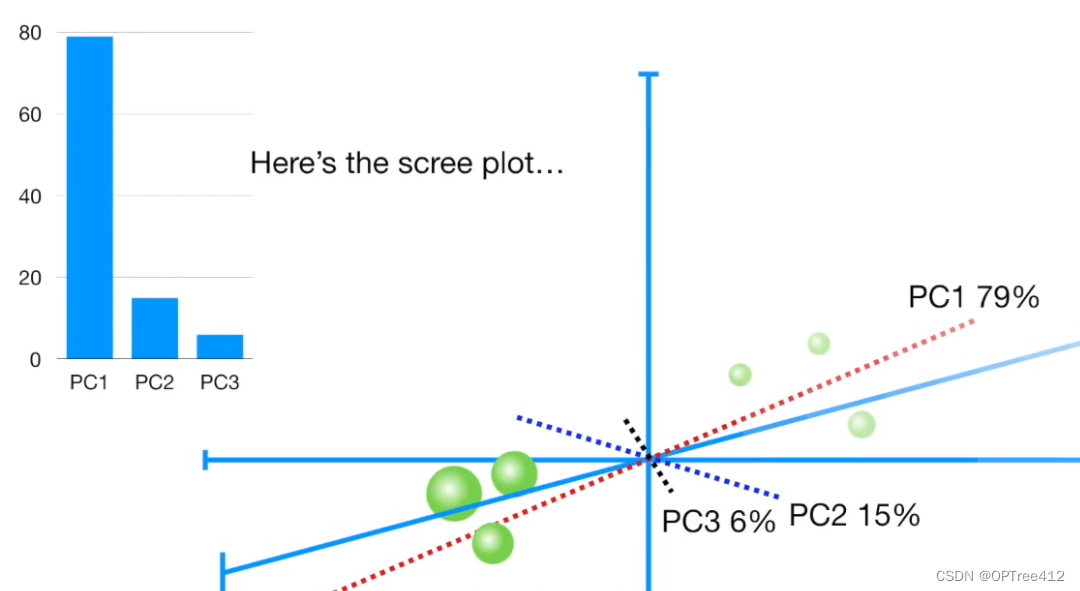
我们看看三维的时候，可以看出如果要将为我们用PC1和PC2来降维

PCA算法的优劣

作为一个非监督学习的降维方法，它只需要特征值分解，就可以对数据进行压缩，去噪。因此在实际场景应用很广泛。

PCA算法的主要优点有：

1）仅仅需要以方差衡量信息量，不受数据集以外的因素影响。

2）各主成分之间正交，可消除原始数据成分间的相互影响的因素。

3）计算方法简单，主要运算是特征值分解，易于实现。

PCA算法的主要缺点有：

1）主成分各个特征维度的含义具有一定的模糊性，不如原始样本特征的解释性强。

2）方差小的非主成分也可能含有对样本差异的重要信息，因降维丢弃可能对后续数据处理有影响。
3）当数据分布不属于正态分布的时候，效果不是很好

问题

1.为什么要平方呢？是因为不平方的话距离有正有负，会相互抵消。
2.**为什么时相关系数矩阵而不是协方差矩阵呢？**这个往下看你就知道了

使用PCA到底需不需要去量纲呢？

（1）当：各个属性单位相同时（比如，都是kg，都是米），各个属性是可比较的。因此直接求属性与属性之间的协方差即可。原本协方差的大小并不说明相关程度（协方差只表示正相关还是负相关），但是在单位相同时候，我们可以认为协方差越大，相关性越大。

（2）当：各个属性单位不同时，（比如，一个是kg，一个是米）这个时候，由于单位不同，协方差不表示相关程度，这时候，我们就要使用相关系数来进行描述。

相关系数的公式（就是相关系数矩阵除以两个标准差，其中除以标准差就是一种去量纲的方式）。它消除了两个变量变化幅度的影响，而只是单纯反应两个变量每单位变化时的相似程度。