图解RoPE旋转位置编码及其特性

来自：YeungNLP

直播 | LLMs时代下，前沿领域的最新研究

01

前言

旋转位置编码RoPE (Rotary Position Embedding) 是目前大模型中广泛使用的一种位置编码，包括但不限于Llama、Baichuan、ChatGLM、Qwen等。由于计算资源限制，目前的大模型大多在较小的上下文长度中进行训练，在推理中，若超出预训练的长度，模型的性能将会显著降低。于是涌现出了许多基于RoPE的长度外推的工作，旨在让大模型能够在预训练长度之外，取得更好的效果。所以弄清楚RoPE的底层原理，对于RoPE-base模型进行长度外推至关重要。

本文主要结合苏神关于Roformer的论文与博客进行介绍。在原博客和论文中，苏神更多的是以复数的形式推导和介绍RoPE，本文将主要从向量旋转的角度对RoPE进行介绍，并且结合函数图像，以数形结合的方式帮助大家更直观地理解RoPE的各种性质。

02

为什么需要位置编码？

众所周知，transformer模型之所以能够取得如此卓越的效果，其中的Attention机制功不可没，它的本质是计算输入序列中的每个token与整个序列的注意力权重。假设  和  分别表示词向量  位于位置  和词向量  位于位置  ，在未添加位置信息的时候，  ，则两者的注意力权重计算如下:

我们会发现，在未加入位置信息的情况下，无论  和  所处的位置如何变化，它们之间的注意力权重  均不会发生变化，也就是位置无关，这显然与我们的直觉不符。对于两个词向量，如果它们之间的距离较近，我们希望它们之间的的注意力权重更大，当距离较远时，注意力权重更小。

为了解决这个问题，我们需要为模型引入位置编码，让每个词向量都能够感知到它在输入序列中所处的位置信息。我们定义如下函数，该函数表示对词向量  注入位置信息  ，得到  ：

则  与  之间的注意力权重可表示为：

03

绝对位置编码

我们先简单回顾一下经典的绝对位置编码，主要包括训练式位置编码与Sinusoidal位置编码。

训练式位置编码

训练式位置编码，顾名思义就是每个位置的位置向量会随着模型一起训练。假设模型最大输入长度为512，向量维度为768，我们可初始化一个512*768的位置编码矩阵，该矩阵将参与模型的训练，从而学习得到每个位置所对应的向量表示。

如何为每个位置的词向量注入位置信息呢？答案是相加，如以下公式所示，其中  表示第  个位置的位置向量：

训练式位置编码广泛应用于早期的transformer类型的模型，如BERT、GPT、ALBERT等。但其缺点是模型不具有长度外推性，因为位置编码矩阵的大小是预设的，若对其进行扩展，将会破坏模型在预训练阶段学习到的位置信息。例如将512*768扩展为1024*768，新拓展的512个位置向量缺乏训练，无法正确表示512~1023的位置信息。但早期大家对长文本输入的需求并不如现在迫切。

Sinusoidal位置编码

Sinusoidal位置编码是谷歌在Transformer模型中提出的一种绝对位置编码，它的形式如下，其中  表示词向量的维度，  表示位置索引，  和  表示位置向量的分量索引，例如  和  分别表示位置  的位置向量的第  和第  个分量：

Sinusoidal位置编码的每个分量都是正弦或余弦函数，所有每个分量的数值都具有周期性。如下图所示，每个分量都具有周期性，并且越靠后的分量，波长越长，频率越低。这是一个非常重要的性质，基于RoPE的大模型的长度外推工作，与该性质有着千丝万缕的关联，后续我们会进行分享。

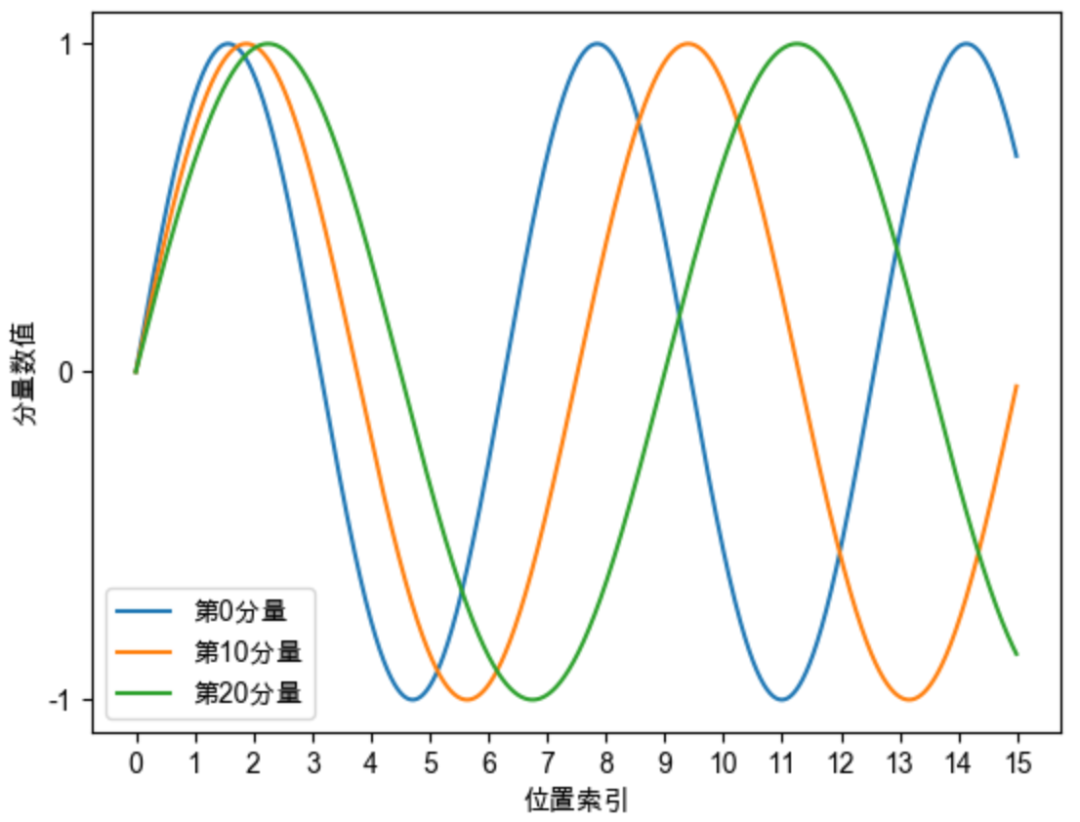
Sinusoidal位置编码还具有远程衰减的性质，具体表现为：对于两个相同的词向量，如果它们之间的距离越近，则他们的内积分数越高，反之则越低。如下图所示，我们随机初始化两个向量q和k，将q固定在位置0上，k的位置从0开始逐步变大，依次计算q和k之间的内积。我们发现随着q和k的相对距离的增加，它们之间的内积分数震荡衰减。

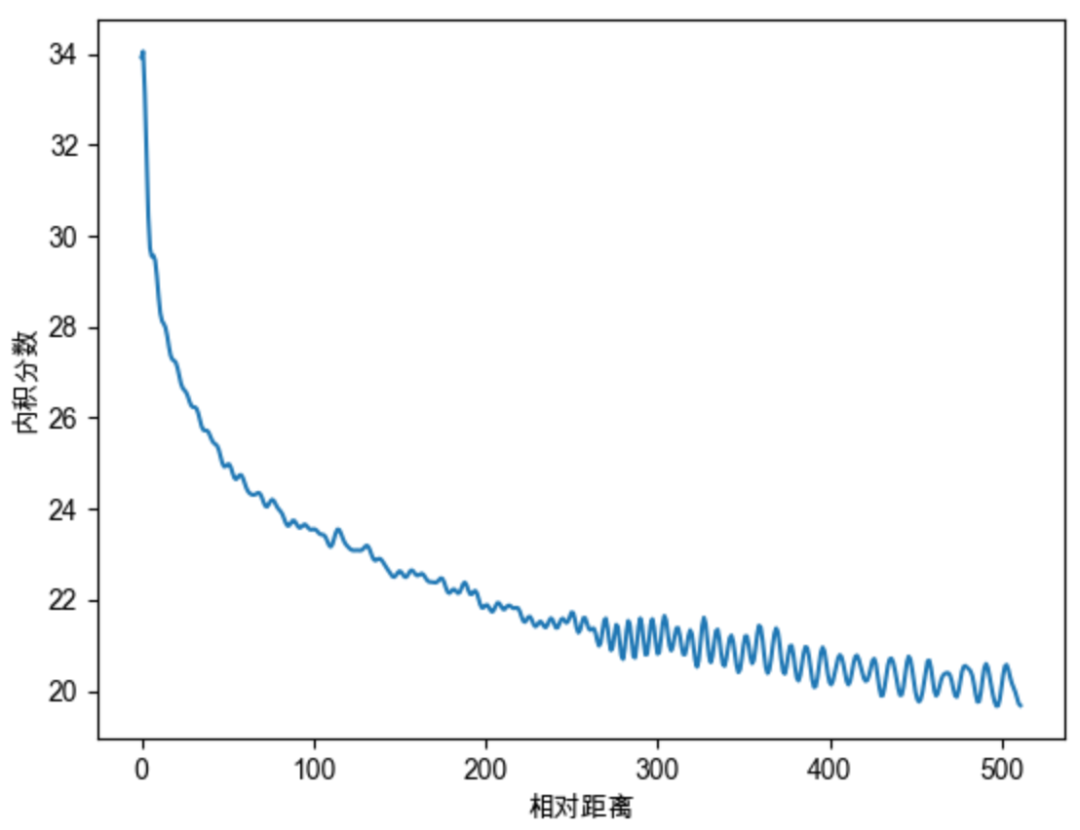
因为Sinusoidal位置编码中的正弦余弦函数具备周期性，并且具备远程衰减的特性，所以理论上也具备一定长度外推的能力。

04

RoPE位置编码

在这里先直接抛出一个直观的结论：RoPE位置编码通过将一个向量旋转某个角度，为其赋予位置信息。

RoPE的出发点

接下来进入今天的主角RoPE位置编码。在绝对位置编码中，尤其是在训练式位置编码中，模型只能感知到每个词向量所处的绝对位置，并无法感知两两词向量之间的相对位置。对于Sinusoidal位置编码而言，这一点得到了缓解，模型一定程度上能够感知相对位置。

对于RoPE而言，作者的出发点为：通过绝对位置编码的方式实现相对位置编码。回顾我们此前定义的位置编码函数，该函数表示对词向量  添加绝对位置信息  ，得到  ：

RoPE希望  与  之间的点积，即  中能够带有相对位置信息  。那么  如何才算带有相对位置信息呢？只需要能够将  表示成一个关于  、  、  的函数  即可，其中  便表示着两个向量之间的相对位置信息。

因此我们建模的目标就变成了：找到一个函数  ，使得如下关系成立:

二维位置编码

为了简化问题，我们先假设词向量是二维的。作者借助复数来进行求解，在此我们省略求解过程，直接抛出答案，最终作者得到如下位置编码函数，其中  为位置下标，  为一个常数： 为了更好地理解上面的函数，我们先简单复习一下线性代数中的旋转矩阵。在二维空间中，存在一个旋转矩阵  ，当一个二维向量左乘旋转矩阵时，该向量即可实现弧度为  的逆时针旋转操作。 

我们以二维向量  为例，将其逆时针旋转45度，弧度为  ，将得到新的二维向量  ，向量的模长未发生改变，仍然是1。计算过程如下： 

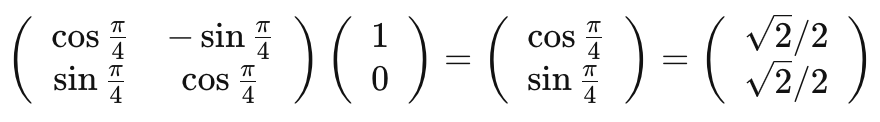
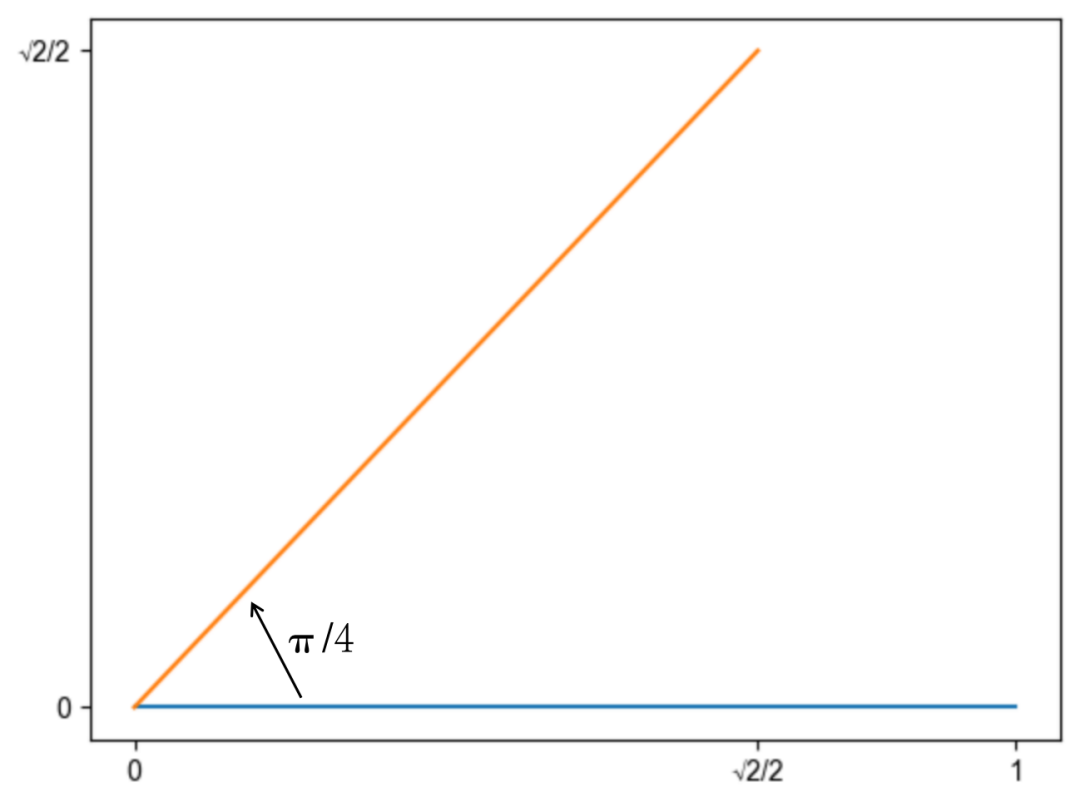
回看我们求解得到的位置编码函数  ，感叹数学之美，我们得到的是一个向量旋转的函数，左侧的  是一个旋转矩阵，  表示在保持向量  的模长的同时，将其逆时针旋转  。这意味着只需要将向量旋转某个角度，即可实现对该向量添加绝对位置信息，这就是旋转位置编码的由来。

我们进一步验证RoPE是否能通过绝对位置编码的方式实现相对位置编码。当我们求两个向量之间的点积会发现，它们的点积是一个关于  、  、  的函数  ，所以函数  实现了以绝对位置编码的方式实现相对位置编码。 

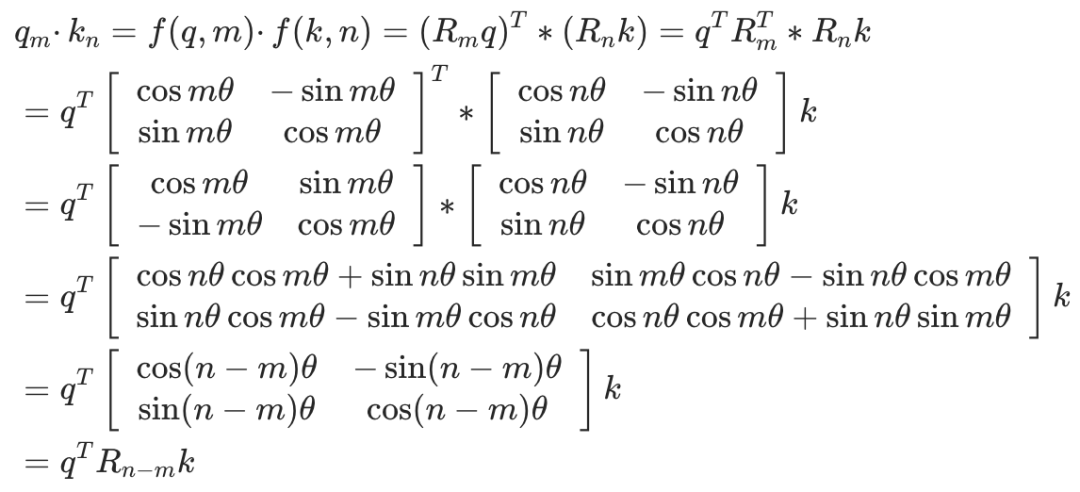
为了更加形象生动地理解旋转位置编码，我们结合图形描述如何为一个二维向量赋予位置编码。假设存在向量  ，位置编码函数  中的  是一个常量，我们不妨设为1，则： 

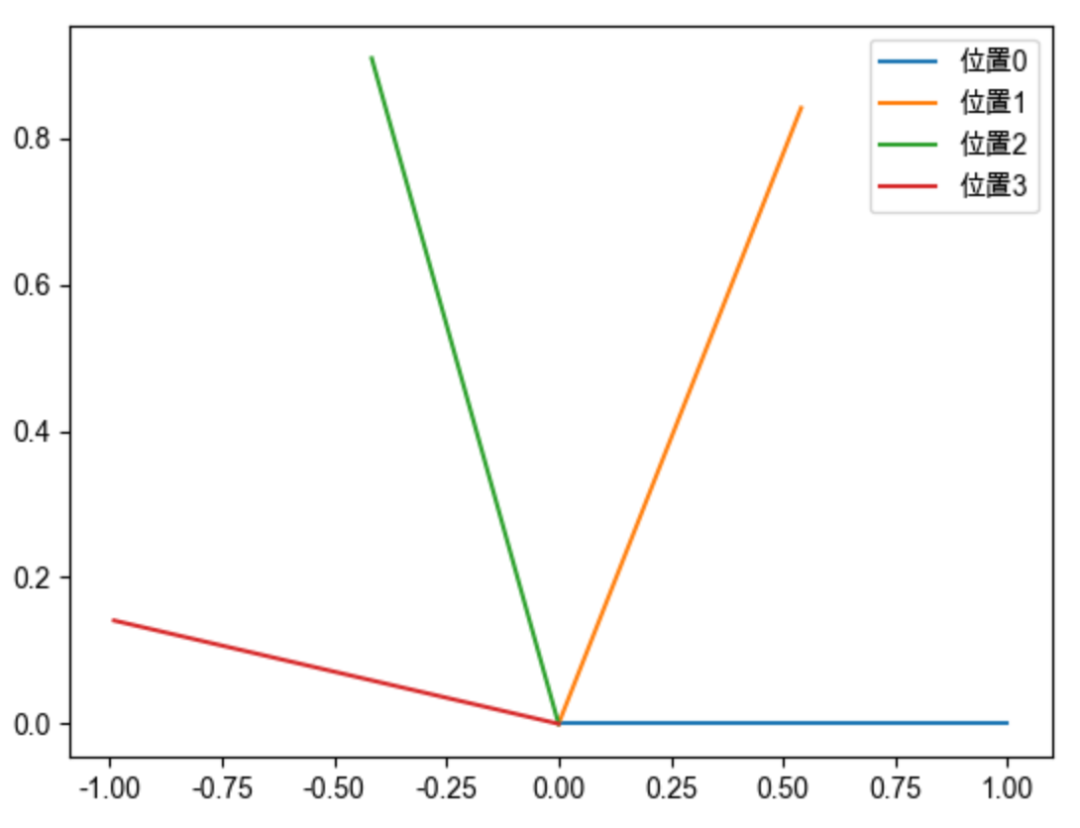
向量  位于位置0,1,2,3时，分别将向量  旋转0,1,2,3弧度，就可以为其赋予对应的绝对位置信息。如下图所示，只需要对向量进行旋转操作，即可对向量添加对应的位置信息。并且向量旋转具有周期性。

到此为止，我们已经弄明白了旋转位置编码的来源、数学意义，以及它是如何使用绝对位置实现相对位置编码，大道至简，惊叹数学的优雅。

推广到多维

上述我们介绍了如何为一个二维向量赋予绝对位置信息：旋转一定的角度即可。但我们知道词向量的维度一般是几百甚至上千，如何将我们上述旋转的结论推广到多维呢？分而治之即可，我们把高维向量，两两一组，分别旋转。最终高维向量的旋转可表示成如下公式，可以认为左侧便是高维向量的旋转矩阵： 

远程衰减性

在此前的推导中，我们说过  可以是一个任意常量，我们不妨将其设为1，以便查看其性质。我们随机初始化两个向量q和k，将q固定在位置0上，k的位置从0开始逐步变大，依次计算q和k之间的内积。我们发现随着q和k的相对距离的增加，它们之间的内积分数呈现出一定的震荡特性，缺乏了重要的远程衰减性，这并不是我们希望的。

借鉴Sinusoidal位置编码，我们可以将每个分组的  设为不同的常量，从而引入远程衰减的性质。这里作者直接沿用了Sinusoidal位置编码的设置，  。则我们可以将高维向量的旋转矩阵更新为如下

上式中的旋转矩阵十分稀疏，为了节省算力，可以以下面的方式等效实现：

‍

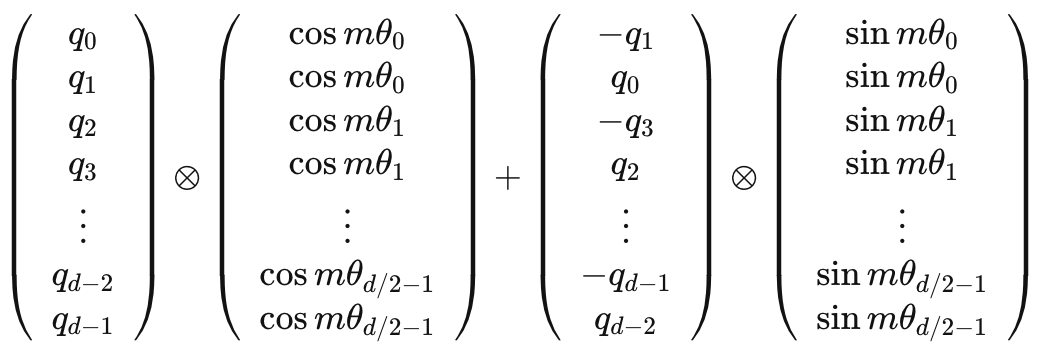
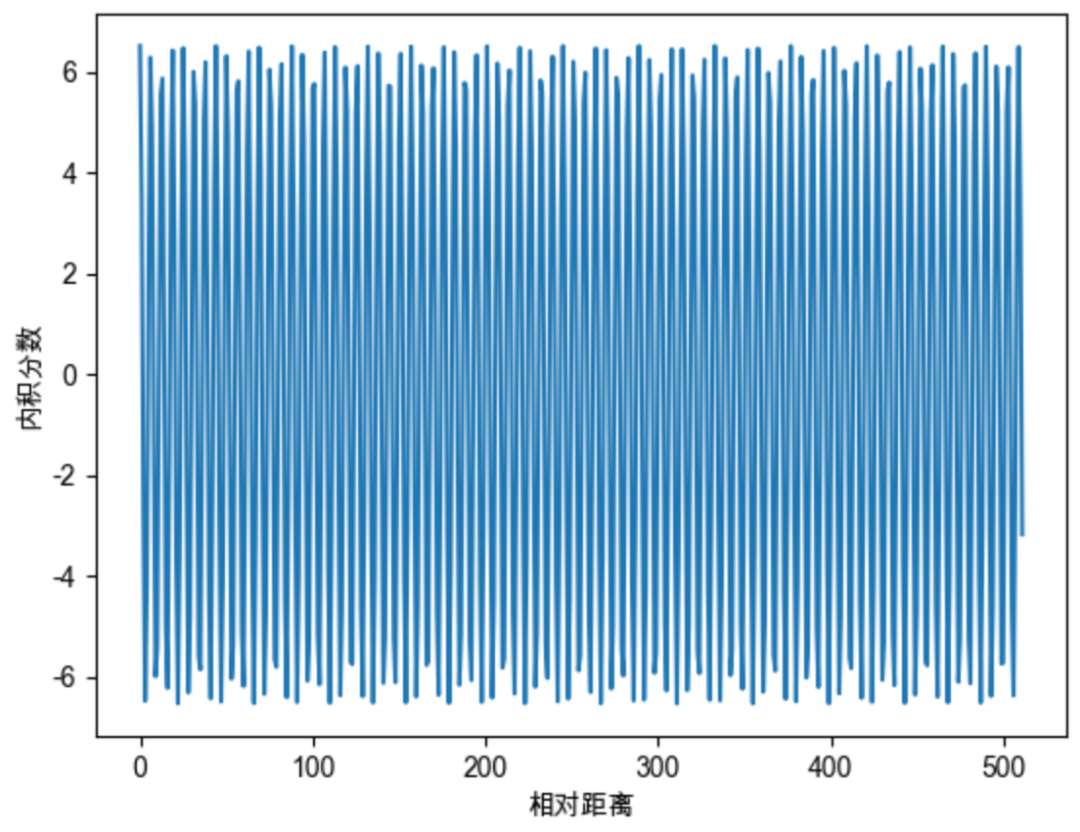
我们继续随机初始化两个向量q和k，将q固定在位置0上，k的位置从0开始逐步变大，依次计算q和k之间的内积。我们发现随着q和k的相对距离的增加，它们之间的内积分数呈现出远程衰减的性质，这正是我们希望的。

‍‍‍‍‍

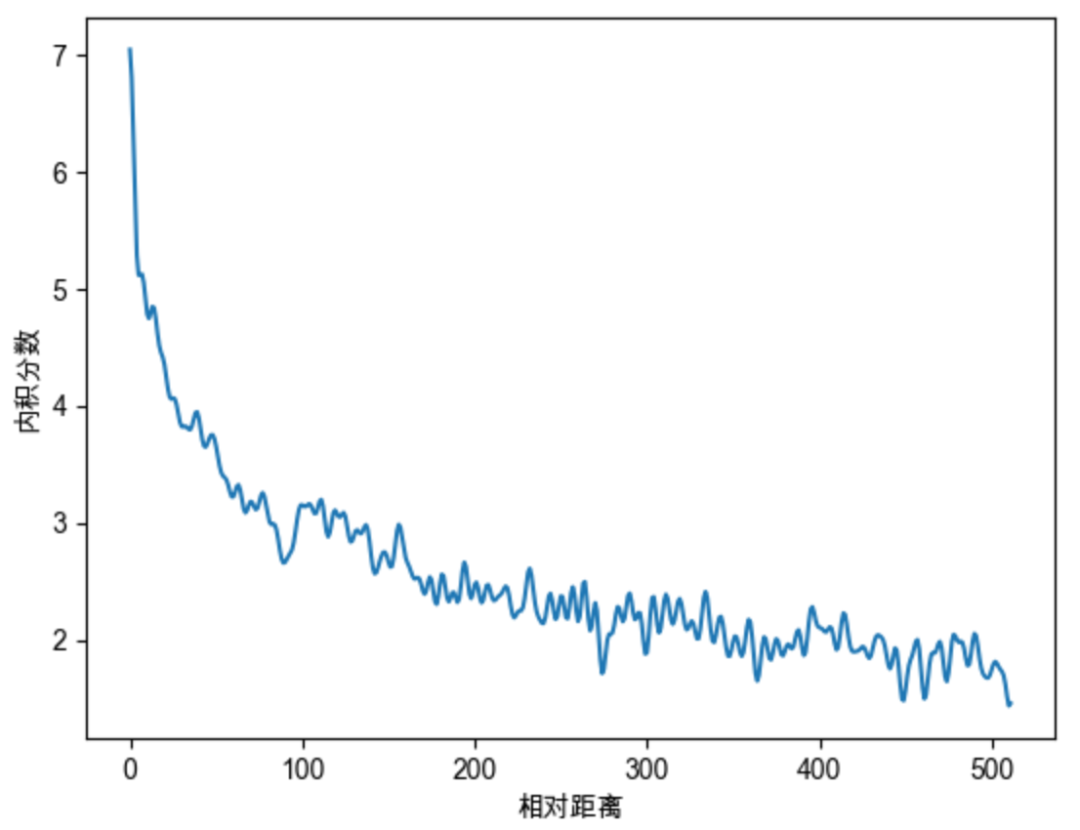
在原始的RoPE中，沿用了Si‍‍nusoidal位置编码的设置，令  ，但  一定要取  吗？我们继续深入探讨一下  中base的取值的影响。依然结合图像来进行说明，此次我们初始化两个全一向量q和k（为了让图像显得不那么杂乱‍‍），将q固定在位置0上，k的位置从0开始逐步变大，依次计算q和k之间的内积。当我们将base取不同的值的时候，q和k的内积随着相对位置变化趋势如下图。‍

‍ ‍ ‍ ‍

‍‍‍‍‍‍‍‍‍‍‍‍

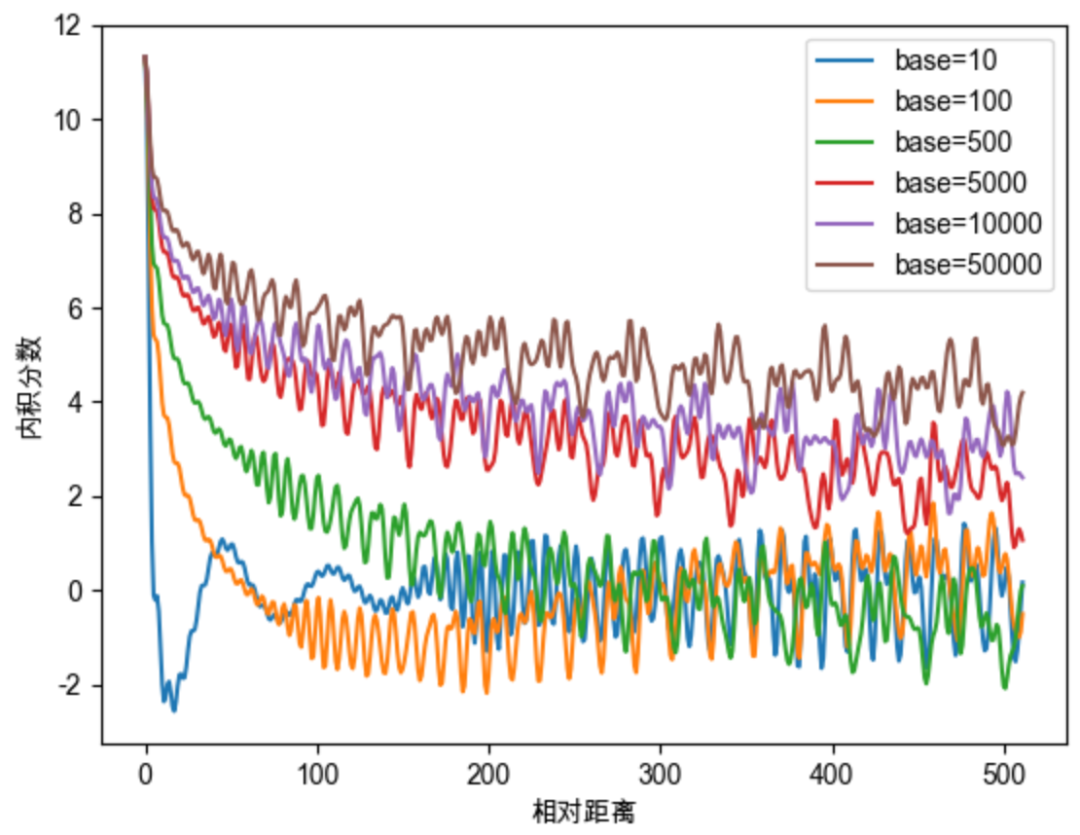
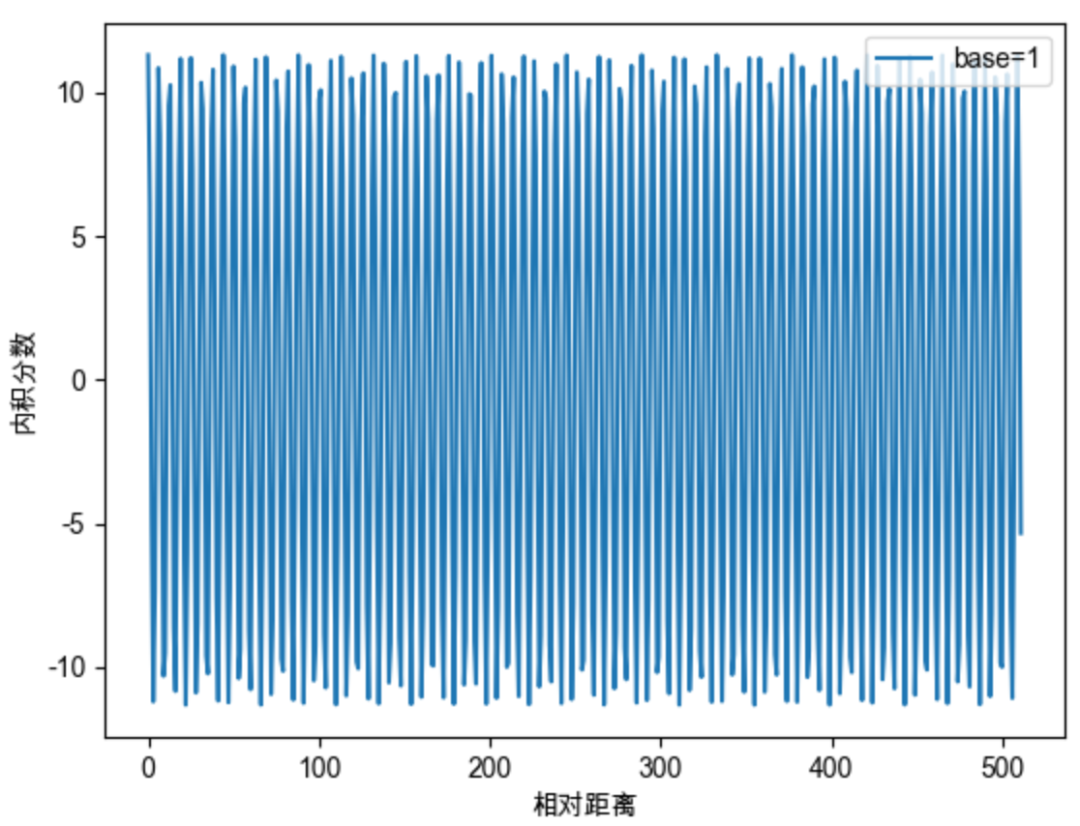
‍‍如上图我们可以总结得到一些规律，base的不同取值会影响注意力远程衰减的程度。当base大于500时，随着base的提升，远程衰减的程度会逐渐削弱。但太小的base也会破坏注意力远程衰减的性质，例如base=10或100时，注意力分数不再随着相对位置的增大呈现出震荡下降的趋势。更极端的情况下，当base=1时，其实也就是上面我们提到的，将所有  都设为1的情况，将完全失去远程衰减特性，如下图所示。

‍‍‍‍‍‍‍‍‍‍‍‍

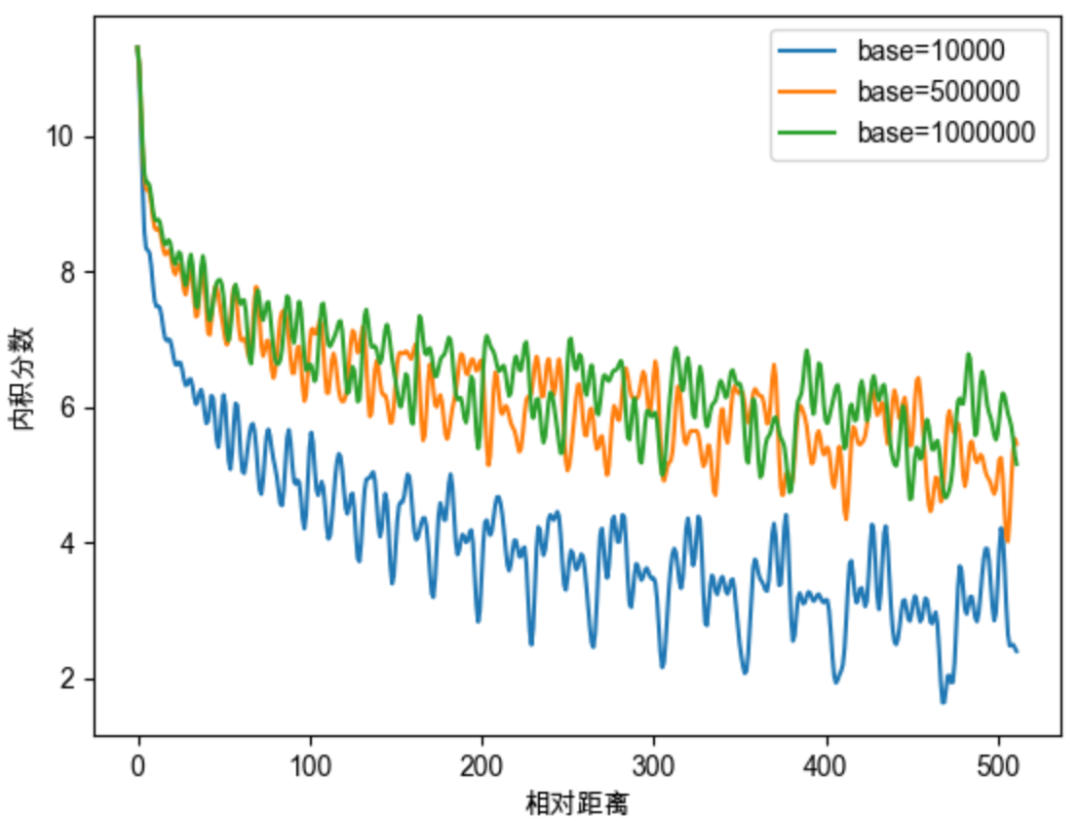
对于base的性质的研究，与大模型的长度外推息息相关，如NTK-Aware Scaled RoPE、NTK-by-parts、Dynamic NTK等长度外推方法，本质上都是通过改变base，从而影响每个位置对应的旋转角度，进而影响模型的位置编码信息，最终达到长度外推的目的。目前大多长度外推工作都是通过放大base以提升模型的输入长度，例如Code LLaMA将base设为1000000，LLaMA2 Long设为500000，但更大的base也将会使得注意力远程衰减的性质变弱，改变模型的注意力分布，导致模型的输出质量下降。如下图所示。

‍‍

在本文中，我们暂且不对长度外推工作展开介绍，后续我们将专门写一篇文章分享各种主流的长度外推方法。

05

结语

RoPE位置编码，以向量旋转这种简单巧妙的方式，实现了绝对位置编码，并且具备相对位置编码的能力。RoPE目前广泛应用于各种大模型，包括但不限于Llama、Baichuan、ChatGLM、Qwen等。基于RoPE的长度外推工作不断涌现，并且获得了非常优秀的效果。如果当前你需要研究大模型的长度外推工作，那么弄清楚RoPE的底层原理则为一门必修课。

后续我们也将继续以图解的方式，对现有的长度外推工作进行分享介绍。

---

备注：昵称-学校/公司-方向/会议(eg.ACL)，进入技术/投稿群

id：DLNLPer，记得备注呦