NLP笔记：n-grams语言模型

n-gram语言模型是自然语言处理中一种简单而常用的统计语言模型。它用于估计文本中的语言概率和生成文本。n-gram模型基于一个假设：一个词的出现只依赖于前面的n-1个词。因此，n-gram模型将文本中的词序列表示为连续的n个词的序列。

具体来说，n-gram模型有以下特点和步骤：

1. n的选择： 首先，需要选择n的值，这决定了n-gram模型中考虑的上下文的长度。常见的选择包括unigram（1-gram，单个词）、bigram（2-gram，两个连续的词）、trigram（3-gram，三个连续的词）等。

2. 建立n-gram模型： 针对给定的文本语料库，统计每个n-gram序列的出现频率，并计算条件概率。这些概率用于估计下一个词在给定前面的n-1个词的情况下出现的概率。

3. 计算概率： 对于一个给定的文本序列，可以使用n-gram模型来计算文本的概率。这通常涉及将文本划分为n-gram序列，然后将各个n-gram的概率相乘，得到整个文本的概率。

4. 生成文本： 可以使用n-gram模型来生成文本，从一个起始词开始，根据条件概率选择下一个词，并不断生成下一个词，直到生成所需长度的文本或遇到终止符号。

5. 平滑技术： 在实际应用中，为了解决数据稀疏性和零概率问题，常常使用平滑技术（如Laplace平滑、Add-One平滑）来调整概率估计。

6. 应用领域： n-gram语言模型广泛用于文本生成、文本分类、机器翻译、拼写纠正、语音识别等自然语言处理任务中。

需要注意的是，n-gram语言模型具有局限性，主要在于它不能捕捉长距离的依赖关系，因为它只考虑n个连续词的上下文。在实际应用中，更复杂的神经网络语言模型（如Transformer模型）通常能够更好地建模语言的复杂结构和长距离依赖。但n-gram模型仍然在一些简单任务和资源受限的环境中有其用武之地。

概率模型

• 随机变量

• 概率

• 推断

• 条件独立性（假设单词与单词之间没有关系）

  • $P(A,B)=P(A)P(B)$

  • $P(A)=\sum P(A|B_i)P(B_i)$

• 极大似然估计→对数似然估计

  • 参数估计的方法之一

  • 应用：

    • （已知序列，推测分布）已知某个随机样本满足某种概率分布，但是其中具体的参数不清楚，参数估计就是通过若干次试验，观察其结果，利用结果推出概率分布

    • 基于某个已知分布推测序列的下一个值

  • 似然估计提供了一种区分概率的方法，也是一种在所有可能性中选择单个最佳概率的策略

语言模型的概念

• 不同句子的语言模型概率

  • 计算不同序列的联合分布概率，概率越低说明约不符合自然语言

• 计算语言序列的正确概率

• 判断语言序列是否是正常语句

• 已知若干个词，预判下一个词

语言模型的用途：语音识别、上写文敏感的拼写检查、手写识别、OCR、机器翻译……

计算一个句子或一系列单词的概率

给定单词序列 W = { w 1 , w 2 , … , w n } W=\{w_1,w_2,\ldots,w_n\} W={w1​,w2​,…,wn​}，计算联合概率$P(W)=P(w_1,w_2,\dots ,w_n)$

概率链式规则

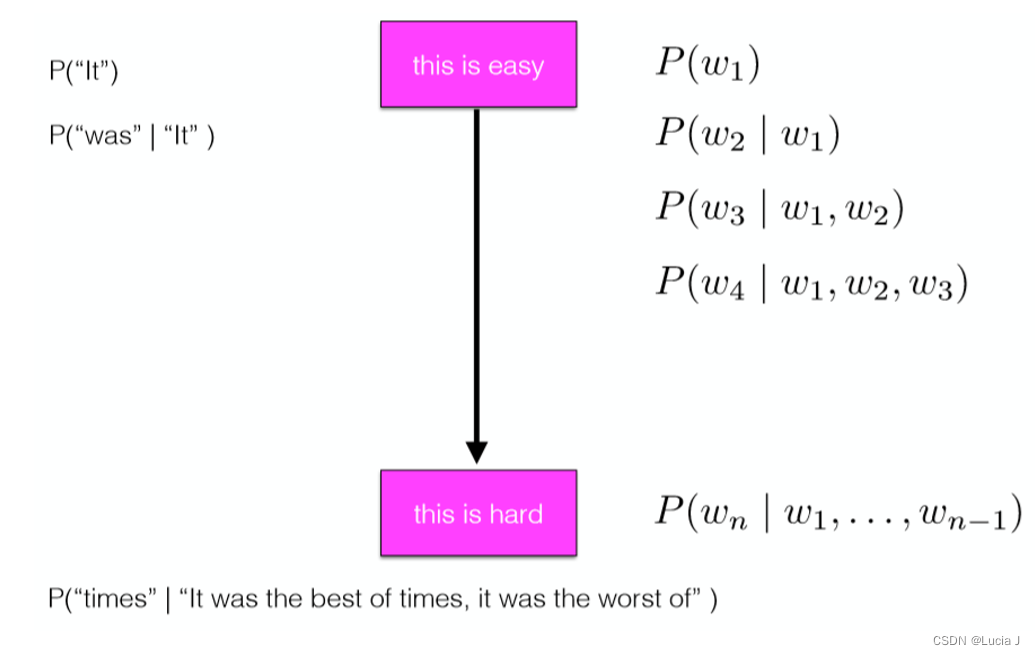
将联合概率分布转化为条件概率分布的连乘

$P(W)={\prod }_{t=1}^{n}P(w_t|w_0{w}_1\dots w_{t-1})$

马尔科夫假设

• $P(W)=\prod P(w_i)$：Unigram 一元语言模型

• $P(W)=\prod P(w_i|w_0,w_1,\dots ,w_{i-1})=\prod P(w_i|w_{i-1})$：Bigram 二元语言模型

• $P(W)=\prod P(w_i|w_0,w_1,\dots ,w_{i-1})=\prod P(w_i|w_{i-2},w_{i-1})$：Trigram 三元语言模型

• ……

n-gram语言模型

一个不充分的语言模型，因为语言具有远距离依赖性

$P(w_n|w_{n-N+1}^{n-1})=\frac{C(w_{n-N+1}^{n-1}{w}_n)}{C(w_{n-N+1}^{n-1})}$

我们在面临实际问题时，如何选择依赖词的个数，即n：

• 更大的n：对下一个词出现的约束信息更多，具有更大的辨别力；

• 更小的n：在训练语料库中出现的次数更多，具有更可靠的统计信息

• 理论上，n越大越好，经验上，trigram用的最多，尽管如此，原则上，能用bigram解决，绝不使用trigram

• n>=4时数据稀疏和计算代价又变得显著起来，实际工程中几乎不使用

• 深度学习带了一种递归神经网络语言模型（RNN Language Model），理论上可以记忆无限个单词，可以看作“无穷元语法”（∞-gram）

语言模型评估

外部评估

• 直接应用于下游任务，观察精度→直接针对下游应用进行优化微调

  • 更高的任务准确性→更好的模型

  • 大语言模型不需要微调（已经优化过了）

内部评估

• 训练：在合适的训练语料库上训练参数

  • 假设：观察到的句子~好句子

• 测试：在不同的、unseen的语料库上测试

  • 如果语言模型将更高的概率分配给测试集中的句子，则更好

  • 注意：训练集和测试集语料库不能有交集！！

• 评估指标：困惑度

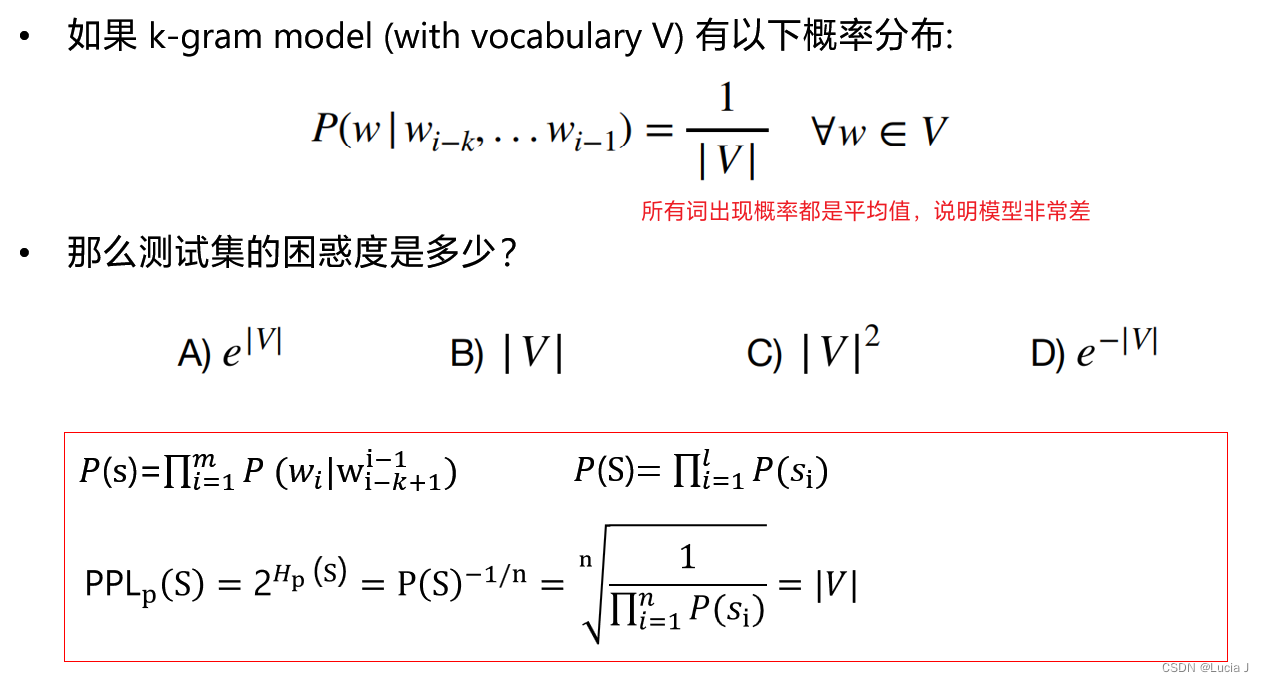
困惑度（PPL）

定义

PPL越低越好：困惑度最小→最大化语料库的概率

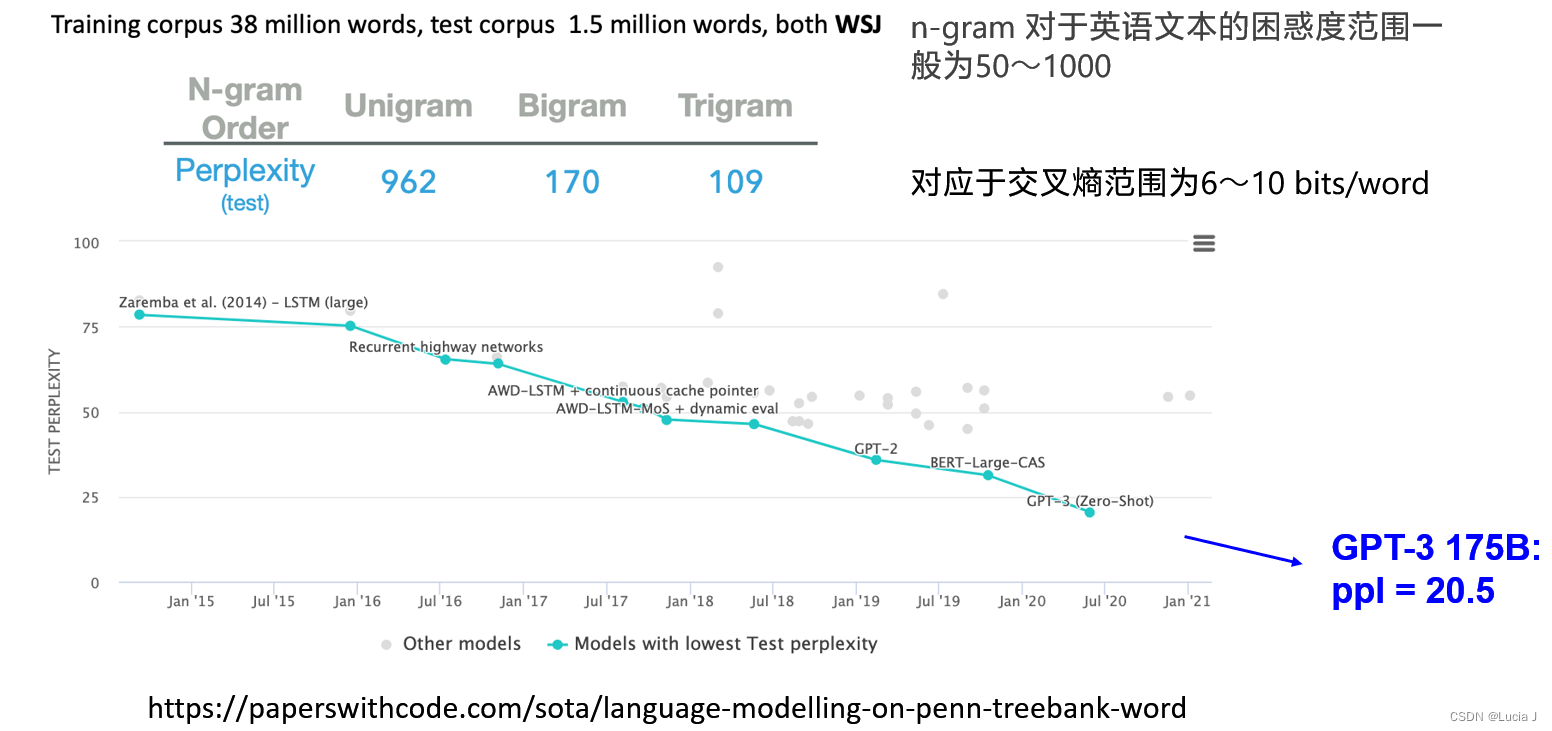
n-grams生成存在的问题

• 并非测试集中所有n元语法都会在训练数据中都出现过

• 测试语料库可能有一些在我们的模型中的概率为零，导致PPL分母为0，没有意义

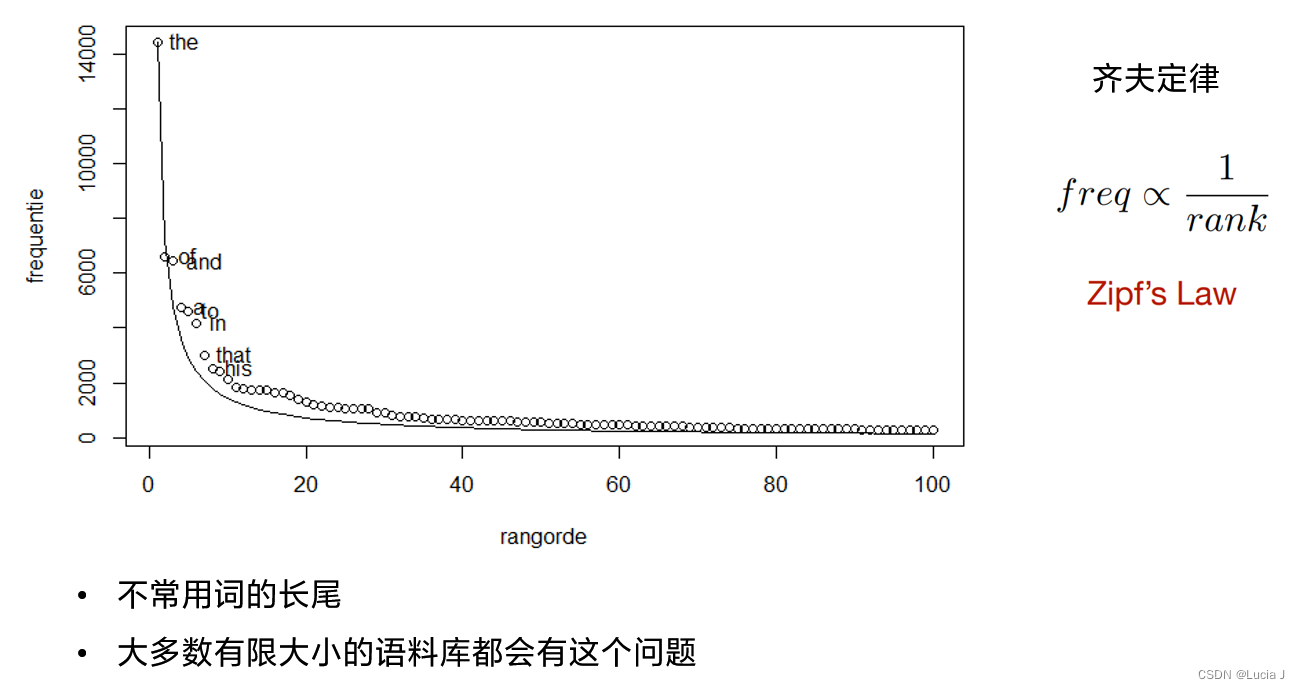
齐夫定律（稀疏性）

在自然语言的语料库里，一个单词出现的频率与它在频率表里的排名成反比。所以，频率最高的单词出现的频率大约是出现频率第二位的单词的2倍，而出现频率第二位的单词则是出现频率第四位的单词的2倍。

平滑机制

简介

• 基本思想：调整最大似然估计的概率值，使零概率增值，使非零概率下调，“劫富济贫”，消除零概率，改进模型的整体正确率

• 基本目标：测试样本的语言模型困惑度越小越好

• 基本约束：$\sum P(w_i|w_1,w_2,\dots ,w_n)=1$

拉普拉斯平滑

基本思想：每一种情况出现的次数加1或者一个极小值 α 到所有计数并重新规范化

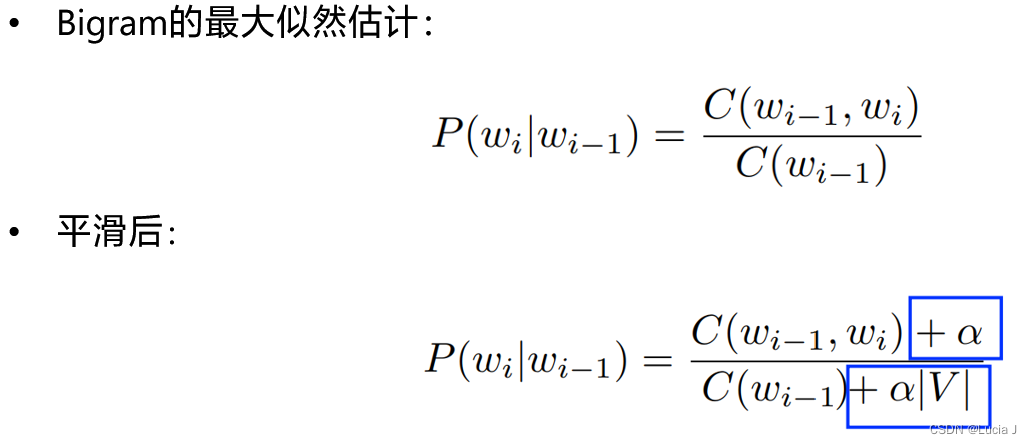
其中$|V|$表示语料库中单词总数

减值法/折扣法

基本思想：修改训练样本中事件的实际计数，使样本中(实际出现的)不同事件的概率之和小于1，剩余的概率量分配给未见概率

Good-Turing估计

增加了出现0次的单词的概率

当某一事件在样本中出现的频率大于阈值K (通常取K 为0 或1)时，运用最大似然估计的减值法来估计其概率，否则，使用低阶的，即(n-1)gram 的概率替代n-gram 概率，而这种替代需受归一化因子的作用

P k a t z ( w i ∣ w i − 1 ) = { d r C ( w i − 1 w i ) C ( w i − 1 ) C ( w i − 1 w i ) = r > 0 α ( w i − 1 ) P M L ( w i ) C ( w i − 1 w i ) = 0 P_{katz}(w_i|w_{i-1})=

$$\begin{cases} d_r\frac{C(w_{i-1}w_i)}{C(w_{i-1})}&C(w_{i-1}w_i)=r>0\\ \alpha(w_{i-1})P_{ML}(w_i)&C(w_{i-1}w_{i})=0 \end{cases}$$ Pkatz​(wi​∣wi−1​)={dr​C(wi−1​)C(wi−1​wi​)​α(wi−1​)PML​(wi​)​C(wi−1​wi​)=r>0C(wi−1​wi​)=0​

Back-off ( 后备/后退 )方法

绝对减值法( Absolute discounting )

线性减值法( Linear discounting )

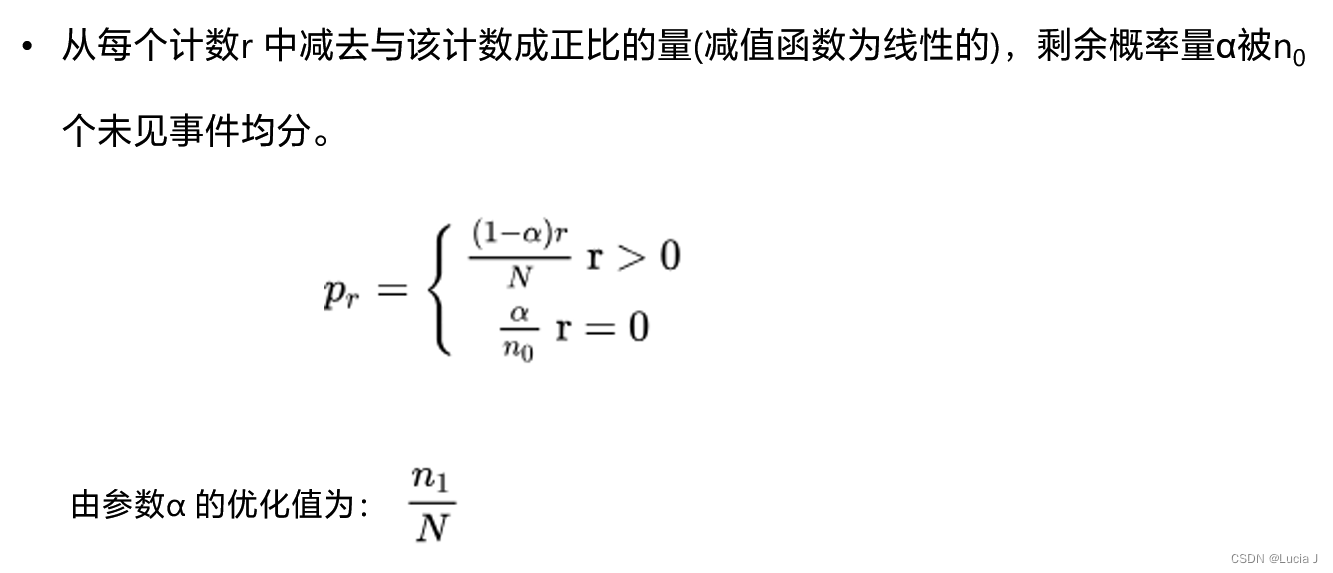
删除插值法