排序算法之优先级队列与堆排序_优先级排序算法

原文链接：点击打开链接

 

在很多应用中，我们通常需要按照优先级情况对待处理对象进行处理，比如首先处理优先级最高的对象，然后处理次高的对象。最简单的一个例子就是，在手机上玩游戏的时候，如果有来电，那么系统应该优先处理打进来的电话。

在这种情况下，我们的数据结构应该提供两个最基本的操作，一个是返回最高优先级对象，一个是添加新的对象。这种数据结构就是优先级队列(Priority Queue) 。

本文首先介绍优先级队列的定义，有序和无序数组以及堆数据结构实现优先级队列，最后介绍了基于优先级队列的堆排序(Heap Sort)

一 定义

优先级队列和通常的栈和队列一样，只不过里面的每一个元素都有一个”优先级”，在处理的时候，首先处理优先级最高的。如果两个元素具有相同的优先级，则按照他们插入到队列中的先后顺序处理。

优先级队列可以通过链表，数组，堆或者其他数据结构实现。

二 实现

数组

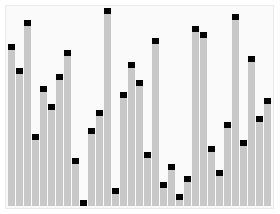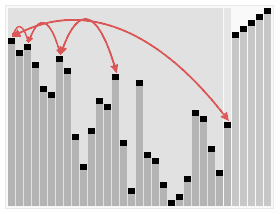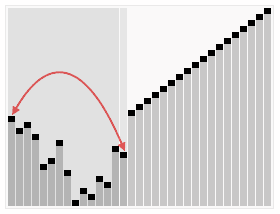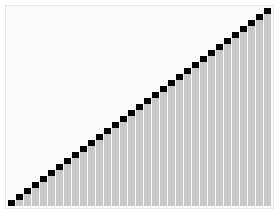
最简单的优先级队列可以通过有序或者无序数组来实现，当要获取最大值的时候，对数组进行查找返回即可。代码实现起来也比较简单，这里就不列出来了。

如上图：

· 如果使用无序数组，那么每一次插入的时候，直接在数组末尾插入即可，时间复杂度为O(1)，但是如果要获取最大值，或者最小值返回的话，则需要进行查找，这时时间复杂度为O(n)。

· 如果使用有序数组，那么每一次插入的时候，通过插入排序将元素放到正确的位置，时间复杂度为O(n)，但是如果要获取最大值的话，由于元阿苏已经有序，直接返回数组末尾的 元素即可，所以时间复杂度为O(1).

所以采用普通的数组或者链表实现，无法使得插入和排序都达到比较好的时间复杂度。所以我们需要采用新的数据结构来实现。下面就开始介绍如何采用二叉堆(binary heap)来实现优先级队列

二叉堆

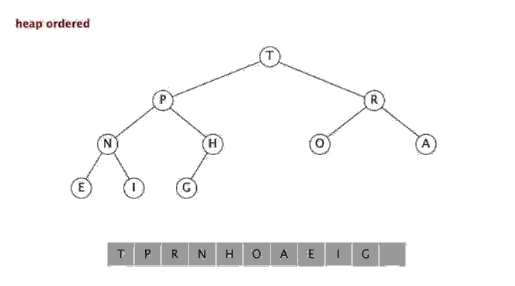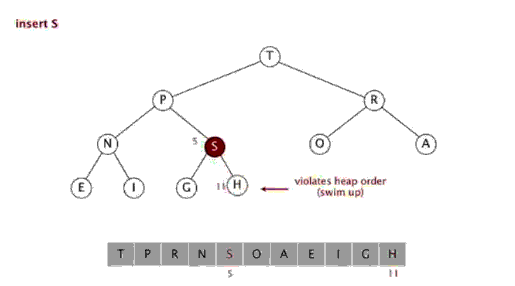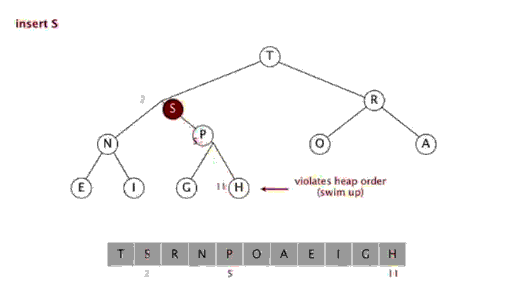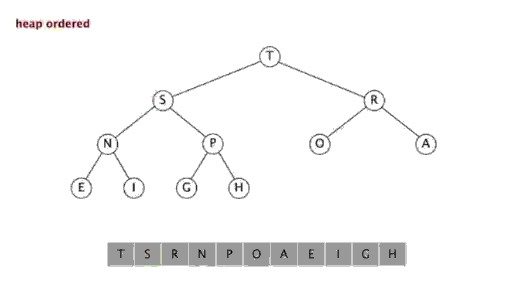
二叉堆是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。 有了这一性质，那么二叉堆上最大值就是根节点了。

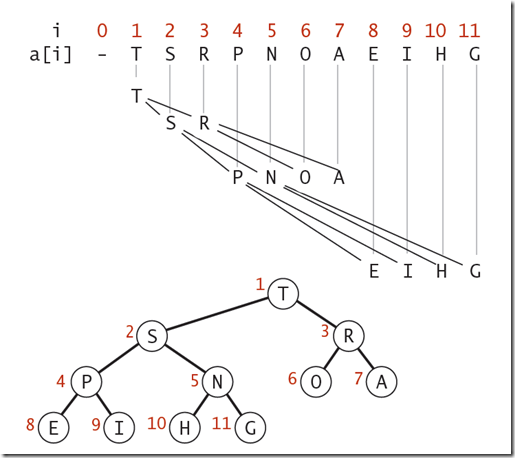
二叉堆的表现形式：我们可以使用数组的索引来表示元素在二叉堆中的位置。

从二叉堆中，我们可以得出：

· 元素k的父节点所在的位置为[k/2]

· 元素k的子节点所在的位置为2k和2k+1

跟据以上规则，我们可以使用二维数组的索引来表示二叉堆。通过二叉堆，我们可以实现插入和删除最大值都达到O(nlogn)的时间复杂度。

对于堆来说，最大元素已经位于根节点，那么删除操作就是移除并返回根节点元素，这时候二叉堆就需要重新排列；当插入新的元素的时候，也需要重新排列二叉堆以满足二叉堆的定义。现在就来看这两种操作。

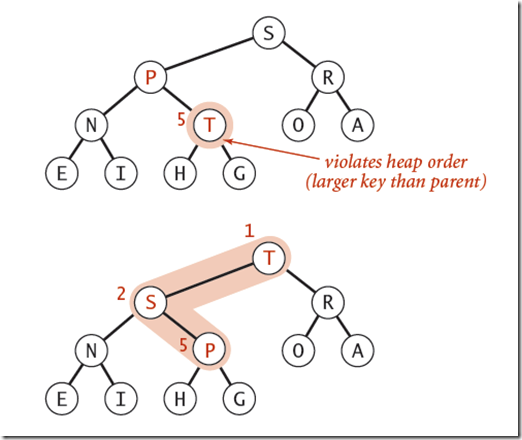
从下至上的重新建堆操作: 如果一个节点的值大于其父节点的值，那么该节点就需要上移，一直到满足该节点大于其两个子节点，而小于其根节点为止，从而达到使整个堆实现二叉堆的要求。

由上图可以看到，我们只需要将该元素k和其父元素k/2进行比较，如果比父元素大，则交换，然后迭代，一直到比父元素小为止。

private static void Swim(int k)
{
    //如果元素比其父元素大，则交换
    while (k > 1 && pq[k].CompareTo(pq[k / 2]) > 0)
    {
        Swap(pq, k, k / 2);
        k = k / 2;
    }
}Swim(int k)
{
    //如果元素比其父元素大，则交换
    while (k > 1 && pq[k].CompareTo(pq[k / 2]) > 0)
    {
        Swap(pq, k, k / 2);
        k = k / 2;
    }
}

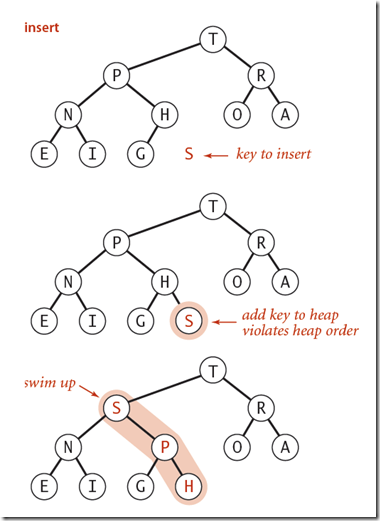
这样，往堆中插入新元素的操作变成了，将该元素从下往上重新建堆操作：

代码实现如下：

public static void Insert(T s)
{
    //将元素添加到数组末尾
    pq[++N] = s;
    //然后让该元素从下至上重建堆
    Swim(N);
}Insert(T s)
{
    //将元素添加到数组末尾
    pq[++N] = s;
    //然后让该元素从下至上重建堆
    Swim(N);
}

动画如下：

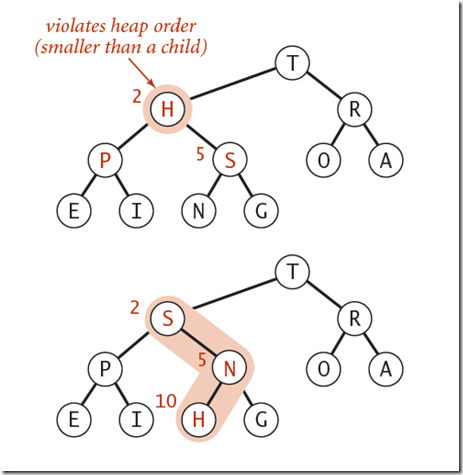
由上至下的重新建堆操作：当某一节点比其子节点要小的时候，就违反了二叉堆的定义，需要和其子节点进行交换以重新建堆，直到该节点都大于其子节点为止：

代码实现如下:

private static void Sink(int k)
{
    while (2 * k < N)
    {
        int j = 2 * k;
        //去左右子节点中，稍大的那个元素做比较
        if (pq[j].CompareTo(pq[j + 1]) < 0) j++;
        //如果父节点比这个较大的元素还大，表示满足要求，退出
        if (pq[k].CompareTo(pq[j]) > 0) break;
        //否则，与子节点进行交换
        Swap(pq, k, j);
        k = j;
    }
}Sink(int k)
{
    while (2 * k < N)
    {
        int j = 2 * k;
        //去左右子节点中，稍大的那个元素做比较
        if (pq[j].CompareTo(pq[j + 1]) < 0) j++;
        //如果父节点比这个较大的元素还大，表示满足要求，退出
        if (pq[k].CompareTo(pq[j]) > 0) break;
        //否则，与子节点进行交换
        Swap(pq, k, j);
        k = j;
    }
}

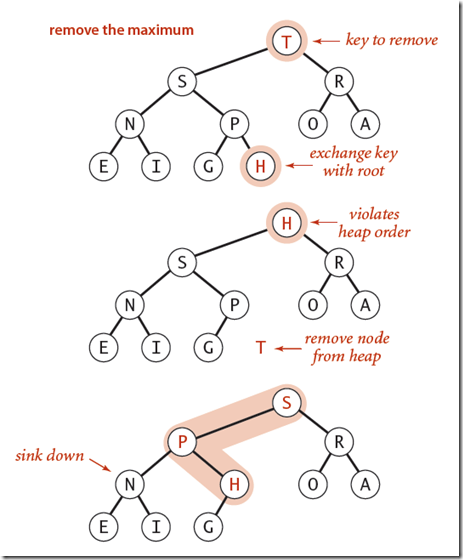
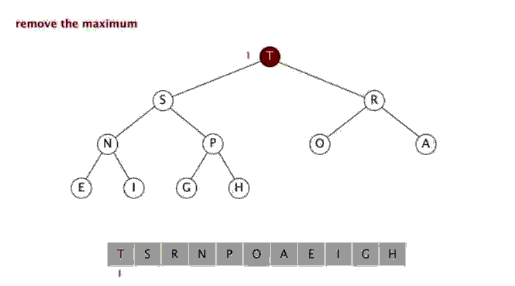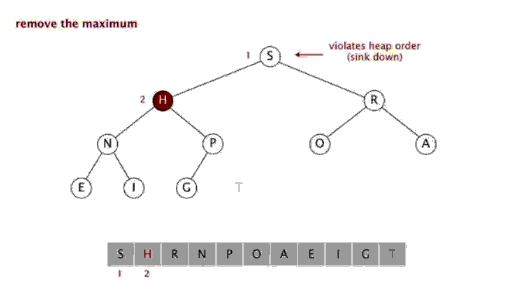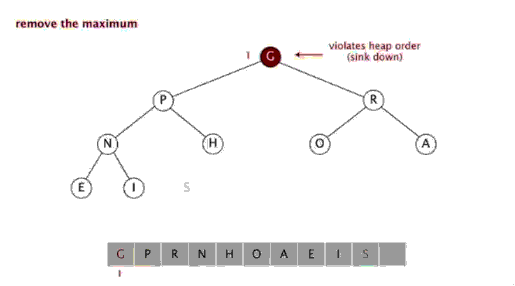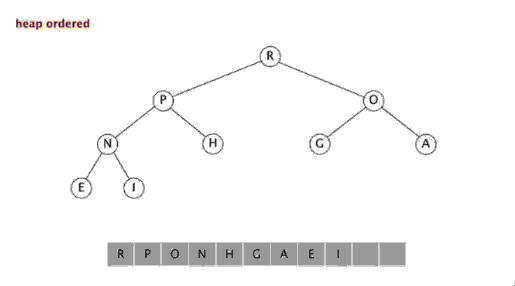
这样，移除并返回最大元素操作DelMax可以变为：

1. 移除二叉堆根节点元素，并返回

2. 将数组中最后一个元素放到根节点位置

3. 然后对新的根节点元素进行Sink操作，直到满足二叉堆要求。

移除最大值并返回的操作如下图所示：

以上操作的实现如下：

public static T DelMax()
{
    //根元素从1开始，0不存放值
    T max = pq[1];
    //将最后一个元素和根节点元素进行交换
    Swap(pq, 1, N--);
    //对根节点从上至下重新建堆
    Sink(1);
    //将最后一个元素置为空
    pq[N + 1] = default(T);
    return max;
}T DelMax()
{
    //根元素从1开始，0不存放值
    T max = pq[1];
    //将最后一个元素和根节点元素进行交换
    Swap(pq, 1, N--);
    //对根节点从上至下重新建堆
    Sink(1);
    //将最后一个元素置为空
    pq[N + 1] = default(T);
    return max;
}

动画如下：

三 堆排序

概念

运用二叉堆的性质，可以利用它来进行一种就地排序，该排序的步骤为：

1. 使用序列的所有元素，创建一个最大堆。

2. 然后重复删除最大元素。

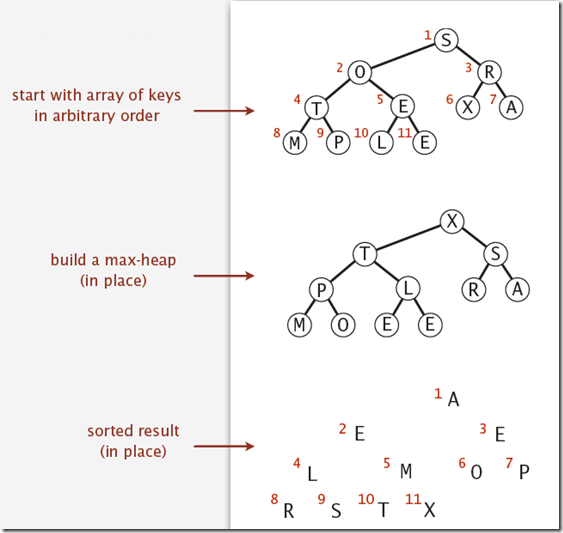
如下图，以对S O R T E X A M P L E 排序为例，首先本地构造一个最大堆，即对节点进行Sink操作，使其符合二叉堆的性质。

然后再重复删除根节点，也就是最大的元素，操作方法与之前的二叉堆的删除元素类似。

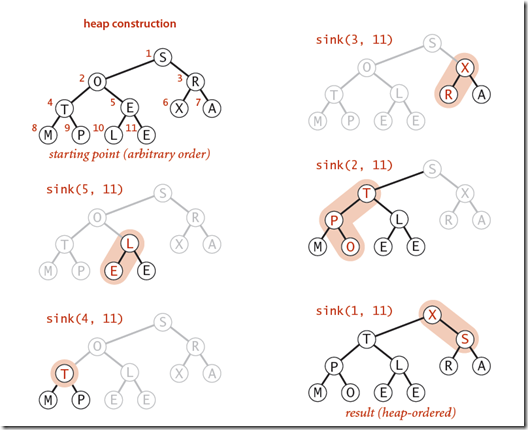
创建最大二叉堆：

使用至下而上的方法创建二叉堆的方法为，分别对叶子结点的上一级节点以重上之下的方式重建堆。

代码如下：

for (int k = N / 2; k >= 1; k--)
{
    Sink(pq, k, N);
}(int k = N / 2; k >= 1; k--)
{
    Sink(pq, k, N);
}

排序

利用二叉堆排序其实就是循环移除顶部元素到数组末尾，然后利用Sink重建堆的操作。如下图，实现代码如下：

while (N > 1)
{
    Swap(pq, 1, N--);
    Sink(pq, 1, N);
}(N > 1)
{
    Swap(pq, 1, N--);
    Sink(pq, 1, N);
}

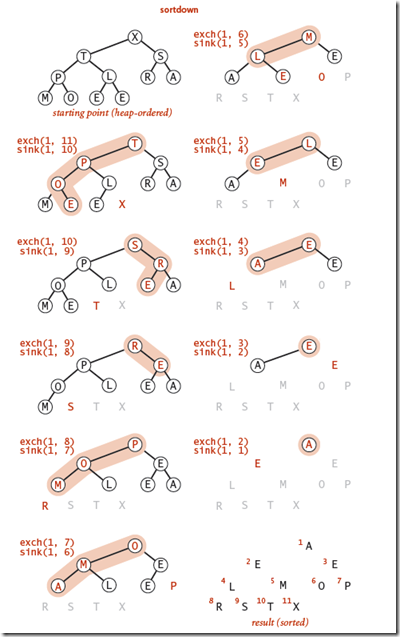
堆排序的动画如下：

分析

1. 在构建最大堆的时候，最多需要2N次比较和交换

2. 堆排序最多需要2NlgN次比较和交换操作

优点：堆排序最显著的优点是，他是就地排序，并且其最坏情况下时间复杂度为NlogN。经典的合并排序不是就地排序，它需要线性长度的额外空间，而快速排序其最坏时间复杂度为N2

缺点：堆排序对时间和空间都进行了优化，但是：

1. 其内部循环要比快速排序要长。

2. 并且其操作在N和N/2之间进行比较和交换，当数组长度比较大的时候，对CPU缓存利用效率比较低。

3. 非稳定性排序。

四 排序算法的小结

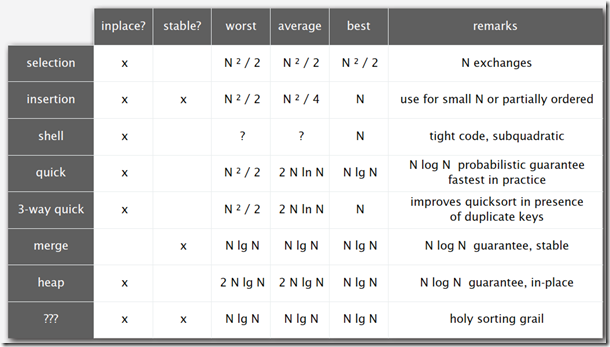
本文及前面文章介绍了选择排序，插入排序，希尔排序，合并排序，快速排序以及本文介绍的堆排序。各排序的稳定性，平均，最坏，最好的时间复杂度如下表：

可以看到，不同的排序方法有不同的特征，有的速度快，但是不稳定，有的稳定，但是不是就地排序，有的是就地排序，但是最坏情况下时间复杂度不好。那么有没有一种排序能够集合以上所有的需求呢?

五 结语

本文介绍了二叉堆，以及基于二叉堆的堆排序，他是一种就地的非稳定排序，其最好和平均时间复杂度和快速排序相当，但是最坏情况下的时间复杂度要优于快速排序。但是由于他对元素的操作通常在N和N/2之间进行，所以对于大的序列来说，两个操作数之间间隔比较远，对CPU缓存利用不太好，故速度没有快速排序快。

下文将开始介绍查找算法，并介绍二叉查找树。

C++完整代码：

#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
 
void adjust(int arr[], int len, int index)
{
	int left = 2 * index + 1;
	int right = 2 * index + 2;
	int maxIdx = index; //当前节点不是叶子节点
	if (left<len && arr[left] > arr[maxIdx]) maxIdx = left;
	if (right<len && arr[right] > arr[maxIdx]) maxIdx = right;  // maxIdx是3个数中最大数的下标
	if (maxIdx != index)                 // 如果maxIdx的值有更新
	{
		swap(arr[maxIdx], arr[index]);
		adjust(arr, len, maxIdx);       // 递归调整其他不满足堆性质的部分
	}
 
}
void heapSort(int arr[], int size)
{
	for (int i = size / 2 - 1; i >= 0; i--)  // 对每一个非叶结点进行堆调整,构建二叉堆
	{
		adjust(arr, size, i);
	}
	for (int i = size - 1; i >= 1; i--)
	{
		swap(arr[0], arr[i]);           // 将当前最大的放置到数组末尾
		adjust(arr, i, 0);              // 将未完成排序的部分继续进行堆排序
	}
}
 
int main()
{
	int array[8] = { 8, 1, 14, 3, 21, 5, 7, 10 };
	heapSort(array, 8);
	for (auto it : array)
	{
		cout << it << " "  ;
	}
	cout << endl;
	getchar();
	return 0;
}