C/C++ 动态规划 算法_c++动态规划算法

动态规划算法，以最小的消耗解题！

以一个走楼梯为例子展开。

假设有一个三级台阶，我们一次可以走一步，或者一次走两步，那么由此可知，一共有3中走法，如下图

当台阶数量少的时候，确实很容易解出来；那如果台阶数量是5呢，是10呢，是20呢。。。

这样复杂程度就蹭蹭蹭的放上涨了，这时就很那靠脑力算出来，所以得靠程序算法去求解。

可以使用递归的思维去求解！

从上往下分析问题，大问题可以分解为子问题，子问题中还有更小的子问题

比如总共有 5 级台阶,求有多少种走法；由于一次可以走两级台阶，也可以走一级台阶，所以我们可以分成两个情况

• 最后一次走了两级台阶，问题变成了“走上一个 3 级台阶，有多少种走法？”
• 最后一步走了一级台阶，问题变成了“走一个 4 级台阶，有多少种走法？”

我们将求 n 级台阶的共有多少种走法用 f(n) 来表示，则 f(n) = f(n-1) + f(n-2);

由上可得

f(5) = f(4) + f(3);

f(4) = f(3) + f(2);

f(3) = f(2) + f(1);

边界情况分析

走一步台阶时，只有一种走法，所以 f(1)=1

走两步台阶时，有两种走法，直接走 2 个台阶，分两次每次走 1 个台阶，所以 f(2)=2

走两个台阶以上可以分解成上面的情况

所以使用递归实现代码如下：

int WalkCount(int n) {
 
	if (n <= 0) return 0;
 
	if (1 == n) {	// 一级台阶，一种走法
		return 1;
 
	} else if (2 == n) {
 
		return 2;	// 二级台阶，二种走法
	}
 
	// f(n) = f(n-1) + f(n-2);
	return WalkCount(n - 1) + WalkCount(n - 2);
}

编写main方法进行测试：

int main(void) {
 
	int n = 0;
 
	printf("请输入台阶的级数：");
	scanf_s("%d", &n);
 
	for (int i = 0; i <= n; i++) {
		printf("走 %d 级台阶共有 %d 当中走法!\n", i, WalkCount(i));
	}	
 
	return 0;
}

编译输出：

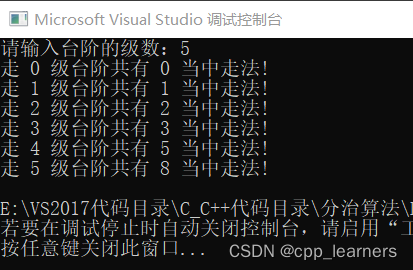
 确实可以计算出来，但这种方式有种问题！

细心的朋友是否会注意到，上面的代码中存在很多重复的计算？

比如: f(5) = f(4) + f(3)

计算分成两个分支：

f(4) = f(3)+f(2) = f(2) + f(1) + f(2);

f(3) = f(2) + f(1);

上面阴影的部分就是重复计算的一部分！

有没有办法避免重复计算的部分？

其实我们可以从下向上分析推断问题。

f(1) = 1 f(2) = 2

f(3) = f(1) + f(2) = 3

f(4) = f(3) + f(2) = 3 + 2 = 5

f(5) = f(4) + f(3) = 5 + 3 = 8

依次类推 ...

我们可以不使用递归，从下往上进行分析推断问题，可以定义一个数组将之前计算好的数据保存下来，等到上面需要使用时，直接提取出来计算即可！

实现代码如下：

long long WalkCount2(int n) {
 
	if (0 >= n) return 0;
	if (1 == n) return 1;
	if (2 == n) return 2;
 
	long long *arr = (long long *)malloc(sizeof(long long)*(n + 1));
	memset(arr, 0, sizeof(n)*(n + 1));
 
	*(arr + 0) = 0;		// arr[0] = 0;
	*(arr + 1) = 1;		// arr[1] = 1;
	*(arr + 2) = 2;		// arr[2] = 2;
 
	for (int i = 3; i <= n; i++) {
		// arr[3] = arr[i-1] + arr[i-2];
		*(arr + i) = *(arr + (i-1)) + *(arr + (i-2));
	}
 
	long long ret = *(arr + n);
	
	free((void *)arr);
	return ret;
}

使用以下代码进行测试：

int main(void) {
 
	int n = 0;
 
	printf("请输入台阶的级数：");
	scanf_s("%d", &n);
 
	for (int i = 0; i <= n; i++) {
		printf("走 %d 级台阶共有 %lld 当中走法!\n", i, WalkCount2(i));
	}
	
	return 0;
}

运行截图：

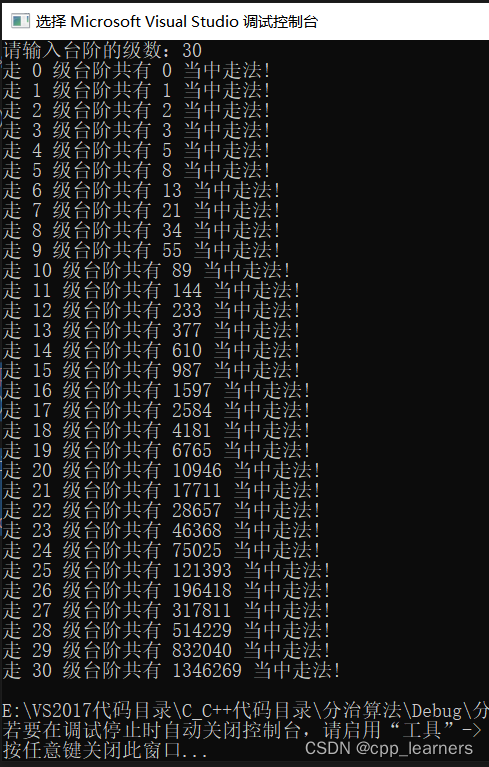
可以很快速的计算出来。

还可以计算更大的数据，例如1000次，只要计算的数据long long类型可以存储，那么都是可以很快的计算出来，但如果是递归，则需要花费很多时间，因为他在做重复的计算工作！

---

动态规划算法实现就是类似这样；当然并不是所有的递归都可以使用动态规划算法来实现，得要有重复计算的才可以！