【atcoder】abc312~abc321题解_atcoder abc语法好题

UNIQUE VISION Programming Contest 2023 Summer(AtCoder Beginner Contest 312)

A

把信息存进去然后找就行。

B

枚举右上角，然后模拟判断即可。

C

二分这个 $X$ ，然后判断即可。

D

典型的括号类的 $dp$ 。$d{p}_{i,j}$ 表示前i个字符，左-右= $j$ 的方案数，答案为$d{p}_{n,0}$。若si=$($ 或者 $)$ 显然对于任意 $d{p}_{i,j}$ 是固定的，故直接继承上一层即可。若为 $?$，则分别加上是 $($ 的方案和 $)$ 的方案即可。

E

用一个三维数组记录一下每个位置是哪个块存下标。相邻的两个位置显然满足其中一维的差为 $1$ 且仅有一维。那么枚举 $(i,j,k)$，对其相邻的块查看是否有块的存在并且不是他自己的块，如果是就把i的答案里记录一下，相邻的块的所属块也记录一下，用 $set$ 搞就行。

F

贪心。设物品1,2,3的数量分别为 $n1,n2,n3$ 。那么枚举使用 $0n3$ 个物品 $3$ 的情况下的最大快乐值。贪心的选，那么显然就是在选 $1$的是后要取大的，23同理也是。用 $num1,num2$ 记录一下 $12$ 的使用数量，如果当前的数量超标就抛弃一个小的。接下来不停的选物品 $2$，然后如果当前的这个物品 $3$ 还可以继续开物品 $2$ 就并且物品2还有没选的就不停的替换物品 $1$（如果比物品1大的话），最后把所有的情况取个 $max$ 即可。

G

可以发现 $(i,j,k)$ 的结构一定是如下的：

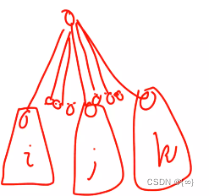
那么此时可以想到对于每一个 $u(1\le u\le n)$ 统计形式如上图的这样的三元对个数，加到 $ans$ 里即可。那么此时可以想到一个类似与 $dp$ 的思路来处理这个东西。$t1,t2,t3$分别表示在u的子树中的满足要求的 $1,2,3$ 元对的个数。遍历的 $u$ 的子节点 $v$ ，如果 $u$ 的辈分高于 $v$，那么显然可选的点数就是 $v$ 的子树大小，否则为 $n-u$ 的子树大小，设其为 $k$。$t3$显然是在 $t2$ 的基础上选一个，即$t2\times k$。$t2$ 是在 $t1$ 的基础上选一个，即$t1\times k$，$t1$ 就加上可选的 $k$ 个就行了，把统计完的 $t3$ 加起来就行了。

AtCoder Beginner Contest 313

A

模拟。

B

类似 $floyd$，若 $i>j$ 并且 $j>k$ 得出 $i>k$，最后对于 $i$ 判断即可。

C

求一下平均值，然后对于余数部分就把后面的减掉，最后加上绝对值之和/2就行。

D

没有看到不能重复。。。。询问 $[1,k+1]$ 去掉 $[1,k]$ 后的 $k$ 个数，得到k组关系，继续询问 $[1,k],[3,k+2],[4,k+3].....$得到 $n-k$ 组关系，通过这些关系就可以推值了，（这里的关系指值相不相等）

E

首先比较明显的是如果有两个非1数挨在一起就会-1。对于有解，因为i作用于i-1，所以考虑倒着统计。记当前的答案为ans，那么显然对于i(1<=i<n)，那么消掉他首先由s_i+1拆开（1次）然后是彻底消掉（ans * s_i+1次），加到ans里就行了，记得-1，因为最后一步长度为1的时候不需要操作。

KEYENCE Programming Contest 2023 Summer（AtCoder Beginner Contest 315）

A

对于每一个字符判断即可

B

首先找到他在哪个月，然后算天数就行

C

排个序最大的一定取，然后枚举另一个即可

D

有点没看懂题qwq，但感觉就是模拟，略了

E

感觉很显然的图论，对于一个书就指向所有他要看的，对于一条路径显然就是先看最下面的然后依次往上，所以从$1$ 开始往下 $dfs$ 就行了，但是要先 $dfs$ 子节点，因为要先处理要看的。

F

赛时正解想到了，但是细节没处理好挂了了。首先观察到性质：因为2^{c的增长非常快，可以估计大概当c>30的时候2}c已经太大了不可能跳c个成为最优解，所以只需要dp那些c<=30的情况即可。设dp(i, c)表示前i个，跳了c个的最短距离（不包含2^c，赛时这个一起算就挂了），那么我们考虑是从哪个点走过来的设他为k，此时他们之间的点显然都跳了但是我们知道这个数<=30，所以k的取值最多30，所以直接考虑转移柿子，显然就是dp_{k, c-(i-k-1)}+dis(k,i)，然后取个min就没了。最后答案就是min(dp_{n,c} + 2^c)

AtCoder Beginner Contest 319

A

存个表直接找就行。

B

枚举 $j$ 即可

C

$dfs$ 读法，答案是不失望的读法数 $/9!$

D

二分答案裸题，$check$ 就对于每个单词看看要不要换行并更新一下即可，最后判断行数 $<=m$ 即可

E

显然 $lcm(p_1,p_2,...p_{n-1})$ 是个循环，那么只需要处理 $0lcm(p_1,p_2,....,p_{n-1})-1$ 的答案即可，最后对于每个查询，整的部分直接算就行，零的前面已经预处理过了

ARC165

A

显然当 $n$ 有大于 $1$ 个质因子的时候 $Yes$，脑抽挂了 4 发，555

B

首先你排完序以后一定不变或更劣，既然字典序最大，那么就让第一个改变的数的位置尽量靠后。然后有初始最优区间 $[n-k+1,k]$，考虑看看能不能更优秀，设 $now$ 为当前的尝试的区间的开头，那么如果 $p_{now-1}<p_{now}$ 那么 $now$ 变成 $now-1$ 一定不劣，不停的移知道再移动会变劣为止，然后直接操作即可。

ABC320

A

暴力算一算即可。

B

直接找吧，取个max。

C

圆环，所以把每个都复制3遍，然后枚举最后数字相同且位置不同的那三个，设他们的下标为 $i,j,k$，则最后的时间为 $max(i,j,k)$，对这个东西取个 $min$。

D

明显的图论，$A_i=>B_i$，走过去就两个坐标分别加上边权的 $X_i,Y_i$ 即可，刷一遍 $dis$ 就行。

E

首先：在队里的人里面编号最小的显然一定排在最前面。然后开两个优先队列 $q1,q2$，$q1$ 存不在队里的人的回归时间和编号，$q2$ 存在队里的人的编号。每次显然就是 $q2.top()$ 来接，然后踢到 $q1$ 里存。这里 $q1$ 就按回来的时间从小到大排，这样具有单调性可以优化不少时间，注意在前面要把归队的全部从 $q1$ 挪到 $q2$ 里。

F

设 $f_{i,j,k}$ 表示到了 $X_i$，正的那趟到这里有 $j$ 的油， 反的那趟到这里至少有 $k$ 的油的最小花费，那么考虑转移，主导转移好些很多。设 $dis$ 为 从 $i$ 到 $i+1$ 的耗油数，那么对于 $X_{i+1}$ 可以：

1. 不加 $f_{i,j,k}=>f_{i+1,j-dis,k+dis}$
2. 正着到 $X_{i+1}$ 的时候加 $f_{i,j,k}=>f_{i+1,min(j-dis+F_{i+1}),k+dis}$
3. 反着到 $X_{i+1}$ 的时候加 $f_{i,j,k}=>f_{i+1,j-dis,k+dis-F_{i+1}}$

最后一段路单独领出来用 $dp$ 处理一下就好了捏：

对于 $d{p}_{n-1,j,k}$ ，现在要从 $n-1$ 走到 $n$，那么就是看看能不能 $n-1=>n=>n$ 以后油还不小于 $k$，设 $dis$ 为$n$ 和 $n-1$ 的距离，然后这个就判一下 $k\le j-2\ast dis$，如果满足就可以，取个 $min$。

ABC321

A

直接模拟判即可。

B

就从0~100分别 $check$ 一下就好了。

C

直接暴力 $dfs$ 出来所有满足要求的数，然后打表输出即可。

D

二分板子。把 $b$ 排个序，对于每一个$i$ 来算他和所有 $b_j$ 的答案，设最后一个满足 $a_i+b_j\le p$ 的 $j$ 为 $l$，那么显然 $a_i$ 就和 $[1,l]$ 的和都是不被 $P$ 影响的，后面的都是 $P$，前面的用前缀和算一下，后面直接算就行。

E

分为在 $x$ 子树内的答案和在子树外的答案。设 $f(n,x,k)$ 表示 $n$ 个点 $x$ 到其子树内距离为 $k$ 的点有多少个。子树内的就是 $f(n,x,k)$，然后枚举一下 $x->u->y$ 这个 $u$，显然最多 $log$， $x->u$ 是固定的，$u->y$ 的 $y$ 的个数就是 $f(n,u,k-dis(u,x))$.

F

回退背包板子，没啥好讲的。就 + 的时候把所有的方案数加上 $f_{j-x}$，- 的时候就做逆操作就行了捏。