羊村懒王

这个屌丝很懒，什么也没留下！

热门标签

Java力扣热门题目简单部分合集（共23道）_java笔试测评力扣

作者：羊村懒王 | 2024-02-15 21:50:43

踩

java笔试测评力扣

文章目录

前言
1、两数之和(哈希表，双指针，数组)
2、有效的括号（栈，哈希表）
3、合并两个有序链表（递归，迭代）
4、最大子数组和（动态规划，分治，贪心）
5、爬楼梯（迭代，递归，动态规划，数学）
6、买卖股票的最佳时间（贪心，双指针，动态规划）
7、二叉树的中序遍历（Morris中序遍历，递归，迭代）
8、对称二叉树（递归，迭代）
9、二叉树的最大深度（BFS，DFS）
10、只出现一次的数字（哈希表，异或）
11、移动零（双指针）
12、多数元素（哈希表，排序，随机化，分治）
13、最小栈（栈）
14、比特位计数（Brian Kernighan算法，动态规划）
15、汉明距离（Brian Kernighan 算法，异或）
16、找到所有数组中消失的数（哈希表，Set集合）
17、环形链表（快慢指针，哈希表）
18、相交链表（哈希表，双指针）
19、反转链表（栈，递归，迭代，双指针，头插法）
20、回文链表（双指针）
21、翻转二叉树（BFS，DFS，递归）
22、二叉树的直径（BFS）
23、合并二叉树（BFS，DFS）
总结

前言

涵盖热门100题中的所有简单部分的题目，把第一遍做的笔记重新整理了一下放到一起了，修改了一些错误的部分，把没能实现的都实现了一下，去掉了重复的代码，只留下了最精炼的各种方法的代码

我也是一个力扣新手，很多算法并不是特别掌握，也是摸着石头过河，但我的经验和总结是很不错的学习内容，大家可以好好看看我的分析，思考，错误过程，如何解决，总结

好的题目是值得反复回看的，大家也是为了找工作或者提升自己，这些经典题目涵盖了很多的思路和方法，我后面做中等题或者是困难题的时候，很多简单题的思路都启发了我，大家不要着急，想一口吃成个胖子，把我的总结好好的跟自己的思路对比看看，重点掌握每个题目的一两个最重要的思路，然后再学习其他的扩展思路，吃透，会对后面的刷题有很大的帮助，如果是着急，囫囵吞枣，大致看完就过去，效果不会太好

我总结的时候，吸取了很多网友的评论和解答，结合自己的理解形成了这些题目的笔记，我又整理了一遍，确保没有不是重要的东西存在，每个题都总结了多种方法和思路，希望可以给大家帮助

希望大家关注，点赞，收藏，支持一下我，后面还会为大家其他重点的简单题，以及更新力扣热门的中等和困难的题目，有需要我的这个文档的，可以关注私信我，可以把我的这个吸收作为你自己的笔记，也可以节省一些时间。

1、两数之和(哈希表，双指针，数组)

1、问题描述

给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出和为目标值 target 的那两个整数，并返回它们的数组下标。

你可以假设每种输入只会对应一个答案。但是，数组中同一个元素在答案里不能重复出现。

你可以按任意顺序返回答案。

2、示例

示例 1：

输入：nums = [2,7,11,15], target = 9
输出：[0,1]
解释：因为 nums[0] + nums[1] == 9 ，返回 [0, 1] 。
1
2
3

示例 2：

输入：nums = [3,2,4], target = 6
输出：[1,2]
1
2

示例 3：

输入：nums = [3,3], target = 6
输出：[0,1]
1
2

3、提示

2 <= nums.length <= 10^4
-10^9 <= nums[i] <= 10^9
-10^9 <= target <= 10^9
只会存在一个有效答案

4、进阶

你可以想出一个时间复杂度小于 O(n2) 的算法吗？

5、具体解法（暴力遍历，哈希表，二分法）

//2022年3月21日10:58:28

//解法一，用暴力枚举的方式,注意边界
/*
public class Solution {
    
    //public static void main(String[] args) {
    //为什么不用写这个，直接就是执行这个类,写了这个也不行，因为会提示非法的开始，没有调用程序的部分，不过我应该会写了

        //首先方法是数组类型的，因为要返回的是数组类型。两个参数也是对应的写好，符合写程序的思路
        public int[] twoSum (int[] nums, int target){
            int n = nums.length;
            //i是外层循环，而且只需要判断到倒数第二个数即可，因为最后一个数由内层循环提供
            for (int i = 0; i < nums.length - 1; i++) {
                //j是内层循环，从i+1开始，且需要判断到最后一个数
                for (int j = i + 1; j < nums.length; j++) {
                    if (nums[i] + nums[j] == target) {
                        //当符合条件的时候就输出一个数组，里面的内容是此时的i和j，也就是下标
                        return new int[]{i, j};//这个数组连名字都没有也可以？                       
                    }
                }
            }
            return new int[0];//当for循环都跳出了，还是没有，就返回一个空数组，这个写法就是标准的返回空数组的写法
        }
     }
*/


//解法二：用HashMap的方式，哈希表
//并不是先将所有数据都放进HashMap，而是从数组第一个数先开始判断target-x在哈希表中是不是存在
//然后再将这个数放进Map中，可以避免自己跟自己匹配
//注意：为什么是containsKey而不是value，因为存的时候是数组值在key里，下标再value里
/*
public class Solution {
        public int[] twoSum(int[] nums, int target) {
            //创建一个HashMap集合，Map是键值对的形式，而HashMap是键唯一
            Map<Integer, Integer> hashtable = new HashMap<Integer, Integer>();
            for (int i = 0; i < nums.length; ++i) {
                //判断每一个值x对应的target-x是不是存在
                if (hashtable.containsKey(target - nums[i])) {//因为这个map的键值对种是下标是值，键反而是数组中是数值
                    //存在就返回两个下标，其中的target-x下标可以用HashMap的get方法获得
                    return new int[]{hashtable.get(target - nums[i]), i};
                }
                hashtable.put(nums[i], i);//而且要注意键值对，谁是键，谁是值
            }
            return new int[0];
        }
     }
*/


//解法三、双指针，二分大法
//这其实是一道搜索题，固定一个数后，就是如何找到另外一个数（target - [i]）。
//因为是数组，要利用随机访问的能力，因此内部loop可以用双指针从两头往中间找，这样可以节省一半的时间，整体时间复杂度会到O(nlogn)，仍要注意边界。
   
/*
public class Solution {
    public int[] twoSum(int[] nums, int target) {
        int[] result = {0, 1};
        if (nums.length <= 2) {
            //回顾来看，因为题目强调了数组至少会有两个数，所以才是这么写的，写成==2也可以
            return result;
        }

        for (int i = 0; i < nums.length - 1; i++) {
            result[0] = i;//这个reault[0]和reault[1]的写法也值得去学习一下
            int x = target - nums[i];
            //对内部循环做双指针寻找，但我感觉本质还是遍历呢，但执行时间减了很多
            //对自己最初疑问的解答：因为他是从两端同时开始的，相当于每次只遍历n/2次，所以这一层的复杂度会降到O(logn)
            for (int j = i + 1, k = nums.length - 1; j <= k; j++, k--) {
                if (nums[j] == x) {
                    result[1] = j;
                    return result;
                }
                if (nums[k] == x) {
                    result[1] = k;
                    return result;
                }
            }
            //你看其本质就是循环的时候不是一个个去看，而是两个两个去看，但还是全看了
            //所以说循环是for遍历的内容，而for里面要操作的多少并不是算进循环的，虽然所有数都判断，但是循环只跑了n/2次
        }
        return result;
    }
}
*/


//解法四：内外都用双指针，四分大法
//其实主loop也可以采用二分法，用双指针从两头往中间遍历，这样又可以节省一半的时间。
//还可以做剪支，如果主loop的双指针之和恰好是target，那就直接返回，剪支在分析效率的时候可能帮助不大，但在真实的运行时，能大大提高效率。
//在不借助额外的数据结构的前提下，这是最优解，从运行结果来看，时间是0，严格来说是O(n/2*logn)。
/*
public class Solution {    
    public int[] twoSum(int[] nums, int target) {
        int[] result = {0, 1};
        if (nums.length <= 2) {
            return result;
        }

        for (int i = 0, j = nums.length - 1; i < j; i++, j--) {
            if (nums[i] + nums[j] == target) {
                //主loop的双指针之和恰好是target
                result[0] = i;
                result[1] = j;
                return result;
            }

        //这次是一次进来两个数做比较，i和j，然后内层会从i+1到j-1之间去找遍历找数，也是通过二分法找两个数分别和i，j去比较
            int x = target - nums[i];
            int y = target - nums[j];//这两个的作用就是后面写起来可以清晰一点，把一个长的用一个符号来代替
            for (int k = i + 1, m = j - 1; k <= m; k++, m--) {
                result[0] = i;
                if (nums[k] == x) {
                    result[1] = k;
                    return result;
                } else if (nums[m] == x) {
                    result[1] = m;
                    return result;
                }

                result[1] = j;
                if (nums[k] == y) {
                    result[0] = k;
                    return result;
                } else if (nums[m] == y) {
                    result[0] = m;
                    return result;
                }
            }
        }
        return result;
    }
}
*/

    
//解法五：二分加Map
//其实一开始没想到用Map，因为以往做ACM的时候，一般来说不让直接使用标准库里的东西，这本是一个搜索，前面的四分法能满足要求，额外再实现一个Map，不太划算。
//注意，题目中说返回结果不要求有一定的顺序，这就暗示了，可以使用Map来做内层的搜索，外层仍要遍历，内层用Map来搜索，整体效率会达到O(n)。
//同时，受四分大法启发，外层主loop，其实仍可以用二分大法，这样时间复杂度又提高到O(n/2)。
/*    
public class Solution {
    public int[] twoSum(int[] nums, int target) {
        int[] result = {0, 1};
        if (nums.length <= 2) {
            return result;
        }

        Map<Integer, Integer> valueToIndex = new HashMap<>();
        for (int i = 0, j = nums.length - 1; i <= j; i++, j--) {
            if (nums[i] + nums[j] == target) {
                //这种情况是第一个和最后一个恰好就是要的两个数
                result[0] = i;
                result[1] = j;
                break;
            }
            int x = target - nums[i];
            if (valueToIndex.containsKey(x)) {
                result[0] = i;
                result[1] = valueToIndex.get(x);
                break;
            }
            x = target - nums[j];//这个比解法四还要省了一个变量的空间
            if (valueToIndex.containsKey(x)) {
                result[0] = j;
                result[1] = valueToIndex.get(x);
                break;
            }
            //如果没找到，就把这个数存进哈希表，避免重复的数字使用
            valueToIndex.put(nums[i], i);
            valueToIndex.put(nums[j], j);
        }

        return result;
    }
  }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178

6、收获

这种求和的题目，有数组的，可以想到暴力解决，用循环进行遍历
这种题目的目的，其实是找一个x并判断对应的target-x是否存在，这种理解题目的思路是我从没有过的，要学习
正是通过上面的那种理解，可以发现暴力法的问题在于寻找的过程是遍历全部，时间复杂度高，所以采用创建哈希表的方式，这种方式可以将两层for循环的O(n^2)降低到O(n)。原理是将所有数组元素先放进哈希表，这样是n个数据，遍历放进去是O(n)，而查的过程，不用遍历去找，哈希表是可以直接根据键值对进行定位的，所以整体的查找过程是O(n)的时间复杂度，但是多以哈希表的存储空间，所以是用空间换时间，空间复杂度由O(1)变为了O(n)。这种用空间换时间的思路要学会。
对于HashMap和containsKey()和get()有了更深入的理解，注意谁是键谁是值，这个是在存储的时候确定了的
对于return也有了新认识，需要返回多个数值的时候，可以使用数组来进行，而且return new int[]{里面是数组的内容}，直接就可以返回{内容}，不需要给数组起一个名字的。如本题就是 return new int[]{i, j};
写程序的思路：输入输出类型，循环边界，特殊的情况，然后才是具体的方法使用
有序：对撞指针或者二分法，无序：哈希表
发现一道题的解法太多了，还有没收录进来的 排序加数据封装加折半查找 这样的方法，可以以后再看
return new int[0]; 标准的返回空数组的写法
return new int[]{i, j}; 直接返回一个数组以及相应内容的写法
Map<Integer, Integer> valueToIndex = new HashMap<>(); 标准的哈希表创建代码

2、有效的括号（栈，哈希表）

1.问题描述

给定一个只包括 ‘(’，‘)’，‘{’，‘}’，‘[’，‘]’ 的字符串 s ，判断字符串是否有效。

有效字符串需满足：

左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。

2.示例

示例 1：

输入：s = "()"
输出：true
1
2

示例 2：

输入：s = "()[]{}"
输出：true
1
2

示例 3：

输入：s = "(]"
输出：false
1
2

示例 4：

输入：s = "([)]"
输出：false
1
2

示例 5：

输入：s = "{[]}"
输出：true
1
2

3.提示

1 <= s.length <= 10^4
s 仅由括号 ‘()[]{}’ 组成

4.具体解法（栈加哈希表判断，栈加直接判断，栈加ASCII值判断，repalce方法解决）


//方法一：使用栈加哈希表的思路
/*
public class Solution {
    public boolean isValid(String s){
        int n=s.length();
        if(n%2==1){//如果字符串长度是奇数，那肯定是不能匹配的
            return false;
        }
        Map<Character,Character> pairs=new HashMap<>();//创建一个HashMap来存储每一种括号，键是右括号。值是左括号
        pairs.put(')','(');
        pairs.put(']','[');
        pairs.put('}','{');//为什么键是右括号呢，后面分析
        //将括号存储好后，就可以将字符串进栈进行判断了
        //字符串每个字符依次进栈，只要遇到左括号就入栈
        //遇到右括号就从栈中取出一个进行匹配（用哈希表），依次类推，直到字符串遍历完毕，栈中无括号，则是有效的

        Deque<Character> stack=new LinkedList<>();
        for (int i=0;i<n;i++){
            //charAt(i),返回字符串指定索引处的char值，序列的第一个char值是索引0 ，下一个索引为1 ，一次类推，像数组索引一样
            char ch=s.charAt(i);
            //containsKey的作用是判断哈希表中是不是有这个键（也就是右括号），如果有，说明此时判断的字符是右括号
            if(pairs.containsKey(ch)){
                //peek()方法是只查看，不从栈中取出
                //pop()是查看并从栈中取出
                if(stack.isEmpty()||stack.peek()!=pairs.get(ch)){
                    return false;//已知是右括号了（因为有这个键），如果此时栈是空的，或者对应的左括号不匹配就说明不匹配
                }
                else{
                    stack.pop();//如果不属于前面的情况，那说明右括号和左括号匹配上了，那么将栈中的左括号拿出来即可
                }

            }
            else{
                stack.push(ch);//如果通过containsKey发现不存在这个键，那么说明是左括号，那么就应该入栈
            }
        }
        return stack.isEmpty();//字符串全遍历完毕了，如果栈是空的那么就是匹配好了，如非空，就没匹配好。所以用isEmpty就正好对应了这个返回值的需求
    }
}
 */


//方法二：是使用了栈而没用哈希表的一种方法，效率优于使用哈希表
//直接就是用获得的字符进行判断，省空间，时间复杂度是一样的
/*
class Solution {
    public boolean isValid(String s) {
        Stack<Character> stack=new Stack<>();//这个就是用Stack类创建的栈，而不是用Deque
        for(int i=0;i<s.length();i++){
            char c=s.charAt(i);
            if(c=='('||c=='['||c=='{'){
                stack.push(c);
            }//如果是左括号，那么push进栈
            else
         if(stack.isEmpty()||c==')'&&stack.pop()!='('||c==']'&&stack.pop()!='['||c=='}'&&stack.pop()!='{'){
                    //如果不是左括号，那么说明是右括号
                    //此时如果栈是空的，或者此时判断的右括号是），而栈顶的元素不是（，或者}{][不能匹配到，那么就输出false
                    return false;
                }
        }
        return stack.isEmpty();
    }
}
 */
 
 

//方法三：使用replace方法的巧妙思路，效率低，但是代码很短小精悍
//replace(s1,s2),用s2串去替换所有的s1串
/*
class Solution {
    public boolean isValid(String s) {
        while(true){
            int len=s.length();
            s=s.replace("()","");//用空字符替换匹配的括号
            s=s.replace("{}","");
            s=s.replace("[]","");
            //执行完一轮之后，如果长度变了，说明有匹配的，所以返回去再做赋值和匹配。
            //如果没变，那说明没有一组可以匹配的了，此时判断字符串的长度是不是0，如果是0，那么会返回true
            if(s.length()==len){
                return len==0;
            }
        }
    }
}
 */



//方法四：使用ASCII加字节数组进行判断
//其实就是将字符类型通过数字来进行判断了，而转换的途径就是ASCII
//而且，匹配的括号应该相差的ASCII值是1或者2，由此可以进行括号是否匹配的判断
/*
class Solution {
    public boolean isValid(String s) {
        byte[] s_byte = s.getBytes();//字符串转化为byte数组，即对应字符的ASCII码表。
        Stack<Byte> stack = new Stack<>();//创建栈。
        byte symbol = 0;//这个目标一直是栈顶的那个元素，等待被消除
        if(s.length() % 2 != 0){
            return false;  //奇数个字符直接返回false。
        }
        for(int i = 0; i < s.length(); i++){
            if(s_byte[i] == 40 || s_byte[i] == 91 || s_byte[i] == 123){
                //下一个字符为(、{、[之一时，压栈。
                stack.push(s_byte[i]);//被消除者为(、{、[ ，将这些字符压入栈中。
                symbol = s_byte[i];  //修改消除目标为当前最新压入的被消除者。
            }
            else if(s_byte[i] == (symbol + 1) || s_byte[i] == (symbol + 2)){
                //下一个字符为 )、}、]之一时，弹栈。
                stack.pop();
                symbol = stack.empty() ? 0 : stack.peek(); //消除成功，更换新的消除目标。
            }
            else{
                return false;
            }
        }
        while(stack.empty()){  //结束且栈中无剩余。
            return true;
        }
        return false;   //栈中有剩余。
    }
}

 */


//解法五：ASCII值加字符数组
//类似于方法四，只不过更简洁一点，采用的s.toCharArray()将s变成字符数组进行判断，而方法四是变成字节数组
class Solution {
    public boolean isValid(String s) {
        
        if (s.isEmpty()) return true;//if的代码块只有一句，可以不加大括号
        
        //一种全新的判断是不是偶数的方式，跟1按位与，结果是1则为奇数，底层逻辑应该是二进制
        if ((s.length() & 1) == 1) return false;
        
        //发现这几种方法中，创建栈的方式各种各样，都可以，新手不要拘束，各自优点可以以后慢慢了解
        Deque<Character> stack = new ArrayDeque<>();
        
        //s.toCharArray()是将串s变成字符数组
        for (char ch : s.toCharArray()) {
            // '('，')'，'{'，'}'，'['，']' 的 ASCII 码分别是 40、41、91、93、123、125
            if (ch == '(' || ch == '[' || ch == '{') {
                stack.push(ch);
            } else if (stack.isEmpty() || Math.abs(ch - stack.pop()) > 2) {
                return false;
            }
        }
        return stack.isEmpty();
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152

5.收获

对于每一道题都应该想到他的特殊情况，比如这道题，奇数不可能匹配，那就为我们的遍历省下了一半的工作
学会了栈的定义方式以及pop，push，peek方法的使用，pop是出栈，peek是查看，push是入栈
了解了关于Deque接口取代Stack做栈的创建的思想，可以见零散知识点，具体可以见另一篇文章https://blog.csdn.net/humor2020/article/details/123654251
匹配的括号应该相差的ASCII值是1或者2，这个结论要了解。
一种全新的判断是不是偶数的方式，跟1按位与，结果是1则为奇数，底层逻辑应该是二进制（位与：全1为1）
对于containsKey和containsValue方法的理解，是用来判断表中是不是有这个键或者值，而不是判断键或值对应的值或键是否匹配
复习了字符串的charAt方法。charAt(i),返回字符串指定索引处的char值，序列的第一个char值是索引0 ，下一个索引为1 ，一次类推，就像数组索引一样
复习了字符串的replace方法。s=s.replace(s1,s2)，得用一个字符串对象去调用，用s2串去替换s中的所有的s1子串
学到的解题思路有：哈希表去存储键值对做匹配，栈的先进后出思路使用，ACSII差值进行判断匹配
return stack.isEmpty();或者是return len==0;这样的写法是比较巧妙的，应该学会，用逻辑表达式的值来返回ture或者false，就不用我自己多写一步赋值了，直接返回。
Deque stack=new LinkedList<>();

Deque stack = new ArrayDeque<>();

Stack stack=new Stack<>();

以上三种都是创建栈的写法，建议使用第一个，另外两个也不是不可以

3、合并两个有序链表（递归，迭代）

1.问题描述

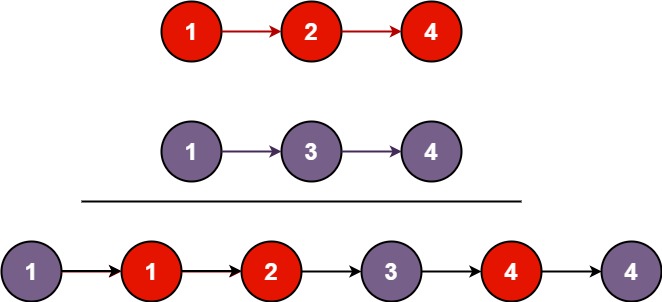
将两个升序链表合并为一个新的升序链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。

2.示例

示例 1：

输入：l1 = [1,2,4], l2 = [1,3,4]
输出：[1,1,2,3,4,4]
1
2

示例 2：

输入：l1 = [], l2 = []
输出：[]
1
2

示例 3：

输入：l1 = [], l2 = [0]
输出：[0]
1
2

3.提示

两个链表的节点数目范围是 [0, 50]
-100 <= Node.val <= 100
l1 和 l2 均按非递减顺序排列

4.具体解法（递归，迭代）

解法一的辅助理解图：

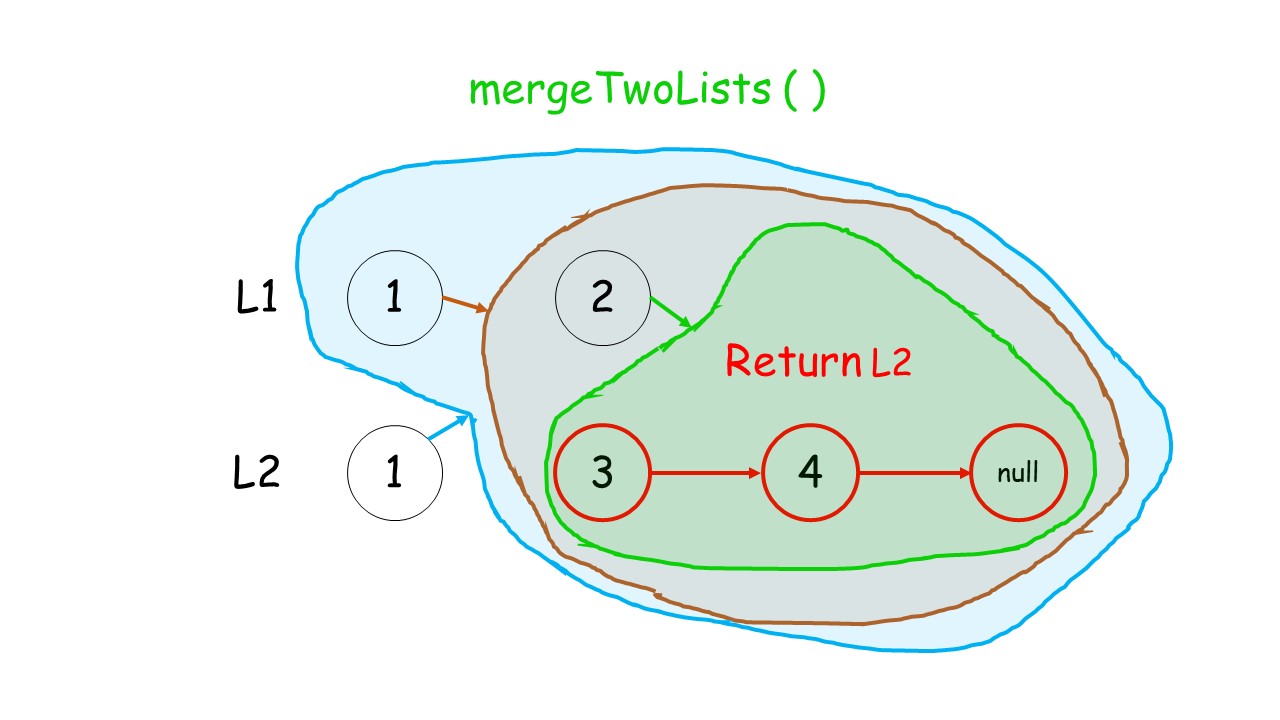
//解法一：使用递归的方式，下面的图非常清晰的展示了关系。

//两个链表头部值较小的一个节点与剩下元素的 merge 操作结果合并。

//如果 l1 或者 l2 一开始就是空链表 ，那么没有任何操作需要合并，所以我们只需要返回非空链表。否则，我们要判断 l1 和 l2 哪一个链表的头节点的值更小，然后递归地决定下一个添加到结果里的节点。如果两个链表有一个为空，递归结束。


/**
 * 这是链表的内容，展示在这里可以方便去调用
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode mergeTwoLists(ListNode l1, ListNode l2){
//我好像明白了为什么必须方法名叫mergeTwoLists，因为我们写的类是解决问题的类，而调用的测试类应该在网页的后台，是写好的，如果不按着人家给的规定好的来写，那么肯定会报错。
        if (l1 == null){
            return l2;
        }
        else if(l2 == null){
            return l1;//如果s1或者s2是空的，那么就返回非空的那个就ok了
        }
        else if (l1.val<l2.val){
            l1.next=mergeTwoLists(l1.next,l2);
         //一开始都是在头结点的位置上，如果l1的头结点小于l2的头结点，那么就让小的那个结点指向剩余部分（继续调用递归）
         //然后就是l1的下一个结点跟l2的头结点开始比较了，以此类推的去调用，直到有一个串移动到空的位置了
         //这个时候递归调用就会进入到上面那两个if的情况之一，然后就有了返回值，这个返回值再给调用者，就会将所有结点开始连起来了
            return l1;//链接完毕后，因为最小的节点是l1的头结点，所以返回l1就是整个连接好的新链
        }
        else{
            l2.next=mergeTwoLists(l1,l2.next);
            return l2;//这个就是最小的结点是l2的头结点，所以返回的是这个结点
        }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

//解法二：使用迭代的方式

//我们可以用迭代的方法来实现上述算法。当 l1 和 l2 都不是空链表时，判断 l1 和 l2 哪一个链表的头节点的值更小，将较小值的节点添加到结果里，当一个节点被添加到结果里之后，将对应链表中的节点向后移一位。
class Solution {
    public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
        //创建一个链表对象，传递的参数是结点的val，next:默认为null，这是一个参数的构造方法
        ListNode prehead = new ListNode(-1);
        
        //设定一个哨兵节点 prehead ，这可以在最后让我们比较容易地返回合并后的链表
        //最后的返回值是 preHead.next，也就是说这个哑节点的初始值大小并不重要，
        //因为在最后并不会返回它，返回的是它后面链表的头节点preHea.next
        //这里可以是-1 也可以是任何值，不影响返回结果。

        ListNode prev = prehead;
        //这句话的意思是prev和prehead都指向同一个结点，后面prev会不停的移动（游标），那么最一开始的头结点就找不到了，
        //所以用prehead定位所以叫哨兵，
        //而且是只跟prev的第一个结点指向同一个，后面prev.next再去指向新的，就不会影响prehead了
        // prehead头结点是为了记录链表起始位置，prev是要往下next遍历的，一个是游标一个是哨兵。
        
        //只要两个链表有一个为空就跳出循环
        while (l1 != null && l2 != null) {
            if (l1.val <= l2.val) {//开始比较两个链表的头结点
                prev.next = l1; // prev.next代表链表的下一个结点是l1的当前结点
                l1 = l1.next;//被操作的链表就指向下一个结点继续重复操作
            } 
            else {
                prev.next = l2;//与上面的同理
                l2 = l2.next;
            }
            prev = prev.next;
            //因为前面有prev.next=l1这样的操作，所以我们再把这个操作的节点往后移动一位，再继续去指新的
            //我指向了你，接下来该由你去指向别的结点了。
        }

        // 合并后 l1 和 l2 最多只有一个还未被合并完，我们直接将链表末尾指向未合并完的链表即可
        prev.next = l1 == null ? l2 : l1;

        return prehead.next;//返回的是链表所指的下一个结点，恰恰就是第一次比较时两个链表的头结点中小的那个，也是整个新链表中的头结点
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

5.收获

在链表的题目中，这些l1，l2之类的都是链表的结点，类型是ListNode，不要简单的当成一个变量
我理解的递归，首先是递归调用同一个函数，我最外层的函数输出需要用到再调用这个函数去计算的结果，直到某个特殊值，会直接返回一个结果，然后层层返回，最后得到最外层的输出结果
第一层龟的输入，是第二层龟的输出，如此类推。
对于链表的定义有了新的认识，需要去自定义一个ListNode类，但好像IDEA里自动就有，在力扣里也不需要去定义，更多关于链表的了解可以看另一篇文章https://blog.csdn.net/humor2020/article/details/123683086
对于哨兵结点的使用有了新认识，链表题目时经常用到的写法，由于在对链表进行重新排列、打断、合并等等操作时，链表的头节点往往会发生移动变得“破朔迷离”，故在一开始我们设定一个哨兵节点，这可以在最后让我们比较容易地返回合并后的链表。具体使用可以看另一篇文章https://blog.csdn.net/humor2020/article/details/123683097
对于迭代的操作也有了新的理解：是一种重复反馈的过程，是一种不断用变量的旧值递推新值的过程，以这道题为例子，就是我指向你了，然后你接替我的身份，你再继续去指，直到满足某种条件停止，最后我们就形成了一个长长的链。
见识到了新名词“哑结点”，“游标结点”，“哨兵结点”。
ListNode prehead = new ListNode(-1); 创建哑结点的标准代码，执行new ListNode(-1)，就是创建一个对象{val: -1, next: null}
ListNode prev = prehead; 一定要掌握这个，这个是使pre 和prehead指向同一个结点。常用于一个作为游标，一个作为哨兵。

4、最大子数组和（动态规划，分治，贪心）

1.问题描述

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

子数组是数组中的一个连续部分。

2.示例

示例 1：

输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。
1
2
3

示例 2：

输入：nums = [1]
输出：1
1
2

示例 3：

输入：nums = [5,4,-1,7,8]
输出：23
1
2

3.提示：

1 <= nums.length <= 10^5
-10^4 <= nums[i] <= 10^4

4.进阶：

如果你已经实现复杂度为 O(n) 的解法，尝试使用更为精妙的分治法求解。

5.具体解法（暴力循环，贪心算法，动态规划，分治法）

方法一：暴力循环（不能AC，因为最后一个数组特大，运行时间超出要求）
//自己独立完成的代码，使用了暴力循环的方式，调试了三次终于从只能通过1/3用例到2/3到几乎全完成，到最后一次是超长数组通过不了（超出时间限制）
//对于调试代码有了新的理解和经验，一种是自身逻辑入手，一种是跟随失败案例循环一遍自己的代码看哪里哪一步出现了问题
//对于最后的超出时间，已经是超出我的目前水平了，那个数组得有好几千上万个数据，我这种暴力循环的思路，应该是不能解决这种问题的，而且自己写的是暴力循环中的比较笨的
//逻辑不够清晰，只能缝缝补补似的完成需求，不过这是个好的开始

//自己想出来的最简单的暴力遍历，我们以四个数字为例，所有的连续子数组情况无非是（1,12,123,1234,2,23,234,3,34,4），
所以我们去按照这种思路遍历数组即可，定义一个max存储当前的最大值，
用s去存储每一次计算的新的和，跟max比较，s>max就把s赋值给max，直到遍历结束，返回max

/*
class Solution {
    public int maxSubArray(int[] nums) {
        //因为我后面是比较每个值跟他的大小，他来存储最大值，有一种数组里面全是负数，那么这个max的初始值就不适合设为0
        //后面也学到了，这里可以使用Integer的成员变量：MIN_VALUE，是-(2的31次方),没有比他更小的了。避免像-1000这种又不行。
        int max=-999;//最后要返回的最终的最大值

        int s=0;//这个s是临时的最大值
        for(int i=0;i<nums.length;i++){
            if(i==nums.length-1){//如果是最后一个数，因为我会计算它加他后面的数，如果是最后一个数，那就没有它后面的数了，做加法也是不合理的，会报错数组越界，所以我单独把这个拿出来进行判断了
                s=nums[nums.length-1];
                if(s>max){
                    max=s;
                }
            }
            else{
                int k=nums[i];//这个k的作用是存储刚刚加过的数的和，防止出现每次都是挨着的两个数相加，而不是全部数相加的情况
                for(int j=i;j<nums.length-1;j++){
                    if(nums[j]>max){
                        max=nums[j];//这里需要单独判断一下是不是第一个数就大于max，要不然如果是[2，-1]的这种情况，那么就会忽略掉max=2
                    }
                    s=k+nums[j+1];//因为j=i，而且i判断过了不是数组最后一个数，所以是可以确定必然有nums[j+1]的
                    k=s;
                    if(s>max){
                        max=s;
                    }
                }
            }
        }
        return max;//当所有的都遍历完成，那么就返回此时的最大值max
    }
}
 */


//补上一个可以成功提交的暴力解法
//可以对比一下，自己写的有多差
//通过这个可以发现，如果我把我的那个int s=0;写在第一层循环内，第二层循环外，而不是写在第一层循环外的话，就不用去再创建一个k了
//而且人家是加nums[j],所以也不用特别去判断一下最后一个数的情况
/*
class Solution {
    public int maxSubArray(int[] nums) {
        int max = nums[0];
        int n = nums.length;
        for (int i = 0; i < n; i++) {
            int sum = 0;
            for (int j = i; j < n; j++) {
                sum += nums[j];
                if (sum > max){
                    max = sum;
                }
            }
        }
        return max;
    }
}
*/



//方法二：动态规划
//首先得去理解这种思路：找每个数作为结尾的数字的情况下的最大值即可
//用f(i)来表示以i为结尾的最大值
//为什么呢，以[1,2,3,4]为例，以1为结尾的就是[1]，以2为结尾的可以是[1,2]或者[2]，而[1,2]可以看做是问题1加上数字2
//再来一个例子，就更清晰了，以3为结尾的是[1,2,3]或[2,3]或[3]，可以看做是问题2的两种情况加上数字3
//我们用一个变量pre来维持f(i) 动态规划状态转移式: f(i) = max{f(i-1) + num,num},我们还需要一个变量来存储接结果返回值

/*
class Solution {
    public int maxSubArray(int[] nums) {
        int pre = 0, maxAns = nums[0];
        for (int x : nums) {
            pre = Math.max(pre + x, x);//这个是用来算每一个数做结尾的时候的最大值
            maxAns = Math.max(maxAns, pre);//这个是比较i做结尾的最大值和当前的最大值，取大的作为新的最大值
        }
        return maxAns;
    }
}
*/


//方法三：贪心算法
//动态规划的是首先对数组进行遍历，当前最大连续子序列和为 sum，结果为 ans
//如果 sum > 0，则说明 sum 对结果有增益效果，则 sum 保留并加上当前遍历数字
//如果 sum <= 0，则说明 sum 对结果无增益效果，需要舍弃，则 sum 直接更新为当前遍历数字
//每次比较 sum 和 ans的大小，将最大值置为ans，遍历结束返回结果

//其实这道题可以这么想： 
//1.假如全是负数，那就是找最大值即可，因为负数肯定越加越大。
//2.如果有正数，则肯定从正数开始计算和，不然前面有负值，和肯定变小了，所以从正数开始。
//3.当和小于零时，这个区间就告一段落了，然后从下一个正数重新开始计算(也就是又回到 2 了)。而 dp 也就体现在这个地方。

//这个理解也很好，就是我前面的sum如果小于零，那再去加新的数字肯定是不好的，所以直接把它舍掉，从最新的数字这里是最大值继续
//也有人说这种叫贪心，方法二才算dp（动态规划）

//贪心或者说也是一种动态规划的一个代码
/*
class Solution {
    public int maxSubArray(int[] nums) {
        int ans = nums[0];
        int sum = 0;
        for(int num: nums) {
            if(sum > 0) {
                sum += num;
            } 
            else {
                sum = num;
            }
            ans = Math.max(ans, sum);
        }
        return ans;
    }
}
*/


//方法四：分治方法
//将原数组划分为左右两个数组后，原数组中拥有最大和的连续子数组的位置有三种情况。
//情况1. 原数组中拥有最大和的连续子数组的元素都在左边的子数组中。
//情况2. 原数组中拥有最大和的连续子数组的元素都在右边的子数组中。
//情况3. 原数组中拥有最大和的连续子数组的元素跨越了左右数组。
//分别求出，3中情况的最大和，取最大，就是原数组的连续子数组的最大和。

//而在求左或右子数组的时候，还要继续将他们俩再分成三种情况去求，直到子数组只剩一个元素的时候，开始一层层返回

/*
class Solution {
    public int getMax(int[] nums, int low, int high) {
        // 如果子数组只有一个元素，这个元素就是子树组的最大和。
        if (low == high) {
            return nums[low];
        }
        int mid = low + (high - low) / 2;
        // 求左数组的最大和
        int leftMax = getMax(nums, low, mid);
        // 求右数组的最大和
        int rightMax = getMax(nums, mid + 1, high);
        // 求跨越情况的最大和
        int crossMax = getCrossMax(nums, low, mid, high);
        // 返回最大
        return Math.max(Math.max(leftMax, rightMax), crossMax);
    }
    
    // 求跨越情况的最大和
    public int getCrossMax(int[] nums, int low, int mid, int high) {
        // 从中间向左走，一直累加，每次累计后都取最大值，最后得到的就是从中间向左累加可得到最大和
        int leftSum = nums[mid];
        int leftMax = nums[mid];
        for (int i = mid - 1; i >= low; i--) {
            leftSum += nums[i];
            leftMax = Math.max(leftMax, leftSum);
        }
        // 从中间向右走，一直累加，每次累计后都取最大值，最后得到的就是从中间向右累加可得到最大和
        int rightSum = nums[mid+1];
        int rightMax = nums[mid+1];
        for (int i = mid + 2; i <= high; i++) {
            rightSum += nums[i];
            rightMax = Math.max(rightMax, rightSum);
        }
        // 向左累加的最大和加上向右累加的最大和，就是跨越情况下的最大和
        return leftMax + rightMax;
    }

    public int maxSubArray(int[] nums) {
        return getMax(nums, 0 , nums.length - 1);
    }
}
 */
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178

6.收获

学习到了动态规划的概念，首先要有这个思路，然后找到f（i），以及相应的状态转移方程。

题目只要求返回结果，不要求得到最大的连续子数组是哪一个。这样的问题通常可以使用「动态规划」解决。

动态规划的思路就是自底向上，从如果只有一个元素的最优解到有n个元素的最优解。
对于动态规划和贪心的区别也有所了解：

贪心是每一步的最优解都是由上一步的最优解推出来的，而上一步的最优解不做保留，每一步的最优解一定包含上一步的最优解。

动态规划的全局最优解中一定包含某个局部最优解，但不一定包含前一个局部最优解，因此需要记录之前的所有最优解。

动态规划算法通常以自底向上的方式解各子问题，而贪心算法则通常自顶向下的方式进行。
复习了增强for的概念和使用，在之后的遍历中，应该去自己试着使用一下，现在看懂没问题，但是使用还不够熟练
第一次接近完全实现一次代码，虽然没有AC，超时了，但对于暴力法以及代码调试更加熟练了
将分治算法与递归进行了一个区分理解：一个是不断调用自身，一个是将大问题分成小问题，子问题足够小则直接解决，分而治之，在分治中我看到也用到了递归调用的存在，不过递归只是整个分治中的一部分。
还复习了Math类的max方法，自己使用的时候就没有想到，而是只会用if语句去判断。
个人对于暴力循环也有了一个感悟，应该先将大循环做出来，再去考虑细枝末节的判断，而不是先做一堆判断，再来做剩下的大循环，很有可能你的很多判断在大循环中直接就实现了，而导致冗余，时间复杂度太高。

5、爬楼梯（迭代，递归，动态规划，数学）

1.问题描述

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

2.示例

示例 1：

输入：n = 2
输出：2
解释：有两种方法可以爬到楼顶。
1
2
3

1 阶 + 1 阶
2 阶

示例 2：

输入：n = 3
输出：3
解释：有三种方法可以爬到楼顶。
1
2
3

1 阶 + 1 阶 + 1 阶
1 阶 + 2 阶
2 阶 + 1 阶

3.提示

1 <= n <= 45

4.具体解法（动态规划，递归，斐波那契数列，滚动数组，矩阵快速幂，通项公式）

//方法一：迭代
//第n个台阶只能从第n-1或者n-2个上来。
//到第n-1个台阶的走法 + 第n-2个台阶的走法 = 到第n个台阶的走法
//已经知道了第1个和第2个台阶的走法，一路加上去。第1个台阶只有一种上去的方法，第2个台阶有两种
//相当于是从下面一点点往上捋顺
//写上程序发现，这不就是斐波那契数列嘛
/*
public class Solution {
    public int climbStairs(int n) {
        if(n==1||n==2) return n;//台阶数是1或者2的时候，可能性恰恰就是1或2，所以直接返回n即可
        int a = 1,b = 2;//a表示第n-2个台阶的走法，b表示第n-1个台阶的走法,传统迭代
        int count = 0 ;
        for(int i = 3;i<=n;i++){
            count = a+b;
            //向下迭代
            a = b;//下次迭代的第n-2个台阶的走法等于上次迭代n-1个台阶的走法
            b = count;//下次迭代的第n-1个台阶的走法等于上次迭代的第n个台阶走法
        }
        return count;
    }

}
*/

//for循环里可以是只用两个变量，比较巧妙，但是上面的代码更清晰
//b = a + b;
//a = b - a;
//最后return b;即可



//方法二：用dp数组的形式
//虽然会多了一个数组的空间，但是是对于动态规划的练习
//思路：一般看到题目有多少种方案，这种题意思不需要你列出来具体的多少种方案只需要计算有多少种方案，基本上就可以尝试用动态规划算法来解决问题。

//想好用动态规划就想想动态规划五步曲。
//确定dp数组以及下标的含义 定义dp[i]为爬上第 i 级台阶有多少种方案；
//确定状态转移方程 每次只可以爬1或2个台阶所以，爬上当前台阶的方案应该是前面两个状态的方案的和即，dp[i] = dp[i-1] + dp[i-2]。
//初始化状态i=0级开始爬的，我们可以看作只有一种方案，即 dp[0]=1;i=1代表从第0级到第1级也只有一种方案，即爬一级，dp(1)=1。
//其实题目强调了是1 <= n <= 45，所以其实不用从i=0开始，直接从i=1和i=2开始即可
//遍历顺序 由状态转移方程知道dp[i] 是从 dp[i−1] 和 dp[i−2] 转移过来所以从前往后遍历。
//返回值 因为一共计算 n 阶楼梯有多少方案，所以返回dp[n]。
/*
class Solution {
    public int climbStairs(int n) {
        int [] dp=new int [n+1];
        dp[0]=1;
        dp[1]=1;
        for(int i=2;i<=n;i++){
            dp[i]=dp[i-1]+dp[i-2];
        }
        return dp[n];
    }
}
*/

//方法三：递归
//但是会爆出超时
//其实这个递归算法就是典型的斐波那契数列的写法
/*
class Solution {
    public int climbStairs(int n) {
        if(n==1||n==0) return 1;
        else return climbStairs(n-1)+climbStairs(n-2);
    }
}

//优化后的递归算法
//递归解法中存在重复计算，那么我们可以减少重复计算，将计算的结果保存起来，再次有相关计算的时候，直接从缓存中读取。
//应该是climbStairs(n - 1) + climbStairs(n - 2);中，n-1里面要用到n-2，那么将n-2情况的结果存储好，就不用再迭代去计算了
class Solution {
    HashMap<Integer,Integer> map = new HashMap();
    public int climbStairs(int n) {
        if(n == 1) return 1;
        if(n == 2) return 2;

        if(map.containsKey(n)){
            return map.get(n);
        }

        int sum = climbStairs(n - 1) + climbStairs(n - 2);
        map.put(n,sum);

        return sum;
    }
}
 */
 


//方法四：矩阵快速幂（数学能力）
//以上的方法适用于n比较小的情况，在n变大之后，O(n)的时间复杂度也会显得比较慢，我们可以用「矩阵快速幂」的方法来优化这个过程。
//如何想到使用矩阵快速幂？
//如果一个问题可与转化为求解一个矩阵的n次方的形式，那么可以用快速幂来加速计算
//看不懂数学公式，只是放在这里进行补充就好
/*
public class Solution {
    public int climbStairs(int n) {
        int[][] q = {{1, 1}, {1, 0}};
        int[][] res = pow(q, n);
        return res[0][0];
    }

    public int[][] pow(int[][] a, int n) {
        int[][] ret = {{1, 0}, {0, 1}};
        while (n > 0) {
            if ((n & 1) == 1) {
                ret = multiply(ret, a);
            }
            n >>= 1;
            a = multiply(a, a);
        }
        return ret;
    }

    public int[][] multiply(int[][] a, int[][] b) {
        int[][] c = new int[2][2];
        for (int i = 0; i < 2; i++) {
            for (int j = 0; j < 2; j++) {
                c[i][j] = a[i][0] * b[0][j] + a[i][1] * b[1][j];
            }
        }
        return c;
    }
}

 */

//方法五：通项公式
//可以去先分析这个递推方程f(n)=f(n−1)+f(n−2)的通项公式
//具体的推导可以见力扣官网的官方解答，有了通项公式表示f(n)，直接就可以通过n的值来进行计算了
/*
public class Solution {
    public int climbStairs(int n) {
        double sqrt5 = Math.sqrt(5);
        double fibn = Math.pow((1 + sqrt5) / 2, n + 1) - Math.pow((1 - sqrt5) / 2, n + 1);
        return (int) Math.round(fibn / sqrt5);
    }
}
 */
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140

5.收获

递归只是人看的，方便人的直观理解，递归只是数学语言描述。在工程实践中，要么用带有记忆的递归，要么用动态规划
这道题的后面两种解法都是利用数学公式，没有数学理解是不能吸收的，应该重点掌握动态规划的方式
了解到了动态规划的五部曲
- 确定dp数组以及下标的含义
- 确定状态转移方程
- 初始化状态
- 遍历顺序
- 返回值
解决这种问题可以自己先推导推导再分析，从前往后推，或者从后往前推
对于递归也有了新的了解，这道题里，递归会以2的n次方的指数型增长，所以不适合大数据，但是可以递归的优化，通过哈希表来存储已经计算过得的值，避免递归中的重复运算，这种思路也可以借鉴，但是本题最好还是用来学习动态规划最好，学习递归不适合。
还是存在一个疑问的。在climbStairs(n - 1) + climbStairs(n - 2);中，他是会怎么个递归的方式呢，是n-1的一层层已经递归回来了，还是两个同时进行，一层一层的递归呢，这个需要以后再去发现理解，暂时还不清楚。这个结论会对于哈希表存储的调用过程，具体是怎么节省不必要重复时间的理解有很大帮助。

6、买卖股票的最佳时间（贪心，双指针，动态规划）

1.问题描述

给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。

你只能选择某一天买入这只股票，并选择在未来的某一个不同的日子卖出该股票。设计一个算法来计算你所能获取的最大利润。

返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。

2.示例

示例 1：

输入：[7,1,5,3,6,4]
输出：5
解释：在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
            注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格；同时，你不能在买入前卖出股票。
1
2
3
4

示例 2：

输入：prices = [7,6,4,3,1]
输出：0
解释：在这种情况下, 没有交易完成, 所以最大利润为 0。
1
2
3

3.提示

1 <= prices.length <= 10^5
0 <= prices[i] <= 10^4

4.具体解法（暴力解法，动态规划，双指针，贪心算法）

//方法一：暴力循环
//遍历所有的两个数的差值，最大的就是我们要的结果
//自己写的代码，两分钟，很快，能感觉得到自己从几天前看到一道题完全没有思路的状态到现在可以有暴力循环的想法并成功实践
//但目前还有问题，一方面是暴力循环肯定是不足够，太简单了，每道题的特别解答还不够有思路
//             二方面是每次自己写的暴力循环，都不能成功的将最后的那个超大数组给成功完成，总是报错超出时间限制
/*
class Solution {
    public int maxProfit(int[] prices) {
        int maxprice=0;//最后的返回值最大利润
        //第一次循环是让每个数都跟第一个数去做差，找到差值最大的记作maxprice
        //第二次循环是每个数都跟到二个数做差，以此类推
        for(int i=0;i<prices.length;i++){
            for(int j=i;j<prices.length;j++){
                int sum=prices[j]-prices[i];
                if(sum>maxprice){
                    maxprice=sum;
                }
            }
        }
        return maxprice;
    }
}

 */

//上面的方法会超出时间限制，所以想办法改进
//想到如果当前这个数字小于前面的数，是没必要去做差的，因为是亏本的，还不如初始值0，所以将代码改进（自己想的哦，很有成就感）
class Solution {
    public int maxProfit(int[] prices) {
        int maxprice=0;//最后的返回值最大利润
        for(int i=0;i<prices.length;i++){
            for(int j=i;j<prices.length;j++){
                //加上这个判断，只有prices[j],也就是后面的数（卖价）大于前面的数（买价）的时候，才会执行后面的做差和判断
                if(prices[j]<prices[i]){
                    continue; //跳出本次循环，可以省下很多做差的计算和判断，但遍历的内容是不变的，不知道这样会不会节约时间 
                }
                int sum=prices[j]-prices[i];
                if(sum>maxprice){
                    maxprice=sum;
                }
            }
        }
        return maxprice;

    }
}
//对于第一种进行了改进，去掉了负数的那种做差的计算，但是还是不可以满足，说明遍历次数太多是根本原因，而不是多了那些减法计算


//进行了一些调整还是不够，所以继续改进，这次得从遍历次数上入手了
//又想到一种方法，就是我们这个数如果是所有数中的最大值，就没必要去算一遍，但想想还是要遍历先做判断，不合适
//二次回顾这里的时候，想到一个我们可以在第一次遍历的时候存储一下数组中的最大值，后面判断的时候，如果是最大值，那就不做相应的内层循环了，时间复杂度可以降为O(n-1*n),不知道这种方式可不可以，降低了n次，但是会需要更多的判断和一个变量的空间存储
//按着这个思路去试了一下，还是会报超时


//这是官网的暴力遍历，跟我的第一版几乎一样，唯一不同就是边界上差一个值
//但是这个不影响这个代码还是超出时间问题，所以暴力不太行，官方的也不行
/*
public class Solution {
    public int maxProfit(int[] prices) {
        int maxprofit = 0;
        for (int i = 0; i < prices.length - 1; i++) {
            for (int j = i + 1; j < prices.length; j++) {
                int profit = prices[j] - prices[i];
                if (profit > maxprofit) {
                    maxprofit = profit;
                }
            }
        }
        return maxprofit;
    }
}
 */
 
 
 
//方法二：贪心算法，一次遍历
//每次到新的一天获得当天的新价格，我们都会想，如果我是在价格最低的那天买的就好了
//所以我们可以这样，从第一天开始，每一天都做三件事，第一件，计算跟最低价格的差值，第二件，更新最大利润，第三件，更新最低价格（自己捋顺的，但跟代码有区别）
//注意是历史最低值
//按着代码的思路也可以，每一天都先判断今天的值是不是比历史最小值还低，是就更新最小值，不用计算，不是就进行做差，并判断是不是最大利润并更新
//这个做法也可以理解为贪心算法：我们买卖股票的时候自然会想到在股价最低时购入股票，然后在之后股价最高的一天卖出
//所以我们可以通过一个变量来记录最低股价 同时找到之后股价最高的一天 如此作差就是最大利润
/*
public class Solution {
    public int maxProfit(int prices[]) {
        //这个语句的写法也可以学会，对自己之前写那个最大子数组和用-999进行一个改进
        //因为这个变量是存最小值，所以我们初始给他赋值可能的最小值，避免所有值都比我们给的初始值低（比如给了0）
        int minprice = Integer.MAX_VALUE;                           
        int maxprofit = 0;//最大利润
        for (int i = 0; i < prices.length; i++) {
            if (prices[i] < minprice) {
                minprice = prices[i];//更新历史最小值
            } 
            else if (prices[i] - minprice > maxprofit) {
                //如果今天不是最小值，那么就计算今天跟历史最小值的差值，并比较跟最大利润的值，大的作为新的最大利润
                maxprofit = prices[i] - minprice;
            }
        }
        return maxprofit;
    }
}
*/
 
 
 
//方法三：一个双指针的思想
//其实你仔细捋顺一下这个代码的执行过程，会发现，跟贪心一样
//只不过这个代码是用left存最低价格，用right往后走进行遍历。当right是历史最低，就把left更新成当前right的值，然后继续
//所以代码的写法真的很多种，本质可能一样
/*
class Solution {
    public int maxProfit(int[] prices) {
        if (prices.length <= 1) {
            return 0;
        }
        int left = 0;
        int right = 1;
        int max = 0;
        while (right < prices.length) {
            if (prices[left] <= prices[right]) {
                max = Math.max(max, prices[right] - prices[left]);
                right++;
            } else {
                left = right;
                right = left + 1;
            }
        }
        return max;
    }
}
*/


//方法四：动态规划
    /**
     动态规划解法
     1.定义
     dp[i][j] j=0/1 表示是否持有股票的状态
     dp[i][0]表示第i天未持股下的最大利润 dp[i][1]表示第i天持股下的最大利润
     
     2.状态转移方程
     分持股状态进行讨论
     第i天未持股
     第i-1天也未持股 dp[i][0] = dp[i-1][0] 继承上一天的值
     第i-1天持股 那么第i天是将股票卖出了 dp[i][0] = dp[i-1][1] + price[i]
     对上述情况取最大值
     
     第i天持股
     第i-1天未持股 说明是第i天买入股票的 dp[i][1] = -price[i]
     第i-1天持股 dp[i][1] = dp[i-1][1] 继承上一天的值即可
     对上述情况取最大值
     
     3.初始化
     第1天未买入股票 dp[0][0] = 0
     第1天买入股票 dp[0][1] = -price[0]
     
     4.遍历顺序
     从前往后遍历即可
     */
/*   
class Solution {
    public int maxProfit(int[] prices) {
        int n = prices.length;
        int[][] dp = new int[n][2];
        //base case
        dp[0][0] = 0;
        dp[0][1] = -prices[0];
        for(int i=1;i<n;i++) {
            dp[i][0] = Math.max(dp[i-1][0],dp[i-1][1]+prices[i]);
            dp[i][1] = Math.max(-prices[i],dp[i-1][1]);
        }
        return dp[n-1][0];
    }
}

  */

//另一种状态定义方法：将第i天卖出股票可以获得的最大利润定义为dp[i]，然后求解
/*
class Solution {
    public int maxProfit(int[] prices) {
        int len = prices.length;
        int res = 0;
        // 前一天卖出可以获得的最大利润
        int pre = 0;
        for (int i = 1; i < len; i++) {
            // 利润差
            int diff = prices[i] - prices[i - 1];
           // 状态转移方程：第i天卖出可以获得的最大利润 = 第i-1天卖出的最大利润 + 利润差
            pre = Math.max(pre + diff, 0);
            res = Math.max(res, pre);
        }
        return res;
    }
}
*/
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197

5.收获

暴力循环的超时与否，与每次循环内操作的内容关系不大，关键是在于循环的次数上
掌握了 Integer.MAX_VALUE 的使用，不用自己再去随便设定值了。
动态规划问题的问法：只问最优解，不问具体的解；

题目只问最大利润，没有问这几天具体哪一天买、哪一天卖，因此可以考虑使用 动态规划 的方法来解决；

动态规划用于求解 多阶段决策问题 。
DP的思路：利用原问题与子问题的关系，将其变成大问题的解 = 小问题的解的函数，从而将问题变成size的扩展即可，当size到达最大后，原问题解决了
掌握 无后效性 解决动态规划问题：把约束条件设置成为状态。

买卖股票有约束，根据题目意思，有以下两个约束条件：

条件 1：你不能在买入股票前卖出股票；
条件 2：最多只允许完成一笔交易。
因此当天是否持股是一个很重要的因素，而当前是否持股和昨天是否持股有关系，为此我们需要把是否持股设计到状态数组中。
动态规划的题目，当有约束条件时，要把数组再开一维，作为约束，便于分析。当有约束条件时，一定要把每一个约束条件搞懂，并根据这些约束条件，自己定义出一个约束状态出来，作为新开的那一维数组。
这道题其实非常像那道最大子数组和，唯一的区别是那个是一段，这个两个值的差

7、二叉树的中序遍历（Morris中序遍历，递归，迭代）

1.问题描述

给定一个二叉树的根节点 root ，返回它的中序遍历。

2.示例

示例 1：

输入：root = [1,null,2,3]
输出：[1,3,2]
1
2

示例 2：

输入：root = []
输出：[]
1
2

示例 3：

输入：root = [1]
输出：[1]
1
2

3.提示

树中节点数目在范围 [0, 100] 内
-100 <= Node.val <= 100

4.进阶

递归算法很简单，你可以通过迭代算法完成吗？

5.具体解法（递归，迭代，Morris 中序遍历）

//方法一：递归
//因为要返回一个遍历的结果，那么得要一个存储的容器，我们选择了ArrayList（不限长度，内容用泛型确定为Integer类型），示例的输出就是一个集合
//采用递归的方法，就得有一个方法去被递归，inorder，参数是结点和存储遍历内容的集合
//中序遍历是左，根，右，从根节点出发，如果根节点有左结点，就应该递归调用这个左子树的情况，直到这个此时迭代到的结点没有左子结点，把它存入集合中
//存完了之后，再看这个根节点的右子结点情况如何，不断迭代就可以了
/*
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> res=new ArrayList<>();
        inorder(root,res);
        rerurn res;
    }
    public void inorder(TreeNode root,List<Integer>res){
        if(root==null){
            return;//这个return的效果就是，如果根节点为空，那么就应该不进行下面的操作，返回上一层方法调用
        }
        inorder(root.left,res);
        res.add(root.val);
        inorder(root.right,res);
    }
}
*/



//方法二：迭代
//迭代就不用方法去递归调用了，而是用一个栈去实现
//递归实现时，是函数自己调用自己，一层层的嵌套下去，操作系统/虚拟机自动帮我们用 栈 来保存了每个调用的函数，现在我们需要自己模拟这样的调用过程。
/*
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<Integer>();
        Deque<TreeNode> stk = new LinkedList<TreeNode>();//创建一个栈
        while (root != null || !stk.isEmpty()) {//当根节点不为空或者栈不为空的时候，我们就应该去判断，如果是根节点不为空，那就往左子结点走
            while (root != null) {//直到左子结点是空了，就退出此while
                stk.push(root);
                root = root.left;
            }
            root = stk.pop();//将栈中最后存的那个结点取出，他就是整个树最左下角的结点，值放入集合中
            res.add(root.val);
            root = root.right;//然后将这个root变成右结点再去看对应这个层的右子树情况
        }
        return res;
    }
}
*/



//方法三：Morris中序遍历
//用递归和迭代的方式都使用了辅助的空间，而莫里斯遍历的优点是没有使用任何辅助空间。
//缺点是改变了整个树的结构，强行把一棵二叉树改成一段链表结构。


//Morris 遍历算法整体步骤如下（假设当前遍历到的节点为 x）：
//如果x无左孩子，先将x的值加入答案数组，再访问x的右孩子，即x=x.right。
//如果x有左孩子，则找到x左子树上最右的节点（即左子树中序遍历的最后一个节点，x在中序遍历中的前驱节点），我们记为predecessor。
//根据predecessor的右孩子是否为空，进行如下操作：
//如果predecessor的右孩子为空，则将其右孩子指向x，然后访问x的左孩子，即x=x.left。
//如果predecessor的右孩子不为空，则此时其右孩子指向x，说明我们已经遍历完x的左子树，我们将predecessor的右孩子置空，将x的值加入答案数组，然后访问x的右孩子，即 x=x.right。
//重复上述操作，直至访问完整棵树。

//其实整个过程我们就多做一步：假设当前遍历到的节点为x，将x的左子树中最右边的节点的右孩子指向x，
//这样在左子树遍历完成后我们通过这个指向走回了x，且能通过这个指向知晓我们已经遍历完成了左子树，而不用再通过栈来维护，省去了栈的空间复杂度。
/*
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<Integer>();
        TreeNode predecessor = null;

        while (root != null) {
            if (root.left != null) {
                // predecessor节点 就是当前 root 节点向左走一步，然后一直向右走至无法走为止
                predecessor = root.left;
                while (predecessor.right != null && predecessor.right ! = root) {
                    predecessor = predecessor.right;
                }

                // 让 predecessor 的右指针指向 root，继续遍历左子树
                if (predecessor.right == null) {
                    predecessor.right = root;
                    root = root.left;
                }
                // 说明左子树已经访问完了，我们需要断开链接
                else {
                    res.add(root.val);
                    predecessor.right = null;//这个就把强加过来的链接断开了
                    root = root.right;
                }
            }
            //如果没有左孩子，则直接访问右孩子
            else {
                res.add(root.val);
                root = root.right;
            }
        }
        return res;
    }
}
*/
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100

对于方法三的一个补充理解：

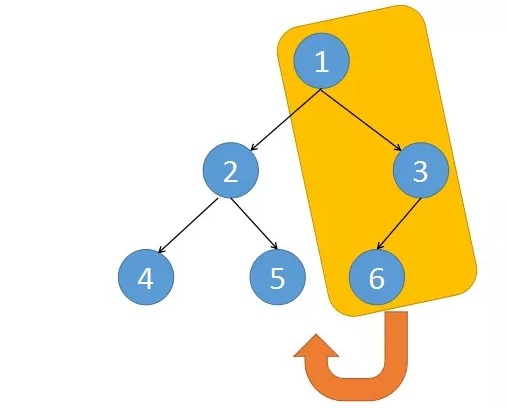
我们将黄色区域部分挂到节点5的右子树上，接着再把2和5这两个节点挂到4节点的右边。
这样整棵树基本上就变改成了一个链表了，之后再不断往右遍历。

只要当前结点有左子节点，我们就把此结点和右子树都挂到左子结点的右下角，以此类推挂完了之后，再去遍历

而且遍历完每个左子树的时候，都要断开之前的一个挂的链接，恢复之前的形状

6.收获

二叉树的递归迭代遍历代码是非常重要的，他的层层迭代很抽象
遍历这种问题，都需要有一个返回值，这个时候得想用什么存储，这个是需要自己想到的
递归的话，就得写一个方法去递归，而且得有出口
定义 inorder(root) 表示当前遍历到root 节点的答案，那么按照定义，我们只要递归调用 inorder(root.left) 来遍历 root 节点的左子树，然后将 root 节点的值加入答案，再递归调用inorder(root.right) 来遍历 root 节点的右子树即可，递归终止的条件为碰到空节点。（中序遍历的思路）
前序遍历：打印 - 左 - 右
中序遍历：左 - 打印 - 右
后序遍历：左 - 右 - 打印
题目要求的是中序遍历，那就按照左-打印-右这种顺序遍历树就可以了，递归函数实现

终止条件：当前节点为空时
函数内：递归的调用左节点，打印当前节点，再递归调用右节点
对于树、链表等有了新认识，就是树，链表等这种数据结构，我们在实现的时候是通过一个类来实现的，里面有（以树为例）值，左节点，右节点，还有构造方法，这样其实是一个结点，而通过一个又一个结点，这样组成了我们想表达的树，在使用的时候也是利用这几个成员变量去分析。

8、对称二叉树（递归，迭代）

1.问题描述

给你一个二叉树的根节点 root ，检查它是否轴对称。

2.示例

示例 1：

输入：root = [1,2,2,3,4,4,3]
输出：true
1
2

示例 2：

输入：root = [1,2,2,null,3,null,3]
输出：false
1
2

3.提示

树中节点数目在范围 [1, 1000] 内
-100 <= Node.val <= 100

4.进阶

你可以运用递归和迭代两种方法解决这个问题吗？

5.具体解法（递归，迭代）

//方法一：递归
//判断一个二叉树是否对称只需要去看他的左子树和右子树是否相等，进而找到了递归的方向
//我们可以实现这样一个递归函数，通过「同步移动」两个指针的方法来遍历这棵树，
//p指针和q指针一开始都指向这棵树的根，随后p右移时，q左移，p左移时，q右移。每次检查当前p和q节点的值是否相等，如果相等再判断左右子树是否对称。判断左右子树就是一种递归，注意是p.left和q.right去做比较

/*
class Solution {
    public boolean isSymmetric(TreeNode root) {
        return check(root, root);
    }

    public boolean check(TreeNode p, TreeNode q) {
        if (p == null && q == null) {
            return true;
        }
        if (p == null || q == null) {
            return false;
        }
        return p.val == q.val && check(p.left, q.right) && check(p.right, q.left);
    }
}
*/
 


//方法二：迭代
//那么如何用迭代的方法实现呢？首先我们引入一个队列，这是把递归程序改写成迭代程序的常用方法。
//初始化时我们把根节点入队两次。
//每次提取两个结点并比较它们的值（队列中每两个连续的结点应该是相等的，而且它们的子树互为镜像），
//然后将两个结点的左右子结点按相反的顺序插入队列中。
//当队列为空时，或者我们检测到树不对称（即从队列中取出两个不相等的连续结点）时，该算法结束。
/*
class Solution {
    public boolean isSymmetric(TreeNode root) {
        return check(root, root);
    }

    public boolean check(TreeNode u, TreeNode v) {//这个方法同时操作两个结点
        Queue<TreeNode> q = new LinkedList<TreeNode>();
        q.offer(u);
        q.offer(v);//因为第一次uv都是root，所以根节点是进去两次
                   //offer()方法的作用是：如果在不违反容量限制的情况下立即执行，则将指定的元素插入到此队列中。 
        while (!q.isEmpty()) {
            u = q.poll();
            v = q.poll();//队列不为空的情况下，将队列中的值拿出来作比较
            if (u == null && v == null) {
                continue;//两个点都是空，那么不做比较直接
            }
            if ((u == null || v == null) || (u.val != v.val)) {
                return false;//如果其中一个结点是空，或者值不相同（不存在同时为空，前面判断过了），那么就说明不对称，返回false
            }
            //如果前面满足，说明对称，那么我们就往下继续判断他们的子节点，按照u.left，v.right，u.right，v.left的顺序放入，
            //这样取的时候是两两挨着取出来作比较的
            q.offer(u.left);
            q.offer(v.right);

            q.offer(u.right);
            q.offer(v.left);
        }
        //当队列为空的那一步执行到这里，说明是对称的，中间没有问题，返回true
        return true;
    }
}
*/

//上面的迭代方法，第一次是将两个根节点放进去，这样就多了一次迭代
//其实可以不去判断根节点，直接判断他的两个子树就好，但是要加上一个根节点为空的判断不为空才继续进行
//题目其实直接给了结点数目为1到1000，所以其实可以不用判断根节点为空的，
// 直接将代码q.offer(u);
//         q.offer(v);改作q.offer(root.left);
//                       q.offer(root.right);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71

6.收获

直接中序遍历，比较数组是否对称可行吗？不可行，比如[1,2,2,2,null,2]这个中序遍历后是[2,2,1,2,2]但是树不对称。有个大哥给了一个想法，是对null做特殊操作，把这个null都改成层数的负值，虽然可能会跟对应的val同值，但是对付测试用例他成功了，所以处理好结点为空的情况，还是有使用中序遍历的可能的
迭代一般都可以与递归互相切换，但是不一定哪个更加的简洁
引入队列或者栈的方式，是将递归改成迭代的一种常见思路，递归其实隐藏了一个栈或队列，来存储一些递归的信息，所以我们自己用栈或队列来模拟这种过程
感觉这些题目除了基本的处理思路之外，就是要多结合树啊，链表，队列等结构进行处理，最好可以先自己用思路捋顺，然后再用数据结构去实现
这题跟100题判断两棵树是否相同很相似，对称与相等的区别我觉得也就是进入下一层递归时，两棵子树A、B的左右子树顺序换一下就行了

9、二叉树的最大深度（BFS，DFS）

1.问题描述

给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明: 叶子节点是指没有子节点的节点。

2.示例
给定二叉树 [3,9,20,null,null,15,7]，

返回它的最大深度 3 。

3.具体解法（深度优先搜索，广度优先搜索）

//方法一：深度优先搜索
//如果我们知道了左子树和右子树的最大深度 l 和 r，那么该二叉树的最大深度即为max(l,r)+1
//而左子树和右子树的最大深度又可以以同样的方式进行计算。
//因此我们可以用「深度优先搜索」的方法来计算二叉树的最大深度。
//具体而言，在计算当前二叉树的最大深度时，可以先递归计算出其左子树和右子树的最大深度
//然后在O(1)时间内计算出当前二叉树的最大深度。递归在访问到空节点时退出。

/*
class Solution {
    public int maxDepth(TreeNode root) {
        if (root == null) {
            return 0;
        } else {
            int leftHeight = maxDepth(root.left);
            int rightHeight = maxDepth(root.right);
            return Math.max(leftHeight, rightHeight) + 1;
        }
    }
}
*/


//方法二：广度优先搜索
//我们也可以用「广度优先搜索」的方法来解决这道题目，但我们需要对其进行一些修改，
//此时我们广度优先搜索的队列里存放的是「当前层的所有节点」。
//每次拓展下一层的时候，不同于广度优先搜索的每次只从队列里拿出一个节点，我们需要将队列里的所有节点都拿出来进行拓展，
//这样能保证每次拓展完的时候队列里存放的是当前层的所有节点，即我们是一层一层地进行拓展，
//最后我们用一个变量ans来维护拓展的次数，该二叉树的最大深度即为ans。

//利用了队列中一层全部出队列，另一层会完全装进来。巧妙的利用了队列长度size来控制一层完全出队。
//自己理解就是先将根节点放进队列，
//然后看队列是不是为空，如果不为空，就出队列，
//然后再将所有的子节点进队列，并用一个depth变量记录，不断重复，直到队列为空（也就是都没子节点了，所以遍历到了最后一层了）
/*
class Solution {
    public int maxDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }
        Queue<TreeNode> queue = new LinkedList<TreeNode>();
        queue.offer(root);
        int ans = 0;
        while (!queue.isEmpty()) {
            int size = queue.size();
            while (size > 0) {
                TreeNode node = queue.poll();
                if (node.left != null) {
                    queue.offer(node.left);
                }
                if (node.right != null) {
                    queue.offer(node.right);
                }
                size--;//每次外层while重新进来，队列里存储的只是本层的元素，size是他们的多少，
                       //而在内层while的时候会加入下一层节点，size递减为0的时候代表本层结束了，本层结束代表ans要加一，
                       //此时queue里面存储的只有下一层的节点，再次重新循环。
                       //也就是说每外层while一次代表一层节点遍历完毕，ans就加一。
            }
            ans++;
        }
        return ans;
    }
}
 */
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63

4.收获

非递归版的层次遍历用的则是队列，这是由于层次遍历的属性非常契合队列的特点。所以用队列不用栈
学习到了二叉树的广度优先遍历和深度优先遍历
层次遍历的关键在于，要把当前一层的所有node 都遍历完，才能增加深度值
感觉这两种遍历都是依托于递归的，都是用递归来实现的

10、只出现一次的数字（哈希表，异或）

1.问题描述

给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。

说明：

你的算法应该具有线性时间复杂度。你可以不使用额外空间来实现吗？

2.示例

示例 1:

输入: [2,2,1]
输出: 1
1
2

示例 2:

输入: [4,1,2,1,2]
输出: 4
1
2

3.具体解法（哈希表，集合，求和方法，异或）

//方法一：自己想的遍历法，但是想错了，写成了找出重复的数字，不过过程中锻炼了自己的思维，还强化了哈希表的创建过程
//对于哈希表的使用开始有思路了，但是这道题用哈希表可能有点浪费，但是为了用它的containsKey方法，所以我把键和值都存同样的
//其实这样感觉用一个数组或者链表就可以了，而我们是为了查询使用，所以应该是数组，但是数组有没有类似containsKey的方法，我不知道，所以只能用哈希表了
/*
class Solution {
    public int singleNumber(int[] nums) {
        Map<Integer,Integer> hs=new HashMap<>();
        for(int i=0;i<nums.length;i++){
            if(hs.containsKey(nums[i])){//如果哈希表里有当前遍历到的数字，就返回这个数字
                return nums[i];
            }
            else{
                hs.put(nums[i],nums[i]);//没有就存入哈希表
            }
        }
        //这里要求我必须有一个返回值，没办法写了return;，但是会报错，所以只能写了个返回-1
        //为什么非要一个返回值呢，明明我在for循环那里已经写了返回值，原因应该是else不一定能执行到，虽然我们知道案例里肯定有
        //所以对于这种情况的处理要有所掌握
        return -1;
    }
}
*/


//随后我进行了思路的改进
//当哈希表中有这个元素的时候，就把这个元素移除，没有就存进去，这样的话，就可以最后只剩下一个没重复的元素在哈希表里
//但我取不出来，因为最后我试图找到一个方法返回哈希表的最后一个元素，但是没有，我试着return hs;会报错
//想到这个应该是哈希表的遍历的内容了，我可以遍历哈希表，最后返回就可以了，但哈希表的遍历我还没掌握
//水平到这里了，目前没法将这个代码成功实现，得换个东西来实现或者掌握哈希表的遍历
/*
class Solution {
    public int singleNumber(int[] nums) {
        Map<Integer,Integer> hs=new HashMap<>();
        for(int i=0;i<nums.length;i++){
            if(hs.containsKey(nums[i])){
                hs.remove(nums[i]);
            }
            else{
                hs.put(nums[i],nums[i]);
            }
        }
        return hs;
    }
}
*/


//二次回顾，已经掌握了哈希表的遍历，并且把这个代码给实现了
/*
class Solution {
    public int singleNumber(int[] nums) {
        Map<Integer,Integer> hs=new HashMap<>();
        for(int i=0;i<nums.length;i++){
            if(hs.containsKey(nums[i])){
                hs.remove(nums[i]);
            }
            else{
                hs.put(nums[i],nums[i]);
            }
        }
        //keySet()：返回此地图中包含的键的Set视图。
        Set<Integer> set =hs.keySet();
        //得到遍历 key 的选代器
		Iterator it = set.iterator();
        Integer key=0;//这个是存储每一次循环时输出的值，这里写int key=0;也是可以的		
		while(it.hasNext()){
			key=(Integer) it.next();//这里必须进行强转
            return key;//因为我知道哈希表最后只会有一个数，所以只会执行一次
        }
        return key;//非要我在这去输出一个值，我根本用不到这里的输出
    }
}
*/

//方法二：使用哈希表存储每个数字和该数字出现的次数。
//附上另一个使用哈希表成功的算法
//不过这个哈希表的使用跟我的想法是不一样的，我的是有就移除，没有就进表，之后只剩一个元素，肯定是我要的那个，遍历返回
//这个方法是遇到一次就会给value加1，随后遍历哈希表，如果value是2，那就没操作继续往后找，如果value是1，那就返回其键值
/*
class Solution {
    public int singleNumber(int[] nums) {
        Map<Integer, Integer> map = new HashMap<>();
        for (Integer i : nums) {
            Integer count = map.get(i);//获得数字这个值在哈希表中的键值对，也就是这个值对应的次数
            count = count == null ? 1 : ++count;//看次数是不是存在，也就是是不是存储过，没存过就记为1，存过就++
            map.put(i, count);
        }
        for (Integer i : map.keySet()) {
            Integer count = map.get(i);
            if (count == 1) {
                return i;//遍历键，找到值是1，的返回其键值；
            }
        }
        return -1;
    }
}
*/

//方法三：使用集合存储数组中出现的所有数字，并计算数组中的元素之和。
//由于集合保证元素无重复，因此计算集合中的所有元素之和的两倍，即为每个元素出现两次的情况下的元素之和。
//由于数组中只有一个元素出现一次，其余元素都出现两次，因此用集合中的元素之和的两倍减去数组中的元素之和，剩下的数就是数组中只出现一次的数字。
//下面的代码是我根据思路自己写出来的
/*
class Solution {
    public int singleNumber(int[] nums) {
        Set <Integer> set=new HashSet<>();
        int numssum=0;//数组的值的总和
        int setsum=0;//集合的数值总和
        for(int i=0;i<nums.length;i++){
            numssum=numssum+nums[i];
            set.add(nums[i]);
        }
        Iterator it = set.iterator();
        while(it.hasNext()){
            int k=(Integer) it.next();//这里必须进行强转
			setsum=setsum+k;
        }
        return setsum*2-numssum;
    }
}
*/



//方法四：位运算
//上述三种解法都需要额外使用O(n)的空间，其中n是数组长度。
//如何才能做到线性时间复杂度和常数空间复杂度呢？
//答案是使用位运算。对于这道题，可使用异或运算⊕。

//任何数和0做异或运算，结果仍然是原来的数
//任何数和其自身做异或运算，结果是0
//异或运算满足交换律和结合律
//根据上面的三个性质可以发现，数组中的全部元素的异或运算结果即为数组中只出现一次的数字。
/*
class Solution {
    public int singleNumber(int[] nums) {
        int single = 0;
        for (int num : nums) {
            single ^= num;
        }
        return single;
    }
}
*/
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144

4.收获

掌握了哈希表的遍历方式，通过用两个方法keySet()和entrySet()去返回一个Set集合，并结合Set集合的遍历来遍历哈希表
同时也复习的Set集合的遍历方式之一：创建迭代器对象 Iterator it = set.iterator();
了解了Set和Map的区别，一个是不能存储重复元素，一个是存储键值对。
对于必须有一个返回值，但是又不知道怎么去在最后面的位置去写一个return，我想到的是return -1；以后应该会能学习到更好的处理方法
这个题目如果是其他的都是未知次（不等于1），这个时候用哈希表是非常好的，可以存储数字出现的次数
学会了位运算的思路，并且学习到了异或的三个特性

//任何数和0做异或运算，结果仍然是原来的数
//任何数和其自身做异或运算，结果是0
//异或运算满足交换律和结合律
数组中的全部元素的异或运算结果即为数组中只出现一次的数字。
“异或”用人话来说就是“找不同”，比如两幅图找不同，不同的点才为true，相同的部分为false。

11、移动零（双指针）

1.问题描述

给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序。

请注意，必须在不复制数组的情况下原地对数组进行操作。

2.示例

示例 1:

输入: nums = [0,1,0,3,12]
输出: [1,3,12,0,0]
1
2

示例 2:

输入: nums = [0]
输出: [0]
1
2

3.提示

1 <= nums.length <= 104
-2^31 <= nums[i] <= 2^31 - 1

4.进阶

你能尽量减少完成的操作次数吗？

5.具体解法（新容器存储，覆盖补0，双指针）

//方法一：自己想到，可以先遍历一遍数组，用另一个容器把所有的非零数都存起来，遇到零就记个数，最后再从容器后面填上零
//容器可以选择另一个数组，但是要求说在不复制数组的情况下，原地对数组进行操作，我这种想法应该是不可以了

//方法二：不用新容器，采用覆盖后面补0的形式
//其实这个也是一种双指针的方式
//与后面的方法三区别在于，方法三是直接交换零和非零元素，最后就不用再做补零
//而这个方法是将非零数去覆盖前面的0，然后再将剩下的都赋值为0
/*
class Solution {
    public void moveZeroes(int[] nums) {
        int indexNow = 0;//这个是计0的个数的，遇到非零的时候他才往后走一个，最后他的位置是在中间，然后从他开始遍历赋值0
        int indexNum = 0;//这个是一直往后走的
        int m = nums.length;

        while(indexNum<m){
            if(nums[indexNum] != 0) {
                //其实这句的感觉就像是新建了一个数组一样，不等于零的时候才会有赋值和indexNow++
                nums[indexNow++] = nums[indexNum];
            }
            ++indexNum;//无论这个数等不等于0，都会将这个指针往后移动
        }
        
        //这个是后面补零的部分
        for(int i = indexNow; i < m; i++){
            nums[i] = 0;
        }
    }
}
*/


//方法三：双指针
//使用双指针，左指针指向当前已经处理好的序列的尾部，右指针指向待处理序列的头部。右指针不断向右移动，每次右指针指向非零数，则将左右指针对应的数交换，同时左指针右移。
//上面这句话可以理解为，左右一起走，遇到非零都往后走，遇到0，左就停下来，右继续走，知道遇到新的非零，这个时候将左处的零换成右处的非零数。然后左可以往右移动一位（注意是一位，而不是移动到右的位置），然后继续前进，其实右与左之间的距离就是零的个数，最后右走完了，把所有非零的都挪到前面了
//注意到以下性质：
//左指针左边均为非零数；
//右指针左边直到左指针处均为零。
//因此每次交换，都是将左指针的零与右指针的非零数交换，且非零数的相对顺序并未改变。
/*
class Solution {
    public void moveZeroes(int[] nums) {
        int n = nums.length, left = 0, right = 0;
        while (right < n) {
            if (nums[right] != 0) {
                swap(nums, left, right);
                left++;
            }
            right++;
        }
    }

    public void swap(int[] nums, int left, int right) {
        int temp = nums[left];
        nums[left] = nums[right];
        nums[right] = temp;
    }
}
*/
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58

6.收获

掌握了双指针的方法，这种类似的有标记的事情都可以用双指针来做
锻炼了对于数组的操作能力

12、多数元素（哈希表，排序，随机化，分治）

1.问题描述

给定一个大小为 n 的数组，找到其中的多数元素。多数元素是指在数组中出现次数大于 ⌊ n/2 ⌋ 的元素。

你可以假设数组是非空的，并且给定的数组总是存在多数元素。

2.示例

示例 1：

输入：[3,2,3]
输出：3
1
2

示例 2：

输入：[2,2,1,1,1,2,2]
输出：2
1
2

3.进阶

尝试设计时间复杂度为 O(n)、空间复杂度为 O(1) 的算法解决此问题。

4.具体解法（哈希表，排序，分治，随机化，Boyer-Moore 投票算法）

//方法一：使用哈希表存储值和出现次数
//拿到题目想到的就是这道题可以使用之前的《只出现一次的数字》这道题目中使用的哈希表方式
//通过遍历数组，同时用哈希表存储出现的数值和其出现的次数，然后遍历结束之后再遍历哈希表，找到最大的次数值，返回其对应的键值
//但是我自己写的这个代码的时间复杂度和空间复杂度都很高
/*
class Solution {
    public int majorityElement(int[] nums) {
        Map<Integer,Integer> hs=new HashMap<>();
        int max=0;//用来存储后面遍历哈希表时的临时最大次数
        int res=0;//用来存储对应临时最大次数的键值，最后结果也是他
        for (Integer i : nums) {//增强for遍历数组
            Integer count = hs.get(i);
            //注意理解好这句话，判断count == null吗，等于则 count =1，不为空就count+1
            count = count == null ? 1 : ++count;
            hs.put(i, count);
        }
        for (Integer i : hs.keySet()) {//增强for遍历哈希表
            Integer count = hs.get(i);
            if (count > max) {
                max=count;
                res=i;
            }
        }
        return res;
    }
}
 */



//方法二：排序
//排完序其实可以想到，不论如何，二分之n处的值一定是属于最大出现次数的那个（因为题干强调他们会出现大于一半的次数）
//所以我们只需要返回排序后的数组中的第二分之n处的值即可
//如果使用语言自带的排序算法，需要使用O(logn)的栈空间。如果自己编写堆排序，则只需要使用O(1)的额外空间。而哈希表的时间和空间复杂度都是O(n)
/*
class Solution {
    public int majorityElement(int[] nums) {
        Arrays.sort(nums);//数组自带的排序方法（Arrays类，包含用于操作数组的各种方法，不用导包就可以使用）
        return nums[nums.length/2];
    }
}
*/



//方法三：随机化
//因为超过二分之n的数组下标被众数占据了，这样我们随机挑选一个下标对应的元素并验证，有很大的概率能找到众数。
//这个方法的时间复杂度理论上来书是O（∞），因为有可能永远也随机不到那个众数
//但我们可以算期望，以恰好是二分之一为例，期望的次数和是2，每一次随机后要用O（n）的时间去查个数，所以期望的时间复杂度为O(n)
/*
class Solution {
      
    //nextInt(int bound)返回伪随机数，从0（包括）和指定值（排除）之间均匀分布的int值，从该随机数生成器的序列中抽取出来。
    //得创建一个Random类的对象，才能使用这个产生随机数的方法 
    private int randRange(Random rand, int min, int max) {
        return rand.nextInt(max - min) + min;
    }
    
    //这个方法就是给一个数和数组去统计数组中这个数字的个数并返回个数
    private int countOccurences(int[] nums, int num) {
        int count = 0;
        for (int i = 0; i < nums.length; i++) {
            if (nums[i] == num) {
                count++;
            }
        }
        return count;
    }

    public int majorityElement(int[] nums) {
        Random rand = new Random(); //得创建一个Random类的对象，才能使用这个产生随机数的

        int majorityCount = nums.length/2;//如果测试的那个数的次数大于数组长度的一半，就是众数

        while (true) {
            int candidate = nums[randRange(rand, 0, nums.length)];
            if (countOccurences(nums, candidate) > majorityCount) {//是众数说明就是我们要找的那个数
                return candidate;
            }
        }
    }
}
*/



//方法四：分治
//如果a是nums的众数，那将nums分成两组，则a至少是其中一个组中的众数（可以用反证法证明，如果都不是，那a也不是nums数组的众数了）
//这样可以将nums一分为二用分治的方法进行处理
//我们使用经典的分治算法递归求解，直到所有的子问题都是长度为 1 的数组。
//长度为1的子数组中唯一的数显然是众数，直接返回即可。
//如果回溯后某区间的长度大于 1，我们必须将左右子区间的值合并。
//如果它们的众数相同，那么显然这一段区间的众数是它们相同的值。
//否则，我们需要比较两个众数在整个区间内出现的次数来决定该区间的众数。
/*
class Solution {
    //这个是在lo到hi之间对nums数组去查num的个数
    private int countInRange(int[] nums, int num, int lo, int hi) {
        int count = 0;
        for (int i = lo; i <= hi; i++) {
            if (nums[i] == num) {
                count++;
            }
        }
        return count;
    }

    private int majorityElementRec(int[] nums, int lo, int hi) {
        //如果头和尾直接一样的角标，那么说明数组只有一个元素了，一个元素的众数就是其对应的值
        if (lo == hi) {
            return nums[lo];
        }

        //对数组进行一个拆分，分别对两段调用这个找众数的方法，直到数组只有一个数的时候，开始逐层返回
        int mid = (hi - lo) / 2 + lo;
        int left = majorityElementRec(nums, lo, mid);
        int right = majorityElementRec(nums, mid + 1, hi);

        //如果左和右区间的众数相同，说明众数就是这个
        if (left == right) {
            return left;
        }

        //如果左区间和右区间的众数不相同，那就去查各自区间的众数具体是几个，然后去比大小
        int leftCount = countInRange(nums, left, lo, hi);
        int rightCount = countInRange(nums, right, lo, hi);

        return leftCount > rightCount ? left : right;
    }
    
    //这个是整个程序的入口，从这里开始执行
    public int majorityElement(int[] nums) {
        return majorityElementRec(nums, 0, nums.length - 1);
    }
}
 */


//方法五：Boyer-Moore 投票算法（时间度复杂度O(n)，空间复杂度O(1)）
//其实理论是不管这个candidate是谁，只有那个众数可以抵住所有人的进攻（不同减一），成为留到最后的那个人，也许他一开始不是candidate，但后面一定会上来

//如果候选人不是m，则m会和其他非候选人一起反对，会反对候选人,所以候选人一定会下台(m==0时发生换届选举)
//如果候选人是m,则m会支持自己，其他候选人会反对，同样因为m票数超过一半，所以m一定会成功当选

/*
class Solution {
    public int majorityElement(int[] nums) {
        int count = 0;
        Integer candidate = null;

        for (int num : nums) {
            if (count == 0) {
                candidate = num;//count等于0，就是那个数被抵消没了，所以将现在遍历到的数作为candidate
            }
            count += (num == candidate) ? 1 : -1;//num是不是等于candidate，是就给count+1，不是就-1
        }

        return candidate;
    }
}
 */
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161

5.收获

Arrays类，包含用于操作数组的各种方法，不用导包就可以使用，复习了 Arrays.sort(nums)的使用
由题意知，众数的个数，至少比其他所有非众数加起来还要多1（也就是众数这个选举人一定有足够多的人支持，他可能在遍历的中途下台，但是最终一定会再次上台，成功当选）
对于分治递归的方法有了理解，其实分治是需要用到递归的，但递归不一定是分治的情况，分治是那种大问题往小问题转换的思路，化成小问题可以一眼看出结论，然后再递归回来，重点是划分与递归回来的设计
在很多数中去找一个东西，可以想到分治的思想，也就是不断细化，直到可以轻松的找到，然后递归返回结果。
藏在管子里的蛇，身体长于管子的一半的话，砍中间就肯定能砍到（排序）
有很多巧妙的解释，都是这些题目去理解的好办法

13、最小栈（栈）

1.问题描述

设计一个支持 push ，pop ，top 操作，并能在常数时间内检索到最小元素的栈。

实现 MinStack 类:

MinStack() 初始化堆栈对象。
void push(int val) 将元素val推入堆栈。
void pop() 删除堆栈顶部的元素。
int top() 获取堆栈顶部的元素。
int getMin() 获取堆栈中的最小元素。

2.示例

示例 1:

输入：
["MinStack","push","push","push","getMin","pop","top","getMin"]
[[],[-2],[0],[-3],[],[],[],[]]

输出：
[null,null,null,null,-3,null,0,-2]

解释：
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin();   --> 返回 -3.
minStack.pop();
minStack.top();      --> 返回 0.
minStack.getMin();   --> 返回 -2.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

3.提示

-2^31 <= val <= 2^31 - 1
pop、top 和 getMin 操作总是在非空栈上调用
push, pop, top, and getMin最多被调用 3 * 10^4 次

4.具体解法（双辅助栈，单辅助栈，链表，差值存储，同步不同步）

//方法一：辅助栈
//对于栈来说，如果一个元素 a 在入栈时，栈里有其它的元素 b, c, d，
//那么无论这个栈在之后经历了什么操作，只要 a 在栈中，b, c, d 就一定在栈中，因为在 a 被弹出之前，b, c, d 不会被弹出。
//因此，在操作过程中的任意一个时刻，只要栈顶的元素是 a，那么我们就可以确定栈里面现在的元素一定是 a, b, c, d
//那么，我们可以在每个元素 a 入栈时把当前栈的最小值 m 存储起来。在这之后无论何时，如果栈顶元素是 a，我们就可以直接返回存储的最小值 m。

//按照上面的思路，我们只需要设计一个数据结构，使得每个元素 a 与其相应的最小值 m 时刻保持一一对应。
//因此我们可以使用一个辅助栈，与元素栈同步插入与删除，用于存储与每个元素对应的最小值。

//当一个元素要入栈时，我们取当前辅助栈的栈顶存储的最小值，与当前元素比较得出最小值，将这个最小值插入辅助栈中；
//当一个元素要出栈时，我们把辅助栈的栈顶元素也一并弹出；
//在任意一个时刻，栈内元素的最小值就存储在辅助栈的栈顶元素中。

//个人总结，只有入栈和出栈的时候，才是两个栈同时操作，如果是获得栈顶元素或者获得当前最小值，就只对那个专属的栈进行操作即可
//这个其实是很对自己有提示的，后面遇到类似的什么最大栈这种问题，都可以用类似的操作去进行
//甚至可以不止两个栈，可以多个栈进行操作，这样可以同时给我们的这个提供好几个功能
/*
class MinStack {
    Deque<Integer> xStack;//数据栈
    Deque<Integer> minStack;//同步栈

    public MinStack() {
        xStack = new LinkedList<Integer>();
        minStack = new LinkedList<Integer>();
        minStack.push(Integer.MAX_VALUE);//栈里最初试存一个int类型可能的最大值，用来后面跟存进来的数字进行比较，存最小值
    }

    public void push(int x) {
        xStack.push(x);
        minStack.push(Math.min(minStack.peek(), x));//执行push操作的时候，会两个栈各自进行操作，一个存数，一个存当前最小值
    }

    public void pop() {
        xStack.pop();
        minStack.pop();//执行pop操作的时候是两个都要同时去出，要不然就不匹配了
    }

    public int top() {
        return xStack.peek();//top是获取堆栈顶部的元素，peek是查看堆顶元素且不删除，正好符合
    }

    public int getMin() {
        return minStack.peek();//要获得当前的最小值，就从minStack这个栈去获得
    }
}
*/



//法二：方法一是用了两个栈，那我们可以用一个栈吗
//如果只用一个栈，结合一个变量去存最小值呢
//问题是遇到新的最小值，会覆盖之前存储的最小值，应该怎么去做
//可以在遇到新的最小值的时候，将之前的最小值压栈，这样栈里是一个值一个最小值，变量存的是最新的最小值
//（补充一下，不是一个值一个最小值，是一些值加最小值，就是最小值都是他的话，就没重新存，他这种属于是不同步的方式）
//（不过其实也可以按着我一个值一个最小值的思路来进行，就是不管你来的是不是更小，只要压栈，我就先压min，再压数，如果min小于数，再更新一下min=数）
//当我们要找最小值时返回变量里的即可，当我们执行一次出栈之后，接着再出一次栈，这个第二个出来的就是此时的最小值，赋值给那个变量即可
/*
class MinStack {
    int min = Integer.MAX_VALUE;
    Stack<Integer> stack = new Stack<Integer>();
    public void push(int x) {
        //当前值更小
        if(x <= min){
            //将之前的最小值保存
            stack.push(min);
            //更新最小值
            min=x;
        }
        stack.push(x);
    }

    public void pop() {
        //如果弹出的值是最小值，那么将下一个元素更新为最小值
        if(stack.pop() == min) {
            min=stack.pop();
        }
    }

    public int top() {
        return stack.peek();
    }

    public int getMin() {
        return min;
    }
}
*/


//方法三：用差值去进行存储
//用了另一种思路。同样是用一个 min 变量保存最小值。
//只不过栈里边我们不去保存原来的值，而是去存储入栈的值和最小值的差值。
//然后得到之前的最小值的话，我们就可以通过 min 值和栈顶元素得到

//再理一下上边的思路，我们每次存入的是 原来值 - 当前最小值。
//当原来值大于等于当前最小值的时候，我们存入的肯定就是非负数，所以出栈的时候就是 栈中的值 + 当前最小值 。
//当原来值小于当前最小值的时候，我们存入的肯定就是负值，此时的值我们不入栈，用 min 保存起来，同时将差值入栈。
//当后续如果出栈元素是负数的时候，那么要出栈的元素其实就是 min。
//此外之前的 min 值，我们可以通过栈顶的值和当前 min 值进行还原，就是用 min 减去栈顶元素即可。
//著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

//自己捋顺一下就是存的时候存原来的值减最小值（栈如果是空的，第一个最小值设为x）
//如果差值是正数，就只存进去就行，要是差值是负数，说明得更新最小值min=x，
//上面是入栈的时候操作，下面是出栈
//出栈的时候，如果出来的是正数，直接min+它就是我要出的
//出来的是负数，那就说明要出栈的就是min，而且此时也得更新min=min-这个出栈的元素

//由于我们保存的是差值，所以可能造成溢出，所以我们用了数据范围更大的 long 类型。

//此外相对于解法二，最小值需要更新的时候，我们并没有将之前的最小值存起来，我们每次都是通过当前最小值和栈顶元素推出了之前的最小值，所以会省一些空间。
/*
public class MinStack {
    long min;
    Stack<Long> stack;

    public MinStack(){
        stack=new Stack<>();
    }

    public void push(int x) {
        if (stack.isEmpty()) {
            min = x;
            stack.push(x - min);
        } else {
            stack.push(x - min);
            if (x < min){
                min = x; // 更新最小值
            }

        }
    }

    public void pop() {
        if (stack.isEmpty()){
            return;
        }

        long pop = stack.pop();
        //弹出的是负值，要更新 min
        if (pop < 0) {
            min = min - pop;
        }
    }

    public int top() {
        long top = stack.peek();
        //负数的话，出栈的值保存在 min 中
        if (top < 0) {
            return (int) (min);
            //出栈元素加上最小值即可
        } 
        else {
            return (int) (top + min);
        }
    }

    public int getMin() {
        return (int) min;
    }
}
*/



//解法四：不用栈，用链表
//直接用一个链表即可实现栈的基本功能，那么最小值该怎么得到呢？
//我们可以在 Node 节点中增加一个 min 字段，这样的话每次加入一个节点的时候，我们同时只要确定它的 min 值即可。
/*
class MinStack {
    class Node{
        int value;
        int min;
        Node next;

        Node(int x, int min){
            this.value=x;
            this.min=min;
            next = null;
        }
    }
    Node head;
    //每次加入的节点放到头部
    public void push(int x) {
        if(null==head){
            head = new Node(x,x);//头结点是空，那就直接存进去这个数字就行
        }
        else{
            //当前值和之前头结点的最小值较小的做为当前的 min
            Node n = new Node(x, Math.min(x,head.min));
            n.next=head;//新节点指向上一个head
            head=n;//并且将head更新成这个新节点n
        }
    }

    public void pop() {
        if(head!=null){
            head =head.next;
        }
    }

    public int top() {
        if(head!=null){
            return head.value;
        }
        return -1;
    }

    public int getMin() {
        if(null!=head){
            return head.min;
        }
        return -1;
    }
}
*/
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215

5.收获

辅助栈的思路，可以说是提供了好多类似的题目的解法，后面遇到类似的什么最大栈这种问题，都可以用类似的操作去进行
甚至可以不止两个栈，可以多个栈进行操作，这样可以同时给我们的这个提供好几个功能
我们可以看到解法二和解法三，很好的体现了，想要节省空间，通过增加时间的方法（各种逻辑方法）的目的来达到，我们可以看出算法就是实现逻辑+空间的运用这两者可以相互转化，真正厉害的算法，不是转化，而是直接二者全部降低，这就是数学思想推进的魅力所在.
了解了栈的pop，peek，top方法，pop是出栈，peek是查看，push是入栈
对于链表的设计也有了认识，可以设置很多成员变量，至少得有一个指针变量，一个值变量，也可以加新的值变量来存不同的值
学习到了链表的定义创建方式，想使用链表也可以自己在类中中去定义一个链表的类
见识到了同步和不同步的两种处理方式
再一次强化了使用Math类的Min和Max方法的思维
对于时间复杂度和空间复杂度再进一步的认识，很多时候对于他们的考虑可以更进一步

14、比特位计数（Brian Kernighan算法，动态规划）

1.问题描述

给你一个整数 n ，对于 0 <= i <= n 中的每个 i ，计算其二进制表示中 1 的个数，返回一个长度为 n + 1 的数组 ans 作为答案。

2.示例

示例 1：

输入：n = 2
输出：[0,1,1]
解释：
0 --> 0
1 --> 1
2 --> 10
1
2
3
4
5
6

示例 2：

输入：n = 5
输出：[0,1,1,2,1,2]
解释：
0 --> 0
1 --> 1
2 --> 10
3 --> 11
4 --> 100
5 --> 101
1
2
3
4
5
6
7
8
9

3.提示

0 <= n <= 10^5

4.进阶

很容易就能实现时间复杂度为 O(n log n) 的解决方案，你可以在线性时间复杂度 O(n) 内用一趟扫描解决此问题吗？
你能不使用任何内置函数解决此问题吗？（如，C++ 中的 __builtin_popcount ）

5.具体解法（内置函数，Brian Kernighan算法，动态规划：最高有效位，最低有效位，最低设置位）

//方法一：内置函数：Java的Integer.bitCount


//方法二：Brian Kernighan算法
//原理是：对于任意整数x，令x=x&(x−1)，该运算将x的二进制表示的最后一个1变成0。
//因此，对x重复该操作，直到x变成0，则操作次数即为x的「1的比特数」。
/*
class Solution {
    public int[] countBits(int n) {
        int[] bits = new int[n + 1];//创建一个数组用来存储结果
        for (int i = 0; i <= n; i++) {
            bits[i] = countOnes(i);//每到一个数字都进行一个查1个数的操作并赋值给数组
        }
        return bits;
    }

    public int countOnes(int x) {
        int ones = 0;//临时变量存储1的个数
        while (x > 0) {
            x &= (x - 1);//利用这个x=x&(x−1)，该运算将x的二进制表示的最后一个1变成0
            ones++;
        }
        return ones;
    }
}
*/



//方法三：动态规划：最高有效位
//这个方法的思路：是当计算i的「一比特数」时，如果存在0≤j<i，j的「一比特数」已知，且i和j相比，i的二进制表示只多了一个1，则可以快速得到i的「一比特数」。
//令bits[i] 表示i的「一比特数」，则上述关系可以表示成：bits[i]=bits[j]+1。

//对于正整数x，如果可以知道最大的正整数y，使得 y≤x 且y是2的整数次幂，则y的二进制表示中只有最高位是1，其余都是0，
//此时称y为x的「最高有效位」。令z=x−y，显然0≤z<x，则bits[x]=bits[z]+1。

//为了判断一个正整数是不是2的整数次幂，可以利用方法一中提到的按位与运算的性质。
//如果正整数y是2的整数次幂，则y的二进制表示中只有最高位是1，其余都是0，因此 y&(y-1)=0。
//所以正整数是2的整数幂，当且仅当y&(y-1)=0

//显然，0的「一比特数」为0。
//使用highBit 表示当前的最高有效位，遍历从1到n的每个正整数i，进行如下操作。
//如果 i&(i-1)=0，则令highBit=i，更新当前的最高有效位。
//i比i−highBit 的「一比特数」多1，由于是从小到大遍历每个整数，因此遍历到i时，i−highBit的「一比特数」已知，令bits[i]=bits[i−highBit]+1。
//最终得到的数组bits即为答案。

//方法三的数字举例推导
//0～3 是两位，分别是00，01，10，11，
//然后 4 到 7 是三位，分别是100，101，110，111，
//这不就是前面多了个 1 嘛！ 直接相加就可以了。后面的以此类推即可
//这个就可以用来引入我们的动态规划，非常清晰，自己也应该学会这个先分析的思路


/*
class Solution {
    public int[] countBits(int n) {
        int[] bits = new int[n + 1];
        int highBit = 0;
        for (int i = 1; i <= n; i++) {
            if ((i & (i - 1)) == 0) {
                highBit = i;
            }
            bits[i] = bits[i - highBit] + 1;
        }
        return bits;
    }
}
*/
 
 

//方法四：动态规划：最低有效位
//对于正整数x，将其二进制表示右移一位，等价于将其二进制表示的最低位去掉，得到的数是x/2
//如果bits[x/2]的值已知，就可以得到bits[x]
//如果x是偶数：bits[x]=bits[x/2]
//如果x是奇数：bits[x]=bits[x/2]+1
//上面两种情况可以合并为bits[x]=bits[x/2]加上x除2的余数
//[x/2]可以通过 x>>1 得到，x除2的余数可以用 x&1 得到
//遍历从1到n的每个正整数i，计算bits的值。最终得到的数组bits 即为答案。

/*
class Solution {
    public int[] countBits(int n) {
        int[] bits = new int[n + 1];
        for (int i = 1; i <= n; i++) {
            bits[i] = bits[i >> 1] + (i & 1);
        }
        return bits;
    }
}
 */



//方法五：动态规划：最低设置位
//定义正整数 x 的「最低设置位」为x 的二进制表示中的最低的1所在位。例如10的最低设置位是2（1010）
//令y=x&(x-1)，则 y 为将 x 的最低设置位从 1 变成 0 之后的数
//显然0≤y<x，bits[x]=bits[y]+1
//遍历从 1到 n的每个正整数 i，计算 bits 的值。最终得到的数组 bits 即为答案。

/*
class Solution {
    public int[] countBits(int n) {
        int[] bits = new int[n + 1];
        for (int i = 1; i <= n; i++) {
            bits[i] = bits[i & (i - 1)] + 1;
        }
        return bits;
    }
}
 */
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111

6.收获

数组的定义格式：int [] 名字=new int[n]; 也可以int [] 名字={内容，内容……}
感触到这种将内容进行分开两个方法的形式，避免看起来很繁琐（方法一将查1个数的方法内容单独做了一个方法再调用）
学习到了一个新的算法Brian Kernighan 算法，可以利用他统计1的比特位数

对于任意整数x，令x=x&(x−1)，该运算将x的二进制表示的最后一个1变成0。操作到x==0，操作次数就是1的比特位数

正整数是2的整数幂，当且仅当y&(y-1)=0
学到一个新的位运算的应用：[x/2]可以通过 x>>1 得到，x除2的余数可以用 x&1 得到

15、汉明距离（Brian Kernighan 算法，异或）

1.问题描述

两个整数之间的汉明距离指的是这两个数字对应二进制位不同的位置的数目。

给你两个整数 x 和 y，计算并返回它们之间的汉明距离。

2.示例

示例 1：

输入：x = 1, y = 4
输出：2
解释：
1   (0 0 0 1)
4   (0 1 0 0)
       ↑   ↑
上面的箭头指出了对应二进制位不同的位置。
1
2
3
4
5
6
7

示例 2：

输入：x = 3, y = 1
输出：1
1
2

3.提示

0 <= x, y <= 2^31 - 1

4.具体解法（内置函数，移位实现位计数，Brian Kernighan 算法）

//方法一：内置功能
/*
class Solution {
    public int hammingDistance(int x, int y) {
        return Integer.bitCount(x ^ y);
    }
}
*/


//方法二：移位实现位计数
//具体地，记 s =x⊕y，我们可以不断地检查 s 的最低位，如果最低位为 1，那么令计数器加一，
//然后我们令 s 整体右移一位，这样 s 的最低位将被舍去，原本的次低位就变成了新的最低位。
//我们重复这个过程直到 s=0 为止。这样计数器中就累计了 s 的二进制表示中 1 的数量。
/*
class Solution {
    public int hammingDistance(int x, int y) {
        int s = x ^ y, ret = 0;
        while (s != 0) {
            ret += s & 1;//跟1做位与运算，如果s的最后一位是1，那么结果是1，最后一位是0，那么就是0
            s >>= 1;
        }
        return ret;
    }
}
*/



//方法三：Brian Kernighan 算法
//在方法二中，对于 s=10001100的情况，我们需要循环右移 8 次才能得到答案。
//而实际上如果我们可以跳过两个 1 之间的 0，直接对 1 进行计数，那么就只需要循环 3 次即可。

//我们可以使用 Kernighan 算法进行优化，具体地，该算法可以被描述为这样一个结论：
//记 f(x) 表示 x 和 x−1 进行与运算所得的结果，即 f(x)=x&(x−1)
//那么 f(x) 恰为 x 删去其二进制表示中最右侧的 1 的结果。
//基于该算法，当我们计算出 s =x⊕y，只需要不断让s=f(s)，直到 s=0 即可。
//这样每循环一次，s 都会删去其二进制表示中最右侧的 1，最终循环的次数即为 s 的二进制表示中 1 的数量。
/*
class Solution {
    public int hammingDistance(int x, int y) {
        int s = x ^ y, ret = 0;
        while (s != 0) {
            s &= s - 1;
            ret++;//循环次数等于1的个数
        }
        return ret;
    }
}
 */



//这样简洁的链式写法也可以掌握
 class Solution {
    public int hammingDistance(int x, int y) {
        int res = 0;
        for (int i = 0; i < 32; i++) {
            res += (x>>i) & 1 ^ (y>>i) & 1;
//x右移i位,y也右移i位都去跟1做与运算，各自结果再做异或，如果不同说明一个是1，一个是0，也就是不一样，
//i是最多32位的设定，但是这个比32小的数字是不是相对的还是有一点点浪费
        }
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65

5.收获

学会了一个新的位操作的应用：任何一个数s跟1做位与运算，如果s的最后一位是1，那么结果是1，最后一位是0，那么就是0
这道题也可以用暴力的方式，但是完全不建议，因为我认为这种涉及二进制的问题，位运算是最好的处理方式，思考路线也应该向这个解法上去靠近
不过也可以用暴力法复习到一个知识点就是Integer类的toString方法，这个方法可以给参数进而转换成二进制的，当然也可以用toBinaryString方法
链式写法可以开始接触，高手，看起来代码短，但不够清晰
Brian Kernighan 算法在这种位运算的题目中真的是很有用处，要有使用的想法

16、找到所有数组中消失的数（哈希表，Set集合）

1.问题描述

给你一个含 n 个整数的数组 nums ，其中 nums[i] 在区间 [1, n] 内。请你找出所有在 [1, n] 范围内但没有出现在 nums 中的数字，并以数组的形式返回结果。

2.示例

示例 1：

输入：nums = [4,3,2,7,8,2,3,1]
输出：[5,6]
1
2

示例 2：

输入：nums = [1,1]
输出：[2]
1
2

3.提示

n == nums.length
1 <= n <= 10^5
1 <= nums[i] <= n
4.进阶：你能在不使用额外空间且时间复杂度为 O(n) 的情况下解决这个问题吗? 你可以假定返回的数组不算在额外空间内。

4.具体解法（利用Set集合，利用boolean数组，遍历加n作为判断，哈希表）

//方法一：利用Set：不包含重复元素的集合
//首先遍历一遍nums，并把数字都添加到set集合中
//然后再从1到n进行遍历，如果add(nums[i])成功，他会返回一个true的，成功那么给队列也执行一个add


/*
class Solution {
    public List<Integer> findDisappearedNumbers(int[] nums) {
        List<Integer> res = new ArrayList<>();//创建一个集合来存储
        HashSet<Integer> set = new HashSet<>();//创建一个Set集合的实现对象HashSet
        for (int i = 0; i <nums.length; i++) {
            set.add(nums[i]);//如果有了他就添加不进去，也不会报错的
        }
        for (int i = 1; i <= nums.length; i++) {
            if(set.add(i)){
                res.add(i);
            }
        }
        return res;
    }
}
*/


//方法二：我们可以用一个哈希表记录数组 nums 中的数字，由于数字范围均在 [1,n] 中，
//记录数字后我们再利用哈希表检查[1,n] 中的每一个数是否出现，从而找到缺失的数字。
//由于数字范围均在 [1,n] 中，我们也可以用一个长度为 n 的数组来代替哈希表。
//这一做法的空间复杂度是 O(n) 的。我们的目标是优化空间复杂度到 O(1)。
/*
class Solution {
    public List<Integer> findDisappearedNumbers(int[] nums) {
        Map<Integer,Integer> zs=new HashMap<>();
        //题目说以数组形式返回
        //我就写了个int [] res= new int[n];//会报错
        //得用List来做返回，这个点得注意，应该是返回的结果必须的变长的
        List<Integer> res=new ArrayList<>();
        for(int i=0;i<nums.length;i++){
            if(!zs.containsKey(nums[i])){
                //哈希表的装入是put，一开始写成了add
                zs.put(nums[i],nums[i]);
            }
        }
        //这个for循环一开始我写的是k<=n;因为是从1到n遍历嘛，后面才发现，没有n传送过来的，题目说的n是长度，得用length获得
        for(int k=1;k<=nums.length;k++){
            if(!zs.containsKey(k)){
                res.add(k);
            }
        }
        return res;
    }
}
*/




//方法三：
//因为nums的长度恰好为n，nums的数字范围也在[1，n]之间，可以利用这个数字范围之外的数字来表达是否存在。具体怎么操作呢？
//我们首先遍历nums，每遇到一个数x，就让nums[x-1]+n，因为nums数组中的元素范围，所以加n以后，这些数肯定都大于n
//最后我们遍历nums[i]，如果不大于n，就说明没遇到过数i+1，也就找到了缺失的数字
//这个巧妙之处在于，存储的时候就是存到对应的x-1的下标位置处
//而且有的数可能出现两次，就应该对这个数去进行%n处理，下面代码的做法是存储的时候，遍历的时候就拿到一个数先%n，因为都小于n嘛，加过n的自然可以模掉
//我想的是可以在往ret集合存储的时候%n，也就是ret.add((i%n)+1),应该是这两种方式都ok
/*
class Solution {
    public List<Integer> findDisappearedNumbers(int[] nums) {
        int n = nums.length;
        for (int num : nums) {
            int x = (num - 1) % n;//对n取模拿到他原来的值
            nums[x] += n;//注意此处的nums[x]，跟解释处的nums[x-1]是对应的，代码中的num是上面解释中的x
        }
        List<Integer> ret = new ArrayList<Integer>();
        for (int i = 0; i < n; i++) {
            if (nums[i] <= n) {
                ret.add(i + 1);//如果没被遍历过的就把i+1存到集合中等待返回
            }
        }
        return ret;
    }
}
*/



//方法四：boolean数组
//这个跟方法三异曲同工，但是我觉得更好更清晰，因为其实用大于n的方式，本身就是一种true和false的记录，还不如这个清晰呢
/*
class Solution {
    public List<Integer> findDisappearedNumbers(int[] nums) {
        List <Integer> list = new ArrayList<>();
        //定义一个boolean的数组记录1-n出现的数字
        boolean b[] = new boolean[100001];//这里其实可以用MAX_VALUE
        //如果出现就令其值为true
        for(int n : nums){
            b[n] = true;
        }
        //遍历1-n,如果为false 表示未出现。即为所求。
        for(int i=1;i<=nums.length;i++){
            if(!b[i])
                list.add(i);
        }
        return list;
    }
}
 */
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105

6.收获

有一个小疑问或者可以自己记住，问题经常让我们用数组的形式返回一个结果，题目都会用ArrayList来去实现，List不是集合吗

二次回顾感觉应该是返回值得是变长数组的原因。
题目巧妙的利用了Set集合不重复元素的特点，这样的话，我们以后遇到需要有序或者不重复的时候，可以以这道题为提示，想到利用各种特点的集合来去实现我们需要的要求
对于Set集合的add方法也有了新认识，这个方法添加成功之后是会返回一个true的，这个是可以用来做判断的
另外一个思路就是先对数组进行排序，排序之后的数组去进行for循环遍历了。如果i和nums[i]不一样，说明没这个数，这个时候应该移动其中一个指针

怎么去决定移动谁呢我想到用比较的方式，如果i大于nums[i],说明这个数组缺少数字，然后就数组应该往后走，反之应该i继续走，如果相同就是两个人都走。
HashMap的添加方式是put，ArrayList的添加是add
要注意题目中传递给自己的信息有哪些，比如n这个值，是传过来的，还是数组的长度来获取，我们不能直接就去用n
了解到一种类似于标记的方式，我们在遍历的时候可以去存储一些标记信息，加n或者true/false，没有遍历到的自然就没有这个标记，就很容易去找到
List res=new ArrayList<>(); List集合的标准创建代码

17、环形链表（快慢指针，哈希表）

1.问题描述

给你一个链表的头节点 head ，判断链表中是否有环。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。注意：pos 不作为参数进行传递。仅仅是为了标识链表的实际情况。

如果链表中存在环，则返回 true 。否则，返回 false 。

2.示例

示例 1：

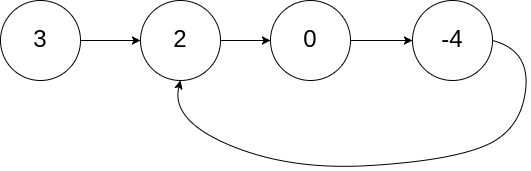
输入：head = [3,2,0,-4], pos = 1
输出：true
解释：链表中有一个环，其尾部连接到第二个节点。
1
2
3

示例 2：

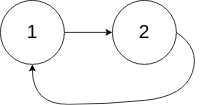
输入：head = [1,2], pos = 0
输出：true
解释：链表中有一个环，其尾部连接到第一个节点。
1
2
3

示例 3：

输入：head = [1], pos = -1
输出：false
解释：链表中没有环。
1
2
3

3.提示

链表中节点的数目范围是 [0, 104]
-10^5 <= Node.val <= 10^5
pos 为 -1 或者链表中的一个有效索引。

4.进阶

你能用 O(1)（即，常量）内存解决此问题吗？

5.具体解法（哈希表，快慢指针，利用数据漏洞）

//方法一：哈希表
//我们可以使用哈希表来存储所有已经访问过的节点。
//每次我们到达一个节点，如果该节点已经存在于哈希表中，则说明该链表是环形链表，否则就将该节点加入哈希表中。
//重复这一过程，直到我们遍历完整个链表即可。
/*
public class Solution {
    public boolean hasCycle(ListNode head) {
        //创建一个HashSet，这样存储的是不重复的元素，方便后面通过add的成功与否去判断是否遍历过这个元素
        Set<ListNode> seen = new HashSet<ListNode>();
        while (head != null) {//只要结点不为空，就继续遍历
            if (!seen.add(head)) {//添加失败说明已经遍历过，是false，然后取反就是true，所以有环下面返回true
                return true;
            }
            head = head.next;
        }
        return false;//如果遍历完成还没退出，说明没有环，那么就返回fasle（无环）
    }
}
*/



//方法二：快慢指针
//我们定义两个指针，一快一满。
//慢指针每次只移动一步，而快指针每次移动两步。
//初始时，慢指针在位置 head，而快指针在位置 head.next。
//这样一来，如果在移动的过程中，快指针反过来追上慢指针，就说明该链表为环形链表。否则快指针将到达链表尾部，该链表不为环形链表。
//为什么我们要规定初始时慢指针在位置 head，快指针在位置 head.next，而不是两个指针都在位置 head（即与「乌龟」和「兔子」中的叙述相同）
//因为如果一开始一样，我们使用的是 while 循环，循环条件先于循环体。
//由于循环条件一定是判断快慢指针是否重合，如果我们将两个指针初始都置于 head，那么 while 循环就不会执行。
//因此我们可以假想一个在head之前的虚拟节点，慢指针从虚拟节点移动一步到达head，快指针从虚拟节点移动两步到达head.next，这样我们就可以使用while循环了。
//当然，我们也可以使用 do-while 循环。此时，我们就可以把快慢指针的初始值都置为 head。

/*
public class Solution {
    public boolean hasCycle(ListNode head) {
        if (head == null || head.next == null) {//两个结点一开始指的结点都是空的，那肯定没环
            return false;
        }
        ListNode slow = head;
        ListNode fast = head.next;//给两个指针赋值初始的位置
        while (slow != fast) {//只要两个指针没指到一起就继续循环
            if (fast == null || fast.next == null) {//两个结点都为走到空了，说明是不存在环的
                return false;
            }
            slow = slow.next;
            fast = fast.next.next;//没空那就往后走
        }
        return true;//只要两个指针指到一起就说明是有环
    }
}
 */


//利用题目数据范围漏洞（不正经解法）
//因为结点数量最大为10000，所以一旦能循环1w次以上那么必定存在环
/*
public boolean hasCycle(ListNode head){
        int n = 0;
        while(head){//这一句会报错，意思是这个意思，使用的话还得再调整
           head = head->next;
           n++;
           if(n > 10000){
               return true;
           }
           return false;
        }
}
*/
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69

6.收获

对HashSet和HashMap的区别有了更清楚的认识，因为二者一个是不能存储重复值的，不能存储相同的元素，所以有些时候需要只存储一遍的可以用Set的特殊性质，并且可以利用add时成功会返回true，失败会返回false来作为一个判断是否有重复元素的条件.
接触到了快慢指针的思想，刚看到很熟悉，想了半天想起来是学数据结构的时候有学习到过，这次很好的复习了这个处理链表中是否有环的思想.
方法一的程序对于新手是很好的，对于链表的移动有了见识，就是用head=head.next这种来进行一个赋值，这样就开始对head的下一个元素进行操作了。而且对于哈希表的建立、add方法的使用又进行了相关的复习和练习.
可以按着 fast.next.next这样去一次移动两个指针，链式编程.
对于链表的遍历有了学习和掌握，就是用head！=null来进行判断配合head=head.next不断进行遍历

18、相交链表（哈希表，双指针）

1.问题描述

给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点，返回 null 。

图示两个链表在节点 c1 开始相交：

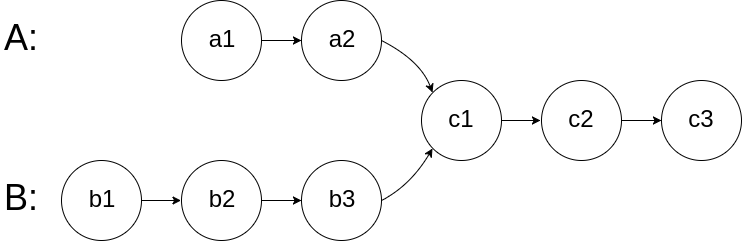
题目数据保证整个链式结构中不存在环。

注意，函数返回结果后，链表必须保持其原始结构。

2.自定义评测

评测系统 的输入如下（你设计的程序不适用此输入）：

intersectVal - 相交的起始节点的值。如果不存在相交节点，这一值为 0
listA - 第一个链表
listB - 第二个链表
skipA - 在 listA 中（从头节点开始）跳到交叉节点的节点数
skipB - 在 listB 中（从头节点开始）跳到交叉节点的节点数
评测系统将根据这些输入创建链式数据结构，并将两个头节点 headA 和 headB 传递给你的程序。如果程序能够正确返回相交节点，那么你的解决方案将被视作正确答案。

3.示例

示例 1：

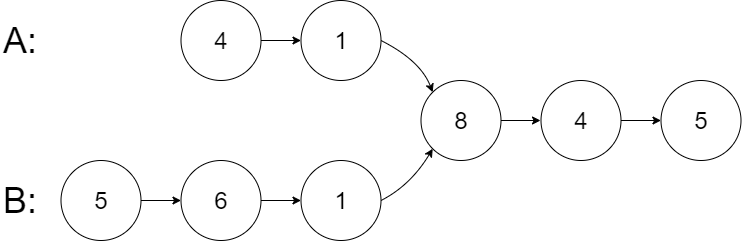
输入：intersectVal = 8, listA = [4,1,8,4,5], listB = [5,6,1,8,4,5], skipA = 2, skipB = 3
输出：Intersected at '8'
解释：相交节点的值为 8 （注意，如果两个链表相交则不能为 0）。
从各自的表头开始算起，链表 A 为 [4,1,8,4,5]，链表 B 为 [5,6,1,8,4,5]。
在 A 中，相交节点前有 2 个节点；在 B 中，相交节点前有 3 个节点。
1
2
3
4
5

示例 2：

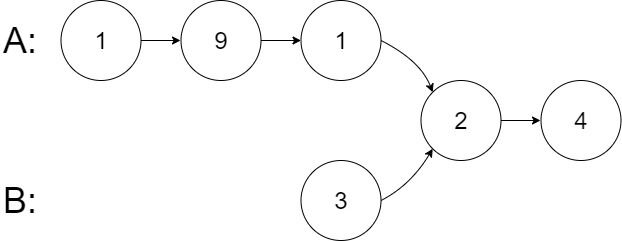
输入：intersectVal = 2, listA = [1,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
输出：Intersected at '2'
解释：相交节点的值为 2 （注意，如果两个链表相交则不能为 0）。
从各自的表头开始算起，链表 A 为 [1,9,1,2,4]，链表 B 为 [3,2,4]。
在 A 中，相交节点前有 3 个节点；在 B 中，相交节点前有 1 个节点。
1
2
3
4
5

示例 3：

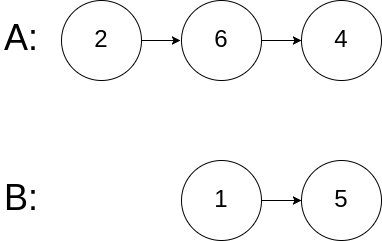
输入：intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
输出：null
解释：从各自的表头开始算起，链表 A 为 [2,6,4]，链表 B 为 [1,5]。
由于这两个链表不相交，所以 intersectVal 必须为 0，而 skipA 和 skipB 可以是任意值。
这两个链表不相交，因此返回 null 。
1
2
3
4
5

4.提示

listA 中节点数目为 m
listB 中节点数目为 n
1 <= m, n <= 3 * 104
1 <= Node.val <= 105
0 <= skipA <= m
0 <= skipB <= n
如果 listA 和 listB 没有交点，intersectVal 为 0
如果 listA 和 listB 有交点，intersectVal == listA[skipA] == listB[skipB]

5.进阶

你能否设计一个时间复杂度 O(m + n) 、仅用 O(1) 内存的解决方案？

6.具体解法（哈希表，双指针）

package day9_相交链表;

//方法一：哈希表
//判断两个链表是否相交，可以使用哈希集合存储链表节点。
//首先遍历链表 headA，并将链表 headA 中的每个节点加入哈希集合中。

//然后遍历链表 headB，对于遍历到的每个节点，判断该节点是否在哈希集合中：
//如果当前节点不在哈希集合中，则继续遍历下一个节点；
//如果当前节点在哈希集合中，则后面的节点都在哈希集合中，即从当前节点开始的所有节点都在两个链表的相交部分，
//因此在链表 headB 中遍历到的第一个在哈希集合中的节点就是两个链表相交的节点，返回该节点。

//如果链表 headB 中的所有节点都不在哈希集合中，则两个链表不相交，返回null。

//关键就是这句话“链表 headB 中遍历到的第一个在哈希集合中的节点就是两个链表相交的节点",理解他就知道这道题想要什么了
/*
public class Solution {
    public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
        Set<ListNode> visited = new HashSet<ListNode>();
        ListNode temp = headA;
        while (temp != null) {
            visited.add(temp);
            temp = temp.next;
        }
        temp = headB;
        while (temp != null) {
            if (visited.contains(temp)) {
                return temp;
            }
            temp = temp.next;
        }
        return null;
    }
}
 */

//方法二：双指针，可以将空间复杂度降至 O(1)

//只有当链表headA和headB都不为空时，两个链表才可能相交。因此首先判断链表 headA 和 headB 是否为空，
//如果其中至少有一个链表为空，则两个链表一定不相交，返回 null。

//当链表headA 和 headB 都不为空时，创建两个指针pA和pB，初始时分别指向两个链表的头节点headA和headB，
//然后将两个指针依次遍历两个链表的每个节点。具体做法如下：

//每步操作需要同时更新指针pA和pB。
//如果指针 pA 不为空，则将指针 pA 移到下一个节点；如果指针pB 不为空，则将指针 pB 移到下一个节点。
//如果指针 pA 为空，则将指针 pA 移到链表 headB 的头节点；如果指针 pB 为空，则将指针 pB 移到链表 headA 的头节点。

//当指针 pA 和 pB 指向同一个节点或者都为空时，返回它们指向的节点或者null。

//具体的证明可以看力扣官方解答里面给的，属于数学的知识，我们只记结论使用
/*
public class Solution {
    public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
        if (headA == null || headB == null) {
            return null;
        }
        ListNode pA = headA, pB = headB;
        while (pA != pB) {
            pA = pA == null ? headB : pA.next;
            pB = pB == null ? headA : pB.next;
        }
        return pA;
    }
}
 */
 

//方法三：使用判断是否有环并返回第一个环节点的思路
//没去细看懂，效率是最好的这个代码
/*
class Solution {
    public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
        if (headA == null || headB == null) {
            return null;
        }
        ListNode last = headB;
        while (last.next != null) {
            last = last.next;
        }
        last.next = headB;

        ListNode fast = headA;
        ListNode slow = headA;

        while (fast != null && fast.next != null) {
            slow = slow.next;
            fast = fast.next.next;
            if (slow == fast) {
                slow = headA;
                while (slow != fast) {
                    slow = slow.next;
                    fast = fast.next;
                }
                last.next = null;
                return fast;
            }
        }
        last.next = null;
        return null;
    }
}
*/
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102

7.收获

这道题如果知道其题目条件和他想要的结果，其实不难，关键是题目一开始没有读懂
这道题跟力扣142题相近，可以互相参考，将其中的一个链表练成环，然后就是 142
为什么示例中相交链表的节点不是从1开始，而是从8开始？相交的节点肯定是内存中的同一个节点，内存地址要相同。不能单单根据节点存的数值判断。
哈希表中是可以存结点这种类型的，应该有这个思想，不要总觉得是存Integer这种

19、反转链表（栈，递归，迭代，双指针，头插法）

1.问题描述

给你单链表的头节点 head ，请你反转链表，并返回反转后的链表。

2.示例

示例 1：

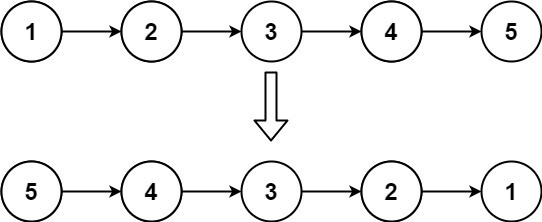
输入：head = [1,2,3,4,5]
输出：[5,4,3,2,1]
1
2

示例 2：

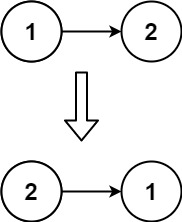
输入：head = [1,2]
输出：[2,1]
1
2

示例 3：

输入：head = []
输出：[]
1
2

3.提示

链表中节点的数目范围是 [0, 5000]
-5000 <= Node.val <= 5000

4.进阶

链表可以选用迭代或递归方式完成反转。你能否用两种方法解决这道题？

5.具体解法（栈，迭代，递归，双指针，头插法）

//方法一：利用栈
//自己第一时间想到的方法，可以遍历链表用栈来做存储，然后重新遍历链表再同时进行赋值
//第一次AC，时间超过百分之百，跨时代的进步
/*
class Solution {
    public ListNode reverseList(ListNode head) {
        ListNode head2 = head;//这个可以理解为一个哨兵，因为我们后面要二次从头遍历链表，头结点在第一次遍历中会丢失，用它做一个存储
        ListNode head3 = head;//这个head3是为了第二次遍历之后，我们需要返回链表，所以得有一个头结点
        Deque<Integer> stk = new LinkedList<>();
        while (head != null) {
            stk.push(head.val);//第一遍遍历，把链表值存进栈
            head = head.next;
        }
        while (head2 != null) {
            head2.val = stk.pop();//第二遍遍历，再把栈的值存回去
            head2 = head2.next;
        }
        return head3;//返回最初的头结点地址即可
    }
}
*/



//方法二：迭代
//假设链表为1→2→3→∅，我们想要把它改成∅←1←2←3。
//在遍历链表时，将当前节点的next 指针改为指向前一个节点。
//由于节点没有引用其前一个节点，因此必须事先存储其前一个节点。在更改引用之前，还需要存储后一个节点。最后返回新的头引用。
//画个图去推导是最清楚的
/*
class Solution {
    public ListNode reverseList(ListNode head) {
        ListNode prev = null;//相当于加了一个空节点在前面帮助处理
        ListNode curr = head;//第一个处理的结点是头结点
        //循环里的这几步就是把curr一左一右两边的结点调换了顺序，然后把curr看做prev，curr.next作为下一个curr继续操作
        while (curr != null) {
            ListNode next = curr.next;
            curr.next = prev;
            prev = curr;
            curr = next;
        }
        return prev;
    }
}
 */

//方法三：递归
//递归版本稍微复杂一些，其关键在于反向工作。假设链表的其余部分已经被反转，现在应该如何反转它前面的部分？
//通过自己列链表推导了一遍，明白了代码各自的含义，下面就来解析下面代码的流程（举例abcde）
//首先系统会调用reverseList方法，此时传来的参数额首结点a，因为a和b，也就是代码中的head和head.next都不为null，所以往下进行
//会创建一个newHead结点并且等于调用head.next，这样会层层传递并且判断head和head.next是不是有为null
//直到最后一次传过去的是最后一个结点（例子中我们举到e），判断e.next=null;所以return head;
//接下来是关键点，形参和实参的注意点了，if中写的是return head，也就是形参，而当时实际传过来的是上一次调用reverseList(head.next);参数是e
//所以返回的是e，也就是ListNode newHead =e;
//注意此时的head是d（这句话非常重要）
//接下来继续执行head.next.next = head;这样就让e的下一个结点变成了d
//然后是head.next = null;这样就让d的下一个结点变成了null
//然后返回newHead，也就是e
//退回到再上一层的reverseList(head.next)调用处，还是ListNode newHead =e;并且此时的head是c了
//以此类推，知道退回到最先一次调用的时候，此时head是a
//所以最后执行完是a指向空，newHead=e，方法返回newHead给最初调用函数的地方
//所以newHead存的是最后反转完的链表的头结点，而尾结点也被设计成了指向null，因为如果不设定可能会出现环
//因为不设定，可能最后就会是2指向1，1指向2
//这个设计太巧妙了，根本想象不到是怎么设计出来的，我们光是理解就要花费很多时间
//不过从中还是学到了一个技巧，就是head.next.next = head;这一句可以让反转的效果出现
//怎么理解呢，就是比如abcde，此时已经反转了一部分，也就是abc还是从前往后指，de是e指向d了，而且c还是指向d的这么一个情况
//那么此时head是c的话，head.next就是dhead.next.next也就是d.next，这个时候让它等于head，就实现了d指向c

/*
class Solution {
    public ListNode reverseList(ListNode head) {
        if (head == null || head.next == null) {
            return head;
        }
        ListNode newHead = reverseList(head.next);//从头结点开始一直会调用，直到最后一个结点，才开始因为上面的if而返回
        head.next.next = head;//进行指向的反向
        head.next = null;//让当前的最后一个结点始终指向null，防止出现环
   //断开原有链表，这六个字是网友给的一个解释，应该是比较专业的说法，其实就是避免出现环，因为我之前指向你，现在你指向我了，我指你的就断开设计为null
        return newHead;//返回newHead，而代码对于newHead的操作很少，其是一直都是最后那个结点
    }
}
*/


//方法四，比较整洁的一个写法
/*
class Solution {
    public ListNode reverseList(ListNode head) {
        ListNode ans = null;
        for (ListNode x = head; x != null; x = x.next) {
            ans = new ListNode(x.val,ans);
        }
        return ans;
    }
}
 */



//方法五：头插法
//使用头插法
//还没理解，有时间再学习掌握把
/*
class Solution {
    public ListNode reverseList(ListNode head) {
        if (head==null || head.next==null) return head;
        ListNode pre = new ListNode();
        ListNode front = head;
        ListNode rear = front.next;
        while (front != null) {
            front.next = pre.next;
            pre.next = front;
            front = rear;
            if (rear != null) {
                rear = rear.next;
            }
        }
        return pre.next;
    }
}
*/



//头插法的另一个写法，做一个补充
/*
public ListNode reverseList(ListNode head) {
      ListNode pre = null;
      ListNode next = null;
      while (head != null) {
         next = head.next;
         head.next = pre;
         pre = head;
         head = next;
      }
      return pre;
   }
 */

//双指针
/*
class Solution {
    public ListNode reverseList(ListNode head) {
        ListNode prev = null;
        ListNode cur = head;
        ListNode temp = null;
        while (cur != null) {
            temp = cur.next;// 保存下一个节点
            cur.next = prev;
            prev = cur;
            cur = temp;
        }
        return prev;
    }
}
 */


//递归的新写法
//用来帮助理解的，有时间可以去看看，理解一下是不是更简洁清晰
/*
class Solution {
    public ListNode reverseList(ListNode head) {
        if(head == null) return head;
        return reverse(null, head);
    }
    private ListNode reverse(ListNode pre, ListNode cur) {
        if(cur == null)return pre;
        // 反转当前cur的指针，本来指向next，改为指向pre
        ListNode next = cur.next;
        cur.next = pre;
        return reverse(cur, next); // 递归
    }
}
*/


//辅助理解递归，看看哪个简洁清晰
/*
class Solution {
    public ListNode reverseList(ListNode head) {
        if (head == null || head.next == null) {
            return head;
        }
        // 想象递归已经层层返回，到了最后一步
        // 以链表 1->2->3->4->5 为例，现在链表变成了 5->4->3->2->null，1->2->null（是一个链表，不是两个链表）
        // 此时 newHead是5，head是1
        ListNode newHead = reverseList(head.next);
        // 最后的操作是把链表 1->2->null 变成 2->1->null
        // head是1，head.next是2，head.next.next = head 就是2指向1，此时链表为 2->1->2
        head.next.next = head;
        // 防止链表循环，1指向null，此时链表为 2->1->null，整个链表为 5->4->3->2->1->null
        head.next = null;
        return newHead;
    }
}
*/
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197

6.收获

自己写出了使用栈解决的形式，还练习了链表的遍历
注意到了栈和哈希表存储链表的区别，哈希表是a.add(head),而栈是a.push(head.val)
第一次AC，时间超过百分之百，跨时代的进步
发现链表遍历结束之后，因为不断next的原因，导致最初的head会消失，所以如果还需要最初的head，那么应该用哨兵结点的思想提前存储好，我甚至是因为遍历两遍，所以存了两个哨兵结点
关于递归，准备了两个代码，可以试着用来理解一下
关于头插法可以抽空了解一下
递归的关键就是理解newHead是什么，其实newHead就是一个超级头结点，或者说虚拟头结点。它被定义为递的终点处的head节点，然后在归的过程传递回来，顺便将链表反转。
虽然头插法和有一个简洁的方法还有两个递归的写法没去理解，但已经掌握了一个栈和一个迭代和一个递归已经够用了，在精不在多，其他的作为参考与扩展吧。

20、回文链表（双指针）

1.问题描述

给你一个单链表的头节点 head ，请你判断该链表是否为回文链表。如果是，返回 true ；否则，返回 false 。

2.示例

示例 1：

输入：head = [1,2,2,1]
输出：true
1
2

示例 2：

输入：head = [1,2]
输出：false
1
2

3.提示

链表中节点数目在范围[1, 10^5] 内
0 <= Node.val <= 9

4.进阶

你能否用 O(n) 时间复杂度和 O(1) 空间复杂度解决此题？

5.具体解法（双指针，快慢指针，递归，哈希法）

//方法一：将值复制到数组中后用双指针法
//第一步，我们需要遍历链表将值复制到数组列表中。（下面的描述是很标准的遍历链表到数组）
//我们用 currentNode 指向当前节点。
//每次迭代向数组添加 currentNode.val，并更新 currentNode = currentNode.next，当 currentNode = null 时停止循环。
//第二步我们在起点放置一个指针，在结尾放置一个指针，每一次迭代判断两个指针指向的元素是否相同，若不同，返回 false；
//相同则将两个指针向内移动，并继续判断，直到两个指针相遇。

//在编码的过程中，注意我们比较的是节点值的大小，而不是节点本身。
//正确的比较方式是：node_1.val == node_2.val，而 node_1 == node_2 是错误的。

/*
class Solution {
    public boolean isPalindrome(ListNode head) {
        List<Integer> vals = new ArrayList<Integer>();

        // 将链表的值复制到数组中
        ListNode currentNode = head;
        while (currentNode != null) {
            vals.add(currentNode.val);
            currentNode = currentNode.next;
        }

        // 使用双指针判断是否回文
        int front = 0;
        int back = vals.size() - 1;
        while (front < back) {
            if (!vals.get(front).equals(vals.get(back))) {//要去get到值再去比较
                return false;
            }
            front++;
            back--;
        }
        return true;
    }
}
*/


//方法二：递归。为了想出使用空间复杂度为 O(1) 的算法，你可能想过使用递归来解决，但是这仍然需要 O(n) 的空间复杂度。
//算法的正确性在于递归处理节点的顺序是相反的（回顾上面打印的算法），而我们在函数外又记录了一个变量，因此从本质上，我们同时在正向和逆向迭代匹配。
//递归为我们提供了一种优雅的方式来双向遍历节点。
/*
function print_values_in_reverse(ListNode head)
    if head is NOT null
        print_values_in_reverse(head.next)
        print head.val
*/
//如果使用递归反向迭代节点，同时使用递归函数外的变量向前迭代，就可以判断链表是否为回文。

//我自己捋顺发现，这个方法就是巧妙的先用递归调用的方式将一个指针变到了最后一个结点，同时一开始记录了头结点，然后开始两端同时开始遍历
//前面往后走靠的是frontPointer = frontPointer.next;后面往前走靠的是迭代的不断返回

/*
class Solution {
    private ListNode frontPointer;

    private boolean recursivelyCheck(ListNode currentNode) {
        if (currentNode != null) {
            //上一个返回是true，反而不会执行这一句，上一个返回是false才会执行他
            if (!recursivelyCheck(currentNode.next)) {
                return false;
            }
            //判断最后一个和第一个结点的值是不是相同
            if (currentNode.val != frontPointer.val) {
                return false;
            }
            frontPointer = frontPointer.next;
        }
        return true;
    }

    public boolean isPalindrome(ListNode head) {
        frontPointer = head;
        return recursivelyCheck(head);
    }
}
 */

//方法三：快慢指针
//我们可以将链表的后半部分反转（修改链表结构），然后将前半部分和后半部分进行比较。
//比较完成后我们应该将链表恢复原样。虽然不需要恢复也能通过测试用例，但是使用该函数的人通常不希望链表结构被更改。

//整个流程可以分为以下五个步骤：
//找到前半部分链表的尾节点。
//反转后半部分链表。
//判断是否回文。
//恢复链表。
//返回结果。

//执行步骤一，我们可以计算链表节点的数量，然后遍历链表找到前半部分的尾节点。
//我们也可以使用快慢指针在一次遍历中找到：慢指针一次走一步，快指针一次走两步，快慢指针同时出发。当快指针移动到链表的末尾时，慢指针恰好到链表的中间。通过慢指针将链表分为两部分。
//若链表有奇数个节点，则中间的节点应该看作是前半部分。

//步骤二可以使用「206. 反转链表」问题中的解决方法来反转链表的后半部分。

//步骤三比较两个部分的值，当后半部分到达末尾则比较完成，可以忽略计数情况中的中间节点。

//步骤四与步骤二使用的函数相同，再反转一次恢复链表本身。
/*
class Solution {
    public boolean isPalindrome(ListNode head) {
        if (head == null) {
            return true;
        }

        // 找到前半部分链表的尾节点并反转后半部分链表
        ListNode firstHalfEnd = endOfFirstHalf(head);
        ListNode secondHalfStart = reverseList(firstHalfEnd.next);

        // 判断是否回文
        ListNode p1 = head;
        ListNode p2 = secondHalfStart;
        boolean result = true;
        while (result && p2 != null) {
            if (p1.val != p2.val) {
                result = false;
            }
            p1 = p1.next;
            p2 = p2.next;
        }

        // 还原链表并返回结果
        firstHalfEnd.next = reverseList(secondHalfStart);
        return result;
    }

    private ListNode reverseList(ListNode head) {
        ListNode prev = null;
        ListNode curr = head;
        while (curr != null) {
            ListNode nextTemp = curr.next;
            curr.next = prev;
            prev = curr;
            curr = nextTemp;
        }
        return prev;
    }

    private ListNode endOfFirstHalf(ListNode head) {
        ListNode fast = head;
        ListNode slow = head;
        while (fast.next != null && fast.next.next != null) {
            fast = fast.next.next;
            slow = slow.next;
        }
        return slow;
    }
}
*/

//方法四：哈希法
//回文数反转之后不变，一个正向计算哈希值，一个反向计算哈希值，比较反转之前和反转之后的哈希值是否相等

//是否可能正向数和反向数刚好哈希碰撞了？
//当然存在这种可能，毕竟是哈希，算法题可以多修正几次哈希函数使其AC即可，
//工程应用可以先使用哈希判断，如果哈希不相等，那么一定不是回文的，
//如果哈希相等，再按照一般方法检验一次即可，哈希可以预判正确性
/*
class Solution {
    public boolean isPalindrome(ListNode head) {
        ListNode t=head;
        int base = 11, mod = 1000000007;
        int left = 0, right = 0, mul = 1;
        while(t!=null){
            left = (int) (((long) left * base + t.val) % mod);
            right = (int) ((right + (long) mul * t.val) % mod);
            mul = (int) ((long) mul * base % mod);
            t=t.next;
        }
        return left==right;
    }
}
*/
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173

6.收获

对于数组列表和数组以及链表的关系要有所明白。数组列表的容量是可以变化的。其实列表就是我们常用的List，这里就对我们之前的一个疑问进行了解答，明明说是用数组存储，怎么定义了个List，因为List就是可变容量的数组的升级版
学习到了一个快慢指针的用法，就是找到序列的中间点：慢指针一次走一步，快指针一次走两步，快慢指针同时出发。当快指针移动到链表的末尾时，慢指针恰好到链表的中间。
我想到的第一个方法是，用双链表首先把我们得到的单链表做一个存储，然后试着双指针从两端进行一个遍历对比，但我还不太会
另外想到的一个方法是，遍历链表，然后用栈来存储这个数值，遇到相同的就出栈，不同就入栈，当运行结束后，看是不是栈为空
但是很快就想到其不可行了，这个思想类似于有效的括号那道题，但是这个比那个要严格
想到一个方法是把整个链表都反转，用新链表保存旧的，然后同时遍历两个链表去比较
哈希法完全没概念，也没理解，有时间理解一下
标准的遍历链表到数组方法要掌握

21、翻转二叉树（BFS，DFS，递归）

1.问题描述

给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

2.示例

示例 1：

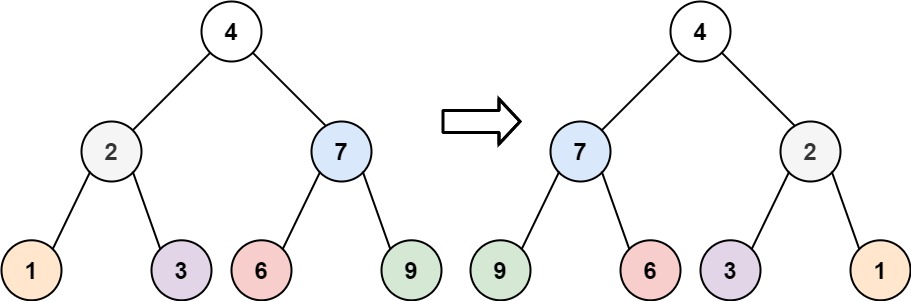
输入：root = [4,2,7,1,3,6,9]
输出：[4,7,2,9,6,3,1]
1
2

示例 2：

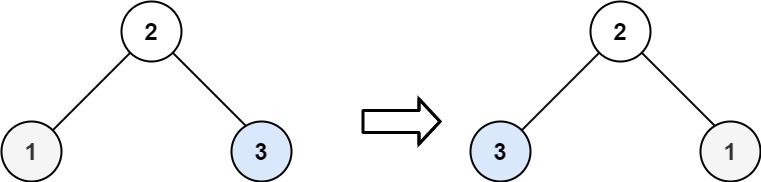
输入：root = [2,1,3]
输出：[2,3,1]
1
2

示例 3：

输入：root = []
输出：[]
1
2

3.提示

树中节点数目范围在 [0, 100] 内
-100 <= Node.val <= 100

4.具体解法（迭代，递归，BFS，DFS，层序遍历）

//第一反应是可以用迭代来作的，只不过没能具体实现
//方法一：递归
//我们从根节点开始，递归地对树进行遍历，并从叶子节点先开始翻转。
//如果当前遍历到的节点 root 的左右两棵子树都已经翻转，那么我们只需要交换两棵子树的位置，即可完成以 root 为根节点的整棵子树的翻转。

//代码的思路可以自己捋顺一下来理解
/*
class Solution {
    public TreeNode invertTree(TreeNode root) {
        if (root == null) {
            return null;
        }
        TreeNode left = invertTree(root.left);
        TreeNode right = invertTree(root.right);
        root.left = right;
        root.right = left;
        return root;
    }
}
*/


//下面的这个递归是从上往下的，更容易理解
/*
public TreeNode invertTree(TreeNode root) {
        
        if (root == null) {
            return null;
        }
        
        //这三步是将根节点的左右结点调换
        TreeNode temp = root.left;
        root.left = root.right;
        root.right = temp;
        
        //然后再去分别调用左右结点的各自的左右结点
        invertTree(root.left);
        invertTree(root.right);
        return root;
}
*/



//一个更简洁的递归代码
//这个递归就是直接把右子树的反转赋给左指向，然后左指向再反转赋给右指向
/*
class Solution {
    public TreeNode invertTree(TreeNode root) {
        if (root == null)
            return root;
        TreeNode temp = root.left;
        root.left = invertTree(root.right);
        root.right = invertTree(temp);
        return root;
    }
}
*/



//方法二：层序遍历
//二次回顾，这个方法跟从上到下的迭代很像，唯一的区别是迭代的过程被我们自己用一个栈给实现了，用栈存储了中间的过程
/*
public TreeNode invertTreeByQueue(TreeNode root) {
        if (root == null) {
            return null;
        }
        Queue<TreeNode> queue = new ArrayDeque<>();
        queue.offer(root);
        while (!queue.isEmpty()) {
            TreeNode node = queue.poll();
            //交换根结点的左右结点
            TreeNode temp = node.left;
            node.left = node.right;
            node.right = temp;
            //然后再去交换子树的
            if (node.left != null) {
                queue.offer(node.left);
            }
            if (node.right != null) {
                queue.offer(node.right);
            }
        }
        return root;
}
*/



//方法三：深度优先遍历
/*
private TreeNode invertTreeByStack(TreeNode root) {
        if (root == null) {
            return null;
        }
        Stack<TreeNode> stack = new Stack<>();
        stack.push(root);
        while (!stack.isEmpty()) {
            int size = stack.size();
            for (int i = 0; i < size; i++) {
                 TreeNode cur = stack.pop();
                 TreeNode temp = cur.left;
                 cur.left = cur.right;
                 cur.right = temp;
                 if (cur.right != null) {
                     stack.push(cur.right);
                 }
                 if (cur.left != null) {
                     stack.push(cur.left);
                 }
            }
        }
        return root;
}
*/
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116

5.收获

发现很多迭代的思路是可以自己看代码明白，但是不能自己想到，理解本身就是一个很难的事情了，不知道他们怎么设计出来的，但有进步的一点是，已经可以一下子就明白迭代会是进行到最后再一步步回来的这样的一个思路了
迭代中经常有调用返回，和当前的一个值的情况，一定要想清楚，一定要找好迭代的出口
自己有感悟，而且也有人提，好多解法其实都对应着前序遍历，中序遍历，后序遍历
对于BDF，DFS还是要去好好的学习掌握一下的
这道题目使用前后遍历都行，中序遍历不好，会翻转两次
对于递归的底层使用栈进行一个实现有了感触，我们的层序遍历用栈存储中间待做的结点，就是一个递归的效果。这个好像也是递归像迭代的转换思路

22、二叉树的直径（BFS）

1.问题描述

给定一棵二叉树，你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点。

2.示例

示例 :
给定二叉树

返回 3, 它的长度是路径 [4,2,1,3] 或者 [5,2,1,3]。

3.注意

两结点之间的路径长度是以它们之间边的数目表示。

4.具体解法（深度优先搜索）

//方法一：深度优先搜索
//首先我们知道一条路径的长度为该路径经过的节点数减一，所以求直径（即求路径长度的最大值）等效于求路径经过节点数的最大值减一。

//而任意一条路径均可以被看作由某个节点为起点，从其左儿子和右儿子向下遍历的路径拼接得到。
//对于该节点的左儿子向下遍历经过最多的节点数 L（即以左儿子为根的子树的深度） 和其右儿子向下遍历经过最多的节点数 R 即以右儿子为根的子树的深度）
//那么以该节点为起点的路径经过节点数的最大值即为L+R+1

//我们记节点 node 为起点的路径经过节点数的最大值为dnode，那么二叉树的直径就是所有节点dnode的最大值减1
//我们定义一个递归函数 depth(node) 计算dnode函数返回该节点为根的子树的深度。
//先递归调用左儿子和右儿子求得它们为根的子树的深度 L和 R ，则该节点为根的子树的深度即为max(L,R)+1
//该节点的dnode为L+R+1
//递归搜索每个节点并设一个全局变量 ans 记录dnode的最大值，最后返回 ans-1 即为树的直径

/*
class Solution {
    int ans;
    public int diameterOfBinaryTree(TreeNode root) {
        ans = 1;
        depth(root);
        return ans - 1;
    }
    public int depth(TreeNode node) {
        if (node == null) {
            return 0;// 访问到空节点了，返回0
        }
        int L = depth(node.left); // 左儿子为根的子树的深度
        int R = depth(node.right); // 右儿子为根的子树的深度
        ans = Math.max(ans, L+R+1); // 计算d_node即L+R+1 并更新ans
        return Math.max(L, R) + 1; // 返回该节点为根的子树的深度
    }
}
*/


//感觉不用+1和-1这些操作，这样写也能通过而且容易理解点
/*
class Solution {
    int maxd=0;
    public int diameterOfBinaryTree(TreeNode root) {
        depth(root);
        return maxd;
    }
    public int depth(TreeNode node){
        if(node==null){
            return 0;
        }
        int Left = depth(node.left);
        int Right = depth(node.right);
        maxd=Math.max(Left+Right,maxd);//将每个节点最大直径(左子树深度+右子树深度)当前最大值比较并取大者
        return Math.max(Left,Right)+1;//返回节点深度
    }
}
*/
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53

5.收获

请问直接左子树的高度加右子树的高度不行吗？如果某个子树非常平衡且庞大，那么最长的路径就存在于这个树中（这个是我的第一个思路，显然是不可以的）
所以说，学习树很关键的一个就是树的遍历
这题和求二叉树最大路径和（lc124）是基本一致的，如果看作所有节点的value为1，那么求最大路径和的值-1就是最大直径
还有687,最长同值路径也跟这道题的思路一样

23、合并二叉树（BFS，DFS）

1.问题描述

给你两棵二叉树： root1 和 root2 。

想象一下，当你将其中一棵覆盖到另一棵之上时，两棵树上的一些节点将会重叠（而另一些不会）。你需要将这两棵树合并成一棵新二叉树。合并的规则是：如果两个节点重叠，那么将这两个节点的值相加作为合并后节点的新值；否则，不为 null 的节点将直接作为新二叉树的节点。

返回合并后的二叉树。

注意: 合并过程必须从两个树的根节点开始。

2.示例

示例 1：

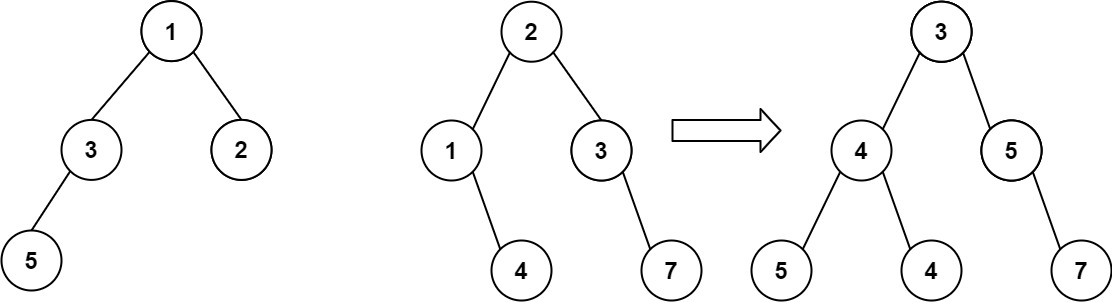
输入：root1 = [1,3,2,5], root2 = [2,1,3,null,4,null,7]
输出：[3,4,5,5,4,null,7]
1
2

示例 2：

输入：root1 = [1], root2 = [1,2]
输出：[2,2]
1
2

3.提示

两棵树中的节点数目在范围 [0, 2000] 内
-10^4 <= Node.val <= 10^4

4.具体解法（深度优先遍历，广度优先遍历）

//可以使用深度优先搜索合并两个二叉树。从根节点开始同时遍历两个二叉树，并将对应的节点进行合并。
//两个二叉树的对应节点可能存在以下三种情况，对于每种情况使用不同的合并方式。

//如果两个二叉树的对应节点都为空，则合并后的二叉树的对应节点也为空；
//如果两个二叉树的对应节点只有一个为空，则合并后的二叉树的对应节点为其中的非空节点；
//如果两个二叉树的对应节点都不为空，则合并后的二叉树的对应节点的值为两个二叉树的对应节点的值之和，此时需要显性合并两个节点。

//对一个节点进行合并之后，还要对该节点的左右子树分别进行合并。这是一个递归的过程。
/*
class Solution {
    public TreeNode mergeTrees(TreeNode t1, TreeNode t2) {
        if (t1 == null) {//t1和t2之中有一个为null的，那应该返回对方
            return t2;
        }
        if (t2 == null) {
            return t1;
        }
        TreeNode merged = new TreeNode(t1.val + t2.val);//用一个新节点来存储链两个树合并的结果
        merged.left = mergeTrees(t1.left, t2.left);
        merged.right = mergeTrees(t1.right, t2.right);//分别对左右子树进行递归的合并
        return merged;
    }
}
*/

//其实也可以不用新建一个结点去存储值的，直接用t1或者t2就可以，因为值不会影响我去判断他的子树
//各自的优缺点也很明显，一个是不改原来的树的结构
/*
class Solution {
    public TreeNode mergeTrees(TreeNode t1, TreeNode t2) {
        if(t1 == null)  return t2;
        if(t2 == null)  return t1;
        t1.val += t2.val;
        t1.left = mergeTrees(t1.left, t2.left);
        t1.right = mergeTrees(t1.right, t2.right);
        return t1;
    }
}
 */

//广度优先搜索
//首先判断两个二叉树是否为空，如果两个二叉树都为空，则合并后的二叉树也为空，如果只有一个二叉树为空，则合并后的二叉树为另一个非空的二叉树。

//如果两个二叉树都不为空，则首先计算合并后的根节点的值，
//然后从合并后的二叉树与两个原始二叉树的根节点开始广度优先搜索，从根节点开始同时遍历每个二叉树，并将对应的节点进行合并。

//使用三个队列分别存储合并后的二叉树的节点以及两个原始二叉树的节点。
//初始时将每个二叉树的根节点分别加入相应的队列。
//每次从每个队列中取出一个节点，判断两个原始二叉树的节点的左右子节点是否为空。
//如果两个原始二叉树的当前节点中至少有一个节点的左子节点不为空，则合并后的二叉树的对应节点的左子节点也不为空。对于右子节点同理。

//如果合并后的二叉树的左子节点不为空，则需要根据两个原始二叉树的左子节点计算合并后的二叉树的左子节点以及整个左子树。考虑以下两种情况：
//如果两个原始二叉树的左子节点都不为空，则合并后的二叉树的左子节点的值为两个原始二叉树的左子节点的值之和，
//在创建合并后的二叉树的左子节点之后，将每个二叉树中的左子节点都加入相应的队列；

//如果两个原始二叉树的左子节点有一个为空，即有一个原始二叉树的左子树为空，
//则合并后的二叉树的左子树即为另一个原始二叉树的左子树，此时也不需要对非空左子树继续遍历，因此不需要将左子节点加入队列。
//
//对于右子节点和右子树，处理方法与左子节点和左子树相同。

/*
class Solution {
    public TreeNode mergeTrees(TreeNode t1, TreeNode t2) {
        if (t1 == null) {
            return t2;
        }
        if (t2 == null) {
            return t1;
        }
        TreeNode merged = new TreeNode(t1.val + t2.val);
        Queue<TreeNode> queue = new LinkedList<TreeNode>();
        Queue<TreeNode> queue1 = new LinkedList<TreeNode>();
        Queue<TreeNode> queue2 = new LinkedList<TreeNode>();
        queue.offer(merged);
        queue1.offer(t1);
        queue2.offer(t2);
        while (!queue1.isEmpty() && !queue2.isEmpty()) {
            TreeNode node = queue.poll(), node1 = queue1.poll(), node2 = queue2.poll();
            TreeNode left1 = node1.left, left2 = node2.left, right1 = node1.right, right2 = node2.right;
            if (left1 != null || left2 != null) {
                if (left1 != null && left2 != null) {
                    TreeNode left = new TreeNode(left1.val + left2.val);
                    node.left = left;
                    queue.offer(left);
                    queue1.offer(left1);
                    queue2.offer(left2);
                } else if (left1 != null) {
                    node.left = left1;
                } else if (left2 != null) {
                    node.left = left2;
                }
            }
            if (right1 != null || right2 != null) {
                if (right1 != null && right2 != null) {
                    TreeNode right = new TreeNode(right1.val + right2.val);
                    node.right = right;
                    queue.offer(right);
                    queue1.offer(right1);
                    queue2.offer(right2);
                } else if (right1 != null) {
                    node.right = right1;
                } else {
                    node.right = right2;
                }
            }
        }
        return merged;
    }
}
 */

//一个更清晰的BFS的解释
//三个队列，分别存root1、root2及俩合并后的节点
//三个队列齐头并进，什么情况下齐头并进呢，
//当root1的left和root2的left都不为空的情况下
//当root1的right和root2的right都不为空的情况下
//其它情况比方说root1为空,root2有值，那自然用root2
//同理，如果root1有值，root2为空，那自然用root1
//如果root1 和root2 都为空，那还有啥好操作的，无需要任何操作

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120

5.收获

对于广度优先遍历的优势还没有感悟，因为这个方法的代码总是比深度优先搜索的代码繁琐很多
官方的dfs可能存在问题，直接return t1，导致的是有一部分内存会和Tree1共享
做这种题目的时候，可以想好到底我的这个要求或者说执行的过程中是不是可以破坏原来的结构和内容，这就涉及了我要不要去新建立一个容器或者设定一个哨兵结点。

2000] 内
-10^4 <= Node.val <= 10^4

4.具体解法（深度优先遍历，广度优先遍历）

//可以使用深度优先搜索合并两个二叉树。从根节点开始同时遍历两个二叉树，并将对应的节点进行合并。
//两个二叉树的对应节点可能存在以下三种情况，对于每种情况使用不同的合并方式。

//如果两个二叉树的对应节点都为空，则合并后的二叉树的对应节点也为空；
//如果两个二叉树的对应节点只有一个为空，则合并后的二叉树的对应节点为其中的非空节点；
//如果两个二叉树的对应节点都不为空，则合并后的二叉树的对应节点的值为两个二叉树的对应节点的值之和，此时需要显性合并两个节点。

//对一个节点进行合并之后，还要对该节点的左右子树分别进行合并。这是一个递归的过程。
/*
class Solution {
    public TreeNode mergeTrees(TreeNode t1, TreeNode t2) {
        if (t1 == null) {//t1和t2之中有一个为null的，那应该返回对方
            return t2;
        }
        if (t2 == null) {
            return t1;
        }
        TreeNode merged = new TreeNode(t1.val + t2.val);//用一个新节点来存储链两个树合并的结果
        merged.left = mergeTrees(t1.left, t2.left);
        merged.right = mergeTrees(t1.right, t2.right);//分别对左右子树进行递归的合并
        return merged;
    }
}
*/

//其实也可以不用新建一个结点去存储值的，直接用t1或者t2就可以，因为值不会影响我去判断他的子树
//各自的优缺点也很明显，一个是不改原来的树的结构
/*
class Solution {
    public TreeNode mergeTrees(TreeNode t1, TreeNode t2) {
        if(t1 == null)  return t2;
        if(t2 == null)  return t1;
        t1.val += t2.val;
        t1.left = mergeTrees(t1.left, t2.left);
        t1.right = mergeTrees(t1.right, t2.right);
        return t1;
    }
}
 */

//广度优先搜索
//首先判断两个二叉树是否为空，如果两个二叉树都为空，则合并后的二叉树也为空，如果只有一个二叉树为空，则合并后的二叉树为另一个非空的二叉树。

//如果两个二叉树都不为空，则首先计算合并后的根节点的值，
//然后从合并后的二叉树与两个原始二叉树的根节点开始广度优先搜索，从根节点开始同时遍历每个二叉树，并将对应的节点进行合并。

//使用三个队列分别存储合并后的二叉树的节点以及两个原始二叉树的节点。
//初始时将每个二叉树的根节点分别加入相应的队列。
//每次从每个队列中取出一个节点，判断两个原始二叉树的节点的左右子节点是否为空。
//如果两个原始二叉树的当前节点中至少有一个节点的左子节点不为空，则合并后的二叉树的对应节点的左子节点也不为空。对于右子节点同理。

//如果合并后的二叉树的左子节点不为空，则需要根据两个原始二叉树的左子节点计算合并后的二叉树的左子节点以及整个左子树。考虑以下两种情况：
//如果两个原始二叉树的左子节点都不为空，则合并后的二叉树的左子节点的值为两个原始二叉树的左子节点的值之和，
//在创建合并后的二叉树的左子节点之后，将每个二叉树中的左子节点都加入相应的队列；

//如果两个原始二叉树的左子节点有一个为空，即有一个原始二叉树的左子树为空，
//则合并后的二叉树的左子树即为另一个原始二叉树的左子树，此时也不需要对非空左子树继续遍历，因此不需要将左子节点加入队列。
//
//对于右子节点和右子树，处理方法与左子节点和左子树相同。

/*
class Solution {
    public TreeNode mergeTrees(TreeNode t1, TreeNode t2) {
        if (t1 == null) {
            return t2;
        }
        if (t2 == null) {
            return t1;
        }
        TreeNode merged = new TreeNode(t1.val + t2.val);
        Queue<TreeNode> queue = new LinkedList<TreeNode>();
        Queue<TreeNode> queue1 = new LinkedList<TreeNode>();
        Queue<TreeNode> queue2 = new LinkedList<TreeNode>();
        queue.offer(merged);
        queue1.offer(t1);
        queue2.offer(t2);
        while (!queue1.isEmpty() && !queue2.isEmpty()) {
            TreeNode node = queue.poll(), node1 = queue1.poll(), node2 = queue2.poll();
            TreeNode left1 = node1.left, left2 = node2.left, right1 = node1.right, right2 = node2.right;
            if (left1 != null || left2 != null) {
                if (left1 != null && left2 != null) {
                    TreeNode left = new TreeNode(left1.val + left2.val);
                    node.left = left;
                    queue.offer(left);
                    queue1.offer(left1);
                    queue2.offer(left2);
                } else if (left1 != null) {
                    node.left = left1;
                } else if (left2 != null) {
                    node.left = left2;
                }
            }
            if (right1 != null || right2 != null) {
                if (right1 != null && right2 != null) {
                    TreeNode right = new TreeNode(right1.val + right2.val);
                    node.right = right;
                    queue.offer(right);
                    queue1.offer(right1);
                    queue2.offer(right2);
                } else if (right1 != null) {
                    node.right = right1;
                } else {
                    node.right = right2;
                }
            }
        }
        return merged;
    }
}
 */

//一个更清晰的BFS的解释
//三个队列，分别存root1、root2及俩合并后的节点
//三个队列齐头并进，什么情况下齐头并进呢，
//当root1的left和root2的left都不为空的情况下
//当root1的right和root2的right都不为空的情况下
//其它情况比方说root1为空,root2有值，那自然用root2
//同理，如果root1有值，root2为空，那自然用root1
//如果root1 和root2 都为空，那还有啥好操作的，无需要任何操作

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120

5.收获

对于广度优先遍历的优势还没有感悟，因为这个方法的代码总是比深度优先搜索的代码繁琐很多
官方的dfs可能存在问题，直接return t1，导致的是有一部分内存会和Tree1共享
做这种题目的时候，可以想好到底我的这个要求或者说执行的过程中是不是可以破坏原来的结构和内容，这就涉及了我要不要去新建立一个容器或者设定一个哨兵结点。

总结

大家坚持看到了这里的话，恭喜大家已经有了一个很不错的收获了，希望和你们一起进步，取得大家心仪的offer，有学习和算法上的问题，来私信我，一起解决。加油！！

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/羊村懒王/article/detail/87314