花生_TL007

这个屌丝很懒，什么也没留下！

热门标签

Leetcode面试经典150题刷题记录——数组 / 字符串篇

作者：花生_TL007 | 2024-04-20 20:51:06

踩

数组 / 字符串篇

==附加题==

有个技巧，若想熟悉语言的写法，可以照着其它语言的题解，写目标语言的代码，比如有C/C++的题解，写Python的算法，这样同时可以对比两种语言，并熟悉Python代码中API的使用，并且可以增强代码的迁移能力，语言只是一种实现的工具，不被语言束缚也是一种自由。

1. 合并两个有序数组

题目链接：合并两个有序数组 - leetcode
题目描述：
给你两个按非递减顺序排列的整数数组 nums1 和 nums2，另有两个整数 m 和 n ，分别表示 nums1 和 nums2 中的元素数目。
请你合并 nums2 到 nums1 中，使合并后的数组同样按非递减顺序排列。
注意：最终，合并后数组不应由函数返回，而是存储在数组 nums1 中。为了应对这种情况，nums1 的初始长度为 m + n，其中前 m 个元素表示应合并的元素，后 n 个元素为 0 ，应忽略。nums2 的长度为 n 。

解题思路：
(1) 排序法。将nums2添加至nums1并排序，但这样的做法未利用到nums1与nums2非递减的特性，时间复杂度是排序的时间复杂度 $O((m+n)log_2(m+n))$ ，空间复杂度认为是快排的空间复杂度 $O(log_2(m+n))$
(2) 双指针法。新建一个数组sorted用来存储，然后将nums1指向新数组的内容，用双指针比较nums1和nums2各元素的大小，存储至sorted数组中

Python3

排序法

class Solution:
    def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:
        """
        Do not return anything, modify nums1 in-place instead.
        """
        nums1[m:] = nums2
        nums1.sort()
1
2
3
4
5
6
7

双指针法

class Solution:
    def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:
        """
        Do not return anything, modify nums1 in-place instead.
        """
        p1, p2 = 0,0
        index_bound1, index_bound2 = m-1,n-1 # 数组下标索引边界，这和长度有区别
        sorted = []
        while p1 <= index_bound1 or p2 <= index_bound2:
            # 1.若有某一数组下标出界，表明该数组已判断完成，应存另一数组的值
            if p1 > index_bound1:
                sorted.append(nums2[p2])
                p2 += 1
            elif p2 > index_bound2:
                sorted.append(nums1[p1])
                p1 += 1
            # 2.比较两数大小，存更小的，以确保是非递减序列
            elif (nums1[p1] <= nums2[p2]):
                sorted.append(nums1[p1])
                p1 += 1
            else:
                sorted.append(nums2[p2])
                p2 += 1
        nums1[:] = sorted
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

2. 移除元素

题目描述：
给你一个数组 nums 和一个值 val，你需要原地移除所有数值等于 val 的元素，并返回移除后数组的新长度。不要使用额外的数组空间，你必须仅使用 O(1) 额外空间并原地修改输入数组。元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
题目归纳：
即要将数值中值等于val的元素全部移除，并且不能使用额外的数组空间

解题思路：
双指针法。left指针从数组起点向右，right指针从数组终点向左，若nums[left]与val相等，就不断的将nums[left]的值与nums[right]的值交换，保证数组在[0,left]的纯洁性。

Python3

class Solution:
    def removeElement(self, nums: List[int], val: int) -> int:
        left, right = 0, len(nums) - 1
        while left <= right:
            if(nums[left] == val): # swap,将等于val的放到数组后面去
                nums[left],nums[right] = nums[right],nums[left]
                right -= 1
            else:
                left += 1
        return left
1
2
3
4
5
6
7
8
9
10

3. 删除有序数组中的重复元素

题目描述：
给你一个非严格递增排列的数组 nums ，请你原地删除重复出现的元素，使每个元素只出现一次，返回删除后数组的新长度。元素的相对顺序应该保持一致。然后返回 nums 中唯一元素的个数。
考虑 nums 的唯一元素的数量为 k ，你需要做以下事情确保你的题解可以被通过：
更改数组 nums ，使 nums 的前 k 个元素包含唯一元素，并按照它们最初在 nums 中出现的顺序排列。nums 的其余元素与 nums 的大小不重要。
返回 k 。
题目归纳：
首先分析该有序数组的特点
由于数组有序，且非严格递增
故对于任意 i < j，若有nums[i] = nums[j]
则有任意i <= k <= j，nums[i] = nums[k] = nums[j]
利用上述特点，使用快慢指针进行删除重复元素

解题思路：
快慢指针法。慢指针用来指向第一个(可能)遇到重复元素的位置处，而快指针寻找新元素，当快指针找到新元素，把新元素赋值给慢指针处做替换。

Python3

class Solution:
    def removeDuplicates(self, nums: List[int]) -> int:
        slow_p = 1 # 数组若只有一个元素，则下标为0, 这样的数组中不会有重复项
        for fast_p in range(1, len(nums), 1):
            if(nums[fast_p-1] != nums[fast_p]): # 快指针找到新元素，利用了任意i <= k <= j，nums[i] = nums[k] = nums[j]特性
                nums[slow_p] = nums[fast_p]
                slow_p += 1 # slow_p的增加是有条件的，要找到不相同的元素
        return slow_p
1
2
3
4
5
6
7
8

6. 轮转数组

题目链接：轮转数组 - leetcode
题目描述：
给定一个整数数组 nums，将数组中的元素向右轮转 k 个位置，其中 k 是非负数。
题目归纳：
题意简单明了。

解题思路：
(1) 解法一： 新建一个数组，将轮转后的元素放至新数组中，再赋值回去。时间复杂度 $O (n)$ ，空间复杂度 $O (n)$ ，空间复杂度 $O (n)$ 还有改进空间。
(2) 解法二： 先掌握空间复杂度 $O (1)$ 下，向右移动一位的操作，再重复 $k$ 遍，也是一样的效果，但是时间复杂度会升至 $O (kn)$ ，很不幸的是，这种方法原理可行，但是leetcode的测试用例会让它超时。
(3) 解法三： 仔细想想，解法二只是理论可行，所以还是要另寻他路，既可以让数组元素移位，又不用开辟新的空间，那路径其实就很明确了，只剩下swap()交换数组元素一条路。观察测试用例：
输入: nums = [1,2,3,4,5,6,7], k = 3
输出: [5,6,7,1,2,3,4]
1
2
其实我们可以通过以下步骤达到目的。
(1)原数组 [1,2,3,4,5,6,7]
(2)反转数组 [7,6,5,4,3,2,1]
[7,  6,  5] ,  [4, 3, 2, 1]
[0 ... k-1] ,  [k   ...  n]
(3)翻转。这就是我们要的结果
[5,  6,  7] ,  [1, 2, 3, 4]
[0 ... k-1] ,  [k   ...  n]
1
2
3
4
5
6
7

Python3

解法一(新数组)

class Solution:
    def rotate(self, nums: List[int], k: int) -> None:
        """
        Do not return anything, modify nums in-place instead.
        """
        # 第一种方法，新建一个数组，先将轮转后的元素放至新数组中，再赋值回去
        # 时间复杂度O(n)
        # 空间复杂度O(n)
        n = len(nums)
        # rotate_nums = copy.deepcopy(nums) # 深拷贝，所有操作不会影响nums。https://zhuanlan.zhihu.com/p/631965597

        rotate_nums = [0 for i in range(0,n)]
        for i in range(0, n):
            rotate_nums[(i+k)%n] = nums[i]
        for i in range(0, n):
            nums[i]= rotate_nums[i] 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

解法二(通过大部分测试用例，但仍旧存在超时)

class Solution:
    def rotate2right_one_step(self, nums: List[int]):
        n = len(nums)
        end = nums[n-1]
        for i in range(n-1, 0, -1):
            nums[i] = nums[i-1]
        nums[0] = end
        return nums

    
    def rotate(self, nums: List[int], k: int) -> None:
        """
        Do not return anything, modify nums in-place instead.
        """
        for i in range(0, k):
            nums = self.rotate2right_one_step(nums)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

解法三(原地翻转法)

class Solution:
    def reverse(self, nums, start, end): # 翻转nums[begin, end]的数组元素
        while start < end:
            nums[start], nums[end] = nums[end], nums[start]
            start += 1
            end -= 1

    def rotate(self, nums: List[int], k: int) -> None:
        """
        Do not return anything, modify nums in-place instead.
        """
        n = len(nums)
        k %= n  # 不要重复向右转圈
            
        self.reverse(nums, 0, n-1)
        self.reverse(nums, 0, k-1)
        self.reverse(nums, k, n-1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

7. 买卖股票的最佳时机

题目链接：买卖股票的最佳时机 - leetcode
题目描述：
给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。你只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。
题目归纳：
先买后卖是常规操作，即做多。而先将股票卖出，后买入同样数量股票归还于他人，即做空，这道题目不考虑做空，考虑做空也简单，把股票价格数组反转一下，还是先买后卖，就变成“做空”了。这道题目等价于：给定数组，求数组中的两个数字间的最大差值。在实际中，相当于你只能买和卖各一次，减法只有一次，解这道题目，代入感不要太强，不要真的以为自己在买股票，然后傻乎乎的去一个个的从左到右遍历，并且假设自己不知道明天的股票价格，你是开了上帝之眼，知道整个股票价格数组的！用爬山类比：相当于只记录从山脚到山顶的高程差。

解题思路：
(1) 记录当前遇到的 min_price 即最低股价
(2) 记录当前收益 = (当前股价 - 最低股价) ，与最大收益做比较并更新最大收益
(3) 返回最大收益

Python3

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        inf = int(1e9) # 10^9
        min_price = inf
        max_profit = 0 # 第一天收益为0
        for price in prices:
            max_profit = max(price - min_price, max_profit) # 这样可以求得全局的最大收益
            min_price = min(price, min_price)
        return max_profit
1
2
3
4
5
6
7
8
9

8. 买卖股票的最佳时机Ⅱ

题目链接：买卖股票的最佳时机Ⅱ - leetcode
题目描述：
给你一个整数数组 prices ，其中 prices[i] 表示某支股票第 i 天的价格。在每一天，你可以决定是否购买和/或出售股票。你在任何时候最多只能持有一股股票。你也可以先购买，然后在同一天出售。返回你能获得的最大利润。
题目归纳：
与上一题的区别：同一天也可以买和卖，并且可以在多天多次买卖，其它条件与前面那道题一致，只能有一只股票。也等价于：给定数组，可以多次求差值(只能后减前)，求数组中的最大 差值总和。用爬山类比：相当于记录从山脚到山顶的高程差之和，即所有上坡高度之和。

解题思路：
(1) 若明天股价大于今天股价，可以卖出。
(2) 只要有股价上涨，就可以卖出。

Python3

贪心法

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        # 贪心解法
        sum_profit = 0
        n = len(prices)
        print(prices[-1]) # 注意python中这样写是没有数组越界的警告的，而是数组的第size-1个元素
        for i in range(1, n): # (1,n)而不是(0,n)
            sum_profit += max(0, prices[i] - prices[i-1]) # 只要有股价上涨，就可以卖出。
        return sum_profit
1
2
3
4
5
6
7
8
9

动态规划法

这题的动态规划算法必须学会，这是解下一步的股票题的基础。

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        # 动态规划解法
        # 考虑一个数组dp
        # dp[i][0] 为，当天未持有股票，所获得的最大收益
        # dp[i][1] 为，当天  持有股票，所获得的最大收益
        # 那么可以列出转移方程：
        # dp[i][0] = max( dp[i-1][0], dp[i-1][1] + prices[i] ) # 之所以加上prices[i]，是因为今天要卖出这只股票，会获得prices[i]这么多的收益
        # 同理
        # dp[i][1] = max( dp[i-1][1], dp[i-1][0] - prices[i]) # 之所以减去prices[i]，是因为今天要买入这只股票，会损失prices[i]这么多的收益

        # 建立dp数组
        n = len(prices)
        rows = n
        cols = 2
        dp = [ [0 for _ in range(cols)]for _ in range(rows) ]

        # 赋初值
        dp[0][0] = 0
        dp[0][1] = -prices[0]
        for i in range(1, n):
            dp[i][0] = max( dp[i-1][0], dp[i-1][1] + prices[i] )
            dp[i][1] = max( dp[i-1][1], dp[i-1][0] - prices[i] )
        
        # 最后一天不能拥有股票，因为还有股票的话肯定是利益受损的
        return dp[n-1][0]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

9. 跳跃游戏

题目链接：跳跃游戏 - leetcode
题目描述：
给你一个非负整数数组 nums ，你最初位于数组的第一个下标。数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个下标，如果可以，返回 true ；否则，返回 false 。
题目归纳：
我想说的是，不要将这道题，仅仅看做一道题目，把它推广到你的人生中去，你会做何选择？这里的数组就像一个个与你有联系的人，不同的人能力、关系范围不同，比如你想获得更好的发展事业，找到更合你心意的伴侣，用这道题的解题方法就是借力打力，骑驴找马，不过这道题与现实的区别在于：现实是会动态变化的，人生也不是只有一个终点。

解题思路：
核心思想就是：永远跳到一个能让你下一步跳到最远的位置。
动态规划法。
贪心法。

Python3

动态规划

class Solution:
    def canJump(self, nums: List[int]) -> bool:
        # 作者：Noah-Blake
        # 链接：https://leetcode.cn/problems/jump-game/
        # 来源：力扣（LeetCode）
        # 著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
        
        # 1.列状态
        # dp[i]: 从[0,i]任意一点出发，最大可以跳到的位置

        # 2.列状态转移方程
        # dp[i] = max(dp[i-1], i+nums[i])，不从下标i出发最大能到达的位置是dp[i-1]，从下标i出发最大能到达的位置是i+nums[i]

        # 3.列边界条件
        # dp[0] = nums[0]

        # 思考，若nums[i] = 0, 且dp[i-1] <= i时, 则dp[i] = i, 即不能再前进了
        n = len(nums)
        if (n == 1): return True
        if (nums[0] == 0): return False

        dp = [0 for _ in range(0, n)]
        # 边界条件
        dp[0] = nums[0]

        for i in range(1, n):
            dp[i] = max(dp[i-1], i+nums[i])
            if(dp[i] >= n - 1): # 可以走到终点
                return True
            if(dp[i] == i): # 不能再前进
                return False
        return True
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

贪心法

10. 跳跃游戏Ⅱ

题目链接：跳跃游戏Ⅱ - leetcode
题目描述：
给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说，如果你在 nums[i] 处，你可以跳转到任意 nums[i + j] 处:
0 <= j <= nums[i]
i + j < n
返回到达 nums[n - 1] 的最小跳跃次数。生成的测试用例可以到达 nums[n - 1]。
题目归纳：
前一题判断能否跳到，这道题是肯定能够跳到，只是求跳跃次数。

解题思路：
(1) 动态规划法。但用时较多。
(2) 贪心法。每次找到可到达的最远位置，就可以在线性时间内得到最少的跳跃次数。
宫水三叶-路径问题

Python3

动态规划法

时间复杂度 = O(n^2): $\sum \limits_{i = 1}^{n-1} {\sum \limits_{j = 0}^{i}} 1 = \frac{n^2 + n - 2}{2}$
空间复杂度 = O(n): 开辟了长度为n的dp数组


class Solution:
    def jump(self, nums: List[int]) -> int:
        # 一、动态规划法
        # 1.定义状态
        # dp[i] 之前所有元素跳跃至第i个元素，最小的跳跃数，这里会多次比较之前的元素，取最小值

        # 2.状态转移方程
        # 假设0<=j<i && j+nums[j]>i,那么可以从j跳到i，跳跃次数为dp[j]+1
        # dp[i] = min(dp[i], dp[j]+1 if j+nums[j] > i) 

        # 3.初始化状态边界
        # dp[i] = n, 每个都初始化为数组长度，答案最多也就是从起点跳到终点，共n-1次
        # dp[0] = 0, dp[0]除外，起点在这里，不用跳

        n = len(nums)
        dp = [n for i in range(0, n)]
        dp[0] = 0

        for i in range(1, n):
            for j in range(0, i):
                if(j+nums[j] >= i):
                    dp[i] = min( dp[i], dp[j]+1 )# 用for j in range(0, i)循环多次比较，取最小值
                    
        return dp[n-1]

# 以上代码与注释参考自:
# 作者：Flokken
# 链接：https://leetcode.cn/problems/jump-game-ii/
# 来源：力扣（LeetCode）
# 著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

贪心法

时间复杂度 = O(n)
空间复杂度 = O(1)

class Solution:
    def jump(self, nums: List[int]) -> int:
        # 方法二：贪心法
        n = len(nums)
        end = 0
        max_position = 0
        steps = 0
        for i in range(0, n-1): # 不访问最后一个元素，在访问最后一个元素前，当前能够到达的最大下标位置一定 >= 最后一个位置，否则无法跳到最后一个位置，若访问最后一个元素，次数会+1
            max_position = max(max_position, i + nums[i])
            if i == end: 
                end = max_position # 下一跳能跳到的最远地方
                steps += 1
        return steps
1
2
3
4
5
6
7
8
9
10
11
12
13

11. H 指数

题目描述：
给你一个整数数组 citations ，其中 citations[i] 表示研究者的第 i 篇论文被引用的次数。计算并返回该研究者的 h 指数。
根据维基百科上 h 指数的定义：h 代表“高引用次数” ，一名科研人员的 h 指数是指，他（她）至少发表了 h 篇论文，并且每篇论文至少被引用了 h 次。如果该 h 有多种可能的值，h 指数是最大的那个。
题目归纳：
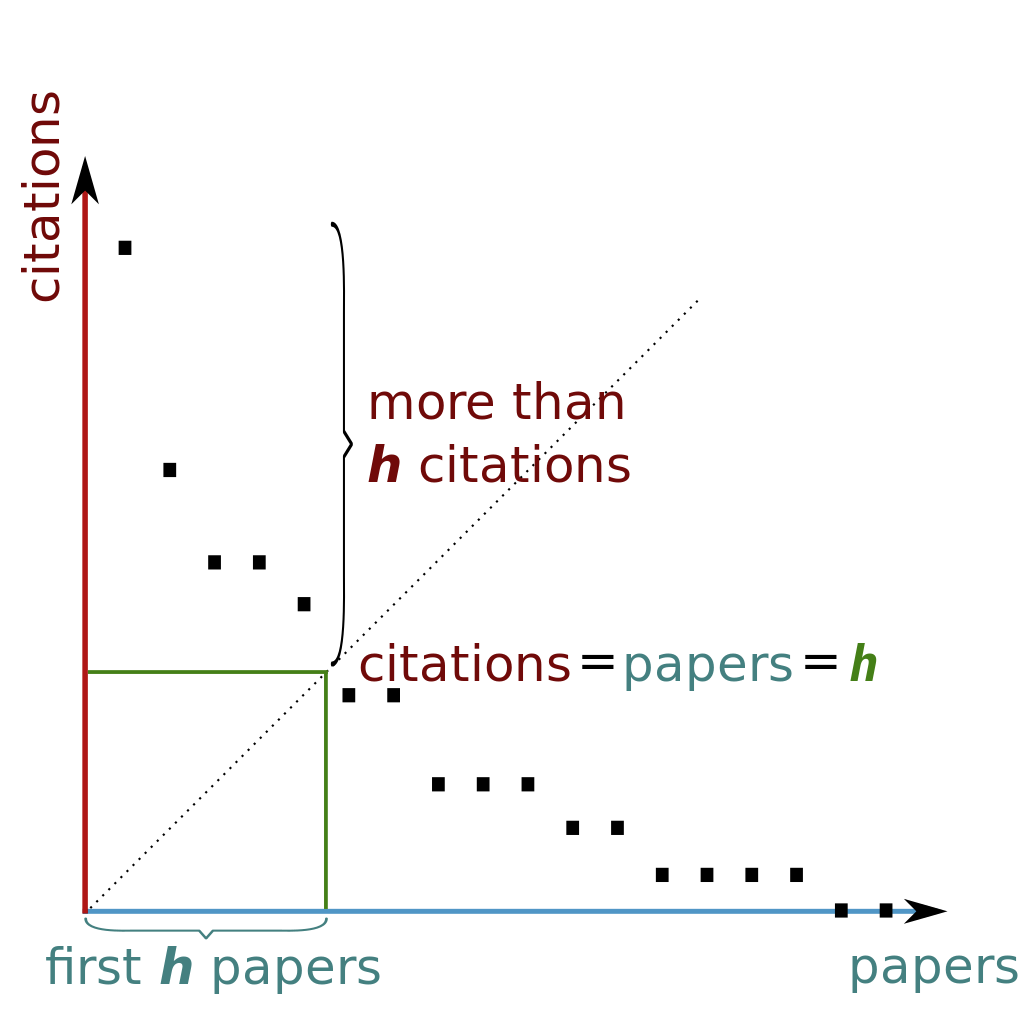
H-index Wiki，我想，h 指数的基本思想是：论文发的越多，不一定代表水平越高，而是发的越多，也要引用的越多才行，引用数认为是质，发表数认为是量，即有质有量 h 指数才高，可以看出原始的 h 指数有个缺点，如果论文发的少引用的多，h 指数也不会很高，也就是有质无量的 h 指数低，无质无量，无质有量自然就更低了，这里把两个量的量纲统一了，就得到了下面的图。

解题思路：
(1) 排序法。将数组citations从高到底排列，h不断增加，直到引用数 h 无法增大，则返回 h 。对应上图，就是寻找到虚线和数据分布的“分界点”，在papers(citations)坐标轴上的值。
(2) 计数排序法。

Python3

排序法

时间复杂度： $O(nlog_{2}{n})$ ， $n$ 为数组citations长度
空间复杂度： $O(log_{2}{n})$ ， $n$ 为数组citations长度

class Solution:
    def hIndex(self, citations: List[int]) -> int:
        sorted_citation = sorted(citations, reverse = True)
        # python里可以用分号在一行中分割语句，曾经python为了阅读的简便性，抛弃了分号，现在又拿回来了，会不会有一天，这些语言来一个大一统，赋值号居然还有:=，=这两种写法，想出:=的人我很好奇他个人的精神状态
        h = 0; i = 0; n = len(citations)
        while i < n and sorted_citation[i] > h:
            h += 1
            i += 1
        return h
1
2
3
4
5
6
7
8
9

计数排序法

【排序算法】计数排序 - bilibili
计数排序是一种非比较排序，比较排序的复杂度下限是O(nlogn)已经得到过论文证明。

class Solution:
    def hIndex(self, citations: List[int]) -> int:
        # 新建并维护一个数组citation_papers，来记录当前引用次数的论文有多少篇
        # 对于论文i引用次数citations[i]超过论文发表数len(citations)的情况，将其按总论文发表数len(citations)计算即可，这样排序的数的大小范围就可以降低至[0,n=len(citations)]
        # 从而计数排序的时间复杂度，就降低至O(n)。现实中，一个学者一辈子能发表的论文数量顶天了也就百来篇，再夸张点，一千篇，不需要考虑n是无穷增长的，这点大小对计数排序是恰到好处的，因为计数排序就适合范围不大的排序。
        n = len(citations); H_papers = 0 # H_papers: 符合H指数的论文数
        citation_papers = [0] * (n+1) # 生成计数排序数组，用到了python的扩充操作，此数组下标为citation，数组内容为paper数量
        
        # 计算计数排序数组
        for c in citations:
            if c >= n:             # 引用次数超过论文发表数，引用次数按发表论文数计算
                citation_papers[n] += 1
            else:
                citation_papers[c] += 1

        # 倒序遍历
        for citation in range(n, -1, -1): # (-1, n] step = -1，实际上的下标范围即[0,n]
            H_papers += citation_papers[citation]
            if citation <= H_papers:
                return citation

        return 0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

二分查找

//@TODO

13. 除自身以外数组的乘积

题目链接：除自身以外数组的乘积 - leetcode
题目描述：
给你一个整数数组 nums，返回数组 answer ，其中 answer[i]等于 nums 中除 nums[i] 之外其余各元素的乘积。题目数据保证数组 nums 之中任意元素的全部前缀元素和后缀的乘积都在 32 位整数范围内。请 不要使用除法，且在 O(n) 时间复杂度内完成此题。
题目归纳：
即左边的所有元素 $\times$ 右边的所有元素，之所以要求不要使用除法，我想是为了避免有元素为0导致算法失败。

解题思路：
(1) 左右乘积列表。
(2) 左右乘积列表的改进。

Python3

左右乘积列表

class Solution:
    def productExceptSelf(self, nums: List[int]) -> List[int]:
        n = len(nums)

        # 列表[]。长度为n，元素为0
        L = list([0] * n)  # 左侧的乘积,列表
        R = list([0] * n)  # 右侧的乘积,列表
        result = list([0] * n)  # 结果,列表

        L[0] = 1
        for i in range(1, n):
            L[i] = L[i-1] * nums[i-1]

        R[n-1] = 1
        for i in range(n-2, -1, -1):
            R[i] = nums[i+1] * R[i+1]

        # Finding result
        for i in range(0, n):
            result[i] = L[i] * R[i]
        
        return result
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

左右乘积列表(改进空间复杂度至 $O (1)$ )

去掉列表L,R，全部过程使用result与变量R迭代。之所以说改进空间复杂度至 $O (1)$ ，返回数组是必须要开辟的，这不可避免，所以返回数组不考虑在空间复杂度中。
这里有一个技巧，这里的将R，从赋值为 列表[] 到赋值为变量，其实是状态压缩的写法，如果遇到了用一次就不再访问，但对后续过程仍有影响的变量值，那么就要考虑可否进行状态压缩。

class Solution:
    def productExceptSelf(self, nums: List[int]) -> List[int]:
        n = len(nums)

        result = list([0] * n)
        
        # 此时result相当于列表L
        result[0] = 1
        for i in range(1, n):
            result[i] = result[i-1] * nums[i-1]

        R = 1 # 不使用列表，而用变量进行迭代并存储结果
        for i in range(n-1, -1, -1):
            result[i] = result[i] * R
            R *= nums[i]

        return result
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

14. 加油站

题目链接：加油站 - leetcode
题目描述：
在一条环路上有 n 个加油站，其中第 i 个加油站有汽油 gas[i] 升。你有一辆油箱容量无限的的汽车，从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发，开始时油箱为空。给定两个整数数组 gas 和 cost ，如果你可以按顺序绕环路行驶一周，则返回出发时加油站的编号，否则返回 -1 。如果存在解，则保证它是唯一的。
题目归纳：

解题思路：
双层循环遍历。当从起点start出发，若无法走完全部n个加油站，那么下一个起点应该是当前正好无法到达的那个加油站。

Python3

class Solution:
    def canCompleteCircuit(self, gas: List[int], cost: List[int]) -> int:
        # 这道题是跳跃数组的一个进化，依旧可以使用DP方法
        # 1. gas[0], gas[1], ... , gas[n-1]
        # 2. cost[0], cost[1], ... , cost[n-1]
        # 若可以按顺序绕环路行驶一周，则返回出发时加油站的编号，否则返回-1。题目保证只有一个唯一解
        
        n = len(gas)
        start = 0  # 初始出发点为0
        while start < n: # 不断迭代更新出发点
            sumOfGas, sumOfCost = 0,0
            cnt = 0  
            while cnt < n: # cnt == n, 则走了完整的一圈
                j = (start + cnt) % n # 注意要对n求余
                sumOfGas += gas[j]
                sumOfCost += cost[j]
                if(sumOfCost > sumOfGas): # 消耗量大于加油量, 以当前i为起点无法走完一圈, 跳出子循环
                    break
                cnt += 1 # 可以走到下一个加油站, cnt+=1，注意这里cnt +=1要放在这个break后面执行
            if(cnt == n): # 走完了整整n个加油站，当前的i即是符合条件的起点
                return start
            else:        # 当从起点start出发，无法走完全部n个加油站，那么下一个起点应该是当前正好无法到达的那个加油站。
                start = start+cnt + 1

        return -1 # 没有符合的条件，return -1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

15. 分发糖果

题目链接：分发糖果 - leetcode
题目描述：
n 个孩子站成一排。给你一个整数数组 ratings 表示每个孩子的评分。你需要按照以下要求，给这些孩子分发糖果：
(1) 每个孩子至少分配到 1 个糖果。
(2) 相邻的两个孩子，评分更高的孩子会获得更多的糖果。
请你给每个孩子分发糖果，计算并返回需要准备的最少糖果数目。
题目归纳：
若将该题推广至社会范围，那解题人，也就是发糖果的人，会变成谁呢？是不是“老板”？由于工资保密制度的存在，对于“ 鹤立鸡群 ”的人，他们只能与周围可以共享信息的人群做比较，并希望得到更高的回报，折算成经济回报即薪资，但由于信息传播的局限性，一个人不可能知道全局的评分，只能观察周围的人，这道题的难度虽然被列为 hard ，但想来平常经过社会的洗涤，这道题的解题思路是必须掌握的。在解完这道题后，让我们计算下，基尼系数是多少。常言道，人类的智商呈正态分布，那么正态分布的Gini系数又是多少？或者说，完全根据能力大小回报劳动价值，而所呈现的正态分布收入，Gini系数会是合理区间吗？

参考文章
《什么是基尼系数》—— 国家统计局
《吉尼系数的计算及正态分布的吉尼系数》

参考文章
《什么是基尼系数》—— 国家统计局
《吉尼系数的计算及正态分布的吉尼系数》

解题思路：
(1) 左右数组，两次遍历。取左右数组中最大的值。
(2) 利用序列连续增长或下降的特性。只要最终结果，而非过程值。

Python3

class Solution:
    def candy(self, ratings: List[int]) -> int:
        # 方法一、两次遍历。有点像左右乘积列表
        # left_rules
        # right_rules

        n = len(ratings)

        # 左规则数组与求解
        left = list([0] * n)
        left[0] = 1 # 左边没人，故对左边进行比较时只要值为1即符合条件
        for i in range(1, n):
            if(ratings[i-1] < ratings[i]): # 大于左边
                left[i] = left[i-1] + 1
            else:
                left[i] = 1
        
        # 右规则与求解，右规则不赋值为数组，直接和左规则数组里的值进行比较即可
        right_val,ret = 0,0 
        gini_arr = []
        for i in range(n-1, -1, -1): 
            if (i < n-1 and ratings[i] > ratings[i+1]): # right_val 在n-1位置为0，右边没人，会跳转到else处
                right_val += 1
            else: 
                right_val = 1
            candy_numsOf_this_child = max(left[i], right_val)
            gini_arr.append(candy_numsOf_this_child)
            ret += candy_numsOf_this_child
        
        print('Gini index = ', self.gini_coefficient(gini_arr))
        return ret

    def gini_coefficient(self, x): # 计算基尼系数
	    n = len(x)
	    x_sorted = sorted(x)
	    numerator = sum([(i+1) * x_sorted[i] for i in range(n)])
	    denominator = n * sum(x_sorted)
	    gini = (2 * numerator) / denominator - (n + 1) / n
	    return gini
        

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

16. 罗马数字转整数

题目链接：罗马数字转整数 - leetcode
题目描述：
给定一个罗马数字，将其转换成整数。
例如：
输入: s = “III”
输出: 3
输入: s = “IV”
输出: 4
题目归纳：
遍历罗马数字字符串，将对应阿拉伯数值相加，若数值小于右边罗马字符数值，则相减。

Python3

class Solution:
    def romanToInt(self, s: str) -> int:
        roman_numerals_dict = { # 罗马数字字典
            'I':1,
            'V':5,
            'X':10,
            'L':50,
            'C':100,
            'D':500,
            'M':1000
        }

        # 将字符串s中的值加起来，若遇到左边小于右边，则要减去，如IV，I<V
        ans = 0
        n = len(s)
        for i in range(0, n):
            ch = s[i]
            value = roman_numerals_dict[ch]
            if(i < n-1 and value < roman_numerals_dict[s[i+1]]): # 小于右边的值则需要减去, if 不是可以随意拆分的，这样会影响下一个else，这里就不能为了阅读的便利而拆分
                ans -= value
            else:
                ans += value
        return ans
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

17. 整数转罗马数字

题目链接：整数转罗马数字 - leetcode
题目描述：
给定一个整数，将其转换成罗马数字。
题目归纳：
与上面这道题题意相反，那么过程呢？

解题步骤：
(1) 建立数值-罗马数字字典。
(2) 从字典中最大数值开始循环，不断减去字典中的数值，并添加到罗马数字字符串roman_str的尾部。

Python3

class Solution:
    # 全局常量，放在类变量区并大写
    NUMERALS_ROMAN_DICT = [ # 数值-罗马数字字典
        (1000, "M"),
        (900, "CM"),
        (500, "D"),
        (400, "CD"),
        (100, "C"),
        (90, "XC"),
        (50, "L"),
        (40, "XL"),
        (10, "X"),
        (9, "IX"),
        (5, "V"),
        (4, "IV"),
        (1, "I")
    ]

    def intToRoman(self, num: int) -> str:
        # 类似于质因数分解，但质因数分解是针对乘法，这里是针对加法，分解成唯一的罗马数字表示

        # 分解规则
        # (1)可能有多个分解方案
        # (2)分解方案应遵循：从左到右的每一位的罗马数字，选择尽可能大的符号值。
        
        roman_str = ""
        for numeral, roman in Solution.NUMERALS_ROMAN_DICT:
            while num >= numeral:
                num -= numeral
                roman_str += roman # 字符串拼接
            if num == 0: # 完成
                break
        return roman_str
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

18. 最后一个单词的长度

题目链接：最后一个单词的长度 - leetcode
题目描述：
给你一个字符串 s，由若干单词组成，单词前后用一些空格字符隔开。返回字符串中最后一个单词的长度。单词是指仅由字母组成、不包含任何空格字符的最大子字符串。
题目归纳：
无。

解题思路：
(1) 库函数法。return len(s.split()[-1])，split()默认以空格分词
(2) 手动遍历法。

Python3

class Solution:
    def lengthOfLastWord(self, s: str) -> int:
        # 二、手动遍历
        # 摒弃遍历一定是从左到右的想法，开阔思路，可以反向遍历解决的就反向遍历

        last_word_len = 0
        reverse_index = len(s) - 1
        # (1)跳过字符串末尾空格
        while (s[reverse_index] == ' '):
            reverse_index -= 1
        # (2)遍历最后一个单词
        while (reverse_index >= 0 and s[reverse_index] != ' '):
            last_word_len += 1
            reverse_index -= 1
        return last_word_len
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

19. 最长公共前缀

题目链接：最长公共前缀 - leetcode
题目描述：
编写一个函数来查找字符串数组中的最长公共前缀。如果不存在公共前缀，返回空字符串 ""。
题目归纳：
无。

解题思路：
(1) 逐列比较法，也可以叫做纵向扫描。时间复杂度 $O (mn)$ ，空间复杂度 $O (1)$
(2) 按字典序排序后，比对字符串0与字符串i-1的最长前缀。用数学中的夹逼定理类比。

Python3

纵向扫描

class Solution:
    def longestCommonPrefix(self, strs: List[str]) -> str:
        # 纵向扫描法
        
        # 防御性编程，特例值判断
        if strs is None:
            return ""
        
        compare_length = len(strs[0]) # 所要比较的字符串长度
        strs_length = len(strs)       # 字符串数组长度

        for j in range(0, compare_length): # 在编程习惯中，j一般作为列
            ch = strs[0][j] # 第j列字符
            for i in range(1, strs_length):# 0已经取过了，从1开始，对比数组中的每个字符串
                if ( len(strs[i]) > j and strs[i][j] is ch ): # 前缀相同，继续比对
                    continue
                else: # 比对终止
                    return strs[0][0:j]
        
        return strs[0]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

字典序排序+纵向比较

class Solution:
    def longestCommonPrefix(self, strs: List[str]) -> str:
        res = ''
        strs.sort() # 字典序排序
        start = strs[0]
        last = strs[-1]
        for i in range(min(len(start), len(last))):
            if start[i] != last[i]:
                return res
            res += start[i]
        return res
1
2
3
4
5
6
7
8
9
10
11

19. 反转字符串中的单词

题目链接：反转字符串中的单词 - leetcode
题目描述：
给你一个字符串 s ，请你反转字符串中单词的顺序。单词是由非空格字符组成的字符串。s 中使用至少一个空格将字符串中的单词分隔开。返回单词顺序颠倒且单词之间用单个空格连接的结果字符串。注意：输入字符串 s 中可能会存在前导空格、尾随空格或者单词间的多个空格。返回的结果字符串中，单词间应当仅用单个空格分隔，且不包含任何额外的空格。
题目归纳：
无。

解题思路：
(1) 得到以’ '为分词依据的分词词组
(2) 原地对称置换
(3) 返回加入空格的结果

Python3

class Solution:
    def reverseWords(self, s: str) -> str:
        # 一、得到以' '为分词依据的分词词组
        strs = s.split()

        # 二、原地对称置换
        start = 0
        end = len(strs) - 1
        while start < end:
            strs[start], strs[end] = strs[end], strs[start]
            start += 1
            end -= 1
        
        # 三、返回加入空格的结果
        return " ".join(strs)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

20. 找出字符串中第一个匹配项的下标(KMP求解)

题目链接：找出字符串中第一个匹配项的下标 - leetcode
题目描述：
给你两个字符串 haystack 和 needle ，请你在 haystack 字符串中找出 needle 字符串的第一个匹配项的下标（下标从 0 开始）。如果 needle 不是 haystack 的一部分，则返回 -1 。
题目归纳：
hay是干草，haystack是干草堆，needle是针。所以这道题可以翻译成英文Looking for a needle in a haystack，即大海捞针。这是打趣的说法，事实上，这道题就是字符串的模式匹配，不如我们写一个KMP算法，数据结构的痛苦又回来了？请看这个视频《最浅显易懂的 KMP 算法讲解》—— 奇乐编程学院，KMP的细节我不赘述了，在代码的关键部分我会注释。

解题思路：
(1) 调包侠。return haystack.find(needle)
(2) 手写字符串模式匹配算法。

class Solution:
   def build_next(self, pattern: str):
       next = [0] * len(pattern) # next[i]表示：pattern[0 ... i]子串，共同前后缀的长度。在kmp中有一句j=next[i]，故next[i]也可以理解为跳过匹配的个数
       prefix_len = 0 # 当前共同前后缀的长度
       i = 1
       while i < len(pattern):
           if (pattern[prefix_len] == pattern[i]): # 前后缀部分比对成功
               prefix_len += 1
               next[i] = prefix_len
               i += 1
           else:
               if prefix_len == 0: 
                   next[i] = 0
                   i += 1
               else:
                   prefix_len = next[prefix_len - 1] # 利用之前存储的信息,更新共同前后缀长度,避免重新匹配计算
       
       return next

   def kmp(self, s: str, pattern: str):
       next = self.build_next(pattern)

       i = 0 # 主串指针
       j = 0 # 匹配串指针

       while i < len(s): # 遍历主串
           if s[i] == pattern[j]: # 字符匹配，指针后移
               i += 1
               j += 1
           elif j > 0: # 字符失配，但根据next数组，跳过前面一些匹配上的字符，避免重头开始
               j = next[j-1]
           else: # 这种情况是j=0，说明匹配串pattern第一个就没匹配上
               i += 1
           
           if j == len(pattern): # 匹配完成
               return i - len(pattern)

       return -1


   def strStr(self, haystack: str, needle: str) -> int: 
       # 写一个kmp算法
       return self.kmp(haystack, needle)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

21. 文本左右对齐

题目链接：文本左右对齐 - leetcode
题目描述：
题目较长，直接看链接中的描述。
题目归纳：
这道题是有实际用途的，比如窗口宽度调整了，那文本展示自然也要跟着变，学会了这道题，就掌握了记事本的一个技术组件。
解题思路：

def blank(n: int) -> str:
    return ' ' * n

class Solution:
    def fullJustify(self, words: List[str], maxWidth: int) -> List[str]:
        # (1)重新排版单词，使其每行恰好有 maxWidth 个字符，且文本的左右两端必须对齐
        # (2)尽可能地往每行中 多 放置单词，必要时可使用空格 ' '填充，使每行恰好有 maxWidth 个字符
        # (3)尽可能均匀分配单词间的空格数量，若空格' '不能均匀分配，则左侧放置的空格数要多于右侧的空格数
        # (4)文本的最后一行左对齐，单词之间不插入额外的空格。也就是说最后一行的单词之间只能有一个空格，其余空格都在末尾。


        # (1)一行应该至少满足：该行单词长度之和 + 空格长度 = maxWidth。单词之间的空格数avgSpaces = numSpaces / (numWords-1)
        # (2)若不满足条件(1)，则要分行
        # (3)先把每一行是哪些单词确定下来，然后再填充空格。和题解思路一样

        # new_words = [ [] for _ in range(0, len(words))] # 考虑最坏的情况，即每个单词长度都是maxWidth，所以要开辟n个数组
        ans = []
        right, n = 0, len(words)
        while True: # 由于是一次性遍历，还不确定words中每个单词的长度，所以用死循环，达到条件后再退出
            left = right # 当前行第一个单词，在words的位置。双指针写法。
            sumLen = 0 # 归零。该行单词长度之和
            
            # (1)循环确定当前行可以放多少单词。right - left 是空格个数，因为单词之间至少有一个空格
            while right < n and (sumLen + len(words[right]) + (right - left)) <= maxWidth:
                sumLen += len(words[right])
                right += 1
            
            # (2)当前行是否是最后一行。单词左对齐，且单词之间应该只有一个空格，行末填充剩余空格。越特殊的情况越要提前判断，就像冒泡点击一样。
            if right == n:
                last_line = " ".join(words[left:])
                ans.append(last_line + blank(maxWidth - len(last_line)))
                break # 结束
            
            numWords = right - left
            numSpaces = maxWidth - sumLen
            # (3)当前行只有一个单词：则该单词左对齐，只需要在行末填充剩余空格。
            if numWords == 1:
                line = words[left] + blank(numSpaces)
                ans.append(line)
                continue # ？
            
            # (4)当前行不只一个单词。
            avgSpaces = numSpaces // (numWords - 1)
            extraSpaces = numSpaces % (numWords - 1)
            s1 = blank(avgSpaces + 1).join(words[left: (left+ extraSpaces+1)]) # 拼接额外加一个空格的单词
            s2 = blank(avgSpaces).join(words[(left+ extraSpaces+1): right]) # 拼接剩余单词
            ans.append(s1 + blank(avgSpaces) + s2)
        
        return ans
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49

附加题

1. 买卖股票的最佳时机Ⅲ

该题不在面试经典 150 题中，作为补充。

题目链接：买卖股票的最佳时机Ⅲ - leetcode
题目描述：
给定一个数组，它的第 i 个元素是一支给定的股票在第 i 天的价格。设计一个算法来计算你所能获取的最大利润。你最多可以完成两笔交易。注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。
题目归纳：
与Ⅱ的区别：最多可以完成两笔交易，这意味着状态的增多，用动态规划解法，也意味着状态转移方程的函数关系增多。第Ⅱ题只考虑，当天手上结束时有无股票，可以认为第Ⅱ题是这道题的一种特殊情况，实际上你拿这道题的代码去跑第二题也是完全可以的，只是要稍作修改，拿掉一笔交易操作，且return sell2。

Python3

动态规划法

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        # 这道题与二的区别是，可以 最多完成两笔交易，但不能同时参与多笔交易（必须在再次购买前出售掉之前的股票），而且同一天不能既买又卖，所以相当于是在一的基础上，加了可以完成 两笔交易 的条件
        # 动态规划解法
        
        # 1.列出状态。未进行过任何操作的利润显然为 0，因此可以不用记录
        # buy1  只进行一次买操作，所获得的最大利润
        # sell1 只进行一次买和卖操作，所获得的最大利润
        # buy2  完成了第一笔交易后，只进行一次买操作，所获得的最大利润
        # sell2 完成了第一笔交易后，只进行一次买和卖操作，所获得的最大利润
        
        # 2.列出状态转移方程。转移方程重点在于: 状态与状态转移函数，列状态是第一步，列状态之间的转移函数是第二步。在同一天买入并且卖出的收益为零。
        # buy1 = max(buy1, -prices[i]) 不进行买卖操作，or，买入价格为prices[i]的股票
        # sell1 = max(sell1, buy1 + prices[i])
        # buy2 = max(buy2, sell1 - prices[i])
        # sell2 = max(sell2, buy2 + prices[i])
        
        # 3.列出状态初值。
        # buy1 = -prices[0]
        # sell1 = 0
        # buy2 = sell1 - prices[0] = -prices[0]
        # sell2 = 0

        # 4.开始从初值边界以外进行动态规划，由于维护的是最大值，且sell1与sell2初值为0，故sell1与sell2最终一定大于等于0

        # 正式代码
        n = len(prices)

        buy1 = -prices[0]
        sell1 = 0
        buy2 = -prices[0]
        sell2 = 0

        for i in range(1,n):
            buy1 = max(buy1, -prices[i]) # 不进行买卖操作，or，买入价格为prices[i]的股票
            sell1 = max(sell1, buy1 + prices[i])
            buy2 = max(buy2, sell1 - prices[i])
            sell2 = max(sell2, buy2 + prices[i])
        return sell2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

# 对第二题的通用解法
class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        n = len(prices)
        buy1 = buy2 = -prices[0]
        sell1 = sell2 = 0
        for i in range(1, n):
        	# 第一笔交易要被拿掉
            # buy1 = max(buy1, -prices[i])
            # sell1 = max(sell1, buy1 + prices[i])
            buy2 = max(buy2, sell2 - prices[i]) # sell1改sell2
            sell2 = max(sell2, buy2 + prices[i])
        return sell2
1
2
3
4
5
6
7
8
9
10
11
12
13

2. 买卖股票的最佳时机Ⅳ

该题不在面试经典 150 题中，作为补充。

题目链接：买卖股票的最佳时机Ⅳ - leetcode
题目描述：
给你一个整数数组 prices 和一个整数 k ，其中 prices[i] 是某支给定的股票在第 i 天的价格。设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。也就是说，你最多可以买 k 次，卖 k 次。注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。
题目归纳：
与Ⅱ的区别：与第三题只能买卖2次，这道题给定了买卖次数，最多只能买卖k次，进一步扩大了题目的适用范围。

Python3

动态规划法

class Solution:
    def maxProfit(self, k: int, prices: List[int]) -> int:
        # 与第三题只能买卖2次，这道题给定了买卖次数，最多只能买卖k次，进一步扩大了题目的适用范围。
        # 动态规划解法，与第二题的buy1, sell1, buy2, sell2不同，这里只要使用数组来表达buy1, sell1, buy2, sell2 ..., buyj, sellj...
        # 如：
        # buy_sell[j][0] 表示buyj, 1 <= j <= k
        # buy_sell[j][1] 表示sellj, 1 <= j <= k

        n = len(prices)
        buy_sell  = [[0 for k in range(0,2)]for j in range(0, k+1)] # 生成动态转移数组
        
        # 赋初值
        buy_sell[0][0] = 0
        buy_sell[0][1] = 0
        for j in range(1, k+1):
            buy_sell[j][0] = -prices[0]
            buy_sell[j][1] = 0

        # 动态规划
        for i in range(1,n):
            for m in range(1, k+1):
                buy_sell[m][0] = max(buy_sell[m][0], buy_sell[m-1][1] - prices[i])
                buy_sell[m][1] = max(buy_sell[m][1], buy_sell[m][0] + prices[i])

                # 将第二题代码放在这里，便于对照编程与记忆            
                # buy1 = max(buy1, -prices[i]) # 不进行买卖操作，or，买入价格为prices[i]的股票
                # sell1 = max(sell1, buy1 + prices[i])
                # buy2 = max(buy2, sell1 - prices[i])
                # sell2 = max(sell2, buy2 + prices[i])
        
        return buy_sell[k][1]
        # return sell2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

3. 买卖股票的最佳时机含手续费

该题不在面试经典 150 题中，作为补充。

题目链接：买卖股票的最佳时机含手续费 - leetcode
题目描述：
给定一个整数数组 prices，其中 prices[i]表示第 i 天的股票价格；整数 fee 代表了交易股票的手续费用。你可以无限次地完成交易，但是你每笔交易都需要付手续费。如果你已经购买了一个股票，在卖出它之前你就不能再继续购买股票了。返回获得利润的最大值。注意：这里的一笔交易指买入持有并卖出股票的整个过程，每笔交易你只需要为支付一次手续费。
题目归纳：
与Ⅱ的区别：与第三题只能买卖2次，这道题给定了买卖次数，最多只能买卖k次，进一步扩大了题目的适用范围。

Python3

动态规划法

class Solution:
    def maxProfit(self, prices: List[int], fee: int) -> int:
        # 只要获得的利润大于手续费就可以买卖，之前是最多只能交易k次，这里是交易次数无限了。这道题是第2题的升级版
        # 第2题的解法是动态规划算法
        # dp[i][0] 第i天未持有股票的最大收益
        # dp[i][1] 第i天  持有股票的最大收益
        n = len(prices)
        dp = [[0 for j in range(0,2)]for i in range(0, n+1)]
        
        # 天数跟随prices数组下标，从0开始
        dp[0][0] = 0
        dp[0][1] = -prices[0]
		
		# 第0天的初值已经有了，从第1天开始迭代遍历
        for day in range(1, n):
            dp[day][0] = max(dp[day-1][0], dp[day-1][1] + prices[day] - fee) # 卖出，只有卖出要付手续费，与买卖股票Ⅱ的唯一区别：有一个减去手续费的操作
            dp[day][1] = max(dp[day-1][1], dp[day-1][0] - prices[day]) # 买入，买入不需要付手续费
        
        return dp[n-1][0]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

动态规划(状态压缩)

可以发现，使用dp数组，有大量的元素用后即扔(n-1下标之前的元素)，再也没有使用过，这样会浪费内存空间，因此，如果只关心结果，不关心过程，可以考虑用变量把数组替换掉，之前是数组的一系列元素在迭代，现在是孤零零的变量在迭代而已。

使用状态压缩的前提。
(1) 只关心动态规划的结果，不关心过程中产生的值，即过程中用一次就不再访问，但对后续过程仍有影响的值。
(2) 关注内存空间的使用。
一个简单的例子：求数组中所有元素值之和。
for i in range(0, n): # 状态压缩前，sum[i]表示0...i之间所有元素之和
	if i == 0:
		sum[0] = nums[0]
	else:
		sum[i] += sum[i-1] + nums[i]
for i in range(0, n): # 状态压缩后，最终得到的结果只是数组全部的元素和，中间值在迭代过程中有用，对结果没用。
	Sum += nums[i]
1
2
3
4
5
6
7

class Solution:
    def maxProfit(self, prices: List[int], fee: int) -> int:
        # 只要获得的利润大于手续费就可以买卖，之前是最多只能交易k次，这里是交易次数无限了。这道题是第2题的升级版
        # 第2题的解法是动态规划算法
        # dp0 第i天未持有股票的最大收益
        # dp1 第i天  持有股票的最大收益
        n = len(prices)
        
        # 天数跟随prices数组下标，从0开始
        dp0 = 0
        dp1 = -prices[0]
		
		# 第0天的初值已经有了，从第1天开始迭代遍历
        for day in range(1, n):
            dp0 = max(dp0, dp1 + prices[day] - fee) # 卖出，只有卖出要付手续费，与买卖股票Ⅱ的唯一区别：有一个减去手续费的操作
            dp1 = max(dp1, dp0 - prices[day]) # 买入，买入不需要付手续费
        
        return dp0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

到这里，数组篇就全部刷完了，目前时间是12月14日下午五点半，之后记得多回顾复习。

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/花生_TL007/article/detail/459310

Leetcode面试经典150题刷题记录——数组 / 字符串篇

数组 / 字符串篇

1. 合并两个有序数组

Python3

排序法

双指针法

2. 移除元素

Python3

3. 删除有序数组中的重复元素

Python3

6. 轮转数组

Python3

解法一(新数组)

解法二(通过大部分测试用例，但仍旧存在超时)

解法三(原地翻转法)

7. 买卖股票的最佳时机

Python3

8. 买卖股票的最佳时机Ⅱ

Python3

贪心法

动态规划法

9. 跳跃游戏

Python3

动态规划

贪心法

10. 跳跃游戏Ⅱ

Python3

动态规划法

贪心法

11. H 指数

Python3

排序法

计数排序法

二分查找

13. 除自身以外数组的乘积

Python3

左右乘积列表

左右乘积列表(改进空间复杂度至 O ( 1 ) O(1) O(1))

14. 加油站

Python3

15. 分发糖果

Python3

16. 罗马数字转整数

Python3

17. 整数转罗马数字

Python3

18. 最后一个单词的长度

Python3

19. 最长公共前缀

Python3

纵向扫描

字典序排序+纵向比较

19. 反转字符串中的单词

Python3

20. 找出字符串中第一个匹配项的下标(KMP求解)

21. 文本左右对齐

附加题

1. 买卖股票的最佳时机Ⅲ

Python3

动态规划法

2. 买卖股票的最佳时机Ⅳ

Python3

动态规划法

3. 买卖股票的最佳时机含手续费

Python3

动态规划法

动态规划(状态压缩)

左右乘积列表(改进空间复杂度至 $O (1)$ )