- 1【AI OpenDevin】开源AI程序员,帮您写代码,开发程序_opendevin怎么使用
- 2sourceTree中git工作流使用_sourcetree git工作流不能用
- 3【计算机毕业设计】基于微信小程序的开发项目150套(附源码+演示视频+LW)
- 4【2024 信息素养大赛c++模拟题】算法创意实践挑战赛(基于 C++)_温州市信息素养提升实践活动计算思维项目c++作品
- 5【数据库&sql】EXISTS、NOT EXISTS、IN、NOT IN的分析及示例_sql 查询 not exists
- 6全网最全深度学习案例整理汇总
- 7【软件工程】建模工具之开发各阶段绘图——UML2.0常用图实践技巧(功能用例图、静态类图、动态序列图&状态图&活动图)_功能模块用uml拿个图
- 8【解决】报错:部署Deformable-DETR环境问题_no module named 'deformable_detr_ops
- 9EEPROM AT24C08的操作_at24c08 page addr
- 10FFmpeg音视频开发知识点(二)_avcodec_receive_frame -11
决策树(Decision Tree)
赞
踩
1. 决策树的基本概念
我们这里介绍一下一个比较简单的机器学习系统----决策树. 它的概念最容易理解, 因为人类的许多决策实际上就是一个决策树.
通常使用的分类回归树(class and regress tree)是一个二叉树。它的形式一般为:

每个方框代表一个节点. 每个非叶子节点有2个分支, 一个是判定True, 一个判定False. 分别走两个不同的分支. 叶子节点具有决策权. 任何一个输入从root出发, 总是会达到且唯一到达一个叶子节点. 这就是决策树的工作原理.
决策树有两种节点: 中间节点和叶子节点。 1. 每个中间节点有4个参数:
a) 判定函数。 是一个特征的取值。 当特征小于等于这个值得时候决策路径走左边, 当特征大于这个值得时候决策树走右边。
b) 不纯度值(impurity value). 是当前节点的不纯度值. 关于不纯度值得意义后面会讲到. 他反应了当前节点的预测能力.
c) 覆盖样本个数(n_samples). 是指参与此节点决策的样本个数. 父亲节点§和两个孩子节点(l,r)的样本个数的关系为: n_samples§ = n_samples(l) + n_samples® 覆盖样本个数越多, 说明判定函数越稳定. 实际上很容易看出来, 所有的叶子节点所对应的样本是总样本的一个划分.
d) 节点取值(node value). 节点取值是一个数组. 数组的长度为类目个数. value = [997, 1154] 表示在2151个样本数中, 有997个属于class1, 1154属于class2. (这是分类树的意义, 会归数的取值规则后面会讲.)
2. 每个叶子节点有3个参数. 除了没有决策函数之外, 其他参数意义一样.
2. 不纯度函数(impurity function)
决策树最重要的概念就是不纯函数(I)的概念. 当一个节点需要分割的时候, 实际上就是找到一个合适的特征的一个合适的取值作为阈值(thresh)进行分割. 那么问题来了, 怎么找到那个合适的特征的合适的取值呢? 主要的依据就是不纯度的变化(delta I). 首先我们给出不纯度函数的定义. 不纯度函数不是一个具体的函数, 它是满足一系列约束的函数的总称.
根据输出实例的取值范围不同. 决策树有不同的种类. 如果输出实例是离散的, 那么决策树是一个分类树; 如果输出实例是连续的, 那么决策树是一个回归树.如果决策树是分类树. 那么输出空间定义为输出实例所有取值的集合. 这个集合是有限集合. 不失一般性, 使用{1,…,k}这可个取值. 不纯度函数(I)的定义为:

每一项实际上就是属于类目ci的概率, 记为pi.
如上公式可以看出不纯度函数的定义域是长度为k的向量, 向量每个数的取值为0~1, 且加和为1. 第i个数是特征矩阵中属于类别i的特征向量个数在整个样本个数(n_sample)的占比.且必须满足如下约束: 1. 当所有样本都属于同一类时候I取最小值. 即I在点(1,0,…,0),(0,1,…,0), …, (0,…,0,1)取最小值.
2. 当样本中每个类目下样本个数相同时I取最大值. 即I在点(1/k,…,1/k)取最大值.
3. I对于定义域中每个取值p1,…,pk是对称的. 即I(p1, p2,…,pk) = I(p2,p1,…,pk)等. 从函数图像的角度理解, 就是函数一定是关于值坐标轴对称.
4. I必须是绝度凸函数(strickly concave)即设p和p’(注意这里是一个长度为k的向量)为定义域下两个可能的取值. 那么
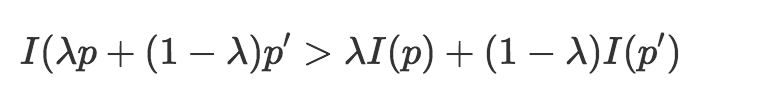
另外一个概念是不纯度变化(impurity reduction).
我们回到决策树的结构, 每个父节点的两个子节点都是对父节点的划分. 那么如何评价这次划分呢? 于是我们引入了不纯度变化(impurity reduction)的概念. 我们看着公式来理解:
考虑一般性我们设X1,X2…Xs是特征空间X的一个划分. 不纯度变化定义为:

这个公式很好理解,令s=2, 那么 X1,X2是对于原空间的一个划分. 按理说, 一个好的划分应该让不纯度变低, 以便让类目归属更加清晰. 公式后面一个累加和实际上就是这两个划分的不纯度的期望. 原不纯度减去划分后的不纯度的期望就是减少的不纯度的差值. 显然这个差值越大说明划分让子节点的纯度更"纯".
另外, 需要强调一点, 根据不纯度函数的第三个约束, 即不纯度函数是定义域下的凸函数, 可以保证不纯度变化(impurity reduction) 大于等于0.当且仅当所有划分的样本数相当取0.
可这么说, 分类决策树节点划分的依据是找到一个特征的一个取值, 根据这个划分是的不纯度缩减量最大.
下面我们介绍两个常用不纯度函数, 信息熵(info entropy)和基尼指数(gini index).
2.1 信息熵(info entropy)
首先介绍一下信息熵的概念. 我们把样本抽取过程当做一次随机试验A, 那么A有k个可能的输出A1,A2,…,Ak . 对应于k个分类. 那么A的信息熵定义为:
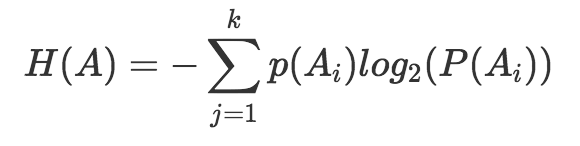
信息熵满足不纯度函数的定义. 所以我们定义:
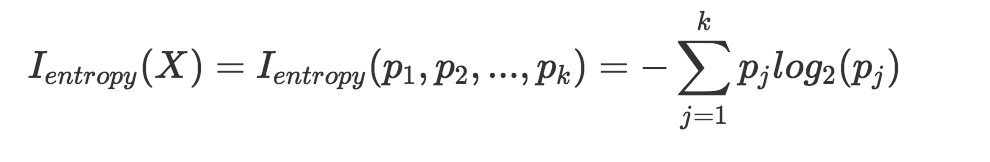
把这个不纯度函数的定义带入到不纯度函数的公式中就可以得到相应的不纯度变化函数.
这个函数很出名, 我们把它写出来(后面的基尼指数就不写了.)

按照教课书的习惯, 当不纯度函数为信息熵时不纯度变化又叫做信息增益(info gain).
2.2 基尼指数(Gini Index)
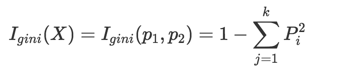
这里强调一下不管是信息熵还是基尼指数, 他们都是不纯函数的一种表达, 不纯度变化的计算没有任何变化. 我们也可以自己撰写不纯度函数. 当k=2时候, 我们可以吧信息熵和基尼指数在二维坐标上图形画出来.

可以看出来这两个方法的区别很小. 实际过程中使用哪个方法作为不纯度函数效果不会有太大变化.
我们现在了解了分类决策树在每次分割过程中如何评价分割的好坏, 一遍每次找到最佳分割点. 下面我们继续介绍回归树是如何定义不纯度函数的.
3. 回归树
我们考虑一下会归树的构建过程. 当决策树只有一个节点的时候(root节点), 这个节点包含所有待测试样本. 如果我们需要选择一个数来预测函数的取值, 我们会选哪个? 由于我们没有任何多余的信息, 根据最大似然原则, 我们取所有样本取值的均值, 作为预测值.
同样的道理随着决策树的建立, 所有的叶子节点是root节点的一个划分. 每个叶子节点都充当一个预测器的角色. 每个叶子节点的预测值是每个节点包含的样本取值的均值.
那么对于回归决策树来说, 我们的任务是如何有效的划分让每个叶子节点更具有代表性. 如果让一个叶子节点更具有代表性, 我们直观的感受是这个节点的样本都趋同于均值(期望), 实际上就是方差较小. 这正是回归决策树不纯度函数的定义的理论依据.
对于给定的训练集:
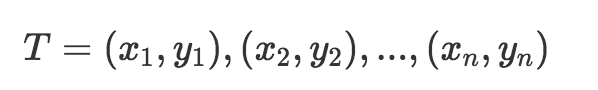
Y是连续变量. 考虑如何生成回归树.考虑一颗分类树, 每个叶子节点都对应一组概率值, 表示达到这个叶子节点的样本分到每个类目下的概率. 回归树基本结构和分类数一样, 不同的是每个叶子节点都表示对于到达这个叶子节点的样本的预测值(f(x)). f(x)等于这个叶子节点所有输入实例xi对应的输出yi的均值.有的叶子节点是对样本的一个划分R1, R2, …, Rm
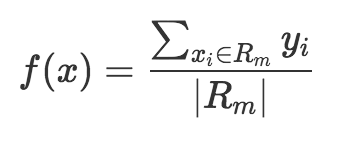
举个例子:
这颗回归树是对抛物线y=1-x^2 ( -1 < x < 1)模拟, 我们把原函数和预测函数画在同一个坐标系统.
我看观察图形可以看出, 回归树的特点是使用连续的折线来拟合曲线. 因为在每个叶子节点的取值是固定的, 而这颗回归树只有8个叶子节点.
回归树的构建和分类数构建方法类似. 同样是需要找个一个划分, 使得不纯函数的缩减最大. 但是上面所介绍的不纯度函数是根据分类树定义的. 我们需要定义适应回归树的不纯度函数.
在回归树中每个非叶子节点都是样本空间的一个子集的处理单元. 某个子集为Xm每个样本x有2个属性, 一个是实际输出y, 另一个是预测输出hat(y). 上面介绍过hat(y)是通过这个节点下所有y的均值算出来的, hat(y)这个节点下所有y的期望. 反应的是总体上的拟合程度. 那么另外一个衡量集合稳定性的指标是方差, 它衡量hat(y)的代表性. 方差越小, 说明hat(y)越具有代表性. 因此我们可以定义一种不纯度函数, 就是这个节点下输出值的方差.
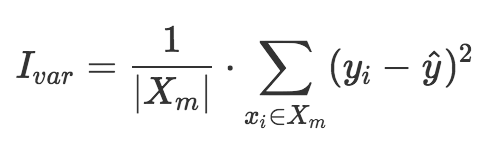
这种方法又叫做"最小二乘法". 同样的带入不纯度变化的公式, 经过必要的化简我们得到:
值得注意的是, 公式中有2处对于当前节点来说是常数. 只有最小二乘有实际意义. 我们最大化不纯度变化, 就是最小化最小二乘函数.
一般的教科书直接写成这样的公式:
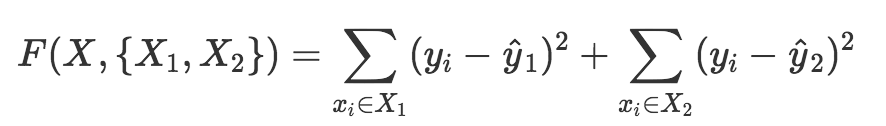
在本文中我们给出一个符合不纯度函数定义的解释. 这样保证回归树和决策树在实现上是统一的.
4. 小结
上面介绍了决策树一个重要概念, 不纯函数. 不纯函数不仅是分类树的概念, 也是回归树的概念. 它们在形式上是统一的. 这点很有意义, 下面我们分析sklearn源码时候可以发现, 在设计决策树时候没有区分分类和回归树, 他们的不同都被封装在不纯函数的定义和计算节点的输出中了.
5. 决策树的构建
上面一章介绍了分类和回归树在某个节点如何选择合适的特征和特征取值进行分裂. 这一章介绍决策树的构建方法, 即如何决定每步应该分裂的节点. 决策树的构建一般有2种方法: 1. 深度优先
2. 广度优先
| 名称 | 图像 | 说明 |
|---|---|---|
| 广度优先 |  | 广度优先按照层次来构建树的. 首先根据合适的不纯度函数来分裂root成2个节点; 然后依次分裂第二层的2个节点; 依次递推. |
| 深度优先 |  | 深度优先采用递归的思想, 在每个节点都是优先有左边的子树建好, 再建右边子树 |
不管是深度优先还是广度优先, 决策树算法都需要知道什么时候一个节点应该作为叶子节点. 如果没有约束决策树会一直建设下去知道节点只有一个类目(或者只有一个取值)才停止. 这样会导致决策树变得非常庞大, 引发过拟合问题.
一般来说, 当如下条件其中之一满足的时候, 当前节点停止构建, 作为决策树的叶子节点.
| 参数 | 意义 | 终止条件 |
|---|---|---|
| min_samples_split | 当前节点允许分裂的最小样本数 | 当前节点样本数小于这个值时候 |
| min_samples_leaf | 叶子节点最少样本数 | 任何分裂不能导致子节点的样本数小于此值, 否则禁止分裂 |
| min_impurity_split | 分裂的不纯度阈值 | 当前节点不纯度小于此值时不分裂 |
| max_path | 数的最大深度 | 当前节点的深度大于等于此值是不分裂 |
这些控制条件可以控制数的规模, 因为根据不纯度变化的定义, 将所有的节点都放在唯一的叶子节点(这样每个叶子节点不纯度都是0)中不纯度变化最大. 这显然不是我们想要的.
6. 决策树的预测
通过上述的说明, 决策树的预测就非常的简单了. 决策树中只有叶子节点有预测功能. 一个测试样本从root出发选择正确的路径, 一定会走到一个叶子节点. 叶子节点的值即为决策树对这个样本的预测.
1、如果是分类树. 叶子节点给出每个类别的占比. 概率最大的类别作为这个叶子节点的预测值. 其概率值为置信度.
2、如果是回归树. 叶子节点的所有样本的输出的平均值作为这个测试样本的预测值.
7. sckit-learn 决策树源码分析
本文的结构实际上就是按照sckit-learn中的决策树进行设计的. 源代码在: https://github.com/scikit-learn/scikit-learn/tree/master/sklearn/tree . 首先介绍一下主要文件:
criterion.py*
criterion.py* 主要定义了各种不纯度函数及其计算和转化方法.
| 主要类 | 功能描述 |
|---|---|
| abstract Criterion | 定义一系列计算某个不纯度或者不纯度缩减的方法1. node_impurity: 计算当前节点的不纯度2. children_impurity: 计算2个子节点的不纯度3. impurity_improvement: 计算当前节点的不纯度缩减量4. proxy_impurity_improvement: 由于当前节点的不纯度是一个常数, 因此在比较不纯度缩减量时候有更加简单的方法, 这个方法在分裂过程中最常用, impurity_improvement仅当需要计算不纯度缩减绝对值时才用5. node_value: 当前节点的值, 用于预测. 当决策树是分类树时它计算每个类目的概率, 当决策树是回归树是, 计算所有样本输出的均值, 作为输出值 |
| Class ClassificationCriterion | 继承 Criterion; 重写node_value方法, 适应分类树的计算 |
| Class Entropy | 继承ClassificationCriterion; 重写impurity各个方法, 符合entropy的定义 |
| Class Gini | 继承ClassificationCriterion; |
| Class RegressionCriterion | 继承 Criterion; 重写node_value方法, 适应回归树的计算 |
| class MSE | 继承 RegressionCriterion主要实现上文提到回归树的不纯度计算方法 |
Splitter.py*
splitter.py* 主要解决一些工程性的问题. 根据不纯度算法的要求, 我们要在每个节点遍历所有特征的所有取值. 在性能角度需要考虑:
- 如果某个特征取值是连续的, 是否一定需要遍历所有取值? 如果相邻的取值差距很小是否可以直接跳过?
- 有没有一些折中的方案是速度和质量的折中? 比如一些随机算法?
| 主要类 | 功能描述 |
|---|---|
| Abstract Splitter | 抽象类, 定义分割需要的基本方法 |
| class BestSplitter | 继承Splitter 最优质的分割方法, 每次分割几乎遍历所有所有特征的所有取值, 但是为了加速, 有一个叫step的参数, 如果相邻的两个取值间隔小于step就直接忽略 |
| class RandomSplitter | 继承Splitter 采用随机算法没有遍历特征的所有值, 一般都是使用BestSplitter |
_tree.py*
这个文件是讲所有的功能拼装在一起形成一个可以独立使用决策树类. 首先它声明了一个TreeBuilder的系列类, 用于实现前文所说的深度优先建树和广度优先建树.
tree.py
这是源代码中为唯一一个python文件(其他都是cython文件). 他主要封装了_tree.py* 定义和主流机器学习库兼容的方法体系.
8. 实例
本章, 我们给出一个完整的实例.这个例子很简单, 但是我们还是可以发现参数调整对于决策树质量的重要性.
import numpy as np from sklearn.tree import DecisionTreeRegressor import matplotlib.pyplot as plt # Create a random dataset rng = np.random.RandomState(1) X = np.sort(5 * rng.rand(80, 1), axis=0) y = np.sin(X).ravel() y[::5] += 3 * (0.5 - rng.rand(16)) # Fit regression model regr_1 = DecisionTreeRegressor(max_depth=2) regr_1.fit(X, y) # Predict X_test = np.arange(0.0, 5.0, 0.01)[:, np.newaxis] y_1 = regr_1.predict(X_test) # Plot the results plt.figure() plt.scatter(X, y, c="k", label="data") plt.plot(X_test, y_1, c="g", label="max_depth=2", linewidth=2) plt.xlabel("data") plt.ylabel("target") plt.title("Decision Tree Regression") plt.legend() plt.show()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
这个实例很简单. 首先需要使用DecisionTreeRegressor来声明一个回归树. 然后使用fit来训练, 最后使用predict来预测结果.
图像中我们看到有点欠拟合, 我们加大max_depth=3和max_depth=5

我们看出来max_depth=5就已经有点过拟合. 但是我们对max_depth=3还有有点不满意.
我们进一步改进, 维持max_depth=5不变, 增加min_samples_leaf=6的参数. 效果进一步提升.
可以看到参数对于决策树的质量来说非常重要.
同时我们注意到在0附近不管设置什么参数预测效果都很差. 这是由回归树的性质决定的. 回归决策树对于稀疏的数据的预测效果是非常差的. 我们从不纯度函数的定义就可以理解. 不纯度函数是一个叶子节点的方差, 要求方差尽可能小, 这样越是比较趋同的样本越容易被分到同一个节点内, 导致本来就稀疏的节点更加稀疏, 稀疏点附近的均值根本就没有代表性.
9. 决策树的深度思考
为什么决策树不需要数据归一化?
一般来说, 机器学习都需要特征归一化, 目的是让特征之间的比较可以在同一个量纲上进行. 但是从数据构建过程来看, 不纯函数的计算和比较都是单特征的. 所有决策树不需要数据的归一>化. 但是有点需要注意, 从上文中对splitter的源码分析中可以看出, 决策树为了加速遍历没有真正遍历所有取值, 当特征的绝对值太小的时候会导致相邻值的间隔小于step, 因此尽量让特征值不要太小(大于0.01比较保险).
如何正确的选择不纯度函数?
在gini函数小节中我们比较了gini和entroy在两元下的图形. 可以看到基本上没有区别. 有研究表明不同的不纯度函数对决策树产生的影响在2%以内1.
事实上很少有实际案例说明选择不纯度函数有显著的作用. 所以对于分类决策树选择gini, 对于回归选择MSE, 这样的默认配置可以满足绝大多数的需求.
决策树哪些参数最重要?
决策树的重要参数都是防止过拟合的. 我认为2个参数一定要设置:
1、min_samples_leaf 这个sklearn的默认值是1. 经验上必须大于100, 如果一个节点都没有100个样本支持他的决策, 一般都被认为是过拟合.
2、max_path 这个参数控制树的规模. 决策树是一个非常直观的机器学习方法. 一般我们都会把它的决策树结构打印出来观察, 如果深度太深对于我们的理解是有难度的. max_path也是防止过拟合的有效手段.
决策树为什么选择二叉树?
我们回到不纯度函数变化公式的本身:

我们假设决策树每个节点可以有多个子树. 举个极端的例子, 某一个特征的所有取值都不相同, 那么可以找到一个划分方法(只要足够多的子树)可以让每个子树都有唯一的类别. 那么此时公式的后半段为0. 这样不纯度变化取到最大值. 很明显这是一个算法上的偏见, 已经形成了过拟合.
但是如果是二叉树就可以有效的避免这个问题. 他迫使特征有多个取值这样的优势无效.
决策树的局限性有哪些?
决策树的主要问题是容易形成过拟合. 如果我们通过各种剪枝和条件限制, 虽然可以避免过拟合, 但是会牺牲特征的有效性. 举个例子:
1、样本有1w个测试记录
2、feature的数量是1k个
3、为了保证模型的有效性, 规定每个叶子节点包含的最少样本数为100
在构造决策树的过程中我们可以断言节点个数不会超过100个, 这样很多feature不仅没有多次分裂, 甚至有些特征根本无法参与决策.
为了解决决策树一系列的问题(这里不一一列举), 统计学家不再深入决策树的结构而是提出另外一个思路: 能够通过构造不同的简单的决策树共同决策? 这有点"三个臭皮匠顶一个诸葛亮"的感觉. 我会在下一个文章具体介绍一下这个方法, 即随机森林. 它是一个更加有效和常用的机器学习算法.
1、http://www.quora.com/Machine-Learning/Are-gini-index-entropy-or-classification-error-measures-causing-any-difference-on-Decision-Tree-classification ↩




