花生_TL007

这个屌丝很懒，什么也没留下！

热门标签

Opencv_13 图像滤波(低通滤波图像平滑去噪)_opencv低通滤波

作者：花生_TL007 | 2024-02-09 18:06:38

踩

opencv低通滤波

文章目录

一. 图像滤波简介

① 为什么图像是波?

我们都知道,图像由像素组成.下图是一张400 * 400的图片,一共包含了16万个像素点.

每个像素的颜色,可以用红绿蓝表示,大小范围是0~255.
如果把每一行所有像素(上例是400个)的红,绿,蓝的值,依次画成三条曲线,六得到下面的图形:

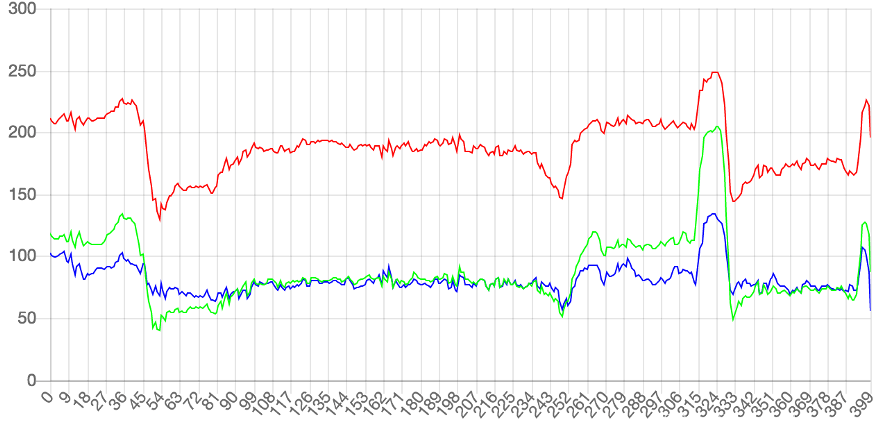
可以看到每条曲线都在不停地上下波动.有些区域波动比较小,有些区域波动不叫大,比如54,和324这两个点,然后对比一下图像,就可以看到曲线波动较大的地方,也就是图像出现突变的地方

这说明波动和图像是紧密关联的.图像本质上就是各种色彩波的叠加.

② 图像的频率

图像就是色彩的博定,波动大,就是色彩急剧变化.波动小,就是色彩平滑过渡.色彩剧烈变化的地方,就是图像的高频区域,色彩稳定平滑的地方,就是低频区域.

③ 滤波器

滤波: 就是从混合在一起的诸多信号中提取出来所需要的信号

低通滤波器: 减弱或者阻隔高频信号,保留低频信号
高通滤波器: 减弱或者阻隔低频信号,保留高频信号

在图像处理或者计算机应用中,在正式的图像进行分析处理之前需要一个预处理的过程.
预处理就是对图像作一些诸如降维,降噪的操作,主要是为了得到一个体积合适,只包含所需要的信息的图像,通常会用到一些滤波处理手法.滤波,实际上就是信号的处理,而图像本身可以看作是一个二维信号,其中像素点灰度的高低代表信号的强弱.对应高低频的意义:

高频: 图像灰度变化强烈的点,一般是轮廓或者是噪声
低频: 图像中平坦的,灰度变化不大的点,图像中的大部分区域.

而根据图像的高频和低频的特征,可以设计相应的高通和低通滤波器,高通滤波器可以检测图像中尖锐,变化明显的地方,而低通滤波器可以让图像变得平滑,滤除图像中的噪声.Opencv提供的低通滤波器有线性的均值滤波,方框滤波,高斯滤波器,非线性的双边滤波器,中值滤波器.高通滤波有基于Canny,Sobel,Scharr算子的各种滤波.有时候低通滤波和高通滤波其实是矛盾的,很多的时候边缘检测需要通过低通滤波降噪,然后通过高通滤波找到边缘,这里就需要调节参数在保证高频边缘不丢失的前提下尽可能多的去处理图像的噪声.

二. 低通滤波之线性滤波

线性滤波分为如下几种:

方框滤波
均值滤波
高斯滤波

什么是邻域算子:

利用给定像素周围的像素值决定次像素的最终输出值的一种算子

线性滤波:

一种常用的邻域算子,像素输出值取决于输入像素的加权和.

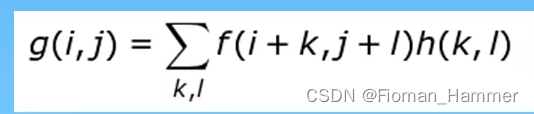
总结:
线性滤波器输出像素g(i,j)是输入像素f(i+k,j+l)的加权和,其中h(k,l)我们称为核,是滤波器的加权系数,上面的式子简写为:

中间的那个符号就是卷积的符号

① 方框滤波

函数原型:

void boxFilter( InputArray src, OutputArray dst, int ddepth,
                             Size ksize, Point anchor = Point(-1,-1),
                             bool normalize = true,
                             int borderType = BORDER_DEFAULT );

1
2
3
4
5

参数解释:

src: 输入图像
dst: 输出图像
ddepth: 输出图像的深度,-1代表使用原图像的深度,即src.depth()
ksize: 表示内核大小,一般使用Size(w,h)表示内核大小,Size(3,3)表示3*3的核大小
anchor: 表示锚点(即被平滑的那个点),默认值Point(-1,-1)表示锚点是核中心
normalize: 是否进行归一化处理.如果为true,就变成了均值滤波器.
borderType: 边界填充方式

方框滤波用到的核:

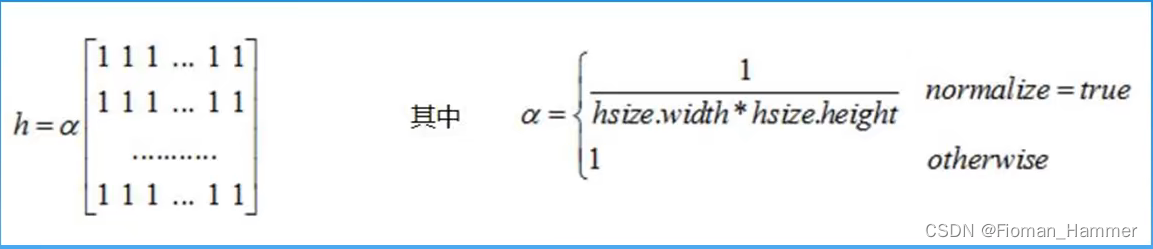
当normalize为true的时候,方框滤波就变成了均值滤波.归一化的目的就是让要处理的量压缩到一定的范围,其实就是将原来的像素值加权平均之后还是0~255

#include "MyOpencv.h"

int main(void)
{
	Mat original = imread("test_10.bmp", IMREAD_GRAYSCALE);
	imshow("Original", original);
	// 使用归一化的方框滤波器
	Mat dst;
	boxFilter(original, dst, -1, Size(3, 3));
	imshow("BoxFilterNormalize", dst);

	// 不适用归一化的滤波器,其实就是像素的累加
	boxFilter(original, dst, -1, Size(3, 3), Point(-1, -1), false);
	imshow("BoxFilterNoNormalize", dst);


	waitKey(0);

	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

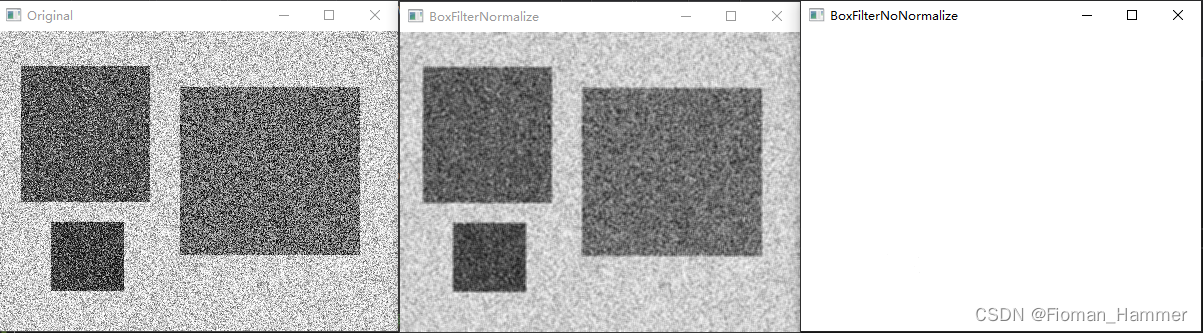
在这里插入图片描述

② 均值滤波

均值滤波使用的核:
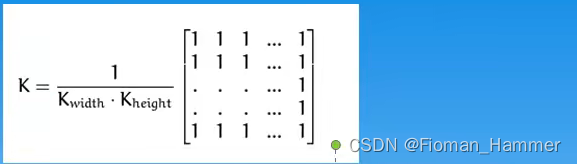
在这里插入图片描述
均值滤波就是方框滤波的归一化特例,就是用邻域内像素均值来代替该点的像素值,均值滤波在去噪的同时也破坏了图像的细节部分.

函数原型:

void blur( InputArray src, OutputArray dst,
                        Size ksize, Point anchor = Point(-1,-1),
                        int borderType = BORDER_DEFAULT );
1
2
3

参数解释:

src: 输入图像
dst: 输出图像
ksize: 滤波核大小
anchor: 锚点
boardType: 边界填充方式

#include "MyOpencv.h"

int main(void)
{
	Mat original = imread("test_11.bmp", IMREAD_GRAYSCALE);
	if (original.empty())
	{
		cout << "图像是空!" << endl;
		return 0;
	}
	imshow("Original", original);

	Mat dst;
	blur(original, dst, Size(5, 5));

	imshow("Blured", dst);

	waitKey(0);
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

结果:

均值滤波会让整个图像看起来更均化一些,但是也会丢失一些图像的细节

③ 高斯滤波

高斯滤波(Gauss Filter)是线性滤波中的一种.在Opencv图像滤波处理中,高斯滤波用于平滑图像,或者说是模糊图像,高斯滤波也是一种低通滤波器.

高斯滤波的思想就是:图像上的每个像素点的值,由其本身和邻域内其他的像素点的值经过加权平均后得到.只是这个核,是根据高斯分布求的.其中中心点是这个像素点本身,整个核的值服从高斯分布.

高斯函数:
高斯滤波,顾名思义,就是建立在高斯正态分布基础上的滤波器.
一维高斯函数:G(x)跟sigma的取值有极大的关系.sigma取值越大,图像越平缓,sigma取值越小,图像越尖锐.

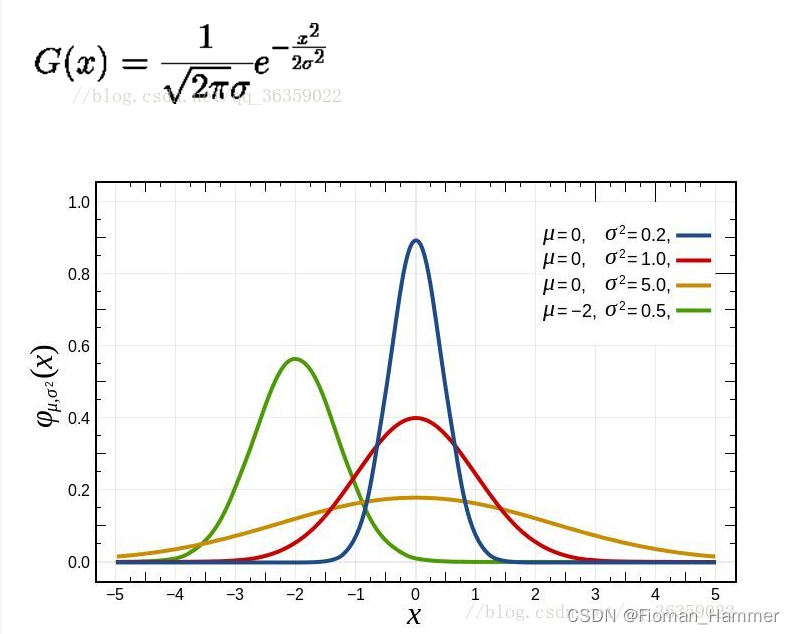
要理解高斯模糊,首先要明白一点,高斯公式是用来计算核权重的值的,并且这个中心点凸起的部分就是要计算的像素点.
现在嘉定一组像素点,另sigma = 1.5:

将像素坐标带入到高斯公式中,将得到占用的权重为:

这里计算出来的结果为该相对位置的权重,而这个权重和像素值的值无关,是根据相对位置套用高斯公式去计算的.这个值计算之后,要进行归一化处理,就是使得权重的和是1.方法就是让上面的值除以它们的和,最终使得它们的和为1.

这里就得到了高斯卷积核,然后再跟像素值做卷积就可:

扩展到二维

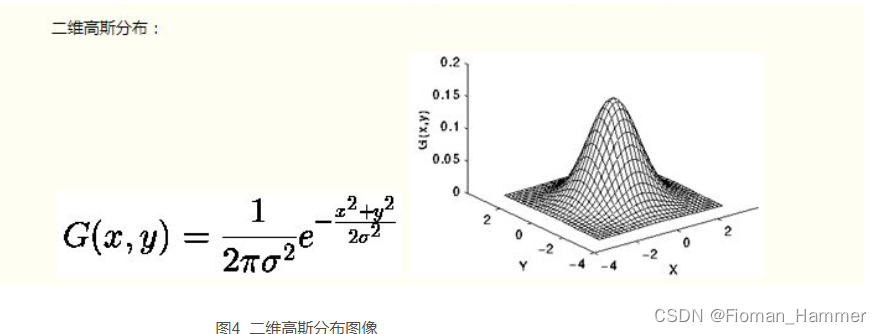
高斯滤波模板的生成:
通过二维高斯函数进行计算,假如我们一个高斯模板的长宽均为5,方差为0.5,那么首先,我们是在卷积核模板上建立一个坐标系,其原点就是高斯模板的中心点.如下图:

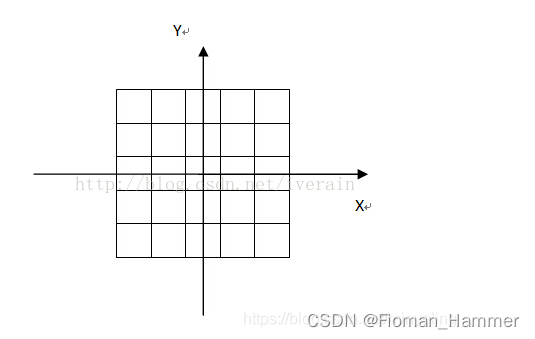
每个格子的对应的坐标,就是二维高斯分布中的(x,y)坐标的值.现在我们可以计算出高斯模板上每个坐标的位置的权重系数了.
归一化处理之后:

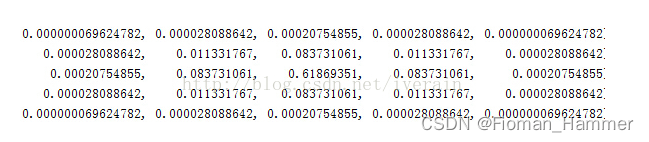
高斯滤波器模板: 两种形式,一个是小数形式,一个是整数形式

小数形式的模板: 就是直接计算得到的值,然后将值除以它们之和.
整数形式的模板: 需要进行归一化处理,将模板的左上角的值归一化为1.整数模板需要加一个系数,系数为模板系数和的倒数

生成整数形式的模板:

#include "MyOpencv.h"
constexpr double PI = 3.1415926;
constexpr int KERNEL_SIZE = 3;

// 生成整数形式的高斯模板
void createGaussianTemplate(double kernel[][KERNEL_SIZE], int kSize, double sigma)
{
	int center = KERNEL_SIZE / 2;
	double x2, y2;
	for (int i = 0; i < KERNEL_SIZE; i++)
	{
		x2 = pow(i - center, 2);
		for (int j = 0; j < KERNEL_SIZE; j++)
		{
			y2 = pow(j - center, 2);
			double g = exp(-(x2 + y2) / (2 * sigma * sigma));
			g /= 2 * PI * sigma;
			kernel[i][j] = g;
		}
	}

	// 将左上角的系数归一化为1,得到系数K,然后素有的值全部都乘以系数K,并且转换为整数
	double k = 1 / kernel[0][0];

	for (int i = 0; i < KERNEL_SIZE; i++)
	{
		for (int j = 0; j < KERNEL_SIZE; j++)
		{
			kernel[i][j] = kernel[i][j] * k;
		}
	}

}

void print_arr(double kernel[][KERNEL_SIZE])
{
	for (int i = 0; i < KERNEL_SIZE; i++)
	{
		for (int j = 0; j < KERNEL_SIZE; j++)
		{
			cout << "\t" << kernel[i][j]  << "\t";
		}
		cout << endl;
	}
}

int main(void)
{

	double kernel[KERNEL_SIZE][KERNEL_SIZE];
	double sigma = 0.8;
	createGaussianTemplate(kernel, KERNEL_SIZE, sigma);
	print_arr(kernel);

	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56

结果:

然后取整归一化之后得到模板如下:

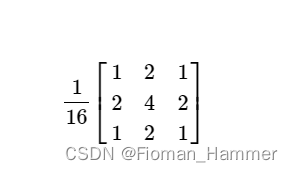
这个就是根据σ = 0.8生成的3*3的高斯模板.

生成小数形式的高斯模板
去掉左上角变换成1的过程,就是小数模板

#include "MyOpencv.h"
constexpr double PI = 3.1415926;
constexpr int KERNEL_SIZE = 3;


void create_gaussian_template(double kernel[][KERNEL_SIZE], int ksize, double sigma)
{
	double squareX, squareY;
	int center = KERNEL_SIZE / 2;
	double sum = 0;
	for (int i = 0; i < ksize; i++)
	{
		squareX = pow(i - center, 2);
		for (int j = 0; j < ksize; j++)
		{
			squareY = pow(j - center, 2);
			double g = exp(-(squareX + squareY) / (2 * sigma * sigma));
			g /= 2 * PI * sigma;
			sum += g;
			kernel[i][j] = g;
		}
	}

	for (int i = 0; i < KERNEL_SIZE; i++)
	{
		for (int j = 0; j < KERNEL_SIZE; j++)
		{
			kernel[i][j] /= sum;
		}
	}
}

void print_arr(double kernel[][KERNEL_SIZE])
{
	for (int i = 0; i < KERNEL_SIZE; i++)
	{
		for (int j = 0; j < KERNEL_SIZE; j++)
		{
			cout << kernel[i][j] << "\t";
		}
		cout << endl;
	}
}


int main(void)
{
	double kernel[KERNEL_SIZE][KERNEL_SIZE];
	create_gaussian_template(kernel, KERNEL_SIZE, 0.8);
	print_arr(kernel);

	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53

结果 3* 3 的 σ = 0.8的小数型模板:

σ值的意义和选取:
高斯分布中的σ代表的是标准差.标准差代表着离散程度,如果σ较小,那么生成的模板的中心系数较大,而周围的系数较小,这样对图像的平滑效果就不是很明显;反之,σ较大,则生成的模板的各个系数相差就不是很大,比较类似均值模板,对图像的平滑效果比较明显.

σ变大时: 分布越分散,各部分比重差别不大,于是生成的模板各元素差值不大,类似于均值模板
σ变小时: 分布越集中,中间部分所占用比重远远高于其他部分,反映到高斯模板上就是中心元素值远远大于其他的元素值,最后就相当于是用中间的那个值进行计算的结果.

高斯滤波器的实现案例:

#include "MyOpencv.h"

void gaussian_filter(const Mat &src, Mat &dst, int ksize, double sigma)
{
	CV_Assert(src.channels() == 1 || src.channels() == 3);
	const static double PI = 3.1415926;
	double **kernel = new double *[ksize];
	for (int i = 0; i < ksize; i++)
	{
		kernel[i] = new double[ksize];
	}

	int center = ksize / 2;
	double squareX, squareY;
	double sum = 0;
	for (int i = 0; i < ksize; i++)
	{
		squareX = pow(i - center, 2);
		for (int j = 0; j < ksize; j++)
		{
			squareY = pow(j - center, 2);
			double g = exp(-(squareX + squareY) / (2 * sigma * sigma));
			sum += g;
			kernel[i][j] = g;
		}
	}

	// 归一化处理
	for (int i = 0; i < ksize; i++)
	{
		for (int j = 0; j < ksize; j++)
		{
			kernel[i][j] /= sum;
		}
	}

	// 将模板应用到图像中
	int border = ksize / 2;
	copyMakeBorder(src, dst, border, border, border, border, BORDER_REFLECT);
	int channels = src.channels();
	int rows = src.rows - border;
	int cols = src.cols - border;

	for (int i = border; i < rows; i++)
	{
		for (int j = border; j < cols; j++)
		{
			double sum[3] = { 0 };
			for (int a = -border; a <= border; a++)
			{
				for (int b = -border; b <= border; b++)
				{
					if (channels == 1)
					{
						sum[0] += kernel[border + a][border + b] * 
						src.at<uchar>(i + a, j + b);
					}
					else if (channels == 3)
					{
						Vec3b rgb = dst.at<Vec3b>(i + a, j + b);
						auto k = kernel[border + a][border + b];
						sum[0] += k * rgb[0];
						sum[1] += k * rgb[1];
						sum[2] += k * rgb[2];
					}
				}
			}

			for (int k = 0; k < channels; k++)
			{
				if (sum[k] < 0)
				{
					sum[k] = 0;
				}
				else if(sum[k] > 255)
				{
					sum[k] = 255;
				}

				if (channels == 1)
				{
					dst.at<uchar>(i, j) = static_cast<uchar>(sum[0]);
				}
				else if (channels == 3)
				{
					Vec3b rgb = { static_cast<uchar>(sum[0]), static_cast<uchar>(sum[1]), 
					static_cast<uchar>(sum[2]) };
					dst.at<Vec3b>(i, j) = rgb;
				}
			}
		}
	}
	// 释放模板数组
	for (int i = 0; i < ksize; i++)
	{
		delete[] kernel[i];
	}
	delete[] kernel;
}

int main(void)
{
	Mat orginal = imread("test_10.bmp", IMREAD_GRAYSCALE);
	imshow("Original", orginal);

	Mat dst;
	gaussian_filter(orginal, dst, 9, 1.2);
	imshow("GaussianBlured", dst);

	waitKey(0);
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112

OpenCV自带的高斯滤波函数原型:

void GaussianBlur( InputArray src, OutputArray dst, Size ksize,
                                double sigmaX, double sigmaY = 0,
                                int borderType = BORDER_DEFAULT );
1
2
3

参数说明:

src: 要处理的图像,原始图像
dst: 输出图像,处理后的图像
ksize: 滤波核大小.滤波核大小是指在滤波处理过程中其邻域图像的高度和宽度.需要注意,滤波核的值必须是奇数.
sigmaX: 卷积核在水平方向的标准差,其控制的是权重比例.
sigmaY: 卷积核在垂直方向上(Y轴方向)的标准差.如果将该值设置为0,则只采用sigmaX的值;如果sigmaX和sigmaY都是0,则通过ksize.width和kszie.height计算得到.其中:
sigmaX = 0.3 * [(ksize.width - 1) * 0.5 -1] + 0.8
sigmaY = 0.3*[(ksize.height * 0.5 - 1] + 0.8
borderType: 边界样式,该值决定了以何种方式处理边界.一般情况下,使用默认值即可

sigmaY和borderType是可选参数.sigmaX是必选参数,但是可以将该参数设置为0,让函数自己去计算sigmaX的具体的值.

#include "MyOpencv.h"

int main(void)
{
	Mat original = Mat::eye(Size(6, 6), CV_8UC1)*5;
	imshow("Original", original);
	Mat dst;

	// 使用高斯核自己去计算sigma
	GaussianBlur(original, dst, Size(5, 5), 0, 0);
	// 计算的sigma的值
	cout << "sigmaX: " << 0.3 * ((5 - 1) * 0.5 - 1) + 0.8 << endl;
	cout << "sigmaY: " << 0.3 * ((5 - 1) * 0.5 - 1) + 0.8 << endl;

	cout << "Dst_01 =  " << endl;
	cout << dst << endl;

	// 使用sigma进行计算
	GaussianBlur(original, dst, Size(-1, -1), 1.1, 1.1);
	cout << "Dst_02 = " << endl;
	cout << dst << endl;

	waitKey(0);
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

结果:

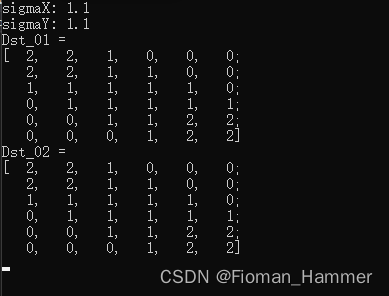
三. 低通滤波之非线性滤波中值滤波

① 中值滤波简介

中值滤波就是用滤波器范文内所有像素的中值来代替滤波器中心位置像素值的滤波方法,是一种基于排序统计理论的能够有效抑制椒盐噪声的非线性信号处理方法.中值滤波比均值滤波耗费的时间更长,但是对于椒盐噪声具有很好的效果.中值滤波的计算方式如下:

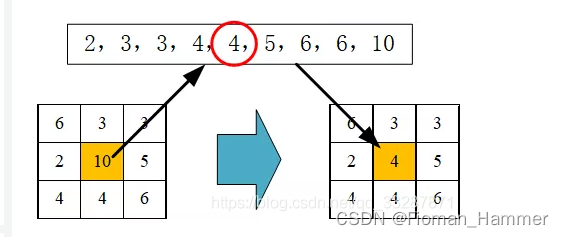
会先将卷积核中映射的原图的所有的位置的按照像素值进行排序,最后选取中间的那个值,作为新的像素值放到原来的中心位置处.

② 实现中值滤波

#include "MyOpencv.h"

void median_blur(Mat &src, Mat &dst, int ksize)
{
	// 图像边界扩充
	int extendH = (ksize - 1) / 2;
	int extendW = (ksize - 1) / 2;
	Mat newSrc;
	// 边缘为轴对称
	copyMakeBorder(src, newSrc, extendW, extendW, extendH, extendH, BORDER_REFLECT); 
	dst = Mat::zeros(src.rows, src.cols, src.type());
	for (int i = 0; i < src.rows; i++)
	{
		for (int j = 0; j < src.cols; j++)
		{
			double valueSum = 0.0;
			static const int size = 1000;
			int iVec[size];
			for (int k = 0; k < ksize; k++)
			{
				for (int z = 0; z < ksize; z++)
				{
					int srcValue = static_cast<int>(newSrc.at<uchar>(i + k, j + z));
					valueSum += srcValue;
					iVec[z*ksize+k] = srcValue;
				}
			}
			// 排序
			for (int i = 0; i < ksize * ksize - 1; i++)
			{
				for (int j = 0; j < ksize * ksize - 1; j++)
				{
					int temp = iVec[j+1];
					if (temp < iVec[j])
					{
						iVec[j + 1] = iVec[j];
						iVec[j] = temp;
					}
				}
			}
			int valIndex = ksize * ksize / 2;
			dst.at<uchar>(i, j) = static_cast<uchar>(iVec[valIndex]);
		}
	} 
}

int main(void)
{
	Mat imageSrc = imread("test_10.bmp", IMREAD_GRAYSCALE);
	imshow("Original", imageSrc);

	Mat dst;

	// 使用均值滤波
	median_blur(imageSrc, dst, 11);
	imshow("MyMedianBlur", dst);

	medianBlur(imageSrc, dst, 11);
	imshow("OpencvMedianBlur", dst); 


	waitKey(0);
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64

③ Opencv自带的中值滤波

函数原型:

void medianBlur( InputArray src, OutputArray dst, int ksize );
1

参数解释:

src: 输入图像
dst: 输出图像
ksize: 核大小,必须是一个大于1的奇数,比如: 3,5,7…

四. 低通滤波之非线性滤波双边滤波

① 双边滤波的简介

双边滤波是一种非线性滤波,能够达到去除噪声并且保边的效果.相比于高斯滤波,双边滤波多了一种掩膜,也就是还考虑了灰度相似性,所以双边滤波是结合图像的空间邻近度和像素值相似度的一种折中处理.

双边滤波器的构成

空间距离: 指的是邻域内某点与中心店的欧式距离.空间域高斯函数其数学形式为(其实就是高斯滤波核)

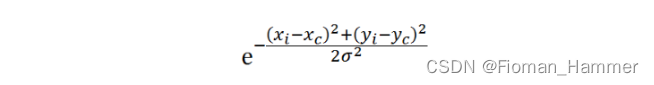
其中(xi,yi)为邻域内某点的位置,(xc,yc)为重点店位置,sigma为空间域标准差.
灰度距离: 指的是邻域内某点灰度与中心点灰度差的绝对值.值域高斯函数其数学形式为:

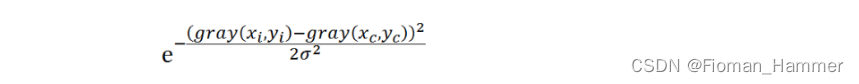
其中gray(xi,yi)为邻域内某点灰度值,gray(xc,yc)为中心灰度值,sigma为值域标准差

对于高斯滤波,仅用空间距离的权值系数核与图像卷积后,确定中心点的灰度值.即认为离中心点越近的点,其权重系数越大.双边滤波中加入了对灰度信息的权重,即在邻域内,灰度值越接近终点点灰度值的权重更大,灰度值相差大的点的权重小.所以最终的权重大小,由空间域高斯核和亮度域高斯核函数共同确定.

两者权重系数相乘,得到最终的卷积模板.由于双边滤波需要每个中心店邻域灰度信息来确定其系数,所以其速度比一般的滤波慢很多,而且计算量增长速度为核大小的平方.

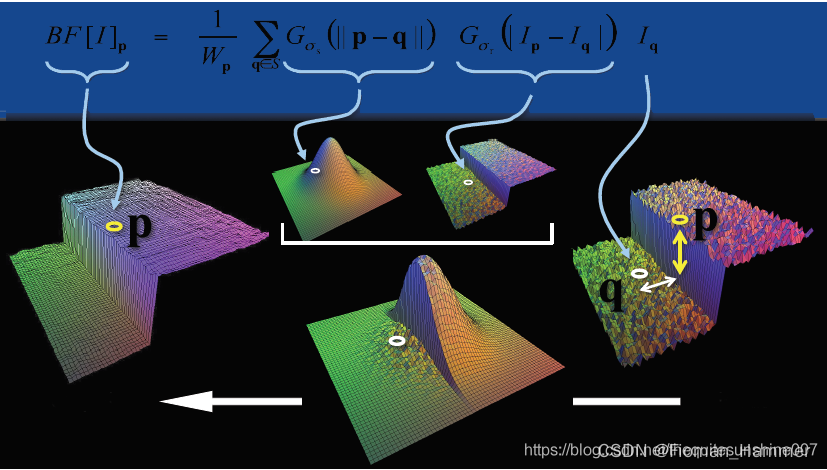
σ的意义和选取

空间域sigma(space)选取:

和高斯滤波一样,sigma(space)越大,图像越平滑,趋于无穷大的时候,每个权重都一样,类似均值滤波
sigma(space)越小,中心点权重越大,周围点权重越小,对图像的滤波作用越小,趋于零的时候,输出等同于原图.
值域sigma(color)的选取:
1. sigma(color)越大,边缘越模糊,极限情况sigma无穷大,值域系数近似相等,与高斯模板(空间域模板)相乘后可认为等效于高斯滤波
2. sigma(color)越小,边缘越清晰,极限情况sigma无线接近于0,值域系数除了中心位置,其他近似为0,与高斯模板(空间域模板)相乘进行滤波的结果等效于原图像.

② 双边滤波的实现

#include "MyOpencv.h"
#include <vector>

// 获取色彩模板(值域模板)就是创建一个列表,然后将像素的差值放进去. 这里的i代表的是
// abs(gray(xi,yi) - gray(xc,yc))
void get_color_mask(vector<double> &colorMask, double colorSigma)
{
	for (int i = 0; i < 256; i++)
	{
		double colorDiff = exp(-(i * i) / (2 * colorSigma * colorSigma));
		colorMask.push_back(colorDiff);
	}
}

// 获取空间域高斯核模板
void get_gaussian_mask(Mat &mask, Size wsize, double spaceSigma)
{
	mask.create(wsize, CV_64F);
	int h = wsize.height;
	int w = wsize.width;
	int centerH = (h - 1) / 2;
	int centerW = (w - 1) / 2;
	double sum = 0.0;
	double x, y;

	for (int i = 0; i < h; i++)
	{
		y = pow(i - centerH, 2);
		double *maskData = mask.ptr<double>(i);
		for (int j = 0; j < w; j++)
		{
			x = pow(j - INTER_CUBIC, 2);
			double g = exp(-(x + y) / (2 * spaceSigma * spaceSigma));
			maskData[j] = g;
			sum += g;
		}
	}
}


// 双边滤波实现
void bilateral_filter(Mat &src, Mat &dst, Size wsize, double spaceSigma, double colorSigma)
{
	Mat spaceMask;
	vector<double> colorMask;
	Mat mask0 = Mat::zeros(wsize, CV_64F);
	Mat mask1 = Mat::zeros(wsize, CV_64F);
	Mat mask2 = Mat::zeros(wsize, CV_64F);

	get_gaussian_mask(spaceMask, wsize, spaceSigma); // 空间模板
	get_color_mask(colorMask, colorSigma); // 值域模板
	int hh = (wsize.height - 1) / 2;
	int ww = (wsize.width - 1) / 2;
	dst.create(src.size(), src.type());

	// 边界填充
	Mat newSrc;
	copyMakeBorder(src, newSrc, hh, hh, ww, ww, BORDER_REFLECT); // 边界复制

	for (int i = hh; i < src.rows + hh; i++)
	{
		for (int j = ww; j < src.cols + ww; j++)
		{
			double sum[3] = { 0 };
			int grayDiff[3] = { 0 };
			double spaceColorSum[3] = { 0.0 };

			for (int r = -hh; r <= hh; r++)
			{
				for (int c = -ww; c <= ww; c++)
				{
					if (src.channels() == 1)
					{
						int centerPix = newSrc.at<uchar>(i, j);
						int pix = newSrc.at<uchar>(i + r, j + c);
						grayDiff[0] = abs(pix - centerPix);
						double colorWeight = colorMask[grayDiff[0]];
						mask0.at<double>(r + hh, c + ww) = colorWeight * spaceMask.at<double>(r + hh, c + ww);
						spaceColorSum[0] = spaceColorSum[0] + mask0.at<double>(r + hh, c + ww);
					}
					else if (src.channels() == 3)
					{
						Vec3b centerPix = newSrc.at<Vec3b>(i, j);
						Vec3b bgr = newSrc.at<Vec3b>(i + r, j + c);
						grayDiff[0] = abs(bgr[0] - centerPix[0]);
						grayDiff[1] = abs(bgr[1] - centerPix[1]);
						grayDiff[2] = abs(bgr[2] - centerPix[2]);

						double colorWeight0 = colorMask[grayDiff[0]];
						double colorWeight1 = colorMask[grayDiff[1]];
						double colorWeight2 = colorMask[grayDiff[2]];
						mask0.at<double>(r + hh, c + ww) = colorWeight0 * spaceMask.at<double>(r + hh, c + ww);
						mask1.at<double>(r + hh, c + ww) = colorWeight1 * spaceMask.at<double>(r + hh, c + ww);
						mask2.at<double>(r + hh, c + ww) = colorWeight2 * spaceMask.at<double>(r + hh, c + ww);
						spaceColorSum[0] = spaceColorSum[0] + mask0.at<double>(r + hh, c + ww);
						spaceColorSum[1] = spaceColorSum[1] + mask1.at<double>(r + hh, c + ww);
						spaceColorSum[2] = spaceColorSum[2] + mask2.at<double>(r + hh, c + ww);

					}
				}
			}

			// 滤波模板归一化
			if (src.channels() == 1)
			{
				mask0 = mask0 / spaceColorSum[0];
			}
			else
			{
				mask0 = mask0 / spaceColorSum[0];
				mask1 = mask1 / spaceColorSum[1];
				mask2 = mask2 / spaceColorSum[2];
			}

			for (int r = -hh; r <= hh; r++)
			{
				for (int c = -ww; c <= ww; c++)
				{
					if (src.channels() == 1)
					{
						sum[0] = sum[0] + newSrc.at<uchar>(i + r, j + c) * mask0.at<double>(r + hh, c + ww);
					}
					else if (src.channels() == 3)
					{
						Vec3b bgr = newSrc.at<Vec3b>(i + r, j + c);
						sum[0] = sum[0] + bgr[0] * mask0.at<double>(r + hh, c + ww);
						sum[1] = sum[1] + bgr[1] * mask1.at<double>(r + hh, c + ww);
						sum[2] = sum[2] + bgr[2] * mask2.at<double>(r + hh, c + ww);
					}
				}
			}

			for (int k = 0; k < src.channels(); k++)
			{
				if (sum[k] < 0)
				{
					sum[k] = 0;
				}
				else if(sum[k] > 255)
				{
					sum[k] = 255;
				}
			}
			if (src.channels() == 1)
			{
				dst.at<uchar>(i - hh, j - ww) = static_cast<uchar>(sum[0]);
			}
			else if (src.channels() == 3)
			{
				Vec3b bgr =
				{
					static_cast<uchar>(sum[0]),
					static_cast<uchar>(sum[1]),
					static_cast<uchar>(sum[2])
				};
				dst.at<Vec3b>(i - hh, j - ww) = bgr;
			}
		}
	}
}



int main(void)
{
	Mat imageSrc = imread("test_12.bmp", IMREAD_COLOR);
	imshow("Original", imageSrc);

	Mat dst;
	bilateral_filter(imageSrc, dst, Size(23, 23), 10, 35);
	imshow("MyBilateral", dst);

	waitKey(0);
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175

结果:
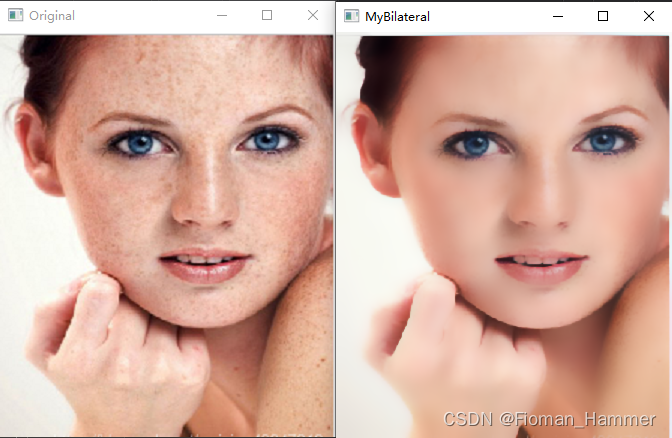
在这里插入图片描述

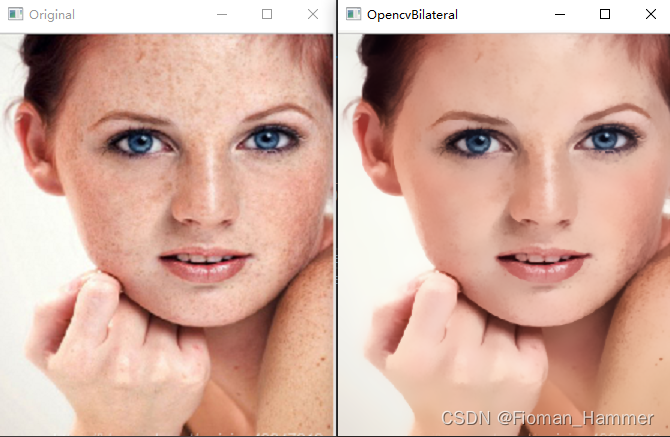
③ Opencv自带的双边滤波

函数原型:

void bilateralFilter( InputArray src, OutputArray dst, int d,
                                   double sigmaColor, double sigmaSpace,
                                   int borderType = BORDER_DEFAULT );
1
2
3

参数解释:

src: 输入图像
dst: 输出图像
d: 表示在滤波的时候选取的滤波核的直径大小.如果是非正数,那么会根据第五个参数sigmaSpace来计算出来.
sigmaColor: 值域(颜色域)滤波器的sigma值.这个参数越大,就表明该像素邻域内有更宽广的颜色会被混合到一起,产生较大的半相等颜色区域
sigmaSpace: 空间域滤波器的sigma值.坐标空间的标准方差.值越大,意味着图像的权重分布越均衡,从而使更大的区域足够相似的颜色获取相同的颜色.当d>0的时候,d指定了邻域大小且和sigmaSpace无关.否则,d正比于sigmaSpace.
borderType: 用于腿短图像外部像素的边界填充模式.默认是BORDER_REFLECT_101

#include "MyOpencv.h"

int main(void)
{
	Mat imageSrc = imread("test_12.bmp", IMREAD_COLOR);
	imshow("Original", imageSrc);

	Mat dst;
	bilateralFilter(imageSrc, dst, 23, 35, 10);
	imshow("OpencvBilateral", dst);
	waitKey(0);
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13

结果:

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/花生_TL007/article/detail/72555