图论：并查集求最小环

图论：并查集求最小环

概念：

图、路、环：

一个有向图由G=(N,A)表示，其中N表示节点集，A表示边集边(i,j)为一有序对，i为出发节点，j为终止节点。在无向图中(i,j)与(j,i)一致。

路是由节点及其对应的边依次相连构成。

环是出发节点和终止节点相同的路。

如果一条路不含重复边和重复节点，就被称做简单路，出发节点和终止节点相同的简单路就被称为简单环。

对于有向图而言 可以使用拓扑排序的方式找出图中的环

引入例题：

P2661 信息传递

题目描述

有 nnn 个同学（编号为 111 到 nnn ）正在玩一个信息传递的游戏。在游戏里每人都有一个固定的信息传递对象，其中，编号为 iii 的同学的信息传递对象是编号为 TiT_iTi 的同学。

游戏开始时，每人都只知道自己的生日。之后每一轮中，所有人会同时将自己当前所知的生日信息告诉各自的信息传递对象（注意：可能有人可以从若干人那里获取信息， 但是每人只会把信息告诉一个人，即自己的信息传递对象）。当有人从别人口中得知自 己的生日时，游戏结束。请问该游戏一共可以进行几轮？

输入格式

共2行。

第1行包含1个正整数 n ，表示 n 个人。

第2行包含 n 个用空格隔开的正整数 T1,T2,⋯⋯ ,Tn，其中第 iii 个整数 Ti 表示编号为 i 的同学的信息传递对象是编号为 Ti 的同学， Ti≤n 且 Ti≠i。

输出格式

1个整数，表示游戏一共可以进行多少轮。

输入输出样例

输入 #1

5
2 4 2 3 1
1
2

输出 #1

3
1

说明/提示

样例1解释

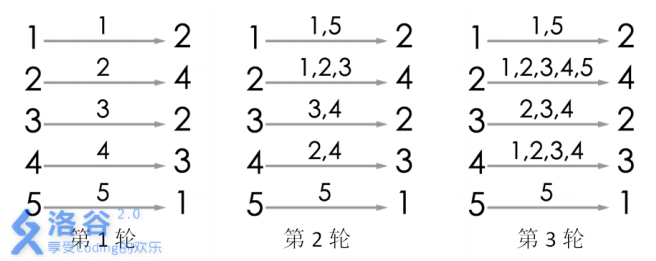
游戏的流程如图所示。当进行完第3 轮游戏后， 4号玩家会听到 2 号玩家告诉他自己的生日，所以答案为 3。当然，第 3轮游戏后，2号玩家、3 号玩家都能从自己的消息来源得知自己的生日，同样符合游戏结束的条件。

对于 30%的数据， n≤200；

对于 60%的数据， n≤2500；

对于100%的数据， n≤200000。

解析：

首先，通过题目可能想到的是暴力建立set判重。

本题难点在于，怎么看出他是一并查集的题，讲真，题目的描述，一轮一轮的感觉与并查集风牛马牛不相及，但是非要联系的话，首先想到是：图，那把图画出来：

画完我们得知，要求的游戏轮数，就抽象在这个环里，简言之就是：存在环的话，生日就可以传到自己耳朵里，传递次数为环的大小。

来源题解：

anyway

把每个同学看成一个点，信息的传递就是在他们之间连有向边，游戏轮数就是求最小环。

图论求最小环，我在里面看到了并查集。

假如说信息由A传递给B，那么就连一条由A指向B的边，同时更新A的父节点**，A到它的父节点的路径长也就是B到它的父节点的路径长+1。**

这样我们就建立好了一个图，之后信息传递的所有环节都按照这些路径。游戏结束的轮数，也就是这个图里最小环的长度。

如果有两个点祖先节点相同，那么就可以构成一个环，长度为两个点到祖先节点长度之和+1。

和下面的并查集有点不一样的。

代码：

（简略注释在代码中给出，*下方有详细解释）

import java.util.Scanner;
/*
 * P2661 信息传递     并查集求最小环
 */
public class P2661 {
	static Scanner sc= new Scanner(System.in);
	static int n=sc.nextInt();
	static int f[]=new int[200005];//这是节点的父节点数组
	static int d[]=new int[200005];//这是到父节点的距离
	static int min=n;//设置一个最小环数（初始值设为最大）
	public static void main(String[] args) {
		for (int i = 1; i <= n; i++) {
			f[i]=i;//初始化，让自己当自己的”嗲“；
		}
		for (int i = 1; i <=n ; i++) {
			int to=sc.nextInt();
			check(i,to);//------------------------------------*1*
		}
		System.out.println(min);
	}

	private static void check(int i, int to) {
		// 经典check函数
		int x=getfa(i);
		int y=getfa(to);//找爹，也就是“让boss之间谈话”
		if(x!=y){
			f[x]=y;//让boss会话，并认右为王
			d[i]=d[to]+1;//-----------------------------------*2*
		}else{
			min=Math.min(min, d[i]+d[to]+1);//----------------*3*
            //长度为两个点到祖先节点长度之和+1。
		}
	}

	private static int getfa(int x) {
        //经典找爹函数
		if(f[x]!=x){
			int origin=f[x];
			
			f[x]=getfa(f[x]);//小细节：不是getfa(x)是getfa(f[x]);
			d[x]+=d[origin];//-------------------------------*4*
            //更新路径长（原来连在父节点上）。
		}	
		return f[x];
	}
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

难点&精彩点：

1. 首先就是并查集的知识：建议先学几个并查集的例子在做这个题，否则不懂，强推《啊哈！算法》p200页的知识，记住“擒贼先擒王的口诀”和“以左为王”的口诀

2. *1*这里我认为理解起来有难度，（呵呵，也许是我太笨，反正就这个循环，我受题面“轮数”影响，想了好久才想出来）这里其实和题目的轮数无关，以后也不要记轮数了，总之就是要把这几个点一个个输入，边输入边判断已有的点集合，是否存在环，以及是否存在最小值。

3. *2*这里的d[i]=d[to]+1;要点有二，一是方括号里必须是判断值，而不是其父值。也就是说”找祖宗“只是为了判断是否在一点集内，而对父节点的距离数组进行记录时是对i,to,操作的。而加一操作见下图：

4. *3*,这个地方，，怎么说，代码作者很强，应该是分析出的规律：长度为两个点到祖先节点长度之和+1。

5. *4*这地方，的确很难想，这个地方和路径压缩有关，很巧妙，我试了试，只能把他放在递归后侧回溯的过程中，然后相当于“拾级而上，不断累加”太难想了对我···哈哈感觉遇到了瓶颈。（菜鸡的瓶颈未免也太低啦哈哈）

小结：

很好的考察了并查集，递归，图论的部分知识。尤其是在两个经典并查集函数中，其中关于路径的记录很考察人的水平。

，这个地方和路径压缩有关，很巧妙，我试了试，只能把他放在递归后侧回溯的过程中，然后相当于“拾级而上，不断累加”太难想了对我···哈哈感觉遇到了瓶颈。（菜鸡的瓶颈未免也太低啦哈哈）

小结：

很好的考察了并查集，递归，图论的部分知识。尤其是在两个经典并查集函数中，其中关于路径的记录很考察人的水平。