上采样、下采样以及Pytorch中的卷积与反卷积(转置卷积)方法介绍(conv2d和convTranspose2d)_convtranspose2d进行2倍上采样

1. 上采样与下采样

1.1 上采样

上采样（upsampling），又叫放大图像、图像插值(interpolating)，主要目的是放大原图像，从而可以显示在更高分辨率的显示设备上。上采样有3种常见的方法：双线性插值(bilinear)，反卷积(Transposed Convolution)，反池化(Unpooling)。

• 插值法：最近邻算法、双线性插值算法、双三次插值算法（bicubic）
• 反卷积：又称为转置卷积
• 反池化：平均池化的反池化是把池化后的平均数字结果分布到池化前图像上的每个像素格子上。 最大池化的反池化是把池化后的最大数字结果填充到池化前图像上对应的像素格子上，而其他格子则填充0。

1.2 下采样

下采样（subsampled）或降采样（downsampled）或者称为缩小图像，它的主要目的有两个：1、使得图像符合显示区域的大小；2、生成对应图像的缩略图。

下采样一般为池化操作。池化最直观的作用便是降维，常见的池化有最大池化、平均池化和随机池化；池化层不需要训练参数。

2. 卷积函数——Conv2d

2.1 卷积函数说明

卷积操作可以压缩整合图片特征，让[通道, 宽, 高]分别为$[c,h,w]$的特征图片通过Conv2d。变为更多的通道(维度)$c$，更小的尺寸$[h,w]$。也就是说，当输入为一组图片$[n,c,h,w]$格式时，输出也为$[n,c,h,w]$格式。

卷积函数Conv2d定义形式如下所示。

torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, 
groups=1, bias=True, padding_mode='zeros', device=None, dtype=None)
1
2

卷积函数参数说明：

• in_channels (int) – 输入信号通道数(channels)；
• out_channels (int) – 输出信号通道数(channels)；
• kernel_size (int or tuple) – 卷积核的大小；卷积核尺寸，尺寸越大‘感受野’越大，及处理的特征单位越大，同时计算量也越大
• stride (int or tuple, optional) – 卷积步长(默认为1)；卷积核移动的步数，默认1步，增大步数会忽略局部细节计算，适用于高分辨率的计算提升
• padding (int, tuple or str, optional) – 输入信号四周的填充，默认填充0。就是填充的意思，通过padding，可以填充图片的边缘，让图片的边缘的特征得到更充分的计算(不至于被截断)
• padding_mode (string, optional) – ‘zeros’, ‘reflect’, ‘replicate’ or ‘circular’. Default: ‘zeros’；
• dilation (int or tuple, optional) – 卷积核元素之间的间距，默认为1，也就是常规的卷积方式；
• groups (int, optional) – 从输入通道到输出通道的阻塞连接数，默认为1；
• bias (bool, optional) – 如果bias=True，添加偏置，默认为True；

卷积操作的输入与输出尺寸之间的关系如下所示。注意下列除法为 向下取正。简化版为：$H_o=(H_i+2p-d\ast (k-1)-1)/s+1$

2.2 卷积操作可视化与举例

（1）举例一：padding=0,stride=1,kernel_size=3

假设padding=0，stride=1，kernel_size=3。下图中，蓝色为输入[4,4]，蓝色上的阴影为卷积核[3,3]，绿色为输出[2,2]，蓝色边缘的白色框为padding。可视化效果如下。

代码表示形式如下：

import torch
import torch.nn as nn

x = torch.randn(1,1,4,4) # [n,c,h,w]
l = nn.Conv2d(1,1,3)#Conv2d(1, 1, kernel_size=(3, 3), stride=(1, 1),padding=0)
y = l(x)

print(y.shape) # torch.Size([1, 1, 2, 2])
1
2
3
4
5
6
7
8

（2）举例二：padding=2,stride=1,kernel_size=4

假设padding=2，stride=1，kernel_size=4。下图中，蓝色为输入[5,5]，蓝色上的阴影为卷积核[4,4]，绿色为输出[6,6]，蓝色边缘的白色框为padding[2,2]。可视化效果如下。

代码表示形式如下：

import torch
import torch.nn as nn

x = torch.randn(1,1,5,5) # [n,c,h,w]
l = nn.Conv2d(1,1,4,padding=2)#Conv2d(1, 1, kernel_size=4,stride=1,padding=2)
y = l(x)

print(y.shape) # torch.Size([1, 1, 6, 6])
1
2
3
4
5
6
7
8

3. 反卷积(转置卷积)——convTranspose2d

反卷积（Deconvolution）的概念第一次出现是Zeiler在2010年发表的论文Deconvolutional networks中，但是并没有指定反卷积这个名字，反卷积这个术语正式的使用是在其之后的工作中。

转置卷积，也称为反卷积(deconvlution)和分部卷积(fractionally-strided convolution)。为卷积的逆操作，即把特征的维度压缩，但尺寸放大。注意它 不是真正意义上 的卷积的逆操作。通过反卷积，只能恢复原矩阵的大小，但并不能完全恢复原矩阵的数值。

3.1 反卷积原理

所谓的反卷积，就是卷积的逆操作，反卷积就可以看成通过卷积核透视。如下图所示：

比如左上角的图，拿55举例，它的输出为[[55,110,55],[110,55,110],[55,55,110]]。我们将得到的四张特征图进行叠加（重合的地方其值相加），可以得到下图：

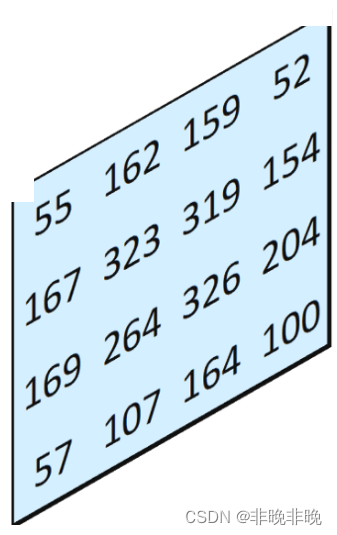
3.2 反卷积函数说明

该模块可视为Conv2d相对于其输入的梯度。卷积函数convTranspose2d定义形式如下所示。

torch.nn.ConvTranspose2d(in_channels, out_channels, kernel_size, stride=1, padding=0, output_padding=0, 
groups=1, bias=True, dilation=1, padding_mode='zeros', device=None, dtype=None)
1
2

反卷积参数说明如下，stride、padding和output_padding参数需要单独理解，其他大部分参数与卷积相似。

• in_channels(int) – 输入信号的通道数;
• out_channels(int) – 卷积产生的通道数;
• kerner_size(int or tuple) - 卷积核的大小;
• stride(int or tuple,optional) - 输入层之间的间隔，默认为1

stride=1时，输入层元素之间没有间隔，当stride=2时，输入层元素之间间隔为1，stride=3时，输入层元素之间间隔为2，以此类推。

• padding(int or tuple, optional) - 卷积核与输入层相交的最少像素参数，默认为0，也就是说最少要相交1个点;

padding=0时，卷积核和输入层相交一个像素，当padding=1时，卷积核和输入层相交2个像素，依此类推；

• output_padding(int or tuple, optional) - 输出数据每条边的填充0的个数，默认为0;

output_padding=0表示不进行填补，output_padding=1表示进行填补一圈0，等于2表示进行填补2圈0.

• dilation(int or tuple, optional) – 卷积核元素之间的间距
• groups(int, optional) – 从输入通道到输出通道的阻塞连接数
• bias(bool, optional) - 如果bias=True，添加偏置，默认为True

反卷积操作的输入与输出尺寸之间的关系如下所示。从公式可以看出，它是卷积的反求关系，简化版：$H_o=H_i\ast 2-2p+d\ast (k-1)+output\_padding+1$

$$H_{out}=(H_{in}-1)\times stride[0]-2\times padding[0]+dilation[0]\times (kernel\_size[0]-1)+output\_padding[0]+1$$
$$W_{out}=(W_{in}-1)\times stride[1]-2\times padding[1]+dilation[1]\times (kernel\_size[1]-1)+output\_padding[1]+1$$

3.3 反卷积操作可视化与举例

（1）举例一：padding=0,kernel_size=3,stride=1

padding = 0，表示蓝色的输入[2,2]与卷积核最少有(1,1)个像素相交，stride = 1，表示输入输入数据没有间隔。具体动态图视如下：

代码表示形式如下：

import torch
import torch.nn as nn

x = torch.randn(1,1,2,2)
l = nn.ConvTranspose2d(1,1,3)#Conv2d(1, 1, kernel_size=3,stride=1,padding=0)
y = l(x) 

print(y.shape) # torch.Size([1, 1, 4, 4])
1
2
3
4
5
6
7
8

（2）举例二：padding=2,kernel_size=4,stride=1

padding = 2表示蓝色输入数据[6,6]与卷积核函最少交(3,3)个像素，stride=1表示输入数据没有间隔。具体动态图视如下：

代码表示如下：

import torch
import torch.nn as nn

x = torch.randn(1,1,6,6)
l = nn.ConvTranspose2d(1,1,4,padding=2)#Conv2d(1, 1, kernel_size=4,stride=1,padding=2)
y = l(x)

print(y.shape) # torch.Size([1, 1, 5, 5])
1
2
3
4
5
6
7
8

（3）举例三：padding=2,kernel_size=3,stride=1

padding = 2表示蓝色输入数据[7,7]与卷积核函最少交(3,3)个像素，stride=1表示输入数据没有间隔。具体动态图视如下：

代码表示如下：

import torch
import torch.nn as nn

x = torch.randn(1,1,7,7)
l = nn.ConvTranspose2d(1,1,3,padding=2)#Conv2d(1, 1, kernel_size=3,stride=1,padding=2)
y = l(x) 

print(y.shape) # torch.Size([1, 1, 5, 5])
1
2
3
4
5
6
7
8

（4）举例4：padding=0,kernel_size=3,stride=2

padding = 0表示蓝色输入数据[2,2]与卷积核函最少交(1,1)个像素，stride=2表示输入数据间隔1个像素就填充0值。具体动态图视如下：

代码表示如下：

import torch
import torch.nn as nn

x = torch.randn(1,1,2,2)
l = nn.ConvTranspose2d(1,1,3,stride=2,padding=0)#Conv2d(1, 1, kernel_size=3,stride=2,padding=0)
y = l(x) 

print(y.shape) # torch.Size([1, 1, 5, 5])
1
2
3
4
5
6
7
8

---

Conv2d参考链接：https://pytorch.org/docs/stable/generated/torch.nn.Conv2d.html?highlight=conv2d#torch.nn.Conv2d
ConvTranspose2d参考链接：https://pytorch.org/docs/1.11/generated/torch.nn.ConvTranspose2d.html?highlight=convtranspose2d#torch.nn.ConvTranspose2d

反卷积网络论文：https://www.matthewzeiler.com/mattzeiler/deconvolutionalnetworks.pdf

卷积动态图：https://github.com/vdumoulin/conv_arithmetic