走廊泼水节

走廊泼水节

---

题目描述

---

核心思路

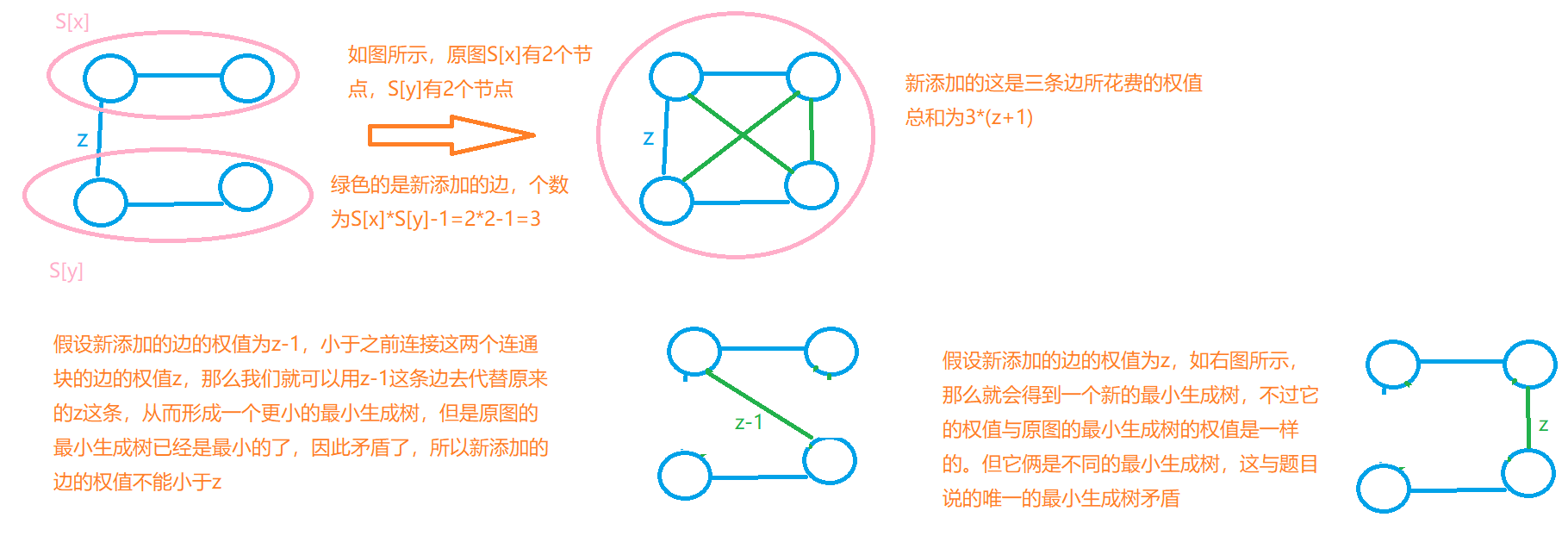
题目的意思是：现在有一张图，已知了这张图的最小生成树了，然后我们需要把这张图变成完全图（任意两个节点之间都有边相连），使得这张完全图中的最小生成树仍然与原图的最小生成树是同一颗。把原图变成完全图，就需要加边，题目想要我们求的是加的这些边的权值总和的最小值。

设当前扫描到边$(x,y)$，其权值为$z$，设$x$所在连通块为$S_x$，$y$所在连通块为$S_y$，此时应该合并$S_x$与$S_y$。合并后的$S_x\cup S_y$构成一棵树的结构。

$\forall u\in S_x$，$v\in S_y$，如果$(u,v)\ne (x,y)$，则在最终的完全图中，我们肯定需要在$(u,v)$之间增加一条边。于是，无向边$(u,v)$、$S_x$中从$u$到$x$的路径、无向边$(x,y)$、$S_y$中从$v$到$y$的路径，就形成了一个环，如下图所示：

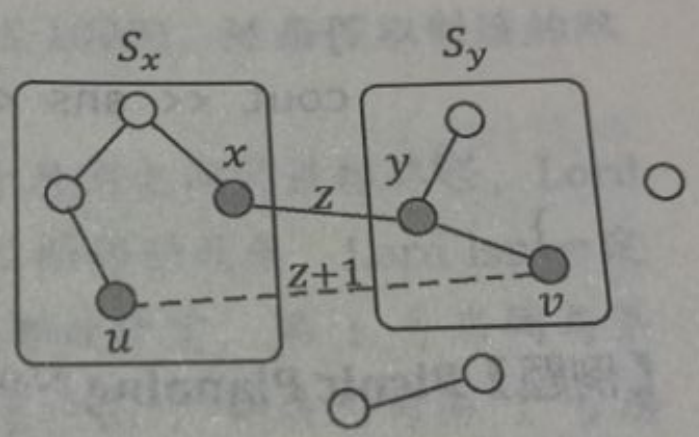
为了保证$(x,y)$一定在最小生成树中，就必须让$(x,y)$是连接集合$S_x$和集合$S_y$的权值最小的边（否则就可以用边$(u,v)$去代替边$(x,y)$形成一棵最小生成树了，这与已有的最小生成树有矛盾）。因此，为了保证所添加的这些边的权值总和最小，那么可以让所有新添加的这些边的权值都为$z+1$。

设集合$S_x$中有$|S_x|$个节点，集合$S_y$中有$|S_y|$个节点，由于完全图是任意两个节点之间都需要有边相连，因此总共需要$|S_x|\times |S_y|$条边，但是由于边$(x,y)$已经是原图中已有的一条连接$S_x$和$S_y$这两个连通块中的一条边了，因此应该从$|S_x|\times |S_y|$减去这条已有的连接边。也就是说，合并$S_x$和$S_y$这两个连通块，需要边数为$|S_x|\times |S_y|-1$，由于每条边的权值都为$z+1$。因此增加的边的权值总和最小是$(z+1)\times$$(|S_x|\times |S_y|-1)$

问题：为什么新添加的边权一定是$z+1$，而不能是$z$或者小于$z$呢？如何理解$(z+1)\times$$(|S_x|\times |S_y|-1)$这个式子呢？

如下图所示：可以发现，合并了两个连通块后，所形成的这个连通块就已经是完全图了，以此类推，合并完所有的连通块后，所得到的最终那个连通块就是完全图。

总结一下就是：

假设有两个连通块$A,B$，要扩展为完全图，那么就需要$A$中的每个节点都与$B$中的每个节点相连。对于一条最小生成树上的边$E$，可以看作$E$连接了$A$和$B$这两个连通块，那么要将$A$和$B$连接成一个完全图需要添加的边数就是$cnt[A]\times cnt[B]-1$，减去1就是减去已经存在的$E$这条边，其中$cnt[A]$表示连通块$A$中的节点数，$cnt[B]$表示连通块$B$中的节点数。设$E$的边权为$z$，由上图的可知，新增加的边权不可能$\le z$，必须是$>z$的。为了让增加的边权总和最小，则需要让新增加的边权为$z+1$就好了。

那么合并这两个连通块的花费就是$(z+1)\times (cnt[A]\times cnt[B]-1)$。设ans是答案，那么在每次合并连通块时，让$ans$累加上花费就好了。

还有一点，题目要求的是最小的完全图，因此采用贪心的策略：先把树上的边按权值从小到大排序，然后依次枚举即可。

---

代码

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=6010,M=N;
//n是点数  m是边数
int n,m;
struct Edge{
    int a,b,w;
    bool operator < (const Edge& W)const{
        return w<W.w;
    }
}edges[M];
int p[N];
int cnt[N];     //cnt[i]表示第i个连通块中点的数量
int find(int x)
{
    if(x!=p[x])
        p[x]=find(p[x]);
    return p[x];
}
int Kruskal()
{
    int res=0;  //增加的边的权值总和最小值
    sort(edges,edges+m);    //将边权从小到大排序
    for(int i=1;i<=n;i++)
    {
        p[i]=i;     //初始化并查集  每个点都是独立的连通块
        cnt[i]=1;   //由于每个点都是独立的连通块  所以每个连通块内只有1个节点
    }
    for(int i=0;i<m;i++)
    {
        int a=find(edges[i].a);
        int b=find(edges[i].b);
        int w=edges[i].w;
        if(a!=b)
        {
            //每次合并两个连通块都会产生(cnt[a]*cnt[b]-1)*(w+1)的开销
            //所以要让res累加这些开销
            res+=(cnt[a]*cnt[b]-1)*(w+1);
            //将a这个连通块中所有点的数量都累加到b这个连通块中
            cnt[b]+=cnt[a];
            //将集合a合并到集合b,现在a的祖宗节点是b
            p[a]=b;
        }
    }
    return res;
}
int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d",&n);
        //根据题目输入可以知道 有n个点 则有n-1条边
        m=n-1;
        //读入m条边的信息
        for(int i=0;i<m;i++)
        {
            int a,b,w;
            scanf("%d%d%d",&a,&b,&w);
            edges[i]={a,b,w};
        }
        int t=Kruskal();
        printf("%d\n",t);
    }
    return 0;
}   
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69

---