Codeforces Round 911 (Div. 2) --- D题题解_codeforces round 912 (div. 2)insert and equalize

D. Small GCD

Problem - D - Codeforces

题目大意：

给你一个数组，你可以在里面任选三个数ai aj ak，要求i j k 互不相同， 现定义一个函数f(a,b,c)=gcd(a,b)，其中a 和 b为a，b，c中较小的两个。求f(a,b,c)的累加和。更通常的说就是求

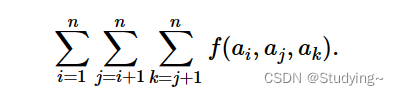
思路解析：

因为他是求任意三个数的函数值的累加和，所以我们ai aj ak的位置并不影响答案，那我们可以直接将整个数组排序，因为对于 ai aj定了之后 ak可以是任意的（ak > ai, ak > aj)，即k能选取的范围就是gcd(ai, aj)的次数。如果排序后 确定ai aj 后我们直接使gcd(ai, aj) * （n-j).

但是我们暴力枚举 ai 和 aj 的话，时间复杂度大概为 O(5*10^9),这个会被卡住，所以我们需要想到一个好的方法，又因为100000它的因子最多为128个，我们可以直接预处理，得到【1，100000】的每个数的所有因子，这样我们就把它的公因数控制住了，当公因数为t时，能贡献多少答案，但是公因数为t，它的最大公因数可能为t的倍数，所以这里需要使用容斥原理来做。

答案怎么统计？

for (int i = 0; i < n; i++) {
                for (int j = 0; j < 128; j++) {
                    if (num[arr[i]][j] == 0) break;
                    // (n - i - 1) k 可以枚举多少个
                    // num[arr[i]][j] 公因数
                    // nums[num[arr[i]][j]] 公因数的个数
                    f[num[arr[i]][j]] += (long) nums[num[arr[i]][j]] * (n - i - 1);
                    nums[num[arr[i]][j]]++;
                }
            }

之前的个数因数为t的数有nums[num[arr[i]][j]]个，所以对于当前这个b来说他的a有nums[num[arr[i]][j]]个选择，然后乘以c能选择的个数。

代码：

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.StreamTokenizer;
import java.util.Arrays;
 
/**
 * @ProjectName: study3
 * @FileName: Ex31
 * @author:HWJ
 * @Data: 2023/11/27 9:29
 */
public class Ex31 {
    static int[][] num = new int[100005][128];
 
    public static void main(String[] args) throws IOException {
 
        for (int i = 1; i <= 100000; i++) {
            int k = 0;
            for (int j = 1; j <= Math.sqrt(i); j++) {
                if (i % j == 0) {
                    num[i][k++] = j;
                    if (j != i / j) {
                        num[i][k++] = i / j;
                    }
                }
            }
        }
        StreamTokenizer in = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
        in.nextToken();
        int t = (int) in.nval;
        for (int o = 0; o < t; o++) {
            in.nextToken();
            int n = (int) in.nval;
            int[] arr = new int[n];
            int[] nums = new int[100005];
            long[] f = new long[100005];
            for (int i = 0; i < n; i++) {
                in.nextToken();
                arr[i] = (int) in.nval;
            }
            Arrays.sort(arr);
            long ans = 0;
            for (int i = 0; i < n; i++) {
                for (int j = 0; j < 128; j++) {
                    if (num[arr[i]][j] == 0) break;
                    // (n - i - 1) k 可以枚举多少个
                    // num[arr[i]][j] 公因数
                    // nums[num[arr[i]][j]] 公因数的个数
                    f[num[arr[i]][j]] += (long) nums[num[arr[i]][j]] * (n - i - 1);
                    nums[num[arr[i]][j]]++;
                }
            }
            for (int i = 100000; i >= 1; i--) {
                for (int j = i + i; j <= 100000; j+=i) {
                    f[i] -= f[j]; // 容斥处理
                }
            }
            for (int i = 100000; i >= 1; i--){
                ans += f[i] * i;
            }
            System.out.println(ans);
        }
    }
}