【排序算法系列之一】python实现十大排序算法_python快读排序

目录：

        冒泡排序(稳定性排序)

        快速排序(不稳定性排序)

        插入排序(稳定性排序)

        希尔排序(稳定性排序)

        选择排序(不稳定性排序)

---

前序：

由于涉及到两个数据位置的交换，所以首先定义了一个交换函数swap,利用两个数连续三次异或操作即可完成两数的交换；代码如下：

def swap(array,i,j):
    # 两个数连续三次异或操作后交换位置
    array[i] = array[i] ^ array[j]
    array[j] = array[i] ^ array[j]
    array[i] = array[i] ^ array[j]
    return array

一、冒泡排序

        冒泡排序是一种简单的排序算法，它也是一种稳定排序算法。其实现原理是重复扫描待排序序列，并比较每一对相邻的元素，元素数值大的往后移动。一直重复这个过程，直到没有任何两个相邻元素可以交换，就表明完成了排序。

该算法的最差时间复杂度为O(n^2)，最优时间复杂度为O(n)，平均时间复杂度为 O(n^2)。 

思路：比较相邻的元素。如果第一个比第二个大，就交换位置，一直比到最后两对。 n个数需要比较n-1次，最后一个数字不用比较。外循环决定循环次数，内循环比较每一个位置数的大小.

def BubbleSort(array):
    arr_len = len(array)
    # 外循环从第一位迭代至最后一位，最后一次不用比较
    for i in range(arr_len-1):
        # 内循环将第一位迭代比较至arr_len-i位，因为i位置后的是已经排好序的不用重复比较
        for j in range(arr_len-i):
            if (j + 1 == arr_len):
                break
            elif(array[j] > array[j+1]): 
                array = swap(array,j,j+1)
            else:
                continue
    return array

---

二、快速排序

        快速排序又是一种分而治之思想在排序算法上的典型应用。本质上来看，快速排序应该算是在冒泡排序基础上的递归分治法。

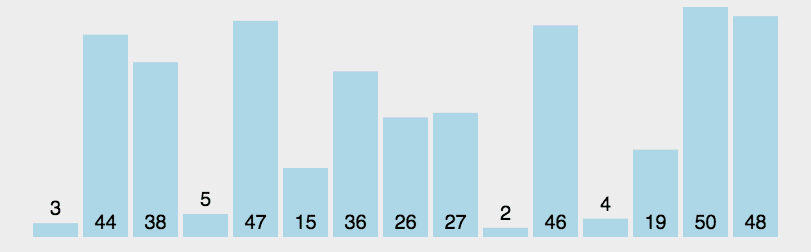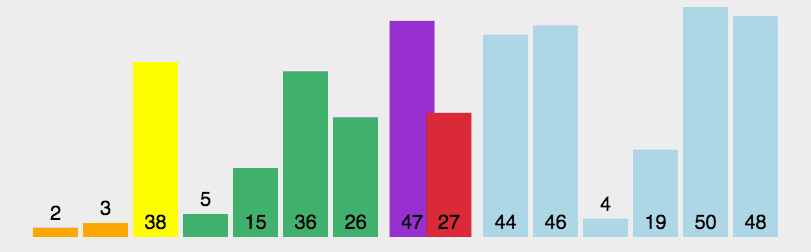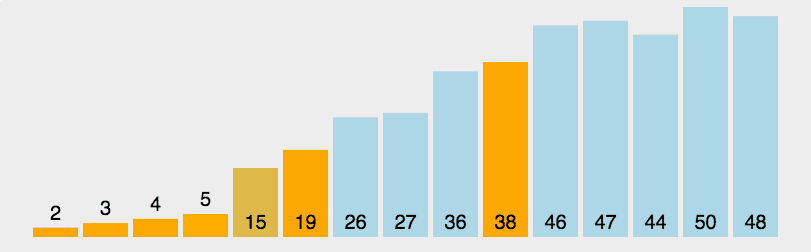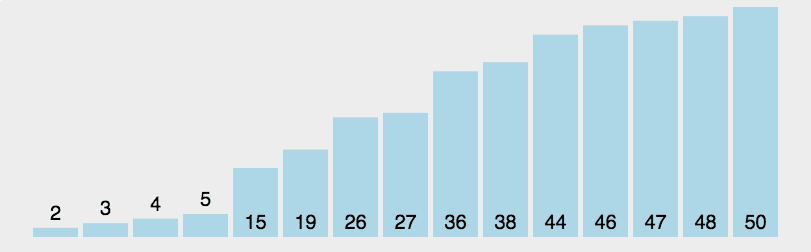
时间复杂度：O(nlog2n)

1. 从数列中挑出一个元素，称为 "基准"（pivot）;
2. 重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作；
3. 递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序；

代码实现：

def QuickSort(array,left,right):
    # 选取数组的一个数为基准数
    i = left
    j = right
    if(left < right):
        pivot = array[left]
        while(left < right):
            # 在找得到比基准小的数之前直从后往前找，否则交换
            while(left < right and array[right] >= pivot): # 当前i的位置为基准值
                right = right -1
            if(left < right):
                swap(array,left,right)
            # 在找到比较基准大的数之前一直从前往后找， 否者交换
            while(left < right and array[left] <= pivot): # 当前j的位置为基准值
                left = left + 1
            if (left < right):
                swap(array, left, right)
      # 递归的进行左右两部分的快排
        QuickSort(array, i, right-1) # 左边
        QuickSort(array, right+1, j) # 右边
    return array

三、 插入排序

        插入排序就是每一步都将一个待排数据按其大小插入到已经排序的数据中的适当位置，直到全部插入完毕。
        插入排序方法分直接插入排序和折半插入排序两种，这里只介绍直接插入排序。
插入排序的平均时间复杂度也是 O(n^2)，空间复杂度为常数阶 O(1)，具体时间复杂度和数组的有序性也是有关联的。

思路：将n个待排序的元素看成一个有序表和一个无序表。开始时有序表只包含一个元  素，无序表中包含n-1个元素
    排序过程每次从无序表中取出第一个元素将他插入到有序表中的适当位置，使之成为新的有序表，重复n-1次可完成排序过程

def InsertSort(array):
    # 外循环，循环获取位排序的数
    for index in range(1,len(array)):
        # 内循环，和有序列表进行比较，从数组第二个数开始
        while(index-1 >= 0):
            # 前一个数大于后一个数就交换
            if(array[index-1] > array[index]):
                swap(array,index-1,index)
                index = index - 1
            else:
               break
    return array

四、希尔排序

        希尔排序也是一种插入排序，它是简单插入排序经过改进之后的一个更高效的版本，也称为缩小增量排序

思路:就是在载入排序外层多了一层循环

代码实现：

def ShellSort(array):
    # 初始化步长
    gap = int(len(array)/2)
    while(gap > 0):
        for i in range(gap,len(array)):
            while(i-1>=0):
                if(array[i-gap] > array[i]):
                    swap(array,i-1,i)
                    # 步长
                    i = i - gap
                else:
                    break
        gap = int(gap/2)
    return array

五、选择排序

 

选择排序（Select Sort） 是直观的排序，通过确定一个 Key 最大或最小值，再从带排序的的数中找出最大或最小的交换到对应位置。再选择次之。双重循环时间复杂度为 O(n^2)

思路：

1. 在一个长度为 N 的无序数组中，第一次遍历 n-1 个数找到最小的和第一个数交换。
2. 第二次从下一个数开始遍历 n-2 个数，找到最小的数和第二个数交换。
3. 重复以上操作直到第 n-1 次遍历最小的数和第 n-1 个数交换，排序完成。

   def SelectSort(array):
       for i in range(len(array)-1):  # 最后一个数字不用比较一定是最大的
           min = array[i]
           min_index = i
           for j in range(i+1,len(array)):
               if(array[j] < min):
                   min = array[j]
                   min_index = j     # 记录比min小的数的下标
               else:
                   continue
           if(min_index != i):  # 如果i位置已经是最小的就用交换
               swap(array, i, min_index)
           else:
               continue
       return array