计算机图形学04:中点Bresenham算法画椭圆
赞
踩

作者:非妃是公主
专栏:《计算机图形学》
博客地址:https://blog.csdn.net/myf_666
个性签:顺境不惰,逆境不馁,以心制境,万事可成。——曾国藩
专栏推荐
专栏系列文章
| 文章名称 | 文章地址 |
|---|---|
| 直线生成算法(DDA算法) | 计算机图形学01——DDA算法 |
| 中点BH算法绘制直线 | 计算机图形学02——中点BH算法 |
| 改进的中点BH算法 | 计算机图形学03——改进的中点BH算法 |
| 中点Bresenham画椭圆 | 计算机图形学04——中点BH绘制椭圆 |
| 中点BH算法绘制任意斜率直线 | 计算机图形学05——中点BH算法绘制任意斜率的直线 |
| 中点Bresenham画圆 | 计算机图形学06——中点BH算法画圆 |
| 有效边表法的多边形扫描转换 | 计算机图形学07——有效边表法绘制填充多边形 |
| 中点BH算法绘制抛物线 100 x = y 2 100x = y^2 100x=y2 | 计算机图形学08——中点BH绘制抛物线 |
| 二维观察之点的裁剪 | 计算机图形学09——二维观察之点裁剪 |
| 二维观察之线的裁剪 | 计算机图形学10——二维观察之线裁剪 |
| 二维观察之多边形的裁剪 | 计算机图形学11——二维观察之多边形裁剪 |
| 二维图形的几何变换 | 计算机图形学12——二维图形几何变换 |
| 三维图形的几何变换 | 计算机图形学13——三维图形几何变换 |
| 三维图形的投影变换 | 计算机图形学14——三维图形投影变换 |
序
计算机图形学(英语:computer graphics,缩写为CG)是研究计算机在硬件和软件的帮助下创建计算机图形的科学学科,是计算机科学的一个分支领域,主要关注数字合成与操作视觉的图形内容。虽然这个词通常被认为是指三维图形,事实上同时包括了二维图形以及影像处理。
一、实现思路
其实曲线微分来看,就是一小段一小段的直线构成的。因此,绘制曲线,其实就是绘制多个直线段,进而实现曲线的绘制(关于对直线的绘制算法原理及代码实现,要查看这篇文章:计算机图形学03:改进的中点BH算法)。
圆也是一样,我们主要采用把他分为四个部分来绘制(按照4个象限去分,每个象限中的部分都相当于一个曲线)。这样,绘制完一个象限,其它部分,就可以简单的通过对称就可以得到了。下面,来看一下详细的步骤。
采用4分法绘制椭圆:
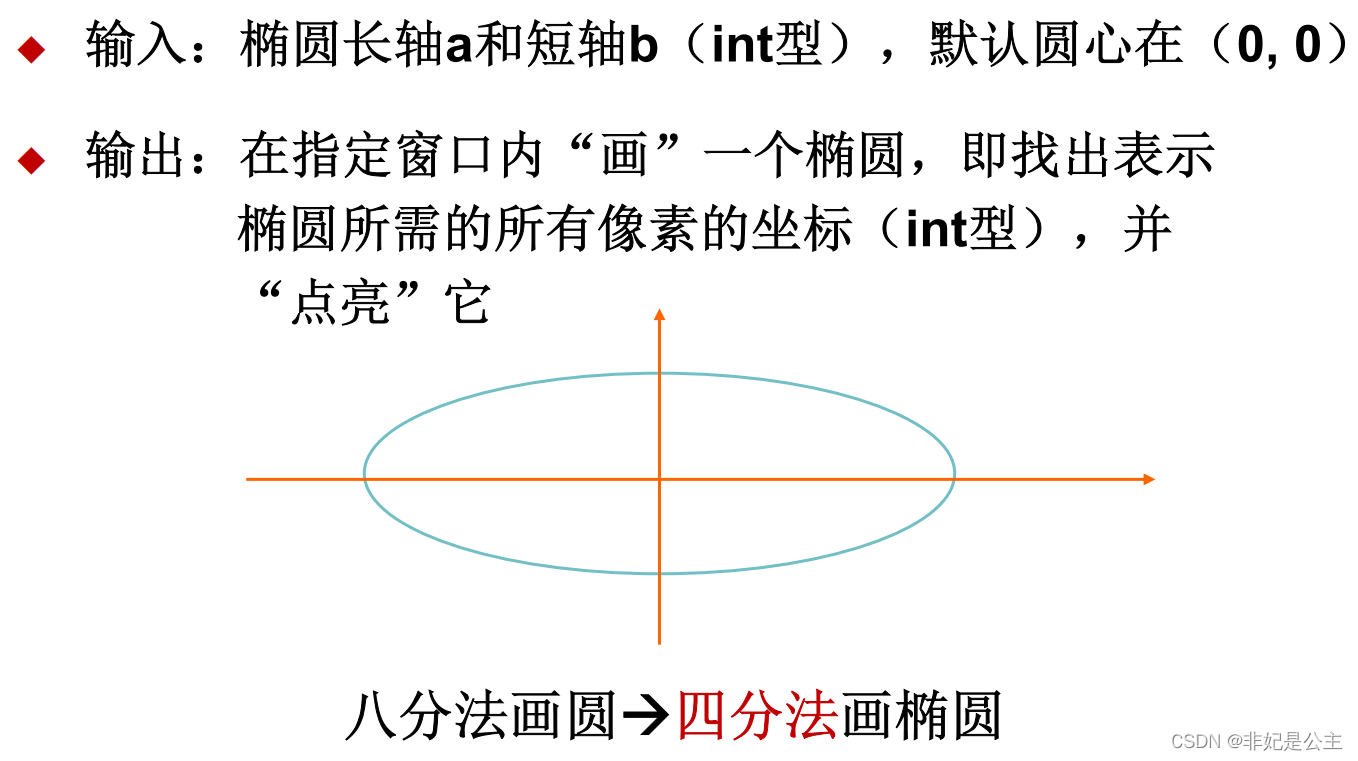
分为两部分绘制:
- 上半部分斜率小于1,x总是+1
- 下半部分斜率大于1,y总是+1
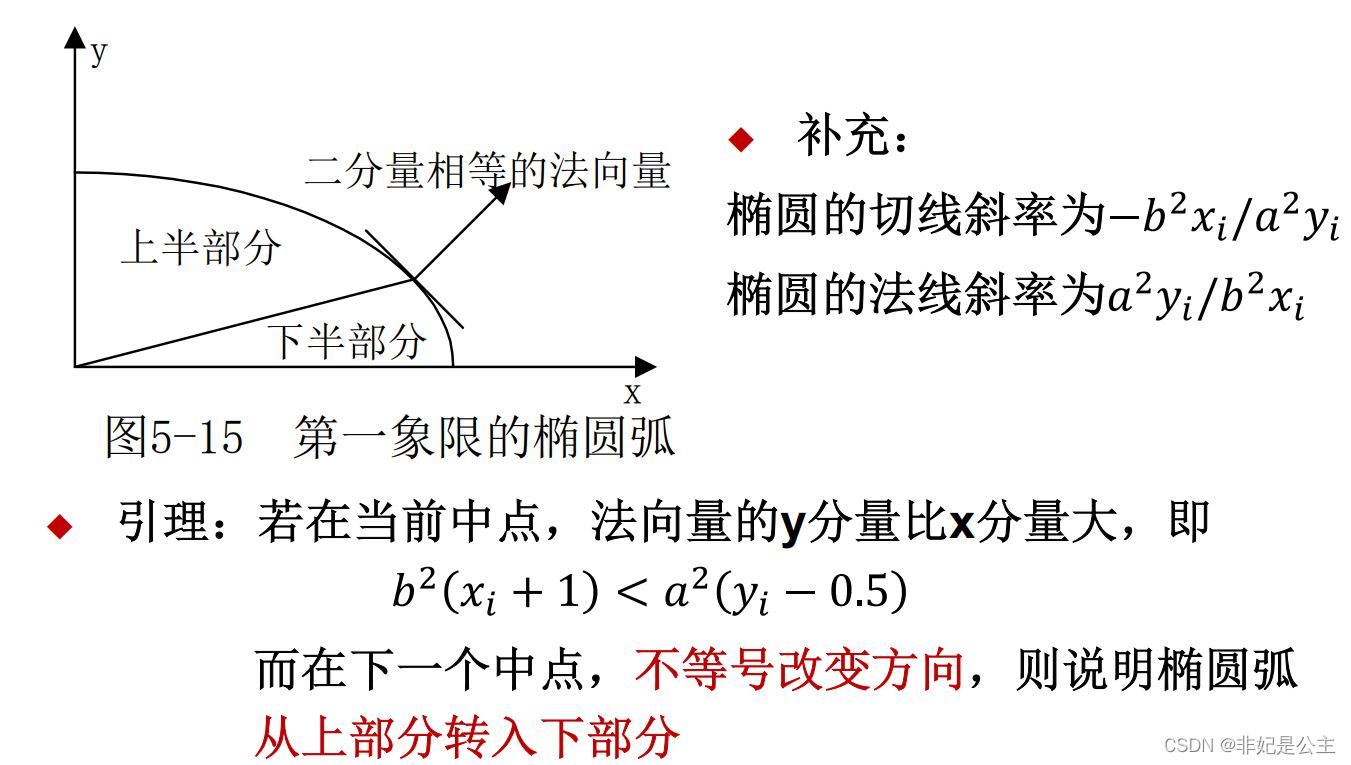

二、算法原理
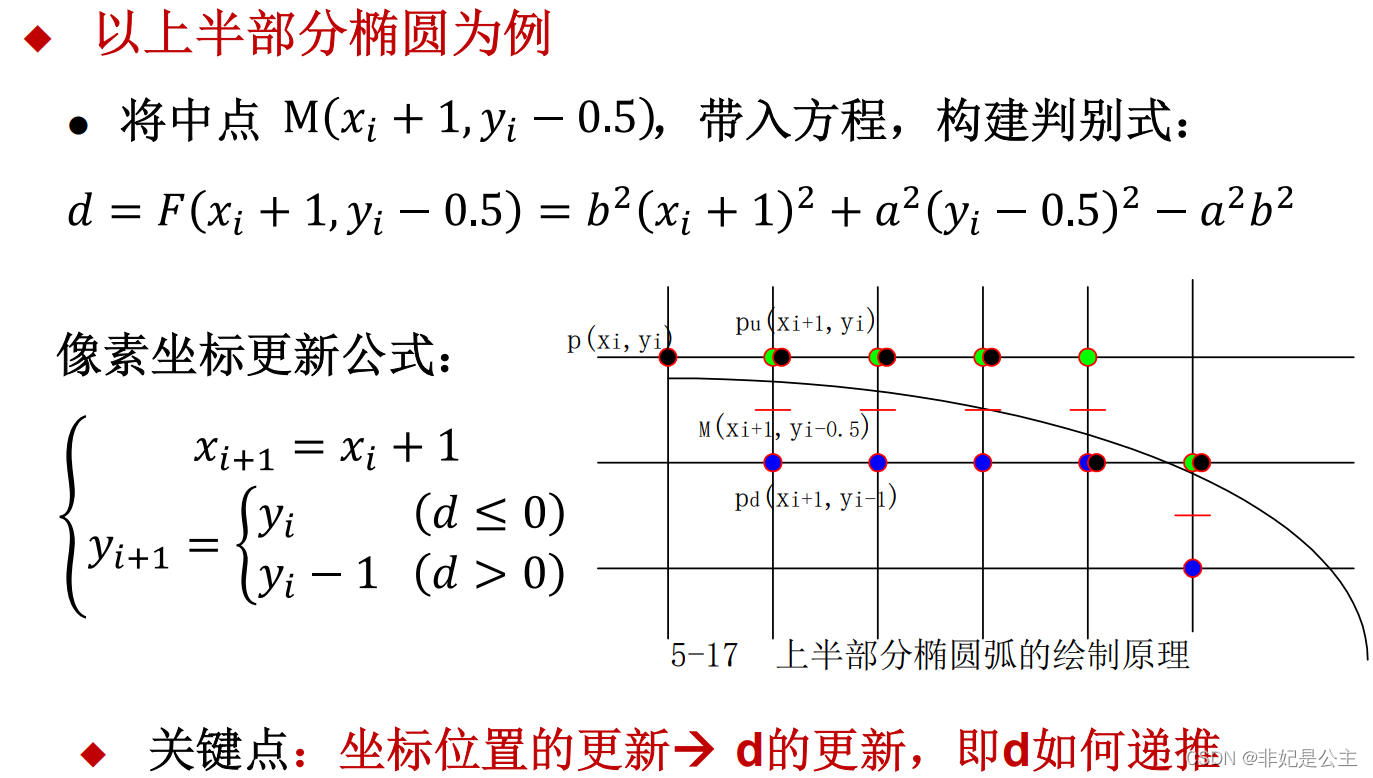


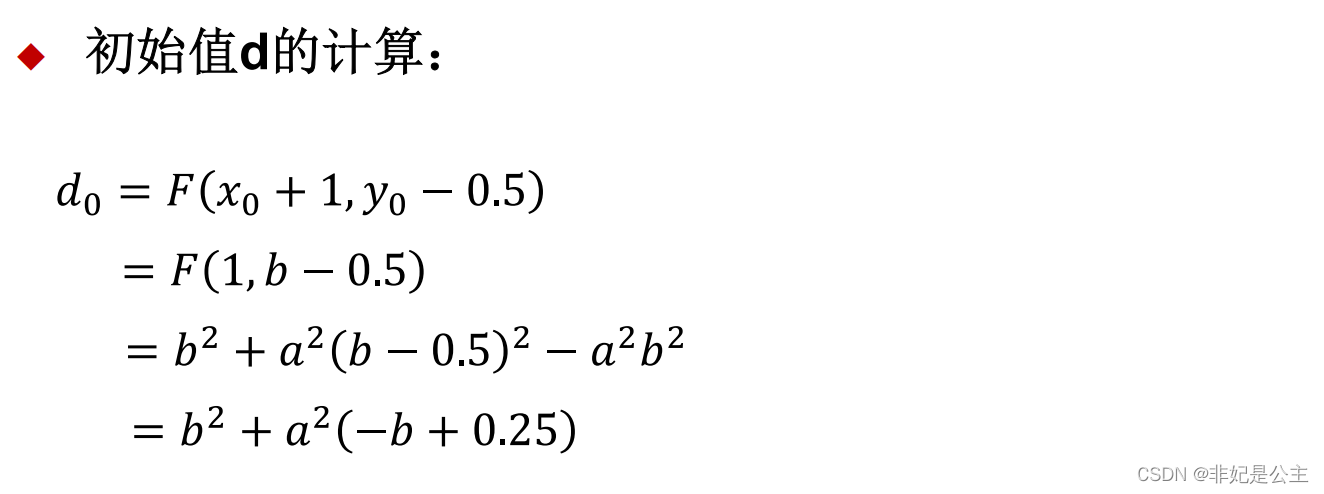

三、OpenGL代码实现代码
// 中点Bh算法绘制椭圆 void MidBhellipse(int a, int b) { int x, y; float d1, d2; x = 0; y = b; d1 = b * b + a * a * (-b + 0.25); glBegin(GL_POINTS); glVertex2i(x, y); glVertex2i(-x, -y); glVertex2i(-x, y); glVertex2i(x, -y); while (b * b * (x + 1) < a * a * (y - 0.5)) { if (d1 <= 0) { d1 += b * b * (2 * x + 3); x++; } else { d1 += b * b * (2 * x + 3) + a * a * (-2 * y + 2); x++; y--; } glVertex2i(x, y); glVertex2i(-x, -y); glVertex2i(-x, y); glVertex2i(x, -y); } /* 上半部*/ d2 = b * b * (x + 0.5) * (x + 0.5) + a * a * (y - 1) * (y - 1) - a * a * b * b; while (y > 0) { if (d2 <= 0) { d2 += b * b * (2 * x + 2) + a * a * (-2 * y + 3); x++; y--; } else { d2 += a * a * (-2 * y + 3); y--; } glVertex2i(x, y); glVertex2i(-x, -y); glVertex2i(-x, y); glVertex2i(x, -y); } glEnd(); }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
四、实现效果图
利用中点BH算法绘制椭圆后,效果如下所示:
the end……
中点Bresenham算法绘制椭圆的内容到这里就要结束啦~~到此既是缘分,欢迎您的点赞、评论、收藏!关注我,不迷路,我们下期再见!!
本文内容由网友自发贡献,转载请注明出处:【wpsshop博客】
- 本篇文章主要介绍了C++中模板的特化。【C++干货铺】非类型模板|模板特化|模板分离编译=========================================================================个人主... [详细]
赞
踩
- 报错为“error:‘B’doesnotnameatype”,就是因为在A类中使用B*b之前没有声明或定义B类,如果在第一行加上一句前置声明“classB;”,就不会有这样的问题了。C++编译报错:doesnotnameatype在一个源文... [详细]
赞
踩
- 【STL】string类(上)&<vector>和<list>的简单使用什么是STL 二,STL的六大组件 三,标准库中的string类 1,string类 2,string类的常用接口 1,string类对象的常见构造 2,s... [详细]
赞
踩
- 2048小游戏代码及总结_c语言2048游戏课程总结c语言2048游戏课程总结****大学《程序设计课程设计》报告1课程设计需求编写一个2048游戏,且使用图形界面。游戏规则为:①游戏开始时,初始化一个16方格的棋盘,并在棋盘内随机出现两个... [详细]
赞
踩
- 时间复杂度计算的是一个算法中的基本操作的执行次数,它的计算遵循大O的渐进表示法_数据结构时间复杂度怎么计算数据结构时间复杂度怎么计算前言 大家好啊,这里是幸麟一名普通的大学牲... [详细]
赞
踩
- 【STL】手撕string类目录 1,string类框架 2,string(构造) 3,~string(析构) 4,swap(交换) 5,string(拷贝构造) 1,常规法 2,简便法 6,size(字符长度) 7,c_str(返回字... [详细]
赞
踩
- 引用也是C++中的一种数据类型,它提供了一种简洁而高效的方式来操作变量和对象,而不需要拷贝它们本身。引用被视为原变量的一个别名,其操作类似于指针,但是引用不能被赋值为NULL,也不能进行指针运算。虚函数是C++中的一种特殊函数,它可以实现多... [详细]
赞
踩
- 严蔚敏版【数据结构】1.邻接矩阵表示法:无向图的邻接矩阵、有向图的邻接矩阵、网的邻接矩阵、邻接矩阵创建无向网2.邻接表:无向图的邻接表、有向图的邻接表、图的邻接表存储表示、邻接表示法创建无向图3.十字链表4.邻接多重表_图的存储结构图的存储... [详细]
赞
踩
- 本篇博客仅仅实现存储字符(串)的string同时由于C++string库设计的不合理,我仅实现一些最常见的增删查改接口接下来给出的接口都是基于以下框架:private: char*_str;//思考如何不用const size_t_si... [详细]
赞
踩
- 利用string的一些常用方法解题,本篇文章不乏有你眼前一亮的优秀方法,欢迎大家订阅。【LeetCode】【C++】stringOJ必刷题... [详细]
赞
踩
- 第三步:编写头文件(重点)_vs调用动态库dllvs调用动态库dll转载地址前言:查了好久好久网上的资料C++调用动态链接库,试了好多方法(直接创建DLL、空项目创建的)都多多少少有些问题,最后自己不断摸索着成功了,还是很开心的,接下来把最... [详细]
赞
踩
- static_cast用法... [详细]
赞
踩
- 以上是自己学习CMake的一点学习记录,通过简单的例子让大家入门CMake,学习的同时也阅读了很多网友的博客。CMake的知识点还有很多,具体详情可以在网上搜索。总之,CMake可以让我们不用去编写复杂的Makefile,并且跨平台,是个非... [详细]
赞
踩
- 偏最小二乘的r语言实现,及主成分选取的规则_r语言偏最小二乘回归分析r语言偏最小二乘回归分析首先打开Rstudio,点击tools—>globaloptions创建工作环境这部分设置工作目录,一般数据和结果就放这里面。a<-re... [详细]
赞
踩
- C++分别利用三种动态规划解决最长公共子序列问题_最长公共子序列最长公共子序列这里,为了更方便地解释,我以洛谷上的一道典型题目为例,为大家讲解处理最长公共子序列问题的几种常见方法。这道题目中规定了两个子序列的长度相等,如果遇到不等的情况,也... [详细]
赞
踩
- list的底层与vector和string不同,实现也有所差别,特别是在迭代器的设计上,本节将为大家介绍list简单实现,并揭开list迭代器的底层!list模拟实现到这里就介绍了,本篇我们简单介绍了一下list的增删功能实现(与链表差别不... [详细]
赞
踩
- 1.关联式容器在初阶阶段,我们已经接触过STL中的部分容器,比如:vector、list、deque、forward_list(C++11)等,这些容器统称为序列式容器,因为其底层为线性序列的数据结构,里面存储的是元素本身。那什么是关联式容... [详细]
赞
踩
- 模拟实现简易vector【STL】模拟实现简易vector目录1.读源码2.框架搭建3.vector的迭代器4.vector的拷贝构造与赋值拷贝构造赋值5.vector的常见重要接口实现operator[]的实现insert接口的实现era... [详细]
赞
踩
- 在C++中,模板是一种泛型编程(GenericProgramming)的工具,它允许程序员编写通用的、与数据类型无关的代码。使用模板,你可以编写函数或类,使其能够适用于多种数据类型而不需要重复编写多份相似的代码。函数模板允许你编写一个通用的... [详细]
赞
踩
- 本文主要介绍了将sklearn转换成c/c++的实战代码,希望对将sklearn模型进行部署的同学们有所帮助。文章目录1.背景描述2.安装方法3.实战代码3.1训练转换+预测的完整代码3.2生成c/c++可加载的模型文件3.3加载新生成的模... [详细]
赞
踩
Copyright © 2003-2013 www.wpsshop.cn 版权所有,并保留所有权利。




