剑指Offer C++ --- 数组篇2

12.矩阵中的路径

思路：

从矩阵第一个元素开始判断，它是不是word的第一个字符，如果不是，继续判断下一个

如果是，则判断其上，下，左，右只要有一个满足，其是word的第一个字符，继续判断下一个。。。 如果不是，则回到矩阵的位置，继续判断下一个是不是word的开始字符

很明显，要用回溯算法，进行深度遍历

int row;
int col;
 
bool exist(vector<vector<char>>&board, string word)
{
    row = board.size();
    col = board[0].size();
    for(int i = 0; i < row; ++i)
    {
        for(int j = 0; j < col; ++j)
        {
            if(dfs(board,word,i,j,0))
            {
                return true;
            }
        }
       
    }
    return false;
}
 
 
 
bool dfs(vector<vector<char>>&board,string& word,int i,int j,int k)
{
    //矩阵中的字母不合适退出
    if(i<0 || i>=row || j<0 || j>=col || board[i][j] != word[k])
    {
        return false;
    }
 
    //完全匹配成功
    if(word.size()-1 == k)
    {
        return true;
    }
 
    //能走到这儿，说明board[i][j]的字母与word的字母匹配成功
    //board[i][j]置为'\0'
    board[i][j] = '\0';
    
    //上 下 左  右进行深度探索
    bool res = dfs = (board,word,i+1,j,k+1) || (board,word,i-1,j,k+1) 
                     || (board,word,i,j-1,k+1) || (board,word,i,j+1,k+1);
    
    //回溯过程中，将矩阵中修改的元素重新填回
    board[i][j] = word[k];
 
    return res;
}
 

13.打印从1到最大的n位数

vector<int> printNumbers(int n)
{
   int max = pow(10,n) - 1;
   vector<int> nums;
   nums.reserve(max);
   
   for(int i = 1; i <= max; ++i)
   {
       nums.emplace_back(i);
   }
 
   return nums;
} 

14.调整数组顺序使奇数位于偶数之前

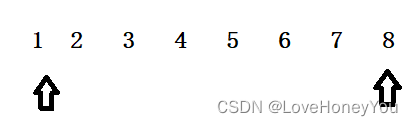
思路：首尾开工

    vector<int> exchange(vector<int>& nums) 
    {
        int i = 0;
        int j = nums.size()-1;
        
        while(i<j)
        {
            //遇到奇数直接跳过
            while(i<j && (nums[i] & 1) == 1)
            {
                ++i;
            }
          
            //遇到偶数直接跳过
            while(i<j && (nums[j] & 1) == 0)
            {
                --j;
            }
            
            //交换
            if(i < j)
            {
               int tmp = nums[i];
               nums[i] = nums[j];
               nums[j] = tmp;
               ++i;
               --j;
            }
        }
 
        return nums;
    }

15.顺时针打印矩阵

思路：

转化四种状态：

left  ---》 right

top  ---》 bottom

right  ---》left

bottom  ---》 top

退出条件：左边界 > 右边界，上边界 > 下边界

每遍历一次就需要检查一次是否越界

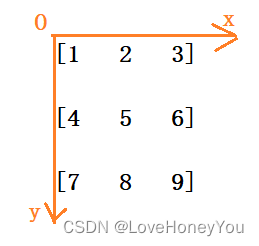
vector<int> spiralOrder(vector<vector<int>>& matrix)
{
    //控制列
    int left = 0; //左边界
    int right = matrix[0].size()-1; //右边界
    
    //控制行
    int top = 0;  //上边界
    int bottom = matrix.size()-1;  //下边界
    
    vector<int> vec;
    vec.reserve((right+1)*(bottom+1));
    
    while(true)
    {
      //left -> right
      for(int i = left;i<=right;++i)
      {
         vec.emplace_back(matrix[top][i]);
      }
      
      //检查边界，并跳到下一行
      if(++top > bottom)  break;
      
      //top -> bottom
      for(int i = top;i<=bottom;++i)
      {
          vec.emplace_back(matrix[i][right]);
      }
      
      //检查边界，并跳到下一列
      if(--right < left)  break;
      
      //right -> left
      for(int i = right;i>=left;--i)
      {
          vec.emplace_back(matrix[bottom][i]);
      }
 
      //检查边界，并跳到上一行
      if(--bottom < top)  break;
 
      //bottom -> top
      for(int i = bottom;i>=top;--i)
      {
          vec.emplace_back(matrix[left][i]);
      }
       
      //检查边界，并跳到下一列
      if(++left > right)  break;
    }
 
    return vec;
 
}

16.栈的压入、弹出序列

思路：

借助栈来判断，每向栈内入一个元素，循环判断栈顶元素是否与出栈序列的元素相等，如果相等则出栈，序列向后迭代一个，继续比较。。。

如果栈为空，则出栈序列正确，否则错误

bool validateStackSequences(vector<int>& pushed, vector<int>& popped)
{
    statct<int> st;
    int i = 0;
 
    for(auto x:pushed)
    {
       st.push(x);    
       while(!st.empty() && st.top() == popped[i])
       {
            st.pop();
            i++;
       }
    }
    return st.empty();
}

17.数组出现次数超过一半的数字

思路：假设众数val = x，num = 1，遍历后续元素，如果相等则num+=1，如果不相等，则num -=1

当num = 0时，下一个遍历的元素即就是x，num重新赋值为1

int majorityElement(vector<int>& nums)
{
    int x = 0;
    int n = 0;
 
    for(auto val : nums)
    {
        if(n == 0)
        {
           x = val;
           n = 1;
        }
        else
        {           
           x != val ? n -= 1 : n += 1;
        }
    }
    return x;
} 

18.最小的k个数

思路：利用优先级队列构建小根堆，然后取堆顶前k个元素

vector<int> getLeastNumbers(vector<int>& arr, int k)
{
    if(k == 0)
    {
       return vector<int>();
    }
 
    //构建小根堆
    priority_queue<int,vector<int>,greater<int>> q;
    for(auto x : arr)
    {
       q.push(x);
    }
 
    vector<int> vec;
    vec.reserve(k);
    
    while(k-- != 0)
    {
       vec.emplace_back(q.top));
       q.pop();  
    }
    return vec;
} 

19.有硬币1，3，5若干，求组成金额为11的最小的硬币数

//分治
int func(int n)
{
    if(n == 1 || n == 3 || n == 5)
    {
        return 1;
    }
    
    else if(n == 2 || n == 4)
    {
        return 2;
    }
 
    else
    {
        int n1 = func(n-1)+1;
        int n2 = func(n-3)+1;
        int n3 = func(n-5)+1;
        return min({n1,n2,n3});
    }
}
 
//动态规划
void fun()
{
    int v[] = {1,3,5}; //硬币的面额组成
    int length = sizeof(v)/sizeof(v[0]);
    int c = 11;  //面值11
 
    int dp[12]{}; //dp数组，存放最优子结构
    
    for(int i = 1; i <= c; ++i)
    {
        dp[i] = i;    //表示初始全部由1分硬币组成
        for(int j = 0; j < length; ++j)
        {
           if(i >= v[j] && (1 + dp[i-v[j]]< dp[i]]))
           dp[i] = 1+dp[i-v[j]];
        }
    }
         
    cout << dp[c] << endl;
    return 0;
}

动态规划的核心思想：将子问题的最优子解存下来，在求取后续子问题时，可以进行复用

20. 斐波那契数列

a.分治

int fib(int n) 
{
    if(n == 0)
    {
       return 0;
    }
    else if(n == 1)
    {
       return 1;
    }
    else
    {
       return fib(n-2)+fib(n-1);
    }
}

b.动态规划（递归）

    int fib(int n)
    {
       vector<int> dp(n+1,-1);
       return fib(dp,n);
    }
 
    int fib(vector<int>& dp,int n)
    {
        if(dp[n] != -1)
        {
            return dp[n];
        }
 
        if(n == 0)
        {
            dp[n] = 0;
            return dp[n];
        }
        else if(n == 1)
        {
            dp[n] = 1;
            return dp[n];
        }
        else
        {
            dp[n] = fib(n-2) + fib(n-1);
            return dp[n];
        }
        return dp[n];
    }

c.动态规划（非递归）

    int fib(int n) 
    {
       //状态数组
       vector<int> dp(n+2,-1);
       //dp[0] = 0, dp[1] = 1, dp[i] = dp[i-2] + dp[i-1] (i>2)
       dp[0] = 0;
       dp[1] = 1;
 
       if(n == 0 || n == 1)
       {
           return dp[n];
       }
 
       for(int i = 2;i<=n;++i)
       {
          dp[i] = dp[i-2]+dp[i-1];
       }
       return dp[n];
    }