《剑指offer》刷题技巧(c++版)

剑指 Offer 06. 从尾到头打印链表

使用vector的insert函数，通过头插法插入到数组中

iterator insert (const_iterator position, const value_type& val);

iterator insert (const_iterator position, size_type n, const value_type& val);

template <class InputIterator>
iterator insert (const_iterator position, InputIterator first, InputIterator last);

iterator insert (const_iterator position, value_type&& val);

iterator insert (const_iterator position, initializer_list<value_type> il); 

剑指 Offer 07. 重建二叉树

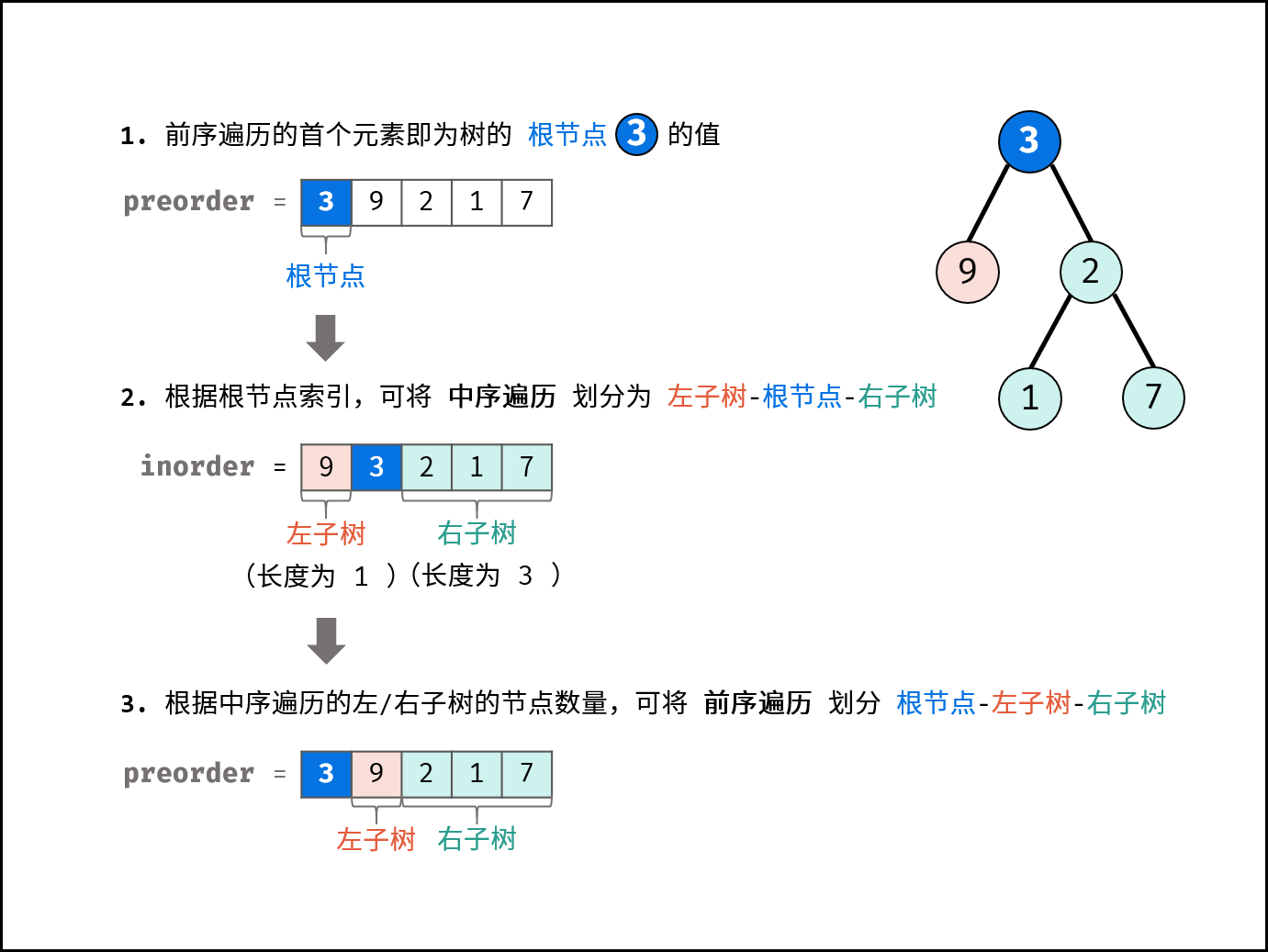
代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        this->preorder=preorder;
        for(int i=0;i<inorder.size();i++)
            dic[inorder[i]]=i;
        return createChild(0,0,inorder.size()-1);
    }
private:
    vector<int> preorder;
    unordered_map<int,int> dic; //存储中序遍历位置
    TreeNode* createChild(int root,int left,int right){
        if(left>right) return nullptr;
        TreeNode * node=new TreeNode(preorder[root]);//建立根节点
        int i=dic[preorder[root]];//找到根节点在中序遍历中的位置
        node->left=createChild(root+1,left,i-1);
        node->right=createChild(root+i-left+1,i+1,right);
        return node;
    }
 
};

剑指 Offer 09. 用两个栈实现队列

栈无法实现队列功能： 栈底元素（对应队首元素）无法直接删除，需要将上方所有元素出栈。
双栈可实现列表倒序： 设有含三个元素的栈 A = [1,2,3]A=[1,2,3] 和空栈 B = []B=[]。若循环执行 AA 元素出栈并添加入栈 BB ，直到栈 AA 为空，则 A = []A=[] , B = [3,2,1]B=[3,2,1] ，即 栈 BB 元素实现栈 AA 元素倒序 。
利用栈 BB 删除队首元素： 倒序后，BB 执行出栈则相当于删除了 AA 的栈底元素，即对应队首元素。

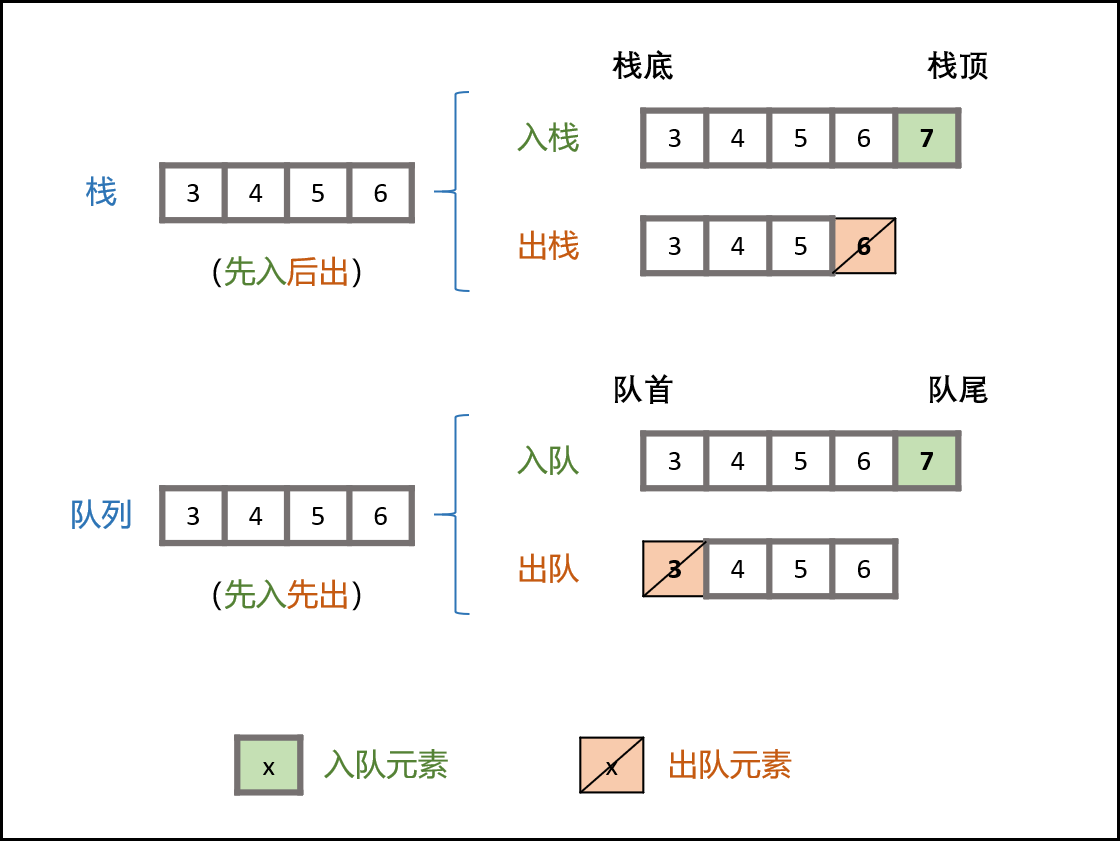
STL中 stack的常用函数：

stack<T> stack;

stack.pop();  stack.push(T t);  stack.empty();

解题代码：

class CQueue {
public:
    CQueue() {
        
    }
    
    void appendTail(int value) {
        while(!st1.empty()){
            //put all of st1 into st2
            
            st2.push(st1.top());
            st1.pop();
        }
        st2.push(value);
        while(!st2.empty()){
            st1.push(st2.top());
            st2.pop();
        }
    }
    
    int deleteHead() {
        if(st1.empty()){
            return -1;
        }
        int temp=st1.top();
        st1.pop();
        return temp;
    }
private:
    stack<int> st1;
    stack<int> st2;
};
 
/**
 * Your CQueue object will be instantiated and called as such:
 * CQueue* obj = new CQueue();
 * obj->appendTail(value);
 * int param_2 = obj->deleteHead();
 */

剑指 Offer 10- I. 斐波那契数列

注意int类型溢出问题

class Solution {
public:
    int fib(int n) {
        if(n==0) return 0;
        if(n==1) return 1;
        int a=0,b=1;
        for(int i=2;i<=n;i++){
            int temp=b;
            int sum=(a+b)%1000000007;
            a=temp;
            b=sum;
        }
        return b%(1000000007);
    }
};

剑指 Offer 10- II. 青蛙跳台阶问题

 与斐波那契数列为题相同，为动态规划问题，只需要把n=0的值改为1即可

class Solution {
public:
    int numWays(int n) {
       if(n==0) return 1;
        if(n==1) return 1;
        int a=1,b=1;
        for(int i=2;i<=n;i++){
            int temp=b;
            int sum=(a+b)%1000000007;
            a=temp;
            b=sum;
        }
        return b%(1000000007);
        
    }
};

剑指 Offer 11. 旋转数组的最小数字

可以使用二分法来减少运行时间，但是直接遍历也能通过

class Solution {
public:
    int minArray(vector<int>& numbers) {
        //试试用普通方式
        int temp=numbers[0];
        for(int i=0;i<numbers.size();i++){
            if(numbers[i]<temp)
            return numbers[i];
        }
        return temp;
    }
};

剑指 Offer 12. 矩阵中的路径

解题思路：
本问题是典型的矩阵搜索问题，可使用 深度优先搜索（DFS）+ 剪枝 解决。

深度优先搜索： 可以理解为暴力法遍历矩阵中所有字符串可能性。DFS 通过递归，先朝一个方向搜到底，再回溯至上个节点，沿另一个方向搜索，以此类推。
剪枝： 在搜索中，遇到 这条路不可能和目标字符串匹配成功 的情况（例如：此矩阵元素和目标字符不同、此元素已被访问），则应立即返回，称之为 可行性剪枝 。

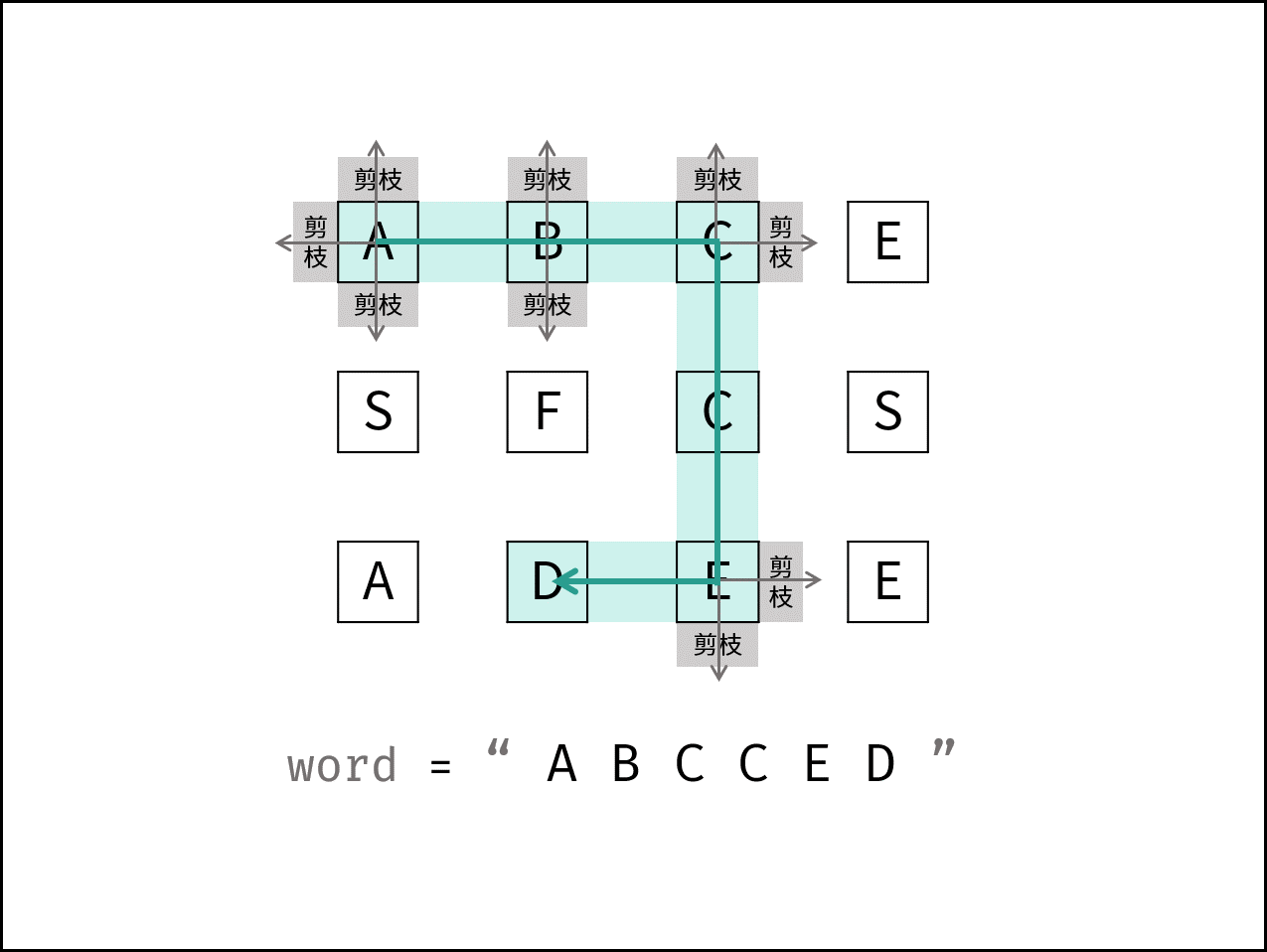
class Solution {
public:
    bool exist(vector<vector<char>>& board, string word) {
        rows=board.size();
        cols=board[0].size();
        for(int i=0;i<rows;i++){
            for(int j=0;j<cols;j++){
                if(dfs(board,word,i,j,0))return true;
            }
        }
        return false;
    }
private:
    int rows,cols;
    bool dfs(vector<vector<char>>& board,string word,int i,int j,int k){
        if(i>=rows||i<0||j>=cols||j<0||board[i][j]!=word[k])return false;
        if(k==word.size()-1)return true;
        board[i][j]='\0';
        bool res=dfs(board,word,i+1,j,k+1)||dfs(board,word,i-1,j,k+1)||
                dfs(board,word,i,j+1,k+1)||dfs(board,word,i,j-1,k+1);
        board[i][j]=word[k];  
        return res;
        }
};