- 1❤ error: RPC failed; curl 92 HTTP/2 stream 0 was not closed cleanly: PROTOCOL_ERROR (err 1)_error: rpc failed; curl 92 http/2 stream 0 was not
- 2Jetson Nano B01部署YOLOv5项目全流程(五)TensorRT加速配置_yolov5 jetson nano
- 3高效翻译工具GPT插件的使用教程_知云文献翻译引入gpt
- 4阅读笔记-阿里妈妈AI智能文案_阿里 ai智能文案
- 5Java导出Word文档的实现_xdocreportregistry.loadreport()
- 6零基础入门Jetson Nano——Yolov5+TensorRT+Deepstream_jetson yolov5
- 7构建异步高并发服务器:Netty与Spring Boot的完美结合_springboot3 集成netty
- 8Golang中结构体-类、封装、继承_golang 结构体继承
- 9mysql进阶-执行计划
- 10解锁数据分析的神器:ChatGPT引领人工智能革命
最大子段和——用蛮力算法,分治策略,动态规划算法三种求法(C语言)_最大子段和问题的动态规划算法
赞
踩
目录
一、题目
设A=<a1,a2,...,an>是n个整数的序列,称<ai,....,aj>为该序列的连续子序列,其中1<=i<=j<=n,子序列的元素之和称为A的子段和:
例如,A=<-2,11,-4,13,-5,-2>,那么它的子段和如下:
长度为1的子段和有:-2,11,-4,13,-5,-2
长度为2的子段和有:9,7,9,8,-7
长度为3的子段和有:5,20,4,6
长度为4的子段和有:18,15,2
长度为5的子段和有:13,13
长度为6的子段和有:11
其中的最大子段和为:11-4+13=20
则最大子段和问题为:
给定n个整数的序列A=<a1,a2,...,an>,求
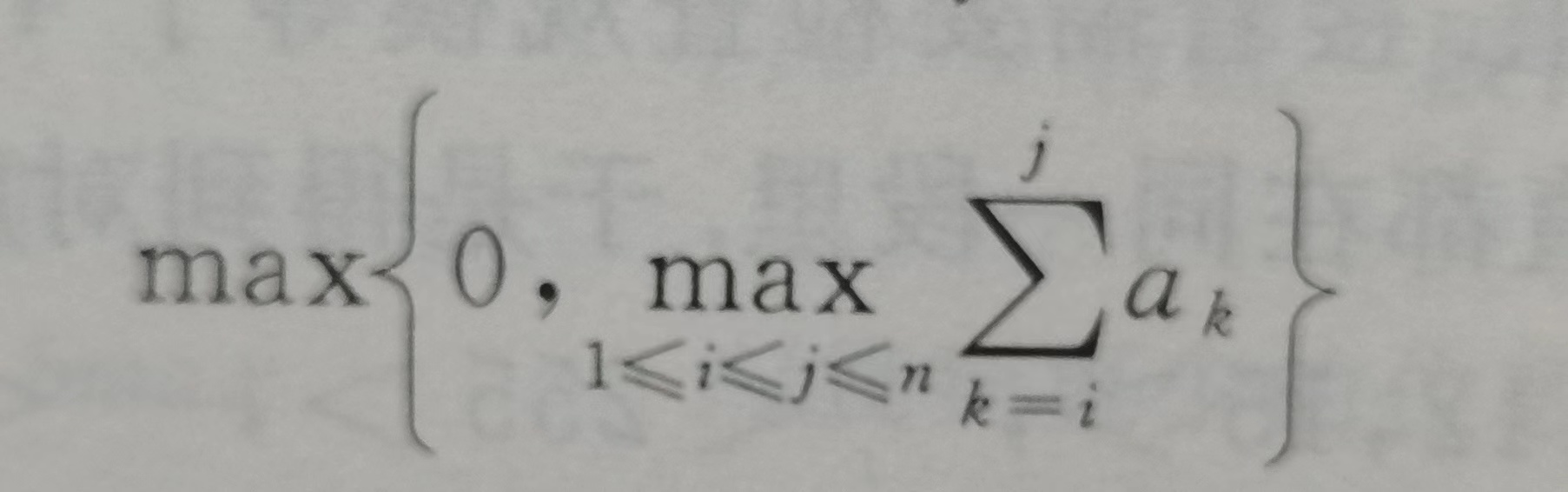
二、算法求解
1、蛮力算法
通过枚举A的所有连续子序列并且求和,通过比较找出具有最大和的子序列。
伪代码
//算法 Enumerate
//输入:数组A[1..n]
//输出:sum,first,last //sum为最大子段和,first与last分别是和的首末位置
算法分析
3个for循环,每次执行O(n)次,循环内部是常数操作,所以该算法的时间复杂度为
程序
- //算法3.8 Enumerate
- //输入:数组A[1..n]
- //输出:sum,first,last
-
- #include<stdio.h>
- #include<stdlib.h>
- void Enumerate (int a[],int n)
- {
- int sum = 0;
- int i,j,k;
- int first,last;
- for(i = 0;i < n; i++){
- for(j = i;j < n;j++){
- int thissum = 0;
- for(k = i;k <= j; k++){
- thissum = thissum + a[k];
- }
- if(thissum > sum){
- sum = thissum;
- first = i;
- last = j;
- }
- }
- }
- printf("数组A的最大连续子段和为A[%d..%d]=%d",first+1,last+1,sum);
- }
-
- int main()
- {
- int A[6]={-2,11,-4,13,-5,-2};
- int i;
- for(i = 0;i < 6;i++)
- {
- printf("%d ",A[i]);
- }
- printf("\n");
- Enumerate(A,6);
- return 0;
- }

2、分治策略
与最邻近点对的算法(参考之前的文章)类似,我们可以在 n/2的位置将 A 划分成A1和 A2前后两半,于是 A 的最大子段和可能是三种情况:
- 出现在 A1部分
- 出现在 A 部分,
- 出现在横跨两边的中间部分
前两种情况恰好对应于两个规模减半的子问题,第三种情况需要特殊处理一下,设原问题的输人是 A [1...n],中间分点 k = n /2,那么前半部分子问题的输人是 A [1...k],后半部分子问题的输人是 A [ k +1,n]。在第三种情况下,设这个最大和是 A [ p .. q ],那么,
,从 A [ p ]到 A [ k ]的元素都在 A1 中,从 A [ k 十1]到 A [ q ]的元素都在 A2 中,我们只需要从 A [ k ]和 A [ k +1]分别向前和向后求和即可,比如以 A [ p ...k ]的计算为例,依次计算 A [ k .. k ], A [ k-1, k ],.., A [1...k],记下其中最大的和 S1 ,即 A [ p ... k ],对右半部可以同样处理,只不过扫描方向相反,得到的 S2 就是 A [ k+1... q ]的元素之和,当两个方向的扫描都完成之后,S1+S2 就是横跨中心的最大和,其边界从p到q。这三种情况都计算完成以后,通过比较就可以确定 A 的最大子段和
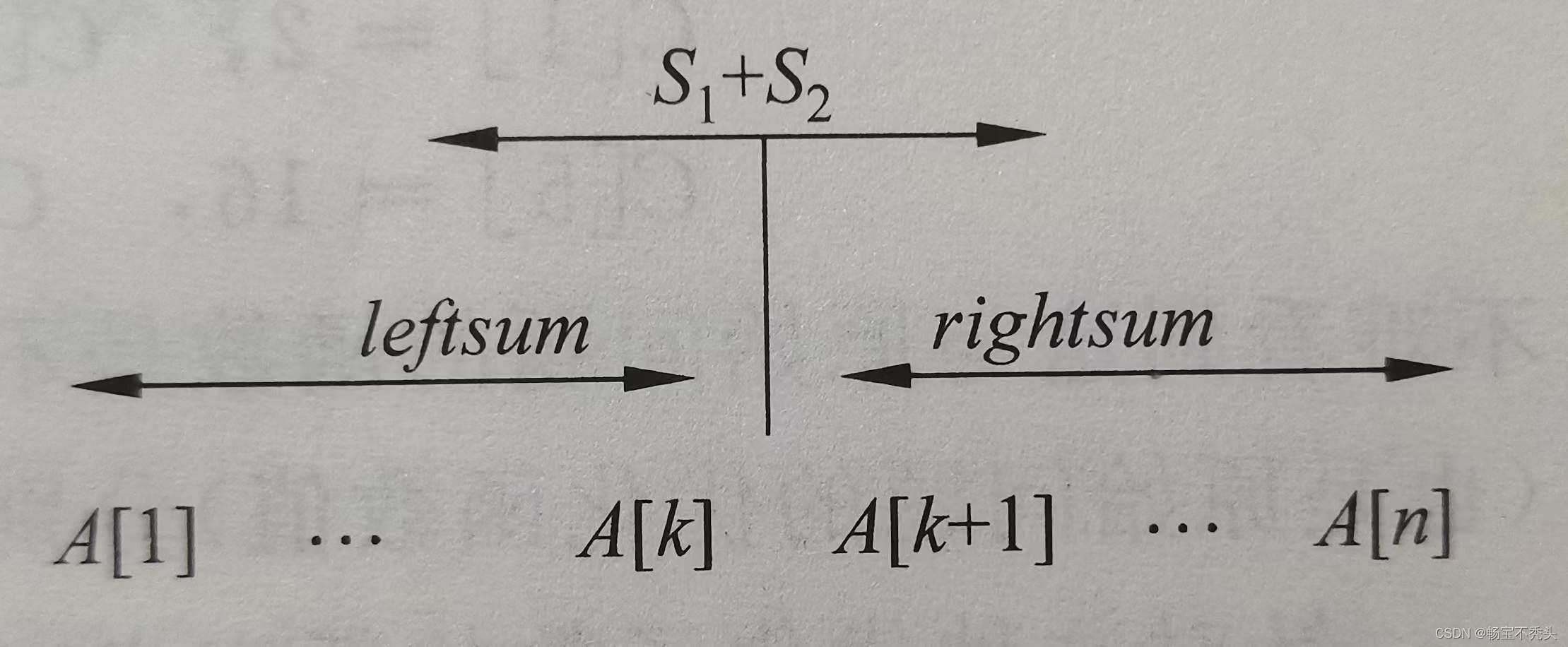
伪代码
//MaxSubSum(A,left,right) 【分治算法】
//输入:数组A,left,right分别是A的左右边界,1<=left<=right
//输出:A的最大子段和sum及其子段的前后边界
算法分析
设算法对规模为的输人运行时间是 T ( n ),行3和行4是递归调用,每个子问题是原来问题规模的一半,因此需要2T( n /2)时间,行5和行6的处理需要扫描A的每个元素,总计需要O(n)时间,于是递归方程为:
该方程的解为:
程序
- //算法3.9 MaxSubSum(A,left,right) 【分治算法】
- //输入:数组A,left,right分别是A的左右边界,1<=left<=right
- //输出:A的最大子段和sum及其子段的前后边界
-
- #include<stdio.h>
- #include<stdlib.h>
-
- typedef struct max_info{
- int low;
- int high;
- int sum;
- };
-
- struct max_info MaxSubSum(int a[],int left,int right)
- {
- struct max_info maxinfo;
- maxinfo.sum = 0;
- int i;
- if(left == right){
- maxinfo.sum = a[left]>0 ? a[left] : 0;
- maxinfo.high = right;
- maxinfo.low = right;
- return maxinfo;
- }
- else{
-
- struct max_info leftinfo;//左侧
- struct max_info rightinfo;//右侧
- struct max_info croseinfo;//跨越
-
-
- int center = (left + right) / 2;
- leftinfo = MaxSubSum(a, left, center);
- rightinfo = MaxSubSum(a, center + 1, right);
-
-
- int s1 = 0;
- int suml = 0;
- for(i = center; i >= left; i--)
- {
- suml += a[i];
- if(suml > s1)
- {
- s1 = suml;
- croseinfo.low = i;
- }
- }
-
- int s2 = 0;
- int sumr = 0;
- for(i = center + 1; i < right; i++)
- {
- sumr += a[i];
- if(sumr > s2)
- {
- s2 = sumr;
- croseinfo.high = i;
- }
-
- }
- croseinfo.sum = s1 + s2;
- if(croseinfo.sum < leftinfo.sum){
- maxinfo.sum = leftinfo.sum;
- maxinfo.high = leftinfo.high;
- maxinfo.low = leftinfo.low;
- }
- if(croseinfo.sum < rightinfo.sum){
- maxinfo.sum = rightinfo.sum;
- maxinfo.high = rightinfo.high;
- maxinfo.low = rightinfo.low;
- } else{
- maxinfo.sum = croseinfo.sum;
- maxinfo.high = croseinfo.high;
- maxinfo.low = croseinfo.low;
- }
-
- }
- return maxinfo;
- }
-
- int main()
- {
- struct max_info maxinfo;
- int A[6]={-2,11,-4,13,-5,-2};
- int i;
- for(i = 0;i < 6;i++)
- {
- printf("%d ",A[i]);
- }
- printf("\n");
- maxinfo = MaxSubSum(A,0,5);
- printf("数组A的最大连续子段和为:A[%d..%d]=%d\n",maxinfo.low+1,maxinfo.high+1,maxinfo.sum);
- return 0;
- }

3、动态规划算法
为了得到更高效的算法,我们需要在子问题之间建立一个简单的递推关系,因此定义一个优化函数
![]()
对于数组A=<2,-5,8,11,-3,4,6>,其优化函数为:C[1]=2、C[2]=-3、C[3]=8、C[4]=19、C[5]=16、C[6]=20、C[7]=26
在这种优化函数中,C [ i +1]可以通过 C[ i ] 直接得到,因为如果 A [1... i +1 ]的子段 A [ k .. i +1]是使得 C [ i +1 ]达到最大和的子段,那么 A [ k ... i ]一定是使得 C [ i ]达到最大和的子段.如若不然,存在一个使得 C[ i ]达到更大和的子段 A [ t ... i ],那么在 A [ t ... i ]后面加上 A[ i+1 ]所得到的子段 A [ t ... i +1]之和将大于 C [ i +1].这与 C [ i 十1]是 A [1.. i +1]以元素 A [ i +1]作为最后元素的最大子段和矛盾.这恰好验证了这样定义的优化函数满足优化原则于是,我们在考虑怎样选择才能使得 C [ i +1]达到最大值时,只要考虑一个问题:是否需要把 C [ i ]加到 A [ i +1上?而这取决于 C [ i ]是否大于0.
那么递推关系为:
若A[1]>0,否则C[1]=0
根据上面的递推公式,得到C[1],C[2],C[3].....C[n,]恰好枚举了以任何元素为最后元素的所有子段的最大和,我们要找到所求问题的最大子段和,就要对上面n个子段和进行比较,找到其中最大和。
伪代码
//MaxSum(A,n) 【动态规划】
//输入:数组A
//输出:最大子段sum,子段的最后位置c
算法分析
MaxSum(A,n) 算法只有一个for循环,执行次数为O(n),循环体内都是常数次运算,因此算法复杂度为O(n)
程序
- //算法3.10 MaxSum(A,n) 【动态规划】
- //输入:数组A
- //输出:最大子段sum,子段的最后位置c
-
- #include<stdio.h>
- #include<stdlib.h>
-
- void MaxSum(int A[], int n)
- {
- int sum = 0;
- int b = 0;
- int i,c;
- for(i = 0;i < n;i++)
- {
- if(b > 0)
- b= b+A[i];
- else
- b = A[i];
-
- if(b > sum)
- {
- sum = b;
- c = i;
- }
- }
- printf("数组A的最大连续子段和为:%d,且子段最后位置为:%d",sum,c+1);
- }
-
- int main()
- {
- int A[7]={2,-5,8,11,-3,4,6};
- int i;
- for(i = 0;i < 7;i++)
- {
- printf("%d ",A[i]);
- }
- printf("\n");
- MaxSum(A,7);
- return 0;
- }

- 1.直方图均衡化(1)什么是直方图图像直方图,是指对整个图像在灰度范围内的像素值(0~255)统计出现频率次数,据此生成的直方图,称为图像直方图-直方图。直方图反映了图像灰度的分布情况。是图像的统计学特征。(2)直方图均衡化是一种提高图像对... [详细]
赞
踩
- 写在前面最近准备尝试跑一跑TensorFlowGPU训练模型,平时开发用的MBP,无赖显卡是AMD只支持CPU训练,但恰有闲置Win10笔记本电脑一台显卡NVIDIA支持CUDA®。TensorflowGPU训练加速需要支持CUDA®的GP... [详细]
赞
踩
- 自然语言处理,建模,文本生成基于keras框架的深度学习实战,利用三国演义文本集,LSTM神经网络模型,训练文本数据,预测文本,自动生成文本。_inordertorun_eagerconst:dsttensorisnotinitialize... [详细]
赞
踩
- article
Python from import导包ModuleNotFoundError No module named,找不到模块问题_modulenotfounderror: no module named 'packaging
在学习Flask框架的蓝图时,遇到导包时用到了`from.模块import对象`,然后试了试直接import会报错,直接告诉我找不到模块,发现问题以此记录。_modulenotfounderror:nomodulenamed'packagi... [详细]赞
踩
- 1添加Druid依赖
com.alibaba druid 1.1.10 赞
踩
- 一站式掌握MacOS、IOS电脑和手机App程序设计开发,专题涵盖Objective-C、Swift语言基础、Foundation核心API、Cocoa、CocoaTouch框架以及XCode开发工具使用等内容。Cocoa-01-MacOS... [详细]
赞
踩
- 此外,Spark提供了丰富的编程接口(如Scala、Java、Python和R),可以方便地进行开发和调试。因此,Spark成为了大数据处理和分析的首选工具之一。ResilientDistributedDatasets(RDDs):RDD是... [详细]
赞
踩
- 这篇文章主要帮助大家熟悉Linux操作系统下Docker的完整安装过程,如果对Docker感兴趣的话,可以直接根据本文的步骤操作起来,如果觉得写得不错的话,请收藏起来,以备不时之需。_linux安装docker教程linux安装docker... [详细]
赞
踩
- 此方法针对安装了Dockerfor客户端Mac的用户之前上传自己封装好的docker镜像,今天去下载愣是下载了2个小时没有下载完,以为是网络的问题,换个网络还是不行。于是百度了一下需要配置镜像加速。下面记录了一下我的步骤1.注册阿里账号地址... [详细]
赞
踩
- SpringBootDruid配置详解spring:datasource:type:com.alibaba.druid.pool.DruidDataSourcedriverClassName:com.mysql.cj.jdbc.Driver... [详细]
赞
踩
- 这是「进击的Coder」的第454篇技术分享作者:小G来源:GitHubDaily“阅读本文大概需要5分钟。”在使用GitHub时,我们经常会遇到这样的问题,GitHub..._github加速下载github加速下载这是「进击的Coder... [详细]
赞
踩
- pipintall出现error:subprocess-exited-with-error错误的解决办法_subprocess-exited-with-errorsubprocess-exited-with-errorpipintall出现... [详细]
赞
踩
- 我们通常都是用Xcode生成和管理的iOSTeamProvisioningProfile来进行开发,因为它非常方便,所以不需要自己手动生成ProvisioningProfile。iOSTeamProvisioningProfile是第一次使... [详细]
赞
踩
- docker安装1、卸载docker$sudoyumremovedockerdocker-clientdocker-client-latestdocker-commondocker-latestdocker-latest-logrotate... [详细]
赞
踩
- 常见的指标有点击率CTR、转化率CVR、GMV、浏览深度和品类丰富度等。多目标建模的常用方法:-多模型的融合-多任务学习底层共享表示的优化任务序列依赖关系建模多目标建模已经成为当前推荐系统中的标配,在多目标建模过程中,需要考虑多个目标之间的... [详细]
赞
踩
- 随着时代的进步,OLED显示屏成为了继LCD显示屏之后的新一代显示屏技术,OLED具有可视角高,功耗低,厚度薄,耐冲击、振动能力强,像素响应时间低等优点,在嵌入式开发中,OLED显示器也是一个主要的部分,制作OLED显示模块的驱动也是学习S... [详细]
赞
踩
- 老机器摇身一变成局域网下低配服务器,并稳定访问GitHub_腾讯云服务github腾讯云服务github老机器摇身一变成局域网下低配服务器,并稳定访问GitHub搭建场景:问题背景:最近用腾讯云服务器访问GitHub经常挂,试了很多解决方案... [详细]
赞
踩
- 我真的受不了虚拟机了,我电脑上有9个虚拟机,占了132G!!!我还不敢随便删,怕到时候要用。。。所以,我要学习一下docker,拯救一下我的硬盘!!!_配置docker镜像家属器配置docker镜像家属器文章目录前言一、准备工作二、dock... [详细]
赞
踩
- article
iOS 如何将证书和描述文件给其他人进行真机调试(Provisioning profile "描述文件的名字" doesn't include the currently selected devic...
1.去钥匙串中将证书以.p12的格式导出(导出的时候最好设置密码,安全)。2.去开发者中心,将真机的UUID加入到账号中。如图3.进入描述文件所在的位置,选中所需的描述文件,点edit进入编辑状态,选中刚才添加的手机也就是UUID,点击co... [详细]赞
踩
- 攻击路径是指网络攻击者潜入到企业内部网络应用系统所采取的路径,换句话说,也就是攻击者进行攻击时所采取的相关措施。攻击途径通常代表着有明确目的性的威胁,因为它们会经过详细的准备和规划。从心怀不满的内部人员到恶意黑客、间谍团伙,都可能会利用这些... [详细]
赞
踩



