devbox
代码独立开发者
这个屌丝很懒，什么也没留下！
关注作者
热门标签
热门文章
当前位置:   article > 正文

2019年第十届蓝桥杯B组决赛_第十届蓝桥杯决赛b组

作者：代码独立开发者 | 2024-01-30 19:18:17

赞

踩

第十届蓝桥杯决赛b组

一.平方末尾

题目描述

本题为填空题，只需要算出结果后，在代码中使用输出语句将所填结果输出即可。

能够表示为某个整数的平方的数字称为“平方数”

虽然无法立即说出某个数是平方数，但经常可以断定某个数不是平方数。 因为平方数的末位只可能是：[0,1,4,5,6,9] 这 66 个数字中的某个。 所以，4325435332 必然不是平方数。

如果给你一个 2 位或 2 位以上的数字，你能根据末位的两位来断定它不是平方数吗？

请计算一下，一个 2 位以上的平方数的最后两位有多少种可能性？

运行限制

  • 最大运行时间：1s
  • 最大运行内存: 128M

思路：我们只需要两位数生成平方数的最后两位的所有情况，再根据题意进行判断即可。

当超过两位数的时候，由于高于两位数的数位并不会对最后两位的值产生影响，因此只需要枚举0-99即可。（当然由于10*10 = 100，100%100=0，因此本程序已经在10的时候包含了00）

例如：123 * 456，当1与456中的数位做乘法的时候，就算是对于个位6，乘法后的数位会在百位上，并不会影响到个位和十位。

  1. #include <bits/stdc++.h>
  2. using namespace std;
  3. int main()
  4. {
  5.   int i, j;
  6.   set<int> number;
  7.   for(i = 10; i < 100; ++ i)
  8.   {
  9.     j = i * i;
  10.     number.insert(j % 100);
  11.   }
  12.   cout << number.size();
  13.   return 0;
  14. }

二.质数拆分

题目描述

本题为填空题，只需要算出结果后，在代码中使用输出语句将所填结果输出即可。

将 2019 拆分为若干个两两不同的质数之和，一共有多少种不同的方法？

注意交换顺序视为同一种方法，例如 2 + 2017 = 2019 与 2017 + 2 = 2019 视为同一种方法。

运行限制

  • 最大运行时间：1s
  • 最大运行内存: 128M

思路：注意本题说的两两不同并不是说只能由两个数组成。

dp[i]定义为组成i的方案数，初始化dp[0]=1，这是因为2019不是质数，因此需要组合出2019，至少需要两个质数。

本题就是一个变种的0-1背包问题，dp[i]记录的是组合方案数。

  1. #include <iostream>
  2. #include <cstring>
  3. using namespace std;
  4.  
  5. bool notPrime[2020];
  6. int primes[2020], cnt;
  7. const int n = 2019;
  8.  
  9. void euler(int num)
  10. {
  11.   int i, j;
  12.   for(i = 2; i <= num; ++ i)
  13.   {
  14.     if(!notPrime[i])
  15.     {
  16.       primes[cnt ++] = i;
  17.     }
  18.     for(j = 0; j < cnt && primes[j] * i <= num; ++ j)
  19.     {
  20.       notPrime[primes[j] * i] = true;
  21.       if(i % primes[j] == 0)
  22.       {
  23.         break;
  24.       }
  25.     }
  26.   }
  27. }
  28.  
  29. int main()
  30. {
  31.   long long dp[2020], i, j;
  32.   memset(dp, 0, sizeof(dp));
  33.   dp[0] = 1;
  34.   euler(n);
  35.   for(i = 0; i < cnt; ++ i)
  36.   {
  37.     for(j = n; j >= primes[i]; -- j)
  38.     {
  39.       dp[j] += dp[j - primes[i]];
  40.     }
  41.   }
  42.   cout << dp[n];
  43.   return 0;
  44. }

三.拼接

题目描述

本题为填空题，只需要算出结果后，在代码中使用输出语句将所填结果输出即可。

小明要把一根木头切成两段，然后拼接成一个直角。

如下图所示，他把中间部分分成了 n×n 的小正方形，他标记了每个小正方形属于左边还是右边。然后沿两边的分界线将木头切断，将右边旋转向上后拼 接在一起。

图片描述

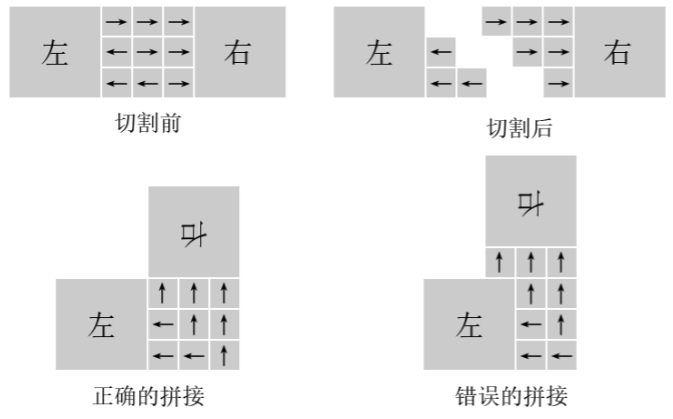
要求每个小正方形都正好属于左边或右边，而且同一边的必须是连通的。在拼接时，拼接的部位必须保持在原来大正方形里面。

请问，对于 7×7 的小正方形，有多少种合法的划分小正方形的方式。

运行限制

  • 最大运行时间：1s
  • 最大运行内存: 128M

思路：可以发现，只需要切分前后，两个部分的方块都是关于反对角线对称的即可。拼接的方案就是把右边部分向上翻折即可。因此本题问的就是有什么方法保证切割后左右两部分要么没有，要么是关于反对角线对称的。实际上我们可以以反对角线经过的格点为起点，遍历上面的部分，注意不要越过反对角线，当遍历到边界的时候，对称到下面部分，就可以将图形分开为两个满足条件的部分。

  1. #include <iostream>
  2. using namespace std;
  3. const int n = 7;
  4. bool visited[n + 5][n + 5];
  5.  
  6. void DFS(int x, int y, int& ans)
  7. {
  8.   if(!x || x == n || !y || y == n)
  9.   {
  10.     ++ ans;
  11.     return;
  12.   }
  13.   //向上走 不可能越过反对角线
  14.   if(x > 0 && !visited[x - 1][y])
  15.   {
  16.     visited[x - 1][y] = true;
  17.     DFS(x - 1, y, ans);
  18.     visited[x - 1][y] = false;
  19.   }
  20.   //向左走 不可能越过反对角线
  21.   if(y > 0 && !visited[x][y - 1])
  22.   {
  23.     visited[x][y - 1] = true;
  24.     DFS(x, y - 1, ans);
  25.     visited[x][y- 1] = false;
  26.   }
  27.   //向下走 且 不越过反对角线
  28.   if(x < n && x + 1 + y < n && !visited[x + 1][y])
  29.   {
  30.     visited[x + 1][y] = true;
  31.     DFS(x + 1, y, ans);
  32.     visited[x + 1][y] = false;
  33.   }
  34.   //向右走 且 不越过反对角线
  35.   if(y < n && x + y + 1 < n && !visited[x][y + 1])
  36.   {
  37.     visited[x][y + 1] = true;
  38.     DFS(x, y + 1, ans);
  39.     visited[x][y + 1] = false;
  40.   }
  41. }
  42.  
  43. int main()
  44. {
  45.   int sx = n, sy = 0, ans;
  46.   while(sx >= 0 && sy <= n)
  47.   {
  48.     visited[sx][sy] = true;
  49.     DFS(sx, sy, ans);
  50.     visited[sx][sy] = false;
  51.     -- sx;
  52.     ++ sy;
  53.   }
  54.   cout << ans;
  55.   return 0;
  56. }

四.求值

题目描述

本题为填空题，只需要算出结果后，在代码中使用输出语句将所填结果输出即可。

学习了约数后，小明对于约数很好奇，他发现，给定一个正整数 t，总是可以找到含有 t 个约数的整数。小明对于含有 t 个约数的最小数非常感兴趣，并把它定义为
例如 S1​ = 1, S2​ = 2, S3​ = 4, S4​ = 6，· · ·。 现在小明想知道，当 t = 100 时，St​是多少？即 S100​是多少？

思路：本题是填空题，直接暴力解就可以啦，暴力解结果再填空就行。

  1. #include <iostream>
  2. using namespace std;
  3. typedef long long LL;
  4.  
  5. int main()
  6. {
  7. 	LL num, fac;
  8. 	int factor_num;
  9. 	for(num = 1; ; ++ num)
  10. 	{
  11. 		factor_num = 0;
  12. 		for(fac = 1; fac * fac <= num; ++ fac)
  13. 		{
  14. 			if(num % fac == 0)
  15. 			{
  16. 				if(num == fac * fac)
  17. 				{
  18. 					++ factor_num;
  19. 				}
  20. 				else
  21. 				{
  22. 					factor_num = factor_num + 2;
  23. 				}
  24. 			}
  25. 		}
  26. 		if(factor_num == 100)
  27. 		{
  28. 			cout << num;
  29. 			break;
  30. 		}
  31. 	}
  32. }

五.路径计数

题目描述

本题为填空题，只需要算出结果后，在代码中使用输出语句将所填结果输出即可。

从一个 5×5 的方格矩阵的左上角出发，沿着方格的边走，满足以下条件的路线有多少种？

  1. 总长度不超过 12；
  2. 最后回到左上角；
  3. 路线不自交；
  4. 不走出 5×5 的方格矩阵范围之外。 如下图所示ABC 是三种合法的路线。注意 B 和 C 由于方向不同，所以 视为不同的路线。

图片描述

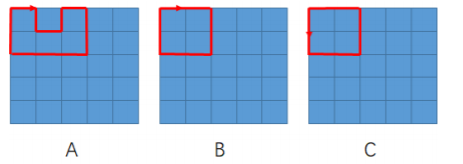
运行限制

  • 最大运行时间：1s
  • 最大运行内存: 128M

思路：DFS，本题要求最后回到出发点，且路径长度<=12，对格点进行DFS即可。需要注意的是，我们只要要求路径长度>2，就可以防止路径出去就回来：

  1. #include <iostream>
  2. using namespace std;
  3. const int n = 5;
  4.  
  5. bool visited[n + 5][n + 5];
  6. int ans, dir[4][2] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
  7.  
  8. bool check(int x, int y)
  9. {
  10.   return x >= 0 && x < n && y >= 0 && y < n;
  11. }
  12.  
  13. void DFS(int x, int y, int path_len)
  14. {
  15.   if(path_len > 12)
  16.   {
  17.     return;
  18.   }
  19.   //最后回到了出发点0,0
  20.   if(!x && !y && path_len > 2)
  21.   {
  22.     ++ ans;
  23.     return;
  24.   }
  25.   for(int i = 0; i < 4; ++ i)
  26.   {
  27.     int nx = dir[i][0] + x;
  28.     int ny = dir[i][1] + y;
  29.     if(check(nx, ny) && !visited[nx][ny])
  30.     {
  31.       visited[nx][ny] = true;
  32.       DFS(nx, ny, path_len + 1);
  33.       visited[nx][ny] = false;
  34.     }
  35.   }
  36. }
  37.  
  38. int main()
  39. {
  40.   DFS(0, 0, 0);
  41.   cout << ans;
  42.   return 0;
  43. }

注：本题的标准答案排除了走到边界点(0,5)和(5,0)的情况，包括他们的正向和逆向，共4种。但实际上他们的路径长度都为12，是满足题意的，有争议。

六.最优包含

题目描述

我们称一个字符串 S 包含字符串 T 是指 T 是 S 的一个子序列，即可以从字符串 S 中抽出若干个字符，它们按原来的顺序组合成一个新的字符串与 T 完全一样。

给定两个字符串 S 和 T，请问最少修改 S 中的多少个字符，能使 S 包含 T ？

其中，1≤∣T∣≤∣S∣≤1000。

输入描述

输入两行，每行一个字符串。

第一行的字符串为 S，第二行的字符串为 T。

两个字符串均非空而且只包含大写英文字母。

输出描述

输出一个整数，表示答案。

输入输出样例

示例

输入

  1. ABCDEABCD
  2. XAABZ

输出

3

运行限制

  • 最大运行时间：1s
  • 最大运行内存: 256M

思路：本题的题意就是要求最少修改S串中的字符，使得T是S的子序列。

我们定义dp[i][j]表示S[1~i]包含T[1~j]：

A.假如当前要考虑的是dp[i][j]，那么如果S[i]=T[j]，显然dp[i][j]=dp[i-1][j-1]。

B.否则，我们可以选择：dp[i][j]=min(dp[i-1][j-1]+1,dp[i-1][j])。

  1.将S[i]改变为T[j]，此时步数为dp[i-1][j-1]+1

  2.让S[1~i-1]包含T[1~j]，此时步数为dp[i-1][j]

值得注意的是：

1.dp[i][0]=0(0<=i<=n)，因为空串是任意长度的串的子序列。

2.对于dp[i][j](i<j)是非法的，但是由于状态转移的时候，dp[i][j]=min(dp[i-1][j-1]+1,dp[i][j]=dp[i-1][j])是取min的，因此我们可以初始化为一个很大的数，利用取min的性质，就可以用大数表示非法状态，进而在取min的时候直接舍弃。

  1. #include <iostream>
  2. #include <string>
  3. #include <cstring>
  4. using namespace std;
  5.  
  6. const int MaxN = 1005;
  7.  
  8. int dp[MaxN][MaxN];
  9. char S[MaxN] ,T[MaxN];
  10.  
  11. int main()
  12. {
  13.   cin >> S + 1 >> T + 1;
  14.   int i, j, n = strlen(S + 1), m = strlen(T + 1);  
  15.   memset(dp, 0x3f3f, sizeof(dp));
  16.   dp[0][0] = 0;
  17.   for(i = 1; i <= n; ++ i)
  18.   {
  19.     dp[i][0] = 0;
  20.     for(j = 1; j <= m && j <= i; ++ j)
  21.     {
  22.       if(S[i] == T[j])
  23.       {
  24.         dp[i][j] = dp[i - 1][j - 1];
  25.       }
  26.       else // 可以选择修改 S[i] = T[j]，修改数量为dp[i - 1][j - 1] + 1; 也可以选择让S[1~i-1]包含T[1~j]
  27.       {
  28.         dp[i][j] = min(dp[i - 1][j - 1] + 1, dp[i - 1][j]);
  29.       }
  30.     }
  31.   }
  32.   cout << dp[n][m];
  33.   return 0;
  34. }

七.排列数

题目描述

在一个排列中，一个折点是指排列中的一个元素，它同时小于两边的元素，或者同时大于两边的元素。对于一个 1 ∼ n 的排列，如果可以将这个排列中包含 t 个折点，则它称为一个 t+1 单调序列。

例如，排列 (1,4,2,3) 是一个 3 单调序列，其中 4 和 2 都是折点。

给定 n 和 k，请问 1 ∼ n 的所有排列中有多少个 k 单调队列？

输入描述

输入一行包含两个整数 n,k (1≤k≤n≤500)。

输出描述

输出一个整数，表示答案。答案可能很大，你可需要输出满足条件的排列数量除以 123456 的余数即可。

输入输出样例

示例

输入

4 2

输出

12

运行限制

  • 最大运行时间：3s
  • 最大运行内存: 256M

思路：本题很直观的想法就是直接生成排列再按照条件进行统计。但是1~500的全排列还是比较容易超时的，当然我们也可以看k到底是接近1还是500，从而选择是从1~500开始用next_permutation还是从500~1开始用prev_permutation。但这都不是很好的想法，实际上思考排列，我们会发现，从1~n-1的排列得到1~n的排列只需要选择n放置在1~n-1的排列中的n个空位置中的某一个就可以了。大规模的排列是可以从小规模的排列推得的，我们可以尝试构想一下 从 1~i-1的排列，k-1个拐点 得到 1~i的排列，k个拐点的 迁移方式。

定义dp[i][k]表示1~i的排列中 拐点数量为k个的个数。

1.很显然，当i=1时，只有dp[i][0]=1是合法的，其余均非法。

2.当i=2时，只有dp[i][0]=2是合法的(从大到小与从小到大)，其余均非法。(构成拐点至少3个点)

3.当i>2时，一切都玄乎了起来（雾）：需要谨记我们考虑的i是当前考虑的数中最大的数

假设当前状态为dp[i][j]

A.i放置在当前已生成排列的左右两端

  (1)拐点数量为偶数个  j为偶数

    a.先波峰再波谷

由图很容易知道，这样做会在左端或者右端产生一个波谷（不可能是波峰是因为i是当前的最大值，而i在最边上，所以i不可能是拐点，而其他点都比他小，因此只能产生一个波谷）。

产生波谷：dp[i+1][j+1] = dp[i+1][j+1] + dp[i][j] / 2

不产生波谷：dp[i+1][j] = dp[i+1][j] + dp[i][j] / 2

注：dp[i][j]包含了先波峰后波谷与先波谷后波峰两种情况，且两种情况各占dp[i][j]的一半

    b.先波谷后波峰

这种情况会在右端产生一个波谷，读者可以自行画图看看。

产生波谷：dp[i+1][j+1] = dp[i+1][j+1] + dp[i][j] / 2

不产生波谷：dp[i+1][j] = dp[i+1][j] + dp[i][j] / 2

综上，当j为偶数时

dp[i+1][j+1] = dp[i+1][j+1] + dp[i][j]

dp[i+1][j] = dp[i+1][j] + dp[i][j]

  (2)拐点数量为奇数个  j为奇数

    a.先波峰后波谷

由图很容易知道，这样做会在左端或右端都会产生一个波谷

产生波谷：dp[i+1][j+1] = dp[i+1][j+1] + dp[i][j] / 2 * 2

dp[i][j] / 2:先波峰后波谷的情况占了dp[i][j]的一半

*2:这一半的情况中，左右两个端点都可以增加一个波谷

  b.先波谷后波峰

读者可以画图看，我们这里直接证：由于是先波谷，因此有A[1]>A[2]，此时我们让A[0]=i，就有A[0]>A[1]>A[2]，并不会产生新的波峰或波谷。

同理，由于有奇数个拐点，因此A[i-2]与A[i-1]的关系可以推知是A[i-2]<A[i-1](不理解可以画图看)，此时我们让A[i]=i，就有A[i-2]<A[i-1]<A[i]，也不会产生新的波峰或波谷。

不产生波谷：dp[i+1][j] = dp[i+1][j] + dp[i][j]

综上，在奇数情况下，先峰后谷会产生两个波谷，先谷后峰不产生新的波峰或波谷，因此：

综上，当j为奇数时

产生波谷：dp[i+1][j+1] = dp[i+1][j+1] + dp[i][j]

不产生波谷：dp[i+1][j] = dp[i+1][j] + dp[i][j]

综合奇偶情况来看，无需考虑j的奇偶性质，均有

dp[i+1][j+1] = dp[i+1][j+1] + dp[i][j]

dp[i+1][j] = dp[i+1][j] + dp[i][j]

B.i放置在当前已生成排列的中间

  (1)放置在波峰两端

如图，只会有一个新波峰代替旧波峰，并不会增加或减少拐点数量。即：

dp[i+1][j] = dp[i+1][j] + dp[i][j] *  (波峰数量 * 2)；

*2:在波峰的左右两边放置都只是将原波峰变高，不会产生新的波峰

  (2)放置在波谷两端

如图，这种情况下，会产生一个新的波峰与波谷。 

    (3)放置在波峰与波谷中间

如图，这种情况下，会产生一个新的波峰与波谷。

综合(2)、(3)我们可以发现，只要不放置在波峰两边和两个端点处，其余地方放置都会产生两个新拐点，即：

dp[i+1][j+2] = dp[i+1][j+2] + dp[i][j] *  (i - 1 - 波峰数量 * 2)；

i - 1:i个点构成i-1端，i - 1个端上可有i-1种放置i的情形

i - 1 - 波峰数量 * 2:i - 1种情形减去波峰左右两种情形【需要明确的是图形必定是波峰波谷交替，因此也不会存在重复减去的情况，因为不可能两个波峰之间有相同的相邻点】

有了上面的知识我们再来做一次梳理，可以明确的是，当增加一个点之后，最多增加两个拐点：

A.偶数个拐点，先谷后峰

不增加拐点： j / 2 * 2 + 1，方案数为(乘法原理)：dp[i+1][j] += dp[i][j]*(j/2*2+1)=dp[i][j]*(j+1)

j / 2：波峰数量        *2：波峰左右       +1：最左边

增加一个拐点：2，总方案数为：dp[i+1][j+1] += dp[i][j]*2

增加两个拐点：i + 1 - 2 - (j / 2 * 2 + 1)

i + 1：i个数有i+1个空位，用容斥原理可得增加两个拐点的方案数量

B.偶数个拐点，先峰后谷

不增加拐点： j / 2 * 2 + 1，方案数为(乘法原理)：dp[i+1][j] += dp[i][j]*(j/2*2+1)=dp[i][j]*(j+1)

j / 2：波峰数量        *2：波峰左右       +1：最右边

增加一个拐点：2，总方案数为：dp[i+1][j+1] += dp[i][j]*2

增加两个拐点：i + 1 - 2 - (j / 2 * 2 + 1)

i + 1：i个数有i+1个空位，用容斥原理可得增加两个拐点的方案数量

C.奇数个拐点，先谷后峰

不增加拐点： (j - 1) / 2 * 2 + 2，方案数为(乘法原理)：dp[i+1][j] += dp[i][j]*(j/2*2+1)=dp[i][j]*(j+1)

(j - 1) / 2：波峰数量        *2：波峰左右       +2：最左边和最右边

增加一个拐点：2，总方案数为：dp[i+1][j+1] += dp[i][j]*2

增加两个拐点：i + 1 - 2 - (j / 2 * 2 + 1)

i + 1：i个数有i+1个空位，用容斥原理可得增加两个拐点的方案数量

D.奇数个拐点，先峰后谷

不增加拐点： (j + 1) / 2 * 2，方案数为(乘法原理)：dp[i+1][j] += dp[i][j]*(j/2*2+1)=dp[i][j]*(j+1)

(j + 1) / 2：波峰数量        *2：波峰左右

增加一个拐点：2，总方案数为：dp[i+1][j+1] += dp[i][j]*2

增加两个拐点：i + 1 - (2) - (j / 2 * 2 + 1)

i + 1：i个数有i+1个空位，用容斥原理可得增加两个拐点的方案数量

于是！！！我们会惊讶地发现，这四种情况下，拐点增加的三种情形的公式居然一毛一样，ORZ

整理递推式：

dp[i+1][j] = dp[i+1][j] + dp[i][j]*(j+1)

dp[i+1][j+1] = dp[i+1][j+1] + dp[i][j]*2

dp[i+1][j+2] = dp[i+1][j+2] + dp[i][j]*(i-j-2)

  1. #include <iostream>
  2. using namespace std;
  3. const int mod = 123456;
  4.  
  5. int dp[505][505];
  6.  
  7. int main()
  8. {
  9.   int n, k, i, j;
  10.   cin >> n >> k;
  11.   dp[1][0] = 1;
  12.   for(i = 2; i <= n; ++ i)
  13.   {
  14.     dp[i][0] = 2;
  15.     for(j = 0; j <= i - 2; ++ j)
  16.     {
  17.       dp[i + 1][j] = (dp[i + 1][j] + dp[i][j] * (j + 1) % mod) % mod;
  18.       dp[i + 1][j + 1] = (dp[i + 1][j + 1] + dp[i][j] * 2 % mod) % mod;
  19.       dp[i + 1][j + 2] = (dp[i + 1][j + 2] + dp[i][j] * (i - j - 2) % mod) % mod; 
  20.     }
  21.   }
  22.   cout << dp[n][k - 1];
  23.   return 0;
  24. }

八.解谜游戏

题目描述

小明正在玩一款解谜游戏。谜题由 24 根塑料棒组成，其中黄色塑料棒 4 根，红色 8 根，绿色 12 根 (后面用 Y 表示黄色、R 表示红色、G 表示绿色)。初始时这些塑料棒排成三圈，如上图所示，外圈 12 根，中圈 8 根，内圈 4 根。

小明可以进行三种操作：

  1. 将三圈塑料棒都顺时针旋转一个单位。例如当前外圈从 0 点位置开始顺时针依次是 YRYGRYGRGGGG，中圈是 RGRGGRRY，内圈是 GGGR。那么顺时针旋转一次之后，外圈、中圈、内圈依次变为：GYRYGRYGRGGG、 YRGRGGRR 和 RGGG。

  2. 将三圈塑料棒都逆时针旋转一个单位。例如当前外圈从 0 点位置开始顺时针依次是 YRYGRYGRGGGG，中圈是 RGRGGRRY，内圈是 GGGR。那么逆时针旋转一次之后，外圈、中圈、内圈依次变为：RYGRYGRGGGGY、 GRGGRRYR 和 GGRG。

  3. 将三圈 0 点位置的塑料棒做一个轮换。具体来说：外圈 0 点塑料棒移动到内圈 0 点，内圈 0 点移动到中圈 0 点，中圈 0 点移动到外圈 0 点。例如当前外圈从 0 点位置开始顺时针依次是 YRYGRYGRGGGG，中圈是 RGRGGRRY，内圈是 GGGR。那么轮换一次之后，外圈、中圈、内圈依次变为：RRYGRYGRGGGG、GGRGGRRY 和 YGGR。

小明的目标是把所有绿色移动到外圈、所有红色移动中圈、所有黄色移动到内圈。给定初始状态，请你判断小明是否可以达成目标？

输入描述

第一行包含一个整数 T (1≤T≤100)，代表询问的组数。

每组询问包含 3 行：

第一行包含 12 个大写字母，代表外圈从 0 点位置开始顺时针每个塑料棒的颜色。

第二行包含 8 个大写字母，代表中圈从 0 点位置开始顺时针每个塑料棒的颜色。

第三行包含 4 个大写字母，代表内圈从 0 点位置开始顺时针每个塑料棒的颜色。

输出描述

对于每组询问，输出一行 YES 或者 NO，代表小明是否可以达成目标。

输入输出样例

示例

输入

  1. 2
  2. GYGGGGGGGGGG
  3. RGRRRRRR
  4. YRYY
  5. YGGGRRRRGGGY
  6. YGGGRRRR
  7. YGGG

输出

  1. YES
  2. NO

运行限制

  • 最大运行时间：1s
  • 最大运行内存: 256M

思路：本题比较容易想到的思路是BFS，但是这道题的可转移状态实在是太多了，BFS并不是一个很好的解法。实际上，我们观察外中内三个圈，他们的数量分别为12、8、4，我们先做个标记：

我们关注最内层的4根，每次要交换时最多只有4种被换出去的情况，同理，中层与其他层发生交换时，最多只有8种被换出去的情况，类推至外层。

于是我们发现可以交换的塑料棒是按组分的，不同组之间是不可以跨越的。

组0组1组2组3
内0123
中0，41，52，63，7
外0，4，81，5，92，6，103，7，11

于是我们可以发现，实际上 编号%4 相同的是处于同一组的。

[值得注意的是，每次交换时，是内中外三层中的同一组，组内各出一个元素进行轮换]

然而我们发现，三个发生交换的组，虽然要求的交换方式是：

外圈 0 点塑料棒移动到内圈 0 点，内圈 0 点移动到中圈 0 点，中圈 0 点移动到外圈 0 点

0点可以通过旋转将同组的点转到0点

似乎交换顺序只能是 外->内->中->外，但是实际上，由于中圈和外圈的组内元素数量>1，因此是可以做到随机交换的。此时我们只需要判断，每一个组里，G、R、Y的分量是否都是总量的1/4就可以了。

  1. #include <iostream>
  2. #include <string>
  3. #include <cstring>
  4. using namespace std;
  5.  
  6. int countG[4], countR[4], countY[4];
  7.  
  8. void countColorNum(string colorSerial)
  9. {
  10.   for(int i = colorSerial.size() - 1; i >= 0; -- i)
  11.   {
  12.     switch(colorSerial[i])
  13.     {
  14.       case 'G':
  15.               ++ countG[i % 4];
  16.               break;
  17.       case 'R':
  18.               ++ countR[i % 4];
  19.               break;
  20.       case 'Y':
  21.               ++ countY[i % 4];
  22.               break;
  23.     }
  24.   }
  25. }
  26.  
  27. int main()
  28. {
  29.   int T;
  30.   cin >> T;
  31.   string stringG, stringR, stringY;
  32.   while(cin >> stringG >> stringR >> stringY)
  33.   {
  34.     memset(countG, 0, sizeof(countG));
  35.     memset(countR, 0, sizeof(countR));
  36.     memset(countY, 0, sizeof(countY));
  37.     countColorNum(stringG);
  38.     countColorNum(stringR);
  39.     countColorNum(stringY);
  40.     for(int i = 0; i < 4; ++ i)
  41.     {
  42.       if(countG[i] != 3 || countR[i] != 2 || countY[i] != 1)
  43.       {
  44.         cout << "NO" << endl;
  45.         break;
  46.       }
  47.       if(i == 3)
  48.       {
  49.         cout << "YES" << endl;
  50.       }
  51.     }
  52.   }
  53.   return 0;
  54. }

九.第八大奇迹

题目描述

在一条 R 河流域，繁衍着一个古老的名族 Z。他们世代沿河而居，也在河边发展出了璀璨的文明。

Z 族在 R 河沿岸修建了很多建筑，最近，他们热衷攀比起来。他们总是在比谁的建筑建得最奇特。

幸好 Z 族人对奇特的理解都差不多，他们很快给每栋建筑都打了分，这样评选谁最奇特就轻而易举了。

于是，根据分值，大家很快评出了最奇特的建筑，称为大奇迹。

后来他们又陆续评选了第二奇特、第二奇特、......、第七奇特的建筑，依次称为第二大奇迹、第三大奇迹、......、第七大奇迹。

最近，他们开始评选第八奇特的建筑，准备命名为第八大奇迹。

在评选中，他们遇到了一些问题。

首先，Z 族一直在发展，有的建筑被拆除又建了新的建筑，新建筑的奇特值和原建筑不一样，这使得评选不那么容易了。

其次，Z 族的每个人所生活的范围可能不一样，他们见过的建筑并不是所有的建筑，他们坚持他们自己所看到的第八奇特的建筑就是第八大奇迹。

Z 族首领最近很头疼这个问题，他害怕因为意见不一致导致 Z 族发生分歧。他找到你，他想先了解一下，民众自己认为的奇迹是怎样的。

现在告诉在 R 河周边的建筑的变化情况，以及在变化过程中一些人的生活范围，请编程求出每个人认为的第八大奇迹的奇特值是多少。

输入描述

输入的第一行包含两个整数 L,N，分别表示河流的长度和要你处理的信息的数量。开始时河流沿岸没有建筑，或者说所有的奇特值为 0。

接下来 N 行，每行一条你要处理的信息。

如果信息为 C p x，表示流域中第 p (1≤p≤L) 个位置建立了一个建筑，其奇特值为 x。如果这个位置原来有建筑，原来的建筑会被拆除。

如果信息为 Q a b，表示有个人生活的范围是河流的第 a 到 b 个位置（包含 a 和 b，a≤b），这时你要算出这个区间的第八大奇迹的奇特值，并输出。如果找不到第八大奇迹，输出 0。

其中，1≤L≤10^5，1≤N≤10^5。所有奇特值为不超过10^9的非负整数。

输出描述

对于每个为 Q 的信息，你需要输出一个整数，表示区间中第八大奇迹的奇特值。

输入输出样例

示例

输入

  1. 10 15
  2. C 1 10
  3. C 2 20
  4. C 3 30
  5. C 4 40
  6. C 5 50
  7. C 6 60
  8. C 7 70
  9. C 8 80
  10. C 9 90
  11. C 10 100
  12. Q 1 2
  13. Q 1 10
  14. Q 1 8
  15. C 10 1
  16. Q 1 10

输出

  1. 0
  2. 30

运行限制

  • 最大运行时间：1s
  • 最大运行内存: 256M

十.燃烧权杖

题目描述

小 C 最近迷上了一款游戏。现在，在游戏中，小 C 有一个英雄，生命值为 x；敌人也有一个英雄，生命值为 y。除此以外，还有 kk 个士兵，生命值分别为 a1​、a2​、......、ak​。

现在小 C 打算使用一个叫做"燃烧权杖"的技能。"燃烧权杖"会每次等概率随机选择一个活着的角色（英雄或士兵），扣减其 10 点生命值，然后如果该角色的生命值小于或等于 0，则该角色死亡，不会再被"燃烧权杖"选中。"燃烧权杖"会重复做上述操作，直至任意一名英雄死亡。

小 C 想知道使用"燃烧权杖"后敌方英雄死亡（即，小 C 的英雄存活）的概率。为了避免精度误差，你只需要输出答案模一个质数 p 的结果，具体见输出描述。

输入描述

输入包含多组数据。

输入第一行包含一个正整数 T，表示数据组数。

接下来 TT 组，每组数据第一行包含四个非负整数 x、y、p、k，分别表示小 C 的英雄的生命值、敌方英雄的生命值，模数和士兵个数。 第二行包含 k 个正整数 a1​、a2​、......、ak​，分别表示每个士兵的生命值。

输出描述

对于每组数据，输出一行一个非负整数，表示答案模质数 p 的余数。

可以证明，答案一定为有理数。设答案为 a/b（a 和 b 为互质的正整数），你输出的数为 x，则你需要保证 a 与 bx 模 p同余；也即，x=(a*b^{-1})\ mod\ p， 其中 b^{-1} 表示 b 模 p 的逆元， mod 为取模运算。

输入输出样例

示例

输入

  1. 6
  2. 1 10 101 0
  3. 100 1 101 0
  4. 50 30 4903 2
  5. 1 1
  6. 987 654 233 1
  7. 321
  8. 1000000000 9999999999 233 3
  9. 1 2 3
  10. 1000000000 999999999 3 3
  11. 1 2 3

输出

  1. 51
  2. 37
  3. 1035
  4. 118
  5. 117
  6. 2

运行限制

  • 最大运行时间：1s
  • 最大运行内存: 256M

思路：首先需要明确的是，本题的胜负条件为两个英雄中任意一位死亡，和士兵是没有关系的，因此本题的士兵为干扰信息，考虑士兵只会让题目更加复杂。

根据英雄血量，我们可以算出，x最多被烧n=x/10+(x%10!=0)次，y最多被烧m=y/10+(y%10!=0)次，要想让x或者，我们可以列出下列几种情况[有点像伯努利分布，第i次结束实验]。对于x和y，每次烧其中一个人的概率是1/2：

第几次结束mm+1...m+n-1
发生概率C_{m-1}^{m-1}*\frac{1}{2^{m-1}}*\frac{1}{2}=C_{m-1}^{m-1}*\frac{1}{2^m}C_{m}^{m-1}*\frac{1}{2^{m+1}}...C_{m+n-2}^{m-1}*\frac{1}{2^{m+n-1}}

本题的m、n范围可能很大，求阶乘是不太现实的。需要注意质数p的条件，其实这在暗示我们使用卢卡斯定理进行分解：https://blog.csdn.net/qq_39304630/article/details/77417017

  1. #include <iostream>
  2. using namespace std;
  3. typedef long long ll;
  4.  
  5. ll quickMul(ll A,ll B,ll P)
  6. {
  7. 	ll res = 1;
  8. 	while(B)
  9.   {
  10. 		if(B & 1){
  11. 			res = res * A % P;
  12. 		}
  13. 		B >>= 1;
  14. 		A = A * A % P;
  15. 	}
  16. 	return res;
  17. }
  18.  
  19. ll inv(ll n,ll p) // 费马小定理求解逆元  n^(p-1)=1(mod p)  前提是 n 与 p 互质
  20. {
  21.   return quickMul(n, p-2, p);
  22. }
  23.  
  24. ll C(ll n,ll r,ll p){
  25.   if(r > n) return 0;
  26. 	ll res = 1;
  27. 	for(ll i = 1; i <= r; ++ i, -- n)
  28.   {
  29. 		res =  res * n % p * inv(i, p) % p;
  30. 	}
  31. 	return res;
  32. }
  33.  
  34. ll Lucas(ll n,ll r,ll p)
  35. {
  36. 	return r == 0 ? 1 : Lucas(n/p, r/p, p) * C (n%p, r%p, p) % p; 
  37. }
  38.  
  39. int main()
  40. {
  41.   ios::sync_with_stdio(false);
  42.   cin.tie(0) , cout.tie(0);
  43.   ll T, x, y, p, k, n, m, buttom, inv_2, ans;
  44.   cin >> T;
  45.   while(T --)
  46.   {
  47.     cin >> x >> y >> p >> k;
  48.     n = x / 10 + (x % 10 != 0);
  49.     m = y / 10 + (y % 10 != 0);
  50.     while(k --)
  51.     {
  52.       cin >> inv_2;
  53.     }
  54.     inv_2 = inv(2, p);
  55.     ans = 0;
  56.     for(buttom = m; buttom <= m + n - 1; ++ buttom)
  57.     {
  58.       ans = (ans + Lucas(buttom - 1, m - 1, p) * quickMul(inv_2, buttom, p)) % p;
  59.     }
  60.     cout << ans << endl;
  61.   }
  62.   return 0;
  63. }

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/blog/article/detail/48399
推荐阅读
相关标签

Copyright © 2003-2013 www.wpsshop.cn 版权所有，并保留所有权利。

  

闽ICP备14008679号