【数图大作业】基于模板匹配的文字识别（二）（文字行列分割）_模板分割和识别

【数图大作业】基于模板匹配的文字识别（一）
上一篇简要介绍了题目要求，并给出了实现要点和预处理部分实现方案。
下面进行行列分割部分的介绍。之所以需要进行行列分割，是因为我们的测试图像是包含多个汉字（或许还有空格和标点符号）的图片，如果直接进行模板匹配，无法确定待匹配对象。所以为了截取 ROI ，我们在对测试图像进行预处理之后，要对文字进行行列分割。

行分割

任务：

确定每行文字的开始行和结束行的位置。

步骤：

先将源图像进行二值化反色得到黑底白字的反色图，从反色图像第一行开始，判断反色图像中每行是否出现了白点，即原图中该行是否存在黑点，如果存在则表明该行存在汉字。

再次扫描，从第一行开始到倒数第二行，判断此行与下一行反色后白点总数是否满足一定条件。如果此行没有白点而下一行白点总数不为0，则下一行是汉字的上边界；如果此行白点总数不为0而下一行没有白点，则此行是汉字的下边界。

流程图：

代码：

int CVICALLBACK rowSplit (int panel, int control, int event, void *callbackData, int eventData1, int eventData2)
{
	Point point;
	PixelValue grayLevel;
	// 每行文字上界和下界的数目
	int topm=0, botm=0; 
	// 获取输入图像的宽高
	imaqGetImageSize (srcImage, &width, &height); 
	// 每行（反色后）白点的数目
	int *pt = calloc(height, sizeof(int)); 
	
	switch (event)
	{
		case EVENT_COMMIT:
		// 出现（反色后）白色像素则确定边界 
		for(int h = 0; h < height; h++)
		{   for(int w = 0; w < width; w++)
		    {   point.x = w;
				point.y = h;
				imaqGetPixel(binImage, point, &grayLevel);
				if(grayLevel.grayscale == 255.0)
					*(pt + h) = *(pt + h) + 1;
	  	     }
		}
		// 记录每行文字上界和下界
		for(int h = 0; h < height - 1; h++)
		{   
			if(*(pt + h) == 0 & *(pt + h + 1) > 0) 
			{
				topRow[topm++] = h; 
				num_row = num_row + 1; 
			}
			if(*(pt + h) > 0 & *(pt + h + 1) == 0) 
				bottomRow[botm++] = h; 
		}
		// 记录行分割后每行文字的高度
		for(int topm = 0; topm < num_row; topm++)
			_height[topm] = bottomRow[topm] - topRow[topm]; 
		break;
	}
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

列分割

任务：

确定每个文字的开始列和结束列的位置。

步骤：

在行分割的基础上，先进行行扫描，然后进行列扫描，判断一行汉字里的每一列是否出现了白点，即原图中该列是否存在黑点，如果存在则表明该列存在汉字。

再次扫描，从每一行的第一列开始扫描到倒数第二列，判断此列与下一列反色后白点总数是否满足一定条件。如果此列没有白点而下一列白点总数不为0，则下一列是字的左边界；如果此列白点总数不为0而下一列没有白点，则此列是字的右边界。

代码：

for(h = 0; h < num_row; h++)
{
	i = 0, j = 0;
	// 出现（反色后）白色像素则确定边界 
	for(int x = 0; x < width; x++)
	{   
		for(int y = topRow[h]; y <= bottonRow[h]; y++)
		{   
			point.x = x;
			point.y = y;
			imaqGetPixel(binImage, point, &grayLevel);
			if(grayLevel.grayscale == 255.0) 
				 *(pt + h * width + x) = *(pt + h * width + x) + 1; 
			}
		}
		// 记录每行文字左界和右界
		for(int x = 0; x < width - 1; x++)
		{   
			if(*(pt + h * width + x) == 0 & *(pt + h * width + x + 1) > 0)   
					leftMargin[h][i++] = x;
			if(*(pt + h * width + x) > 0 & *(pt + h * width + x + 1) == 0)    
			{
				rightMargin[h][j++] = x; 
				num_col[h] = num_col[h] + 1;
			}
		}
	}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

列分割的原理和行分割基本一致，但是有可能出现误分割的情况（字中间存在空隙，即某行文字中某列反色后白色像素点数目为0）。

左右结构字体防误切割

任务：

识别出类似于“八”和“川”这种可能会被误分割成两部分或三部分的字。

步骤：

1.对于“八”型的字：
如果列分割的时候被分成第h行的第i个和第i+1个字，则根据第i个和第i+1个字的左右边界坐标值是否满足一定条件，来判断是否需要合并。

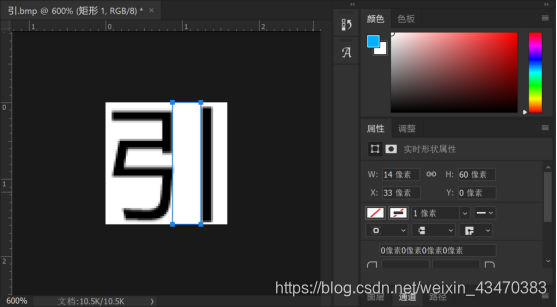
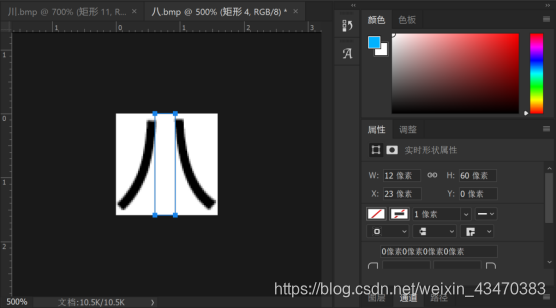
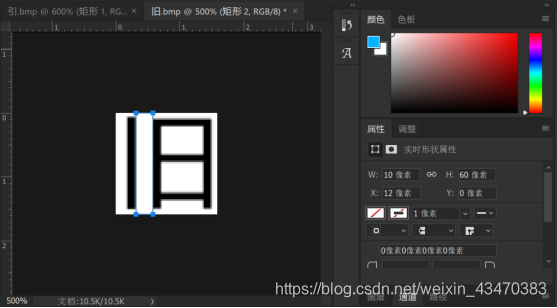
通过分析字形，确定判断条件：
(1) 第i+1个字的左边界与第i个字的右边界相距小于文字高度的三分之一；
(2) 第i+1个字的右边界与第i个字的左边界相距小于文字高度；
(3) 第i+2个字的右边界与第i个字的左边界相距大于文字高度。
以上三个条件都满足，则为“八”型的字。

对于“八”型的字，将初次列分割得到第i个和第i+1个字的左右边界合并，并将该行字的个数减去1。

2.对于“川”型的字：
如果列分割的时候被分成第h行的第i个、第i+1个字和第i+2个字，则根据第i个、第i+1个字和第i+2个字的左右边界坐标值是否满足一定条件，来判断是否需要合并。

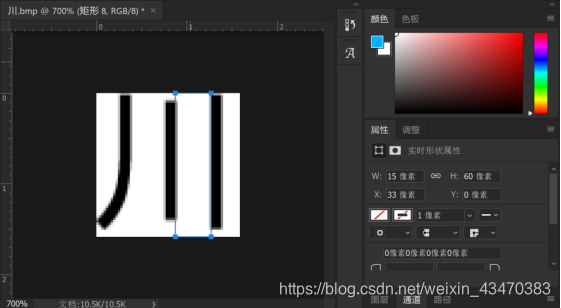
通过分析字形，确定判断条件：
(1) 第i+2个字的左边界与第i+1个字的右边界相距小于文字高度的三分之一；
(2) 第i+1个字的左边界与第i个字的右边界相距小于文字高度的三分之一；
(3) 第i+2个字的右边界与第i个字的左边界相距小于文字高度；
(4) 第i+3个字的右边界与第i个字的左边界相距大于文字高度。
以上条件(1)和(2)满足任意一条，同时满足条件(3)和(4)，则为“川”型的字。

对于“川”型的字，将初次列分割得到第i个、第i+1个和第i+2个字的左右边界合并，并将该行字的个数减去2。

流程图：

代码：

for(i = 0; i < num_col[h]; i++)
{   
	// 判断是否为“八”字这类容易被误分割成两部分的字，并对此进行合并
	if((leftMargin[h][i+1] - rightMargin[h][i] <= _height[h]/3) && (rightMargin[h][i+1] - leftMargin[h][i] <= _height[h]) 
		&& (rightMargin[h][i+2] - leftMargin[h][i] >= _height[h]))													 
	{   
		for(g = i; g < num_col[h]; g++)
			rightMargin[h][g] = rightMargin[h][g+1]; 
		for(j = i + 1; j < num_col[h]; j++)
			leftMargin[h][j] = leftMargin[h][j+1]; 
			num_col[h] = num_col[h] - 1; 
	}
	// 判断是否为“川”字这类容易被误分割成三部分的字，并对此进行合并  
	if(((leftMargin[h][i+2] - rightMargin[h][i+1] <= _height[h]/3) || (leftMargin[h][i+1] - rightMargin[h][i] <= _height[h]/3))
		&& (rightMargin[h][i+2] - leftMargin[h][i] <= _height[h]) && (rightMargin[h][i+3] - leftMargin[h][i] >= _height[h]))
	{   
		for(g = i;g < num_col[h]; g++)
			rightMargin[h][g] = rightMargin[h][g+2]; 
		for(j = i + 1; j < num_col[h]; j++)
			leftMargin[h][j] = leftMargin[h][j+2]; 
			num_col[h] = num_col[h] - 2; 
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

分割效果