- 1【SpringCloud】从实际业务问题出发去分析Eureka-Server端源码
- 2[附源码]Python计算机毕业设计Django点餐系统_点餐系统源码django
- 3硬盘出现“I/O设备错误的解决方法
- 4android之使用Soap协议调用webservice实现手机归属地查询_soap userid
- 5MySQL锁定状态查看相关命令_mysql table in_use
- 6Random快速产生相同随机数的原因及解决方案_common lang3 同一时刻生成随机数一样怎么破
- 7NLP大模型微调原理
- 8MySQL的数据类型
- 9MySQL深入学习(二七):性能分析工具的使用_innodb_rows_deleted
- 10打造专业级ChatGPT风格聊天界面:SpringBoot与Vue实现动态打字机效果,附完整前后端源码
AES加密原理分部详解及c语言代码实现思路_用c语言实现分组加密算法aes
赞
踩
在这里虽然有提及到AES解密,但先只讲加密,解密会后续补上。
AES简介
AES是一种分组加密算法,明文分组大小为128位,密钥长度有128、192、256位三种。AES加密在加密前先将明文分成128位一组的若干组,再分组进行加密。在AES加密中一个字由四个字节组成。
AES加密及解密流程
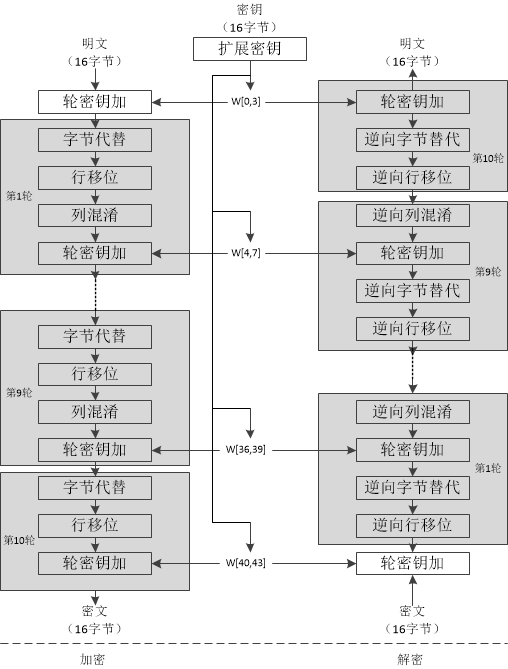
AES加密的几个模块及详解
前言
在对AES加密模块及其代码进行讲解前先对c语言中关于数组的使用方法及c实现AES过程中所涉及到的一些运算符进行一些讲解:
数组的定义:
一维数组:
int a[4];//定义一个一维长度为四的数组
int b[4]={0,1,2,3};//定义一个一维长度为四的数组并初始化为{0,1,2,3}
int *p=&b[0];//定义一个int类型指针指向b[0]
*p=4;//令指针p指向的b[0]=4
*(p+1)=5;//令指针p指向的b[0]的下一个数组元素b[1]=5;
- 1
- 2
- 3
- 4
- 5
二维数组:
int a[4][4]=
{
0,1,2,3,
4,5,6,7,
8,9,10,11,
12,13,14,15
};
//定义一个4*4的二维数组并初始化为:
//{0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15}
int *p=&a[0][0];
*(p+2*4+1)=5;//令a[2][1]=5
//指针(p+j*4+i)的意义是:
//相对于二维数组a[4][4],指针(p+j*4+i)等价于a[j][i]
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
运算符:
“^”为异或运算,
任意两个整数a,b进行异或运算a^b的结果与将其转换成二进制后再进行异或运算的结果是相同的。
实际上数是客观存在的,数的进制表示只是数的表现形式,数的任何操作都是对数本身进行操作,故16进制数0x16与0x23异或运算等价于二进制数0b00010110与0b00100011异或运算。
轮密钥加
算法原理
AES加密在第一轮加密前先进行了一次轮密钥加,第一轮加密前的轮密钥加实际上是对明文分组和初始密钥进行了一次异或运算。
c代码实现思路
如何实现用c语言实现轮密钥加呢?
首先,明文分组与密钥都为128位的其实等于16个字节,将明文与密钥分别对应的16个字节行向优先填入两个4*4的矩阵中。
先定义两个4*4的二维数组:
int plaintext[4][4],key[4][4];
- 1
并将明文分组与密钥行向优先填入这两个数组;
再定义两个指针分别指向plaintext[0][0]、key[0][0]:
int *p=&plaintext[0][0];int *k=&key[0][0];
- 1
对于使这两个数组对应的元素准确异或可以用for语句来实现:
for(j=0;j<4;j++)
for(i=0;i<4;i++)
plaintext[j][i]=plaintext[j][i]^key[j][i];
- 1
- 2
- 3
因为主函数要将轮密钥加作为副函数来调用,所以将数组指针作为参数来实现这个模块。
c代码实现
void addbyte16(int *p,int *k)//轮密钥加,结果保存在左参数,也为4*4数组异或
{
int i,j;
for(j=0;j<4;j++)
for(i=0;i<4;i++)
*(p+j*4+i)=*(p+j*4+i)^*(k+j*4+i);
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
可以看出轮密钥加的函数实际上是两个4*4数组进行对应异或,所以对其命名为addbyte16。
字节代替(s盒)
算法原理
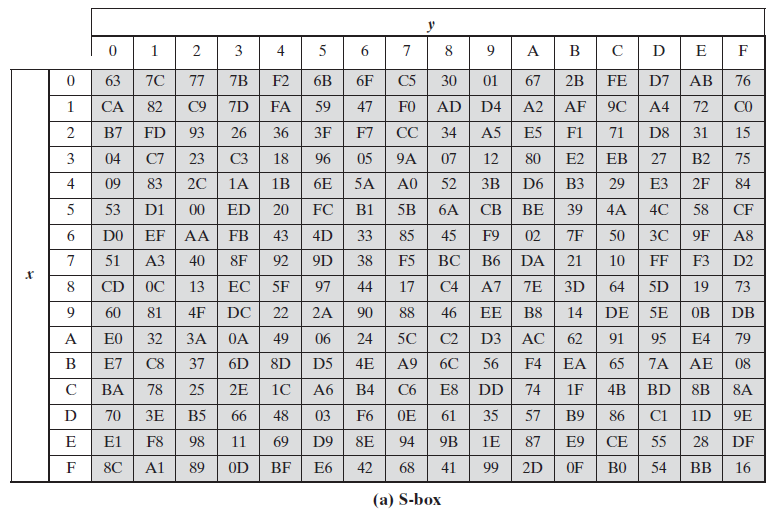
s盒是将输入的16字节数每个字节都经过一次查表变换生成密文,而查表变换便是:
将输入的字节例0x16的高四位即0x1作为行值低四位即0x6作为列值查上面的表中的第0x1行0x6列所得的值作为经查表变换后输出的值即0x47。
c代码实现思路
先定义一个16*16(256)的一维数组int s[256];,并将s-box表输入其中;
当输入一个字节0xmn时它在s表中的位置为0xm行0xn列,在一维数组s中的位置为[0xm * 16+0xn],而[0xm * 16+0xn]=0xmn,故可以使输入的字节作为数组s的标号即s[0xmn]作为输出。
c代码实现
void she(int *p)//S盒 { int i; int s[256] = { 0x63,0x7c,0x77,0x7b,0xf2,0x6b,0x6f,0xc5,0x30,0x01,0x67,0x2b,0xfe,0xd7,0xab,0x76, 0xca,0x82,0xc9,0x7d,0xfa,0x59,0x47,0xf0,0xad,0xd4,0xa2,0xaf,0x9c,0xa4,0x72,0xc0, 0xb7,0xfd,0x93,0x26,0x36,0x3f,0xf7,0xcc,0x34,0xa5,0xe5,0xf1,0x71,0xd8,0x31,0x15, 0x04,0xc7,0x23,0xc3,0x18,0x96,0x05,0x9a,0x07,0x12,0x80,0xe2,0xeb,0x27,0xb2,0x75, 0x09,0x83,0x2c,0x1a,0x1b,0x6e,0x5a,0xa0,0x52,0x3b,0xd6,0xb3,0x29,0xe3,0x2f,0x84, 0x53,0xd1,0x00,0xed,0x20,0xfc,0xb1,0x5b,0x6a,0xcb,0xbe,0x39,0x4a,0x4c,0x58,0xcf, 0xd0,0xef,0xaa,0xfb,0x43,0x4d,0x33,0x85,0x45,0xf9,0x02,0x7f,0x50,0x3c,0x9f,0xa8, 0x51,0xa3,0x40,0x8f,0x92,0x9d,0x38,0xf5,0xbc,0xb6,0xda,0x21,0x10,0xff,0xf3,0xd2, 0xcd,0x0c,0x13,0xec,0x5f,0x97,0x44,0x17,0xc4,0xa7,0x7e,0x3d,0x64,0x5d,0x19,0x73, 0x60,0x81,0x4f,0xdc,0x22,0x2a,0x90,0x88,0x46,0xee,0xb8,0x14,0xde,0x5e,0x0b,0xdb, 0xe0,0x32,0x3a,0x0a,0x49,0x06,0x24,0x5c,0xc2,0xd3,0xac,0x62,0x91,0x95,0xe4,0x79, 0xe7,0xc8,0x37,0x6d,0x8d,0xd5,0x4e,0xa9,0x6c,0x56,0xf4,0xea,0x65,0x7a,0xae,0x08, 0xba,0x78,0x25,0x2e,0x1c,0xa6,0xb4,0xc6,0xe8,0xdd,0x74,0x1f,0x4b,0xbd,0x8b,0x8a, 0x70,0x3e,0xb5,0x66,0x48,0x03,0xf6,0x0e,0x61,0x35,0x57,0xb9,0x86,0xc1,0x1d,0x9e, 0xe1,0xf8,0x98,0x11,0x69,0xd9,0x8e,0x94,0x9b,0x1e,0x87,0xe9,0xce,0x55,0x28,0xdf, 0x8c,0xa1,0x89,0x0d,0xbf,0xe6,0x42,0x68,0x41,0x99,0x2d,0x0f,0xb0,0x54,0xbb,0x16 }; for (i = 0; i < 16; i++)*(p + i) = s[*(p + i)]; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
行移位
算法原理
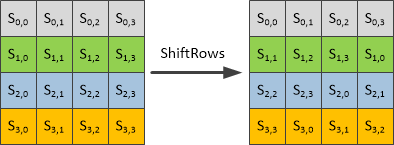
行移位是使如上图这样的4*4矩阵第1行左移0位、第2行左移1位、第三行左移2位、第四行左移3位。
c代码实现思路
在c语言中对于4*4的数组的行列是从0~3编号的,即:
第0行左移0位、第1行左移1位、第2行左移2位、第3行左移3位。
对于左移可以先:int b[4][4],在b中保留左移后的结果。通过b[j][i]=*(p+j*4+(i+j)%4);来实现左移。最后再将b中的结果填入到原数组中。
c代码实现
void left(int *p)//行移位
{
int i, j;
int b[4][4];
for (j = 0; j < 4; j++)
for (i = 0; i < 4; i++)
b[j][i] = *(p + j * 4 + (i + j) % 4);
for (j = 0; j < 4; j++)
for (i = 0; i < 4; i++)
*(p + i + j * 4) = b[j][i];
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
列混淆
算法原理
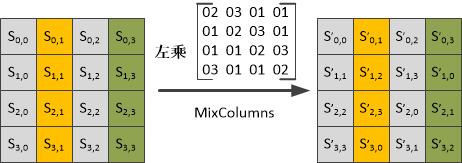
列混淆是将输入的4*4矩阵左乘一个常熟矩阵(常数矩阵是一个常态,固定不变),在这里左乘是矩阵的左乘,但又有所不同,以上图中的矩阵左乘为例:
s'0,0=0x02*s0,0+0x03*s1,0+0x01*s2,0+0x01*s3.0
- 1
在上面的式子中,乘法为有限域GF(2^8)上的乘法,
加法为有限域GF(2^8)上的加法即异或。
列混淆的左乘与普通矩阵的左乘不同之处就在于乘法为有限域GF(2^8)上的乘法,
加法为有限域GF(2^8)上的加法即异或。
c代码实现思路
为了便于说明,在接下来的叙述中乘就是有限域GF(2^8)上的乘法。
先对乘法进行定义:
列混淆中的有限域GF(2^8)上的乘法
因为常数矩阵是由0x01、0x02、0x03这三个数组成,所以只需考虑这三个数与其他数相乘。
0x01:
0x01与任何数相乘都为这个数本身。
0x02:
对于a*0x02(即0000 0010)有两种情况:
(1)、当a小于0x80(即1000 0000)时a*0000 0010等于将a最高位去掉再在末尾补0的值,例:
a=0010 0011,
a*0000 0010=0100 0110;
a=0111 0010,
a*0000 0010=1110 0100;
- 1
- 2
- 3
- 4
(2)、当a大于等于0x80时a*0000 0010等于将a最高位去掉再在末尾补0后再和0x1b(即0001 1011)异或的值,例:
a=1010 0011,
a*0000 0010=0100 0110
^0001 1011
=0101 1101;
- 1
- 2
- 3
- 4
0x30:
因为 0x03=0000 0011=(0000 0001^0000 0010),
所以 a*0x03=(a*0000 0001)^(a*0000 0010)=a^(a*0000 0010);
- 1
- 2
同样的,对于这里的a*0x02(即0000 0010)也是有上面关于0x02的叙述中的两种情况。
列混淆中的有限域GF(2^8)上的乘法c代码实现
int mul(int b,int a)//有限域上的乘法,只定义了01、02、03与其他数相乘
{
if (b == 0x02)
{
if (a < 0x80)a = (a * 0x02);
else a = ((a % 0x80) * 0x02) ^ 0x1b;
}
if (b == 0x03)
{
if (a < 0x80)b = (a * 0x02);
else b = ((a % 0x80) * 0x02) ^ 0x1b;
a = a^b;
}
return a;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
矩阵乘法
如上图,矩阵C中的元素的标号决定了这个元素由矩阵A与B中哪些元素进行计算求得(行号决定了取A中哪一行的元素,列号决定了取B中哪一列的元素),设C[j][i],则:
C[j][i]=aj,1*b1,i+aj,2*b2,i+aj,3*b3,i+aj,4*b4,i;
- 1
矩阵乘法c代码实现
for(j=0;j<4;j++)
for(i=0;i<4;i++)
c[j][i]=aj,1*b1,i+aj,2*b2,i+aj,3*b3,i+aj,4*b4,i;
- 1
- 2
- 3
列混淆c代码实现
因为输入的4*4矩阵中的元素不只使用一次,故要不改动输入的矩阵,用一个4*4数组存放运算结果。
void column(int *p, int *q)//列混淆
{
int i, j;
int a[4][4];
for (j = 0; j < 4; j++)for (i = 0; i < 4; i++)
{
a[j][i] = mul(*(q + j * 4 + 0), *(p + 0 * 4 + i)) ^ mul(*(q + j * 4 + 1), *(p + 1 * 4 + i)) ^
mul(*(q + j * 4 + 2), *(p + 2 * 4 + i)) ^ mul(*(q + j * 4 + 3), *(p + 3 * 4 + i));
}
for (j = 0; j < 4; j++)for (i = 0; i < 4; i++)*(p + j * 4 + i) = a[j][i];
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
密钥扩展
算法原理
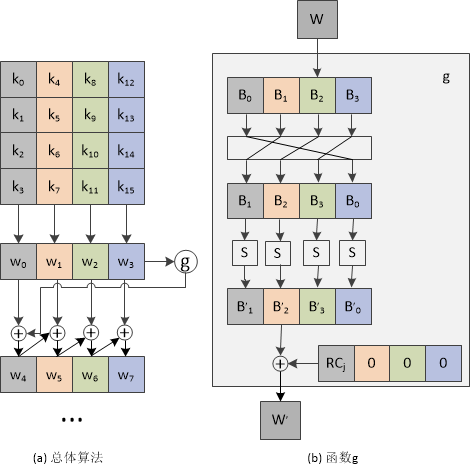
密钥扩展是:在第一轮时将输入的初始密钥数组按上图左上角的方式第一列组成一个竖向数组w0、第二组成一个竖向数组w2、第三列组成一个竖向数组w3、第四列组成一个竖向数组w4,将w3经过g函数变换后与w1异或得到w4,将w4与w1异或得到w5,将w5与w2异或得到w6,将w6与w3异或得到w7,接下来的第二轮、第三轮等重复第一轮的变换得到,w8、w9等。
而g函数是将输入的1*4竖向数组变成横向数组进行左移一位操作后将每个字节进行s盒变换,再将第一个字节与RC数组中的一个字节进行异或,与哪个字节异或取决于当前的轮数。
c代码实现思路
第一步将二维数组分成四个竖向数组,在c语言中没有竖向数组,可以将竖向数组改为横向数组,即将得到的竖向数组按顺序存放在一个一维数组中。即:
for (i = 0; i < 4; i++)a[i] = *(p + i * 4 + 0);
for (i = 0; i < 4; i++)b[i] = *(p + i * 4 + 1);
for (i = 0; i < 4; i++)c[i] = *(p + i * 4 + 2);
for (i = 0; i < 4; i++)d[i] = *(p + i * 4 + 3);
- 1
- 2
- 3
- 4
g-s盒实现
g-s盒与s盒很相似,区别在于g-s盒是对1*4数组的变换操作。
void gshe(int *p)//g-S盒 { int i; int s[256] = { 0x63,0x7c,0x77,0x7b,0xf2,0x6b,0x6f,0xc5,0x30,0x01,0x67,0x2b,0xfe,0xd7,0xab,0x76, 0xca,0x82,0xc9,0x7d,0xfa,0x59,0x47,0xf0,0xad,0xd4,0xa2,0xaf,0x9c,0xa4,0x72,0xc0, 0xb7,0xfd,0x93,0x26,0x36,0x3f,0xf7,0xcc,0x34,0xa5,0xe5,0xf1,0x71,0xd8,0x31,0x15, 0x04,0xc7,0x23,0xc3,0x18,0x96,0x05,0x9a,0x07,0x12,0x80,0xe2,0xeb,0x27,0xb2,0x75, 0x09,0x83,0x2c,0x1a,0x1b,0x6e,0x5a,0xa0,0x52,0x3b,0xd6,0xb3,0x29,0xe3,0x2f,0x84, 0x53,0xd1,0x00,0xed,0x20,0xfc,0xb1,0x5b,0x6a,0xcb,0xbe,0x39,0x4a,0x4c,0x58,0xcf, 0xd0,0xef,0xaa,0xfb,0x43,0x4d,0x33,0x85,0x45,0xf9,0x02,0x7f,0x50,0x3c,0x9f,0xa8, 0x51,0xa3,0x40,0x8f,0x92,0x9d,0x38,0xf5,0xbc,0xb6,0xda,0x21,0x10,0xff,0xf3,0xd2, 0xcd,0x0c,0x13,0xec,0x5f,0x97,0x44,0x17,0xc4,0xa7,0x7e,0x3d,0x64,0x5d,0x19,0x73, 0x60,0x81,0x4f,0xdc,0x22,0x2a,0x90,0x88,0x46,0xee,0xb8,0x14,0xde,0x5e,0x0b,0xdb, 0xe0,0x32,0x3a,0x0a,0x49,0x06,0x24,0x5c,0xc2,0xd3,0xac,0x62,0x91,0x95,0xe4,0x79, 0xe7,0xc8,0x37,0x6d,0x8d,0xd5,0x4e,0xa9,0x6c,0x56,0xf4,0xea,0x65,0x7a,0xae,0x08, 0xba,0x78,0x25,0x2e,0x1c,0xa6,0xb4,0xc6,0xe8,0xdd,0x74,0x1f,0x4b,0xbd,0x8b,0x8a, 0x70,0x3e,0xb5,0x66,0x48,0x03,0xf6,0x0e,0x61,0x35,0x57,0xb9,0x86,0xc1,0x1d,0x9e, 0xe1,0xf8,0x98,0x11,0x69,0xd9,0x8e,0x94,0x9b,0x1e,0x87,0xe9,0xce,0x55,0x28,0xdf, 0x8c,0xa1,0x89,0x0d,0xbf,0xe6,0x42,0x68,0x41,0x99,0x2d,0x0f,0xb0,0x54,0xbb,0x16 }; for (i = 0; i < 4; i++)*(p + i) = s[*(p + i)]; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
1*4数组的加法
1*4数组的加法与4*4数组加法相似,区别在于是对于1*4数组的操作。
void addbyte4(int *p, int *q)//1*4矩阵字节加法,结果保存到左加数
{
int i;
for (i = 0; i < 4; i++)
*(p + i) = *(p + i) ^ *(q + i);
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
g函数
在g函数中定义RC数组,并将加密轮数作为一个参数来决定异或的RC数组中的哪个字节。因要进行左移一位操作,故先将输入的数组第一个元素保存在a,for (i = 0; i < 3; i++)*(p+i) = *(p + i + 1);后再*(p + 3) = a;
void g(int *p,int j)//g函数
{
int rc[10] = { 0x01,0x02,0x04,0x08,0x10,0x20,0x40,0x80,0x1b,0x36 };
int i,a = *p;
for (i = 0; i < 3; i++)*(p+i) = *(p + i + 1);*(p + 3) = a;
gshe(p);
*p = *p^rc[j];
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
在进行g函数变换和异或变换后将四个一维竖向数组还原成原来的行向4*4的二维数组。
for (i = 0; i < 4; i++)*(p + i * 4 + 0) = a[i];
for (i = 0; i < 4; i++)*(p + i * 4 + 1) = b[i];
for (i = 0; i < 4; i++)*(p + i * 4 + 2) = c[i];
for (i = 0; i < 4; i++)*(p + i * 4 + 3) = d[i];
- 1
- 2
- 3
- 4
c代码实现
在这里因为w3、w7等数组要利用两次故定义额外一个数组等于w3、w7等数组。
将加密轮数j作为输入参数。
void keyextension(int *p, int j)//密钥扩展 { int a[4], b[4], c[4], d[4], d1[4]; int i, *q1 = &a[0], *q2 = &b[0], *q3 = &c[0], *q4 = &d[0], *q5 = &d1[0]; for (i = 0; i < 4; i++)a[i] = *(p + i * 4 + 0); for (i = 0; i < 4; i++)b[i] = *(p + i * 4 + 1); for (i = 0; i < 4; i++)c[i] = *(p + i * 4 + 2); for (i = 0; i < 4; i++)d[i] = *(p + i * 4 + 3); for (i = 0; i < 4; i++)d1[i] = *(p + i * 4 + 3); g(q5, j); addbyte4(q1, q5); addbyte4(q2, q1); addbyte4(q3, q2); addbyte4(q4, q3); for (i = 0; i < 4; i++)*(p + i * 4 + 0) = a[i]; for (i = 0; i < 4; i++)*(p + i * 4 + 1) = b[i]; for (i = 0; i < 4; i++)*(p + i * 4 + 2) = c[i]; for (i = 0; i < 4; i++)*(p + i * 4 + 3) = d[i]; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
主函数设计思路
AES中在进行第一轮加密前先进行了一次轮密钥加:
//第一轮前
addbyte16(p,k);
- 1
- 2
在十轮加密中除了第十轮加密有所不同外其它九轮是一样的:
//第一轮到第九轮(0~8)
for(i=0;i<9;i++)
{
she(p);
left(p);
column(p,q);
keyextension(k,i);
addbyte16(p,k);
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
第十轮相对于其他九轮少了列混淆:
//第十轮
she(p);
left(p);
keyextension(k,9);
addbyte16(p,k);
- 1
- 2
- 3
- 4
- 5
主函数
int main(int argc, char *argv[]) { int i, j; int u[4][4],key[4][4]; //输入明文 printf("input plaintext:\n"); for (j = 0; j < 4; j++) for (i = 0; i < 4; i++) scanf("%x",&u[j][i]); //输入密钥 printf("input key:\n"); for (j = 0; j < 4; j++) for (i = 0; i < 4; i++) scanf("%x",&key[j][i]); //列混淆常数矩阵 int u1[4][4] = { 0x02,0x03,0x01,0x01, 0x01,0x02,0x03,0x01, 0x01,0x01,0x02,0x03, 0x03,0x01,0x01,0x02 }; int *p = &u[0][0]; int *q = &u1[0][0]; int *k = &key[0][0]; //第一轮前 addbyte16(p,k); //第一轮到第九轮(0~8) for(i=0;i<9;i++) { she(p); left(p); column(p,q); keyextension(k,i); addbyte16(p,k); } //第十轮 she(p); left(p); keyextension(k,9); addbyte16(p,k); //密文输出 printf("ciphertext:\n"); for (i = 0; i < 4; i++) { for (j = 0; j < 4; j++)printf("%x ", u[i][j]); printf("\n"); } system("pause"); return 0; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
AES c语言实现
#include <stdio.h> #include <stdlib.h> void she(int *p)//S盒 { int i; int s[256] = { 0x63,0x7c,0x77,0x7b,0xf2,0x6b,0x6f,0xc5,0x30,0x01,0x67,0x2b,0xfe,0xd7,0xab,0x76, 0xca,0x82,0xc9,0x7d,0xfa,0x59,0x47,0xf0,0xad,0xd4,0xa2,0xaf,0x9c,0xa4,0x72,0xc0, 0xb7,0xfd,0x93,0x26,0x36,0x3f,0xf7,0xcc,0x34,0xa5,0xe5,0xf1,0x71,0xd8,0x31,0x15, 0x04,0xc7,0x23,0xc3,0x18,0x96,0x05,0x9a,0x07,0x12,0x80,0xe2,0xeb,0x27,0xb2,0x75, 0x09,0x83,0x2c,0x1a,0x1b,0x6e,0x5a,0xa0,0x52,0x3b,0xd6,0xb3,0x29,0xe3,0x2f,0x84, 0x53,0xd1,0x00,0xed,0x20,0xfc,0xb1,0x5b,0x6a,0xcb,0xbe,0x39,0x4a,0x4c,0x58,0xcf, 0xd0,0xef,0xaa,0xfb,0x43,0x4d,0x33,0x85,0x45,0xf9,0x02,0x7f,0x50,0x3c,0x9f,0xa8, 0x51,0xa3,0x40,0x8f,0x92,0x9d,0x38,0xf5,0xbc,0xb6,0xda,0x21,0x10,0xff,0xf3,0xd2, 0xcd,0x0c,0x13,0xec,0x5f,0x97,0x44,0x17,0xc4,0xa7,0x7e,0x3d,0x64,0x5d,0x19,0x73, 0x60,0x81,0x4f,0xdc,0x22,0x2a,0x90,0x88,0x46,0xee,0xb8,0x14,0xde,0x5e,0x0b,0xdb, 0xe0,0x32,0x3a,0x0a,0x49,0x06,0x24,0x5c,0xc2,0xd3,0xac,0x62,0x91,0x95,0xe4,0x79, 0xe7,0xc8,0x37,0x6d,0x8d,0xd5,0x4e,0xa9,0x6c,0x56,0xf4,0xea,0x65,0x7a,0xae,0x08, 0xba,0x78,0x25,0x2e,0x1c,0xa6,0xb4,0xc6,0xe8,0xdd,0x74,0x1f,0x4b,0xbd,0x8b,0x8a, 0x70,0x3e,0xb5,0x66,0x48,0x03,0xf6,0x0e,0x61,0x35,0x57,0xb9,0x86,0xc1,0x1d,0x9e, 0xe1,0xf8,0x98,0x11,0x69,0xd9,0x8e,0x94,0x9b,0x1e,0x87,0xe9,0xce,0x55,0x28,0xdf, 0x8c,0xa1,0x89,0x0d,0xbf,0xe6,0x42,0x68,0x41,0x99,0x2d,0x0f,0xb0,0x54,0xbb,0x16 }; for (i = 0; i < 16; i++)*(p + i) = s[*(p + i)]; } void gshe(int *p)//g-S盒 { int i; int s[256] = { 0x63,0x7c,0x77,0x7b,0xf2,0x6b,0x6f,0xc5,0x30,0x01,0x67,0x2b,0xfe,0xd7,0xab,0x76, 0xca,0x82,0xc9,0x7d,0xfa,0x59,0x47,0xf0,0xad,0xd4,0xa2,0xaf,0x9c,0xa4,0x72,0xc0, 0xb7,0xfd,0x93,0x26,0x36,0x3f,0xf7,0xcc,0x34,0xa5,0xe5,0xf1,0x71,0xd8,0x31,0x15, 0x04,0xc7,0x23,0xc3,0x18,0x96,0x05,0x9a,0x07,0x12,0x80,0xe2,0xeb,0x27,0xb2,0x75, 0x09,0x83,0x2c,0x1a,0x1b,0x6e,0x5a,0xa0,0x52,0x3b,0xd6,0xb3,0x29,0xe3,0x2f,0x84, 0x53,0xd1,0x00,0xed,0x20,0xfc,0xb1,0x5b,0x6a,0xcb,0xbe,0x39,0x4a,0x4c,0x58,0xcf, 0xd0,0xef,0xaa,0xfb,0x43,0x4d,0x33,0x85,0x45,0xf9,0x02,0x7f,0x50,0x3c,0x9f,0xa8, 0x51,0xa3,0x40,0x8f,0x92,0x9d,0x38,0xf5,0xbc,0xb6,0xda,0x21,0x10,0xff,0xf3,0xd2, 0xcd,0x0c,0x13,0xec,0x5f,0x97,0x44,0x17,0xc4,0xa7,0x7e,0x3d,0x64,0x5d,0x19,0x73, 0x60,0x81,0x4f,0xdc,0x22,0x2a,0x90,0x88,0x46,0xee,0xb8,0x14,0xde,0x5e,0x0b,0xdb, 0xe0,0x32,0x3a,0x0a,0x49,0x06,0x24,0x5c,0xc2,0xd3,0xac,0x62,0x91,0x95,0xe4,0x79, 0xe7,0xc8,0x37,0x6d,0x8d,0xd5,0x4e,0xa9,0x6c,0x56,0xf4,0xea,0x65,0x7a,0xae,0x08, 0xba,0x78,0x25,0x2e,0x1c,0xa6,0xb4,0xc6,0xe8,0xdd,0x74,0x1f,0x4b,0xbd,0x8b,0x8a, 0x70,0x3e,0xb5,0x66,0x48,0x03,0xf6,0x0e,0x61,0x35,0x57,0xb9,0x86,0xc1,0x1d,0x9e, 0xe1,0xf8,0x98,0x11,0x69,0xd9,0x8e,0x94,0x9b,0x1e,0x87,0xe9,0xce,0x55,0x28,0xdf, 0x8c,0xa1,0x89,0x0d,0xbf,0xe6,0x42,0x68,0x41,0x99,0x2d,0x0f,0xb0,0x54,0xbb,0x16 }; for (i = 0; i < 4; i++)*(p + i) = s[*(p + i)]; } void left(int *p)//行移位 { int i, j; int b[4][4]; for (j = 0; j < 4; j++) for (i = 0; i < 4; i++) b[j][i] = *(p + j * 4 + (i + j) % 4); for (j = 0; j < 4; j++) for (i = 0; i < 4; i++) *(p + i + j * 4) = b[j][i]; } void addbyte16(int *p, int *q)//4*4矩阵字节加法,结果保存到左加数,也为轮密钥加 { int i, j; for (j = 0; j < 4; j++)for (i = 0; i < 4; i++) *(p + j * 4 + i) = *(p + j * 4 + i) ^ *(q + j * 4 + i); } void addbyte4(int *p, int *q)//1*4矩阵字节加法,结果保存到左加数 { int i; for (i = 0; i < 4; i++) *(p + i) = *(p + i) ^ *(q + i); } int mul(int b,int a)//有限域上的乘法,只定义了01、02、03与其他数相乘 { if (b == 0x02) { if (a < 0x80)a = (a * 0x02); else a = ((a % 0x80) * 0x02) ^ 0x1b; } if (b == 0x03) { if (a < 0x80)b = (a * 0x02); else b = ((a % 0x80) * 0x02) ^ 0x1b; a = a^b; } return a; } void column(int *p, int *q)//列混淆 { int i, j; int a[4][4]; for (j = 0; j < 4; j++)for (i = 0; i < 4; i++) { a[j][i] = mul(*(q + j * 4 + 0), *(p + 0 * 4 + i)) ^ mul(*(q + j * 4 + 1), *(p + 1 * 4 + i)) ^ mul(*(q + j * 4 + 2), *(p + 2 * 4 + i)) ^ mul(*(q + j * 4 + 3), *(p + 3 * 4 + i)); } for (j = 0; j < 4; j++)for (i = 0; i < 4; i++)*(p + j * 4 + i) = a[j][i]; } void g(int *p,int j)//g函数 { int rc[10] = { 0x01,0x02,0x04,0x08,0x10,0x20,0x40,0x80,0x1b,0x36 }; int i,a = *p; for (i = 0; i < 3; i++)*(p+i) = *(p + i + 1);*(p + 3) = a; gshe(p); *p = *p^rc[j]; } void keyextension(int *p, int j)//密钥扩展 { int a[4], b[4], c[4], d[4], d1[4]; int i, *q1 = &a[0], *q2 = &b[0], *q3 = &c[0], *q4 = &d[0], *q5 = &d1[0]; for (i = 0; i < 4; i++)a[i] = *(p + i * 4 + 0); for (i = 0; i < 4; i++)b[i] = *(p + i * 4 + 1); for (i = 0; i < 4; i++)c[i] = *(p + i * 4 + 2); for (i = 0; i < 4; i++)d[i] = *(p + i * 4 + 3); for (i = 0; i < 4; i++)d1[i] = *(p + i * 4 + 3); g(q5, j); addbyte4(q1, q5); addbyte4(q2, q1); addbyte4(q3, q2); addbyte4(q4, q3); for (i = 0; i < 4; i++)*(p + i * 4 + 0) = a[i]; for (i = 0; i < 4; i++)*(p + i * 4 + 1) = b[i]; for (i = 0; i < 4; i++)*(p + i * 4 + 2) = c[i]; for (i = 0; i < 4; i++)*(p + i * 4 + 3) = d[i]; } int main(int argc, char *argv[]) { int i, j; int u[4][4],key[4][4]; //输入明文 printf("input plaintext:\n"); for (j = 0; j < 4; j++) for (i = 0; i < 4; i++) scanf("%x",&u[j][i]); //输入密钥 printf("input key:\n"); for (j = 0; j < 4; j++) for (i = 0; i < 4; i++) scanf("%x",&key[j][i]); //列混淆常数矩阵 int u1[4][4] = { 0x02,0x03,0x01,0x01, 0x01,0x02,0x03,0x01, 0x01,0x01,0x02,0x03, 0x03,0x01,0x01,0x02 }; int *p = &u[0][0]; int *q = &u1[0][0]; int *k = &key[0][0]; //第一轮前 addbyte16(p,k); //第一轮到第九轮(0~8) for(i=0;i<9;i++) { she(p); left(p); column(p,q); keyextension(k,i); addbyte16(p,k); } //第十轮 she(p); left(p); keyextension(k,9); addbyte16(p,k); //密文输出 printf("ciphertext:\n"); for (i = 0; i < 4; i++) { for (j = 0; j < 4; j++)printf("%x ", u[i][j]); printf("\n"); } system("pause"); return 0; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
- 160
- 161
- 162
- 163
- 164
- 165
- 166
- 167
- 168
- 169
- 170
- 171
- 172
- 173
- 174
- 175
- 176
- 177
- 178
- 179
- 180
- 181
- 182
- 183
- 184
- 185
- 186
- 187
- 188
- 189
- 190
- 191
- 192
- 193
- 194
- SpringBoot内置Tomcat,再默认设置中,Tomcat的最大线程数是200,最大连接数是10000。支持的并发量是指连接数,200个线程如何处理10000条连接的?Tomcat有两种处理连接的模式,一种是BIO,一个线程只处理一个... [详细]
赞
踩
- 零基础入门就得从最基本的变量,语法格式,数据类型,函数,作用域,模块等基本知识入手(有编程基础基础也得这么来)和篮球一样,先来三步上篮_python编程入门到实战python编程入门到实战Python零基础入门零基础入门就得从最基本的变量,... [详细]
赞
踩
- 但如果没有显示屏,比较麻烦。因此配置nomachine。_jetsonnano环境配置jetsonnano环境配置jetson烧写镜像在jetson上烧写镜像,并转移到ssd启动这里注意,windows和linux编码格式有所不同。部分电脑... [详细]
赞
踩
- 刷洛谷网也有一段时间了,但是一直进展不大,当我刷完新手前三关的时候,循环那关有道三连击的题目正是我在算法书上遇到的那道题,当时看着很烦,因为实在没有任何头绪,不过幸运的是洛谷网只要求每关作对三道题就可以通过,现在依旧被那道三连击的题目所烦扰... [详细]
赞
踩
- 1配置文件wisely.primary.datasource.driverClassName=oracle.jdbc.OracleDriverwisely.primary.datasource.url=jdbc\:oracle\:thin\... [详细]
赞
踩
- 如今,尽管SD-WAN技术在业内仍未有系统、标准的定义,但未来WAN传输将是软件定义的这一观点已成为业内共识:只有在应用识别能力、隧道加密能力、动态优化能力、应用可视化能力和零信任构架五大能力的支持下,一个具有商业化价值的SD-WAN基础服... [详细]
赞
踩
- 1、环境搭建Python由荷兰数学和计算机科学研究学会的GuidovanRossum于1990年代初设计。Python提供了高效的高级数据结构,还能简单有效地面向对象编程。Python具备可移植性,可以在多个平台运行,这里给大家带来的是Wi... [详细]
赞
踩
- 现在开发项目遇到一个问题,mac系统和windows下开发,对于mac下的sh脚本,想要在windows下也能正常执行,通过了解,安装cygwin,Cygwin是一个在windows平台上运行的类UNIX模拟环境基本操作命令:ls#以默认方... [详细]
赞
踩
- 我们发觉作用域解析操作符(::),作用是告诉编译器这个方法存在于何处,或者说是属于哪一个类。其实我们对这个不应该感到陌生,从一个开始小甲鱼就不提倡usingnamespacestd;这样偷懒的做法,所以我们是std::cout。。。事实上s... [详细]
赞
踩
- 不知道上一讲的大段代码大家看晕了没有。但是如果你仔细看了会发现,其实代码还是不全的。比如分词器我们就没讲。另外,13B比7B的改进点也没有讲。再有,对于13B需要多少显存我们也没说。13B光是模型加载就需要26GB的显存,加上推理需要的消i... [详细]
赞
踩
- 正文:有的时候,我们需要在php中利用到其他语言编写的dll类库,如C#编写的dll,方法就是利用PHPnewCOM方法来调用,在调用之前先要把dll库注册并把程序集放入到全局缓存中。1. 创建一个C#ClassLibrary,命名为:He... [详细]
赞
踩
- (1)为了提取信息更丰富的特征,提出了整合全局注意力机制(GAM)。该机制有效地捕获了特征的通道和空间方面,并增加了跨维交互的重要性。(2)为了进一步提高网络的性能,引入了ACMIX(一种结合自关注和卷积优点的混合模型)。(3)Yolov7... [详细]
赞
踩
- 首先,这是一道模拟题,但数据范围很大,1e18.所以,我们先暴力求解+打表,发现一下规律:#include
#include #include #include #definell... [详细] 赞
踩
- 目前来说Python是一门非常火爆的编程语言。Python在人工智能、机器学习、大数据、数据分析、网络爬虫等领域有了比较高的地位,可以说前景是非常好的。在编程领域也是非常适合作为兴趣培养的一门语言,相比较其他不少主流编程语言,有更好的可读性... [详细]
赞
踩
- 1.说明其他博客已经讲得很详细了,但是或多或少会有些问题,我自己安装了一遍发下了如下的一些注意事项,想安装的同学们注意了。假设你已经安装好了anaconda和py37。2.CUDA和cudnn安装cuda的时候,大的版本号一定要对,安装cu... [详细]
赞
踩
- CodeforcesRound#704(Div.2)-C.Maximumwidth传送门TimeLimit:2secondsMemoryLimit:512megabytesProblemDescriptionYourclassmate,wh... [详细]
赞
踩
- PDF到文本提取是自然语言处理和数据分析中的一项基本任务,它允许研究人员和数据分析师从PDF文件中包含的非结构化文本数据中获得见解。Python是一种通用且广泛使用的编程语言,它提供了多个库和工具来促进提取过程。_python提取pdf文件... [详细]
赞
踩
- 通过JetsonTX2NX的GPIO接口控制继电器非常简单。只需要连接继电器模块到正确的GPIO引脚上,安装JetsonGPIO库,编写Python脚本并运行即可。这个技巧可以帮助实现各种下位机控制应用。_agxxavier支持gpio吗a... [详细]
赞
踩
- 先在pip中安装pyinstaller验证是否成功,在cmd中首先进入python环境,然后测试是否可以importpyinstaller,注意是需要区分大小写的。打包py文件,首先在工程中右键需要打包的文件,选择copypath。然后在c... [详细]
赞
踩
- 源自:GiteeFlask是一个微型的Python开发的Web框架,基于WerkzeugWSGI工具箱和Jinja2模板引擎。Flask使用BSD授权。Flas..._最佳练手的flask项目最佳练手的flask项目源自:GiteeFlas... [详细]
赞
踩




