来1道并查集题目（森林c++）_在计算机的图论中,树是由n个节点组成,除了根节点,每个节点都有一个“父节点”。例

在计算机的图论中，树是由编号1到N的N个节点组成，除了根节点，每个节点都有一个“父节点”。例如下面是一个5个节点的树。

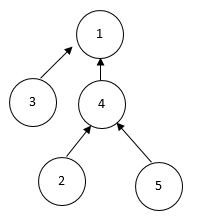
其中，2 、5号节点的父节点是4号节点，3、4号节点的父节点是1号节点， 1号节点是根节点，没有父节点。

这棵树的输入格式可以为：

共若干行：每行2个整数a,b，若a和b在同一颗树，输出0。否则，a所在的树的根连接到b所在的根，合并为一颗树，输出合并后树的高度。上图的树输入数据可以为：

2 4

5 4

3 1

2 3

图论中，还有森林概念，森林由多棵树组成。

现在每次加一个关系(a,b)后，输出相应的结果。本样例输出2 2 2 3 

输入格式

  第1行：2个正整数N，和M，分别表示节点数，和边数，范围在[1,1000000]。

  第2到M+1行：每行2个整数a,b。

【提示】数据比较大，需要使用scanf,printf。

输出格式

  M个数，表示每次加一个边(a,b)后，如果a和b不在同一棵树输出合并后的树高，否则输出0。

输入/输出例子1

输入：

10 7

10 9

2 8

6 6

1 5

5 4

10 2

1 2

输出：

2 2 0 2 3 3 4

样例解释

无

 好吧，并查集树，上代码！

/*
——————/′ ˉ/)
—————--/—-/
—————-/—-/
———--/′ˉ/'--'/′ˉ`•_
———-/'/--/—-/—--/¨ˉ\
——--('(———- ˉ~/'--')
———\————-'—--/
———-'\'————_-•′
————\———--(
————-\———-*/
#include<bits/stdc++.h>
using namespace std;
struct qi{
    int ro,hi;
}s[1000000];
int find_root(int i){
	int r=i;
    while(s[r].ro!=r){
        r=s[r].ro;
    }
    while(i!=r){
        int t=i;
        i=s[i].ro;
        s[t].ro=r;
    }
    return s[i].ro;
}
void init(int n,int m){
    for(int i=1;i<=n;i++){
        s[i].ro=i;
        s[i].hi=1;
    }
}
int main(){
    int n,m;
    scanf("%d%d",&n,&m);
    init(n,m);
    for(int i=0;i<m;i++){
    	int a,b;
        scanf("%d%d",&a,&b);
        int roa=find_root(a),rob=find_root(b);
        if(roa==rob) printf("0 ");
        else {
            s[rob].hi=max(s[rob].hi,s[roa].hi+1);
            printf("%d ",s[rob].hi);
            s[roa].ro=rob;
        }
    } 
    return 0;
}
 

稍微皮一下，嘻嘻。