Codeforces Round 919 (Div. 2) A - C 题解

A. Satisfying Constraints

题意：给你n个条件，给你两个数字a和x，如果a数字是1，让目标数字k>=x。如果a数字是2，让目标数字k<= x。如果a数字是3，让目标数字k!=x 。最后求出有多少数字符合条件。

题解：n很小，有很多种方法来做。我说一下我自己的吧，设两个边缘，一个Max ， 一个Min。控制好边缘以后将a == 3的数字存入数组，然后排序，看看其中多少个数字里，统计相减即可，有很多细节在代码里。

代码：

#include<bits/stdc++.h>
using namespace std ;
typedef long long ll ;
const int maxn = 1e6 + 7 ;
inline ll read(){
	ll x = 0 , f = 1;
	char c = getchar() ;
	while(c > '9' || c < '0'){
		if(c == '-')
			f = -1 ;
		c = getchar() ;
	}
	while(c >= '0' && c <= '9'){
		x = x * 10 + c - '0' ;
		c = getchar() ;
	}
	return x * f ;
}
ll t , n , m , a[maxn] , b[maxn] ;
void solve(){
	n = read() ;
	map < ll , ll > mp ;
	ll minn = 1 , maxx = 1e9 , cnt = 0 ;
	for(int i = 1 ; i <= n ; i ++){
		ll u , v ;
		u = read() ;
		v = read() ;
		if(u == 1){
			minn = max(minn , v) ;
		}
		if(u == 2){
			maxx = min(maxx , v) ;
		}
		if(u == 3){
			b[++ cnt] = v ;
		}
	}
	if(minn > maxx){
		cout << 0 << endl ;
		return ;
	}
	sort(b + 1 , b + cnt + 1) ;
	ll rt = -1 , Rt = -1 ;
	for(int i = 1 ; i <= cnt ; i ++){
		if(b[i] >= minn){
			rt = i ;
			break ;
		}
	}
	for(int i = cnt ; i >= 1 ; i --){
		if(b[i] <= maxx){
			Rt = i ;
			break ;
		}
	}
	if(rt == -1 || Rt == -1){
		cout << maxx - minn + 1 << endl ;
		return ;
	}
	else{
		cout << maxx - minn + 1 - (Rt - rt + 1) << endl ;
		return ;
	}
}
int main(){
	t = read() ;
	while(t --){
		solve() ;
	}
	return 0 ;
}

B. Summation Game

题意：给你n个数字，还有一个k一个x。有两个人，Alice和Bob。Alice最多可以删除k个数字，Bod最多可以将x个数字变成他的相反数。Alice想让结果最大，Bob想让最后的数字和尽量的小，两个人都用最优的策略。求最后的答案是多少。

题解：首先看Bob的操作，因为所有的数字都大于0，所以肯定是将更多的数字变成相反数答案会变到最小。那这个题就迎刃而解了，枚举() ，所有答案取最小值即可，当然需要用前缀和优化。

代码：

#include<bits/stdc++.h>
using namespace std ;
typedef long long ll ;
const int maxn = 1e6 + 7 ;
inline ll read(){
	ll x = 0 , f = 1;
	char c = getchar() ;
	while(c > '9' || c < '0'){
		if(c == '-')
			f = -1 ;
		c = getchar() ;
	}
	while(c >= '0' && c <= '9'){
		x = x * 10 + c - '0' ;
		c = getchar() ;
	}
	return x * f ;
}
ll t , n , m , k , a[maxn] , sum[maxn] , s[maxn] ;
void solve(){
	n = read() ;
	m = read() ;
	k = read() ;
	for(int i = 1 ; i <= n ; i ++){
		a[i] = read() ;
	}
	sort(a + 1 , a + n + 1) ;
	for(int i = 1 ; i <= n ; i ++){
		sum[i] = sum[i - 1] + a[i] ;
		s[i] = s[i - 1] - a[i] ;
	}
	ll ans = -LONG_LONG_MAX ;
	for(int i = n ; i >= n - m ; i --){
		ll res = sum[i] ;
		res += (s[i] - s[max(i - k , 0ll)]) * 2 ;
		ans = max(ans , res) ;
	}
	cout << ans << endl ;
}
int main(){
	t = read() ;
	while(t --){
		solve() ;
	}
	return 0 ;
}

C. Partitioning the Array

题意：给你n个数字，你可以枚举k，将n个数字切成段数字段，k必须是n的因子，看看能否有一个m()，将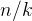段数字所有变成一样的。查询一共有多少个答案。

题解：一开始我想错了，想的是奇偶性，交了之后发现不对，想到了用gcd，很明显，分成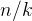段之后，每段数字相对应的数字（）的差的gcd必须大于1才能成立。那这道题就很简单了。复杂度O()

代码：

#include<bits/stdc++.h>
using namespace std ;
typedef long long ll ;
typedef pair < ll , ll > PII ;
const int maxn = 1e6 + 7 ;
inline ll read(){
	ll x = 0 , f = 1;
	char c = getchar() ;
	while(c > '9' || c < '0'){
		if(c == '-')
			f = -1 ;
		c = getchar() ;
	}
	while(c >= '0' && c <= '9'){
		x = x * 10 + c - '0' ;
		c = getchar() ;
	}
	return x * f ;
}
ll t , n , m , k , a[maxn] , b[maxn] , sum[maxn] , ji[maxn] , ou[maxn] ;
vector < PII > q ;
vector < ll > p ;
void solve(){
	n = read() ;
	for(ll i = 0 ; i <= n + 100 ; i ++){
		ji[i] = ou[i] = 0 ;
	}
	ll cnt = 0 , ans = 0 ;
	for(ll i = 1 ; i <= (ll)(sqrt(n)) ; i ++){
		if(n % i == 0){
			if(i == n / i){
				b[++ cnt] = i ;
			}
			else{
				b[++ cnt] = i ;
				b[++ cnt] = n / i ;
			}
		}
	}
	sort(b + 1 , b + cnt + 1) ;
	for(int i = 1 ; i <= n ; i ++){
		a[i] = read() ;
	}
	for(int i = 1 ; i <= cnt ; i ++){		
		ll gg = 0 ;
		for(int j = 1 ; j <= b[i] ; j ++){
			p.clear() ;
			for(int k = j ; k <= n ; k += b[i]){
				p.push_back(a[k]) ;
			}
			sort(p.begin() , p.end()) ;
			for(int i = 1 ; i < (int)p.size() ; i ++){
				gg = __gcd(gg , p[i] - p[i - 1]) ;
			}
		}
		if(gg != 1){
			ans ++ ;
		}
	}
	cout << ans << endl ;
}
int main(){
	t = read() ;
	while(t --){
		solve() ;
	}
	return 0 ;
}

总结下来这场比赛打的并不理想，可以发现关于将所有数字变成一样类似的题，都可以用gcd来解，或者是奇偶性。

喜欢作者的记得点赞收藏加关注哦~