Codeforces Round 919 (Div. 2) E. Counting Binary Strings

E. Counting Binary Strings

题意

定义一个字串 $s$ 为 $good$ 当且将当：$s$ 有且仅有 $1$ 个字符 ${}^{\prime }{1}^{\prime }$
请统计有多少个字符串：恰好有 $n$ 个 $good$ 的字串，且每个 $good$ 的字串长度都不大于 $k$

思路

先从贡献的角度考虑一个串 $s$ 有多少个 $good$ 的字串， 从官方题解的例子来看：每一个 $1$ 的贡献都是其两边的 $0$ 的数量 $+1$ 的乘积，$+1$ 是因为 $1$ 本身也要算进去。

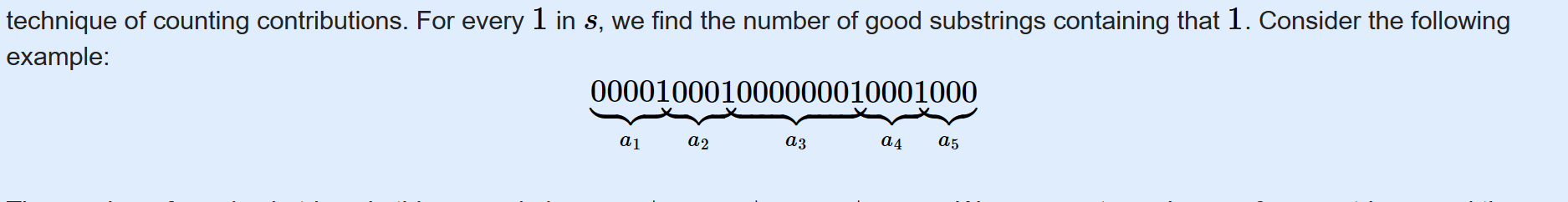
那么上面这个串的 $good$ 字串数量就是：$a_1{a}_2+a_2{a}_3+a_3{a}_4+a_4{a}_5$
可以发现总的数量就是数组 $a$ 中相邻两个元素的乘积，并且我们如果在末尾加上一个新的元素 $a_j$ ，是不会影响前面的结果的，而且可以直接使用前面的结果来计算新的数量。那么我们可以考虑 $DP$ ：
令 $d{p}_{i,j}$ 表示和恰好为 $i$ ，且 $a$ 的最后一个元素是 $j$ 的字符串数量。那么我们可以写出转移方程：

$dp[i][j]={\sum }_{p=1}^{min(\lfloor \frac{i}{j}\rfloor ,k-j+1)}dp[i-p\cdot j][p]$

意思就是枚举最后一位为 $j$，再枚举倒数第二位为 $p$，注意 $p\cdot j\le i$ 且 $p+j-1\le k$（$good$串长度不能超过 $k$）

初始化要令 $\forall j\in [1,k]，dp[0][j]=1$，这是由于如果后面某一个和 $i$，其最后两个元素乘起来刚好是 $i$ 的情况，也就是对应 $a$ 长度只有 $2$，即 $s=00000001$ 或 $s=100000$ 这种情况。

这样子对于每一个 $i$ 和 $j$，我们枚举 $p$ 最多到 $\lfloor \frac{i}{j}\rfloor$ ，所有 $j$ 求和起来就是 $\lfloor \frac{i}{1}\rfloor +\lfloor \frac{i}{2}\rfloor +...+\lfloor \frac{i}{i}\rfloor =O(i\log i)$。
最终的时间复杂度就是 $O(n\sum i\log i)=O(n^2\log n)$

#include<bits/stdc++.h>
#define fore(i,l,r)	for(int i=(int)(l);i<(int)(r);++i)
#define fi first
#define se second
#define endl '\n'
#define ull unsigned long long
#define ALL(v) v.begin(), v.end()
#define Debug(x, ed) std::cerr << #x << " = " << x << ed;

const int INF=0x3f3f3f3e;
const long long INFLL=1e18;

typedef long long ll;

template<class T>
constexpr T power(T a, ll b){
    T res = 1;
    while(b){
        if(b&1) res = res * a;
        a = a * a;
        b >>= 1;
    }
    return res;
}

constexpr ll mul(ll a,ll b,ll mod){ //快速乘，避免两个long long相乘取模溢出
    ll res = a * b - ll(1.L * a * b / mod) * mod;
    res %= mod;
    if(res < 0) res += mod; //误差
    return res;
}

template<ll P>
struct MLL{
    ll x;
    constexpr MLL() = default;
    constexpr MLL(ll x) : x(norm(x % getMod())) {}

    static ll Mod;
    constexpr static ll getMod(){
       if(P > 0) return P;
       return Mod;
    }

    constexpr static void setMod(int _Mod){
       Mod = _Mod;
    }
    constexpr ll norm(ll x) const{
       if(x < 0){
           x += getMod();
       }
       if(x >= getMod()){
           x -= getMod();
       }
       return x;
    }
    constexpr ll val() const{
       return x;
    }
    explicit constexpr operator ll() const{ 
       return x; //将结构体显示转换为ll类型： ll res = static_cast<ll>(OBJ)
    }
    constexpr MLL operator -() const{ //负号，等价于加上Mod
       MLL res;
       res.x = norm(getMod() - x);
       return res;
    }
    constexpr MLL inv() const{
       assert(x != 0);
       return power(*this, getMod() - 2); //用费马小定理求逆
    }
    constexpr MLL& operator *= (MLL rhs) & { //& 表示“this”指针不能指向一个临时对象或const对象
       x = mul(x, rhs.x, getMod()); //该函数只能被一个左值调用
       return *this;
    }
    constexpr MLL& operator += (MLL rhs) & {
       x = norm(x + rhs.x);
       return *this;
    }
    constexpr MLL& operator -= (MLL rhs) & {
       x = norm(x - rhs.x);
       return *this;
    }
    constexpr MLL& operator /= (MLL rhs) & {
       return *this *= rhs.inv();
    }
    friend constexpr MLL operator * (MLL lhs, MLL rhs){
       MLL res = lhs;
       res *= rhs;
       return res;
    }
    friend constexpr MLL operator + (MLL lhs, MLL rhs){
       MLL res = lhs;
       res += rhs;
       return res;
    }
    friend constexpr MLL operator - (MLL lhs, MLL rhs){
       MLL res = lhs;
       res -= rhs;
       return res;
    }
    friend constexpr MLL operator / (MLL lhs, MLL rhs){
       MLL res = lhs;
       res /= rhs;
       return res;
    }
    friend constexpr std::istream& operator >> (std::istream& is, MLL& a){
       ll v;
       is >> v;
       a = MLL(v);
       return is;
    }
    friend constexpr std::ostream& operator << (std::ostream& os, MLL& a){
       return os << a.val();
    }
    friend constexpr bool operator == (MLL lhs, MLL rhs){
       return lhs.val() == rhs.val();
    }
    friend constexpr bool operator != (MLL lhs, MLL rhs){
       return lhs.val() != rhs.val();
    }
};

const ll mod = 998244353;
using Z = MLL<mod>;

int main(){
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    std::cout.tie(nullptr);
    int t;
    std::cin>>t;
    while(t--){
        int n,k;
        std::cin>>n>>k;
        std::vector<std::vector<Z>> dp(n+1, std::vector<Z>(k+1, 0));
        fore(i,1,k+1) dp[0][i] = 1;
        Z ans = 0;
        fore(i,1,n+1){
            fore(j,1,k+1)
                fore(p,1,std::min(i/j, k-j+1) + 1)
                    dp[i][j] += dp[i - p*j][p];
        }
        fore(j,1,k+1) ans += dp[n][j];
        std::cout<<ans<<endl;
    }
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148