python实现选择排序_python选择排序

排序算法：
python实现基数排序
python实现归并排序
python实现交换排序
python实现选择排序
python实现插入排序

简单选择排序
基本思想：假设排序表为L[1…n]，第i趟排序即从L[i…n]中选择关键字最小的的元素与L[i]交换，每一趟排序可以确定一个元素的最终位置，则经过n-1趟排序可以使得整个排序表有序。

def SelectionSort(A):
    le=len(A)
    for i in range(le):#遍历次数
        for j in range(i+1,le):#查找待排序序列中的最小元素并交换
            if A[i]>A[j]:
                A[i],A[j]=A[j],A[i]
    print(A)
tes=[2,4,5,46,34,56,345,34,454]
SelectionSort(tes)#[2, 4, 5, 34, 34, 46, 56, 345, 454]
1
2
3
4
5
6
7
8
9

空间效率：仅使用常数个辅助单元，因此空间效率为O(1)
时间效率：O(n²)
它是一个不稳定的排序算法。

堆排序
堆排序是一种树形选择排序方法，在排序过程中，将L[1…n]看作一棵完全二叉树的顺序存储结构，利用完全二叉树中双亲结点和孩子结点之间的内在关系，在当前无序区中选择关键字最大（或最小）的元素。
堆的定义：
n个关键字序列L[1…n]称为堆，当且仅当该序列满足：
1）L[i]<=L[2i]且L[i]<=L[2i+1](小根堆）
2) L[i]>=L[2i]且L[i]>=L[2i+1](大根堆）
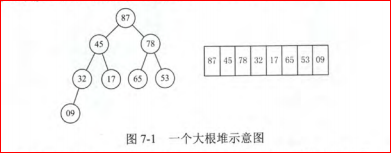堆排序的关键是构造初始堆，对初始序列建堆，就是一个反复筛选的过程。n个结点的完全二叉树，最后一个结点是n//2个节点的孩子。对n//2个节点为根的子树筛选（对于大根堆，若根结点的关键字小鱼左右子女中关键字较大者，则交换），使该子树成为堆。之后向前依次对各节点（n//2~1）为根的子树进行筛选，看该结点是否大于其左右子节点的值，若不是，则将左右子结点中较大值与之交换，交换后可能会破坏下一级的堆，于是继续采用上述方法构造下一级的堆，直到以该结点为根的子树构成堆为止。
同时，堆也支持删除和插入操作。由于堆顶元素为最大值或者最小值，删除堆顶元素时，先将堆的最后一个元素与堆顶元素交换，由于此时堆得性质被破坏，需对此时的根结点进行向下调整操作。
对堆进行插入操作时，先将新结点放在堆的末端，再对这个结点执行向上调整操作。

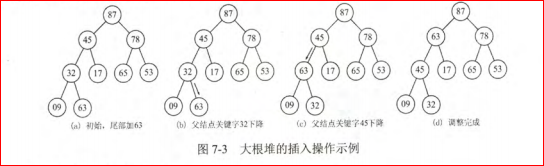
# 实现一个最大堆
class MaxHeap(object):
    """
    实现一个大顶堆
    """

    def __init__(self):
        self.array = [] # 用一个数组存放堆中元素

    def heapify(self, array):
        """
        对传入的数组进行堆化
        """
        for a in array:
            self.push(a)
        return self.array

    def get_size(self):
        """
        返回堆的大小
        """
        return len(self.array)

    def _parent(self, index):
        """
        返回某个节点的父节点
        """
        if index == 0:
            raise Exception('Index 0 has no parent')
        return int((index - 1) / 2)

    def _left_child(self, index):
        """
        返回左孩子节点的索引
        """
        return index * 2 + 1

    def _right_child(self, index):
        """
        返回右边孩子节点的索引
        """
        return index * 2 + 2

    def _shift_up(self, k):
        """
        节点上移动，将当前节点与其父亲节点比较大小，如果比父亲节点大，
        则交换其位置，重复只执行上述过程，直到当前节点比父亲节点小。
        """
        while k > 0 and self.array[self._parent(k)] < self.array[k]:
            # 交换节点与父节点的值
            self.array[self._parent(k)], self.array[k] = self.array[k], self.array[self._parent(k)]
            k = self._parent(k)

    def _shift_down(self, k):
        """
        节点下移动, 当前节点与它左右孩子中最大的节点交换位置
        """
        while self._left_child(k) < self.get_size():
            choose_index = self._left_child(k)  # 左孩子的索引
            # 先比较左右孩子的大小，选择较大的那个孩子再与父亲节点进行比较
            if choose_index + 1 < self.get_size() and self.array[choose_index + 1] > self.array[choose_index]:
                choose_index = self._right_child(k)
            if self.array[choose_index] <= self.array[k]:  # 如果最大的孩子比父亲节点小，退出循环
                break
            # 否则父亲节点和最大的子节点交换位置
            self.array[choose_index], self.array[k] = self.array[k], self.array[choose_index]
            k = choose_index  # 进行下次循环

    def push(self, value):
        """
        添加一个元素后，需要对堆重新进行堆化，具体过程就是对堆尾元素执行上移操作；
        """
        self.array.append(value)
        self._shift_up(self.get_size() - 1)  # 相当于对堆进行重新堆化

    def pop(self):
        """
        返回堆顶元素，将堆顶元素和堆最后一个元素交换，
        然后返回最后一个元素，最后对堆顶元素进行下沉操作（重新堆化）
        """
        ret = self.find_max()
        self.array[0], self.array[self.get_size() - 1] = self.array[self.get_size() - 1], self.array[0]
        self.array.pop(-1)  # 删除最后一个元素
        self._shift_down(0)
        return ret

    def find_max(self):
        """
        查看堆中的最大值
        """
        if self.array:
            return self.array[0]
        else:
            raise Exception('Empty heap has no value')

# 测试我们实现的大顶堆
test = [12, 11, 10, 9, 6, 7, 8, 13]
max_heap = MaxHeap()
print(max_heap.heapify(test)) # 对一个数组执行堆化
print(max_heap.pop()) # 弹出堆顶元素
print(max_heap.array) 
max_heap.push(14) # 推入一个元素
print(max_heap.array)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104

空间效率：仅使用常数个辅助单元，因此空间效率为O(1)
时间效率：O(nlog2 N)
它是一种不稳定的排序算法