- 1曲线生成 | 图解三次样条曲线生成原理(附ROS C++/Python/Matlab仿真)
- 2函数判断素数_函数训练之素数判断(预处理篇)
- 3asp.net解决高并发的方案
- 4Maven 教程(11)— Maven远程仓库的各种配置_maven 配置远程仓库
- 5linux cp 目录 斜杠,用cp命令拷贝文件,源目录后带不带斜杠的区别
- 6<HarmonyOS第一课>ArkTS开发语言介绍--闯关习题答案_下面哪些装饰器可以用于管理自定义组件中变量的状态
- 7spring boot 集成 pagehelper_springboot集成pagehelper
- 8Codeforces科学刷题指南,一图一表便够了_codeforces刷题顺序
- 9Windows Server【开机启动和任务计划程序】实现服务器重启后项目自启动(Windows Server 任务计划程序无法执行问题处理)_windows server 开机启动项
- 10OutOfMemoryError(内存溢出错误)可能的原因和解决方法_outofmemoryerror怎么解决
用javascript分类刷leetcode3.动态规划(图文视频讲解)
赞
踩
什么是动态规划
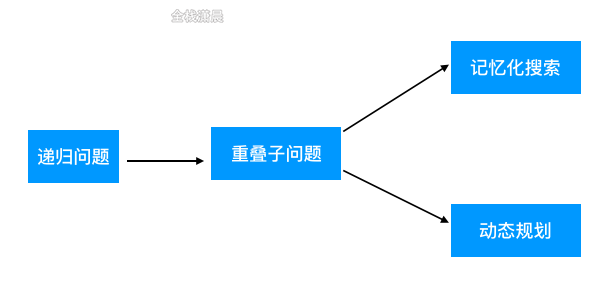
动态规划,英文:Dynamic Programming,简称DP,将问题分解为互相重叠的子问题,通过反复求解子问题来解决原问题就是动态规划,如果某一问题有很多重叠子问题,使用动态规划来解是比较有效的。
求解动态规划的核心问题是穷举,但是这类问题穷举有点特别,因为这类问题存在「重叠子问题」,如果暴力穷举的话效率会极其低下。动态规划问题一定会具备「最优子结构」,才能通过子问题的最值得到原问题的最值。另外,虽然动态规划的核心思想就是穷举求最值,但是问题可以千变万化,穷举所有可行解其实并不是一件容易的事,只有列出**正确的「状态转移方程」**才能正确地穷举。重叠子问题、最优子结构、状态转移方程就是动态规划三要素
动态规划和其他算法的区别
- 动态规划和分治的区别:动态规划和分治都有最优子结构 ,但是分治的子问题不重叠
- 动态规划和贪心的区别:动态规划中每一个状态一定是由上一个状态推导出来的,这一点就区分于贪心,贪心没有状态推导,而是从局部直接选最优解,所以它永远是局部最优,但是全局的解不一定是最优的。
- 动态规划和递归的区别:递归和回溯可能存在非常多的重复计算,动态规划可以用递归加记忆化的方式减少不必要的重复计算
动态规划的解题方法
- 递归+记忆化(自顶向下)
- 动态规划(自底向上)
解动态规划题目的步骤
- 根据重叠子问题定义状态
- 寻找最优子结构推导状态转移方程
- 确定dp初始状态
- 确定输出值
斐波那契的动态规划的解题思路
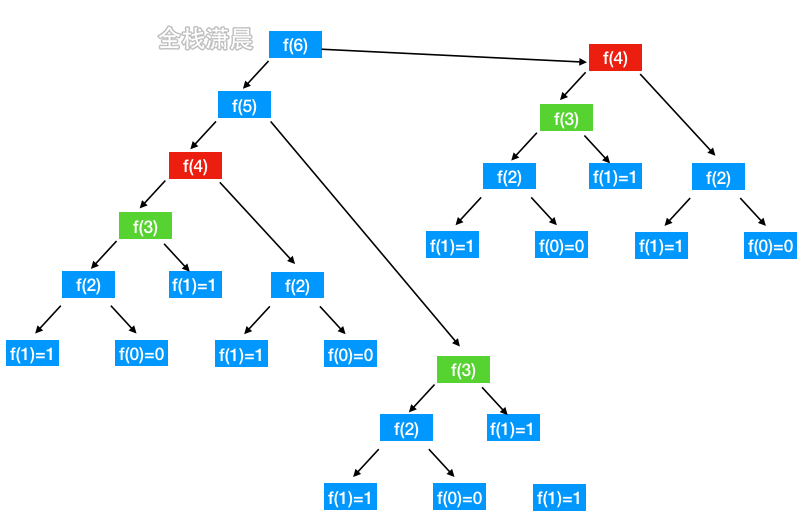
暴力递归
//暴力递归复杂度O(2^n)
var fib = function (N) {
if (N == 0) return 0;
if (N == 1) return 1;
return fib(N - 1) + fib(N - 2);
};
- 1
- 2
- 3
- 4
- 5
- 6
递归 + 记忆化
var fib = function (n) {
const memo = {}; // 对已算出的结果进行缓存
const helper = (x) => {
if (memo[x]) return memo[x];
if (x == 0) return 0;
if (x == 1) return 1;
memo[x] = helper(x - 1) + helper(x - 2);
return memo[x];
};
return helper(n);
};
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
动态规划
const fib = (n) => {
if (n <= 1) return n;
const dp = [0, 1];
for (let i = 2; i <= n; i++) {
//自底向上计算每个状态
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
};
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
滚动数组优化
const fib = (n) => {
if (n <= 1) return n;
//滚动数组 dp[i]只和dp[i-1]、dp[i-2]相关,只维护长度为2的滚动数组,不断替换数组元素
const dp = [0, 1];
let sum = null;
for (let i = 2; i <= n; i++) {
sum = dp[0] + dp[1];
dp[0] = dp[1];
dp[1] = sum;
}
return sum;
};
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
动态规划 + 降维,(降维能减少空间复杂度,但不利于程序的扩展)
var fib = function (N) {
if (N <= 1) {
return N;
}
let prev2 = 0;
let prev1 = 1;
let result = 0;
for (let i = 2; i <= N; i++) {
result = prev1 + prev2; //直接用两个变量就行
prev2 = prev1;
prev1 = result;
}
return result;
};
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
10. 正则表达式匹配(hard)
给你一个字符串 s 和一个字符规律 p,请你来实现一个支持 ‘.’ 和 ‘*’ 的正则表达式匹配。
‘.’ 匹配任意单个字符
‘*’ 匹配零个或多个前面的那一个元素
所谓匹配,是要涵盖 整个 字符串 s的,而不是部分字符串。示例 1:
输入:s = “aa”, p = “a”
输出:false
解释:“a” 无法匹配 “aa” 整个字符串。
示例 2:输入:s = “aa”, p = “a*”
输出:true
解释:因为 ‘*’ 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 ‘a’。因此,字符串 “aa” 可被视为 ‘a’ 重复了一次。
示例 3:输入:s = “ab”, p = “."
输出:true
解释:".” 表示可匹配零个或多个(‘*’)任意字符(‘.’)。提示:
1 <= s.length <= 20
1 <= p.length <= 30
s 只包含从 a-z 的小写字母。
p 只包含从 a-z 的小写字母,以及字符 . 和 *。
保证每次出现字符 * 时,前面都匹配到有效的字符
方法1.动态规划
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-N8qCVMiV-1670395631060)(https://xiaochen1024.com/20211118130839.png)]
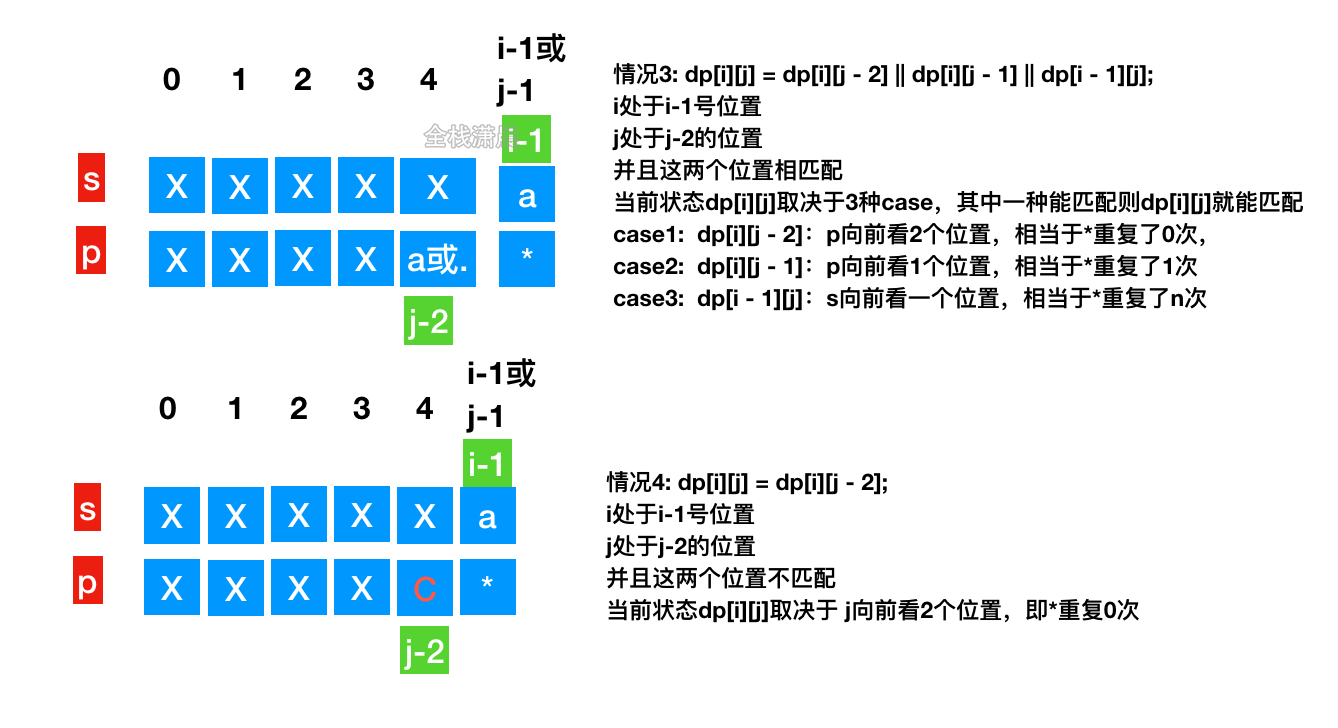
- 思路:
dp[i][j]表示 s 的前 i 个字符能否和p的前j个字符匹配,分为四种情况,看图 - 复杂度:时间复杂度
O(mn),m,n分别是字符串s和p的长度,需要嵌套循环s和p。空间复杂度O(mn),dp数组所占的空间
js:
//dp[i][j]表示s的前i个字符能否和p的前j个字符匹配 const isMatch = (s, p) => { if (s == null || p == null) return false;//极端情况 s和p都是空 返回false const sLen = s.length, pLen = p.length; const dp = new Array(sLen + 1);//因为位置是从0开始的,第0个位置是空字符串 所以初始化长度是sLen + 1 for (let i = 0; i < dp.length; i++) {//初始化dp数组 dp[i] = new Array(pLen + 1).fill(false); // 将项默认为false } // base case s和p第0个位置是匹配的 dp[0][0] = true; for (let j = 1; j < pLen + 1; j++) {//初始化dp的第一列,此时s的位置是0 //情况1:如果p的第j-1个位置是*,则j的状态等于j-2的状态 //例如:s='' p='a*' 相当于p向前看2个位置如果匹配,则*相当于重复0个字符 if (p[j - 1] == "*") dp[0][j] = dp[0][j - 2]; } // 迭代 for (let i = 1; i < sLen + 1; i++) { for (let j = 1; j < pLen + 1; j++) { //情况2:如果s和p当前字符是相等的 或者p当前位置是. 则当前的dp[i][j] 可由dp[i - 1][j - 1]转移过来 //当前位置相匹配,则s和p都向前看一位 如果前面所有字符相匹配 则当前位置前面的所有字符也匹配 //例如:s='XXXa' p='XXX.' 或者 s='XXXa' p='XXXa' if (s[i - 1] == p[j - 1] || p[j - 1] == ".") { dp[i][j] = dp[i - 1][j - 1]; } else if (p[j - 1] == "*") {//情况3:进入当前字符不匹配的分支 如果当前p是* 则有可能会匹配 //s当前位置和p前一个位置相同 或者p前一个位置等于. 则有三种可能 //其中一种情况能匹配 则当前位置的状态也能匹配 //dp[i][j - 2]:p向前看2个位置,相当于*重复了0次, //dp[i][j - 1]:p向前看1个位置,相当于*重复了1次 //dp[i - 1][j]:s向前看一个位置,相当于*重复了n次 //例如 s='XXXa' p='XXXa*' if (s[i - 1] == p[j - 2] || p[j - 2] == ".") { dp[i][j] = dp[i][j - 2] || dp[i][j - 1] || dp[i - 1][j]; } else { //情况4:s当前位置和p前2个位置不匹配,则相当于*重复了0次 //例如 s='XXXb' p='XXXa*' 当前位置的状态和p向前看2个位置的状态相同 dp[i][j] = dp[i][j - 2]; } } } } return dp[sLen][pLen]; // 长为sLen的s串 是否匹配 长为pLen的p串 };
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
72. 编辑距离 (hard)
给你两个单词 word1 和 word2, 请返回将 word1 转换成 word2 所使用的最少操作数 。
你可以对一个单词进行如下三种操作:
插入一个字符
删除一个字符
替换一个字符示例 1:
输入:word1 = “horse”, word2 = “ros”
输出:3
解释:
horse -> rorse (将 ‘h’ 替换为 ‘r’)
rorse -> rose (删除 ‘r’)
rose -> ros (删除 ‘e’)
示例 2:输入:word1 = “intention”, word2 = “execution”
输出:5
解释:
intention -> inention (删除 ‘t’)
inention -> enention (将 ‘i’ 替换为 ‘e’)
enention -> exention (将 ‘n’ 替换为 ‘x’)
exention -> exection (将 ‘n’ 替换为 ‘c’)
exection -> execution (插入 ‘u’)提示:
0 <= word1.length, word2.length <= 500
word1 和 word2 由小写英文字母组成
方法1.动态规划


- 思路:
dp[i][j]表示word1前i个字符和word2前j个字符的最少编辑距离。- 如果
word1[i-1] === word2[j-1],说明最后一个字符不用操作,此时dp[i][j] = dp[i-1][j-1],即此时的最小操作数和word1和word2都减少一个字符的最小编辑数相同 - 如果
word1[i-1] !== word2[j-1],则分为三种情况- word1删除最后一个字符,状态转移成
dp[i-1][j],即dp[i][j] = dp[i-1][j] + 1,+1指删除操作 - word1在最后加上一个字符,状态转移成
dp[i][j-1],即dp[i][j] = dp[i][j-1] + 1,+1指增加操作 - word1替换最后一个字符,状态转移成
dp[i-1][j-1],即dp[i] [j] = dp[i-1] [j-1] + 1,+1指替换操作
- word1删除最后一个字符,状态转移成
- 如果
- 复杂度:时间复杂度是
O(mn),m是word1的长度,n是word2的长度。空间复杂度是O(mn),需要用m * n大小的二维数字存储状态。
Js:
const minDistance = (word1, word2) => { let dp = Array.from(Array(word1.length + 1), () => Array(word2.length + 1).fill(0)); //初始化数组,word1前i个字符最少需要i次操作,比如i次删除变成word2 for (let i = 1; i <= word1.length; i++) { dp[i][0] = i; } //初始化数组,word2前i个字符最少需要i次操作,比如j次插入变成word1 for (let j = 1; j <= word2.length; j++) { dp[0][j] = j; } for (let i = 1; i <= word1.length; i++) { //循环word1和word2 for (let j = 1; j <= word2.length; j++) { if (word1[i - 1] === word2[j - 1]) { //如果word1[i-1] === word2[j-1],说明最后一个字符不用操作。 dp[i][j] = dp[i - 1][j - 1]; } else { //dp[i-1][j] + 1:对应删除 //dp[i][j-1] + 1:对应新增 // dp[i-1][j-1] + 1:对应替换操作 dp[i][j] = Math.min(dp[i - 1][j] + 1, dp[i][j - 1] + 1, dp[i - 1][j - 1] + 1); } } } return dp[word1.length][word2.length]; };
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
64. 最小路径和 (medium)
给定一个包含非负整数的 m x n 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明:每次只能向下或者向右移动一步。
示例 1:
输入:grid = [[1,3,1],[1,5,1],[4,2,1]]
输出:7
解释:因为路径 1→3→1→1→1 的总和最小。
示例 2:输入:grid = [[1,2,3],[4,5,6]]
输出:12提示:
m == grid.length
n == grid[i].length
1 <= m, n <= 200
0 <= grid[i][j] <= 100
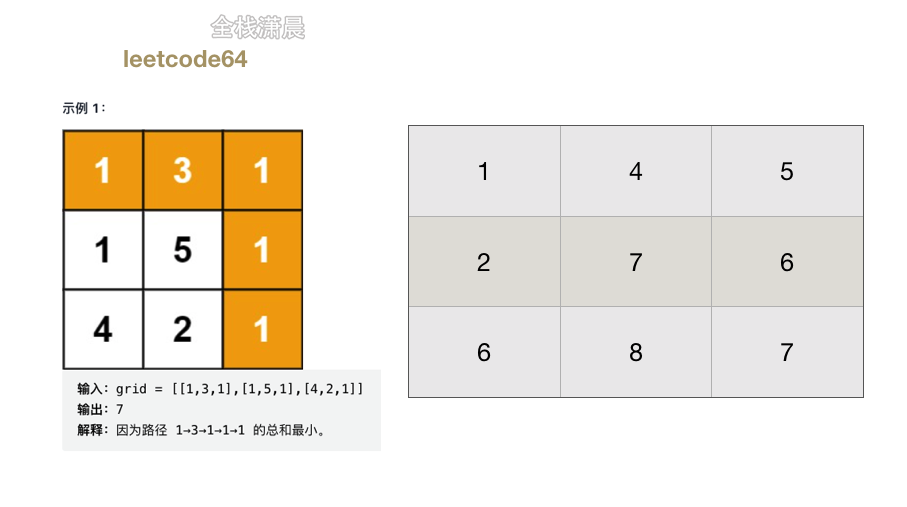
- 思路:
dp[i][j]表示从矩阵左上角到(i,j)这个网格对应的最小路径和,只要从上到下,从左到右遍历网格,当前最小路径和就是当前的数值加上上面和左边左小的。 - 复杂度:时间复杂度
O(mn),m、n分别是矩阵的长和宽。空间复杂度如果原地修改是O(1),如果新建dp数组就是O(mn)
js:
var minPathSum = function(dp) {
let row = dp.length, col = dp[0].length
for(let i = 1; i < row; i++)//初始化第一列
dp[i][0] += dp[i - 1][0]
for(let j = 1; j < col; j++)//初始化第一行
dp[0][j] += dp[0][j - 1]
for(let i = 1; i < row; i++)
for(let j = 1; j < col; j++)
dp[i][j] += Math.min(dp[i - 1][j], dp[i][j - 1])//取上面和左边最小的
return dp[row - 1][col - 1]
};
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
322. 零钱兑换 (medium)
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。
你可以认为每种硬币的数量是无限的。
示例 1:
输入:coins = [1, 2, 5], amount = 11
输出:3
解释:11 = 5 + 5 + 1
示例 2:输入:coins = [2], amount = 3
输出:-1
示例 3:输入:coins = [1], amount = 0
输出:0提示:
1 <= coins.length <= 12
1 <= coins[i] <= 231 - 1
0 <= amount <= 104
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-rLpfc4nZ-1670395631072)(https://xiaochen1024.com/20211118130836.png)]
不能用贪心做,反例,coins=[1, 3, 5, 6, 7],amount=30,用贪心先用最大的面额7,在用2个1,4 * 7 + 2 * 1 = 30,但是我们用5个6,5 * 6 = 30 就能用最少的硬币兑换完成
方法1.动态规划
- 思路:
dp[i]表示兑换面额i所需要的最少硬币,因为硬币无限,所以可以自底向上计算dp[i],对于dp[0~i]的每个状态,循环coins数组,寻找可以兑换的组合,用i面额减去当前硬币价值,dp[i-coin]在加上一个硬币数就是dp[i],最后取最小值就是答案,状态转移方程就是dp[i] = Math.min(dp[i], dp[i - coin] + 1); - 复杂度分析:时间复杂度是O(sn),s是兑换金额,n是硬币数组长度,一共需要计算s个状态,每个状态需要遍历n个面额来转移状态。空间复杂度是
O(s),也就是dp数组的长度
Js:
var coinChange = function (coins, amount) { let dp = new Array(amount + 1).fill(Infinity);//初始化dp数组 dp[0] = 0;//面额0只需要0个硬币兑换 for (let i = 1; i <= amount; i++) {//循环面额 for (let coin of coins) {//循环硬币数组 if (i - coin >= 0) {//当面额大于硬币价值时 //dp[i - coin]: 当前面额i减当前硬币价值所需要的最少硬币 //dp[i] 可由 dp[i - coin] + 1 转换而来 dp[i] = Math.min(dp[i], dp[i - coin] + 1); } } } return dp[amount] === Infinity ? -1 : dp[amount];//如果dp[amount] === Infinity,则无法兑换 };
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
509. 斐波那契数(easy)
斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是:
F(0) = 0,F(1) = 1
F(n) = F(n - 1) + F(n - 2),其中 n > 1
给定 n ,请计算 F(n) 。示例 1:
输入:n = 2
输出:1
解释:F(2) = F(1) + F(0) = 1 + 0 = 1
示例 2:输入:n = 3
输出:2
解释:F(3) = F(2) + F(1) = 1 + 1 = 2
示例 3:输入:n = 4
输出:3
解释:F(4) = F(3) + F(2) = 2 + 1 = 3提示:
0 <= n <= 30
方法1.动态规划
- 思路:自底而上的动态规划
- 复杂度分析:时间复杂度
O(n),空间复杂度O(1)
Js:
var fib = function (N) {
if (N <= 1) {
return N;
}
let prev2 = 0;
let prev1 = 1;
let result = 0;
for (let i = 2; i <= N; i++) {
result = prev1 + prev2;
prev2 = prev1;
prev1 = result;
}
return result;
};
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
312. 戳气球 (hard)
有 n 个气球,编号为0 到 n - 1,每个气球上都标有一个数字,这些数字存在数组 nums 中。
现在要求你戳破所有的气球。戳破第 i 个气球,你可以获得 nums[i - 1] * nums[i] * nums[i + 1] 枚硬币。 这里的 i - 1 和 i + 1 代表和 i 相邻的两个气球的序号。如果 i - 1或 i + 1 超出了数组的边界,那么就当它是一个数字为 1 的气球。
求所能获得硬币的最大数量。
示例 1:
输入:nums = [3,1,5,8]
输出:167
解释:
nums = [3,1,5,8] --> [3,5,8] --> [3,8] --> [8] --> []
coins = 315 + 358 + 138 + 181 = 167
示例 2:输入:nums = [1,5]
输出:10提示:
n == nums.length
1 <= n <= 300
0 <= nums[i] <= 100
方法1:动态规划
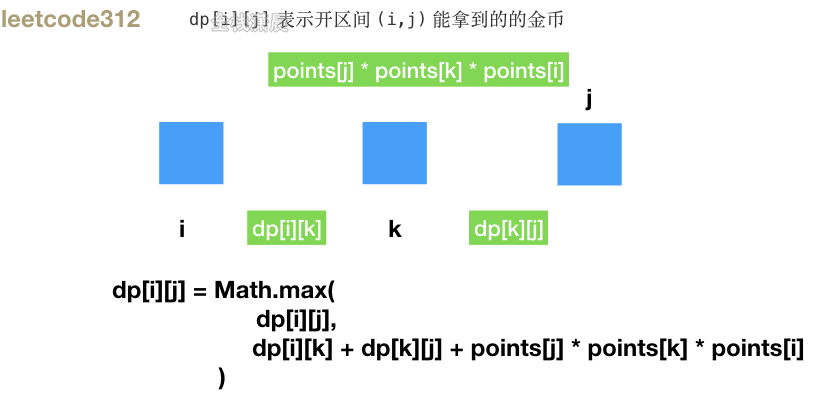
- 思路:
dp[i][j]表示开区间(i,j)能拿到的的金币,k是这个区间 最后一个 被戳爆的气球,枚举i和j,遍历所有区间,i-j能获得的最大数量的金币等于 戳破当前的气球获得的金钱加上之前i-k、k-j区间中已经获得的金币 - 复杂度:时间复杂度
O(n^3),n是气球的数量,三层遍历。空间复杂度O(n^2),dp数组的空间。
js:
var maxCoins = function (nums) { const n = nums.length; let points = [1, ...nums, 1]; //两边添加虚拟气球 const dp = Array.from(Array(n + 2), () => Array(n + 2).fill(0)); //dp数组初始化 //自底向上转移状态 for (let i = n; i >= 0; i--) { //i不断减小 for (let j = i + 1; j < n + 2; j++) { //j不断扩大 for (let k = i + 1; k < j; k++) { //枚举k在i和j中的所有可能 //i-j能获得的最大数量的金币等于 戳破当前的气球获得的金钱加上之前i-k,k-j区间中已经获得的金币 dp[i][j] = Math.max( //挑战最大值 dp[i][j], dp[i][k] + dp[k][j] + points[j] * points[k] * points[i] ); } } } return dp[0][n + 1]; };
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
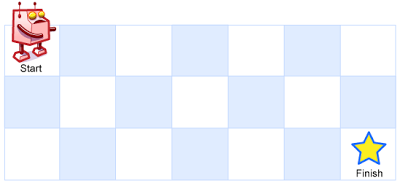
62. 不同路径 (medium)
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
示例 1:
输入:m = 3, n = 7
输出:28
示例 2:输入:m = 3, n = 2
输出:3
解释:
从左上角开始,总共有 3 条路径可以到达右下角。
- 向右 -> 向下 -> 向下
- 向下 -> 向下 -> 向右
- 向下 -> 向右 -> 向下
示例 3:
输入:m = 7, n = 3
输出:28
示例 4:输入:m = 3, n = 3
输出:6提示:
1 <= m, n <= 100
题目数据保证答案小于等于 2 * 109
方法1.动态规划
- 思路:由于在每个位置只能向下或者向右, 所以每个坐标的路径和等于上一行相同位置和上一列相同位置不同路径的总和,状态转移方程:
f[i][j] = f[i - 1][j] + f[i][j - 1]; - 复杂度:时间复杂度
O(mn)。空间复杂度O(mn),优化后O(n)
js:
var uniquePaths = function (m, n) { const f = new Array(m).fill(0).map(() => new Array(n).fill(0)); //初始dp数组 for (let i = 0; i < m; i++) { //初始化列 f[i][0] = 1; } for (let j = 0; j < n; j++) { //初始化行 f[0][j] = 1; } for (let i = 1; i < m; i++) { for (let j = 1; j < n; j++) { f[i][j] = f[i - 1][j] + f[i][j - 1]; } } return f[m - 1][n - 1]; }; //状态压缩 var uniquePaths = function (m, n) { let cur = new Array(n).fill(1); for (let i = 1; i < m; i++) { for (let r = 1; r < n; r++) { cur[r] = cur[r - 1] + cur[r]; } } return cur[n - 1]; };
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
0-1背包问题
0-1背包问题指的是有n个物品和容量为j的背包,weight数组中记录了n个物品的重量,位置i的物品重量是weight[i],value数组中记录了n个物品的价值,位置i的物品价值是vales[i],每个物品只能放一次到背包中,问将那些物品装入背包,使背包的价值最大。
举例:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-0UQccsaJ-1670395631078)(https://xiaochen1024.com/20211118193828.png)]
我们用动态规划的方式来做
-
状态定义:
dp[i][j]表示从前i个物品里任意取,放进容量为j的背包,价值总和最大是多少 -
状态转移方程:
dp[i][j] = max(dp[i - 1][j],dp[i - 1][j - weight[i]] + value[i]); 每个物品有放入背包和不放入背包两种情况- 当
j - weight[i]<0:表示装不下i号元素了,不放入背包,此时dp[i][j] = dp[i - 1][j],dp[i] [j]取决于前i-1中的物品装入容量为j的背包中的最大价值 - 当
j - weight[i]>=0:可以选择放入或者不放入背包。
放入背包则:dp[i][j] = dp[i - 1][j - weight[i]] + value[i],dp[i - 1][j - weight[i]]表示i-1中的物品装入容量为j-weight[i]的背包中的最大价值,然后在加上放入的物品的价值value[i]就可以将状态转移到dp[i][j]。
不放入背包则:dp[i][j] = dp[i - 1] [j],在这两种情况中取较大者。
- 当
-
初始化dp数组:
dp[i][0]表示背包的容积为0,则背包的价值一定是0,dp[0][j]表示第0号物品放入背包之后背包的价值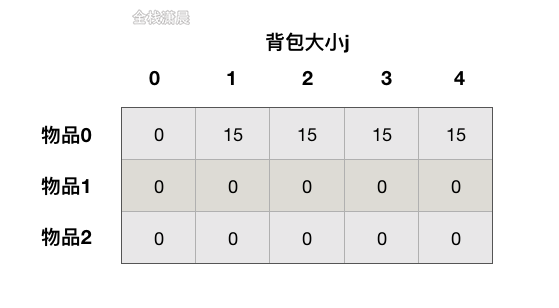
-
最终需要返回值:就是dp数组的最后一行的最后一列
循环完成之后的dp数组如下图
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ZMHmcFuo-1670395631082)(https://xiaochen1024.com/20211118130844.png)]
js:
function testWeightBagProblem(wight, value, size) { const len = wight.length, dp = Array.from({ length: len + 1 }).map(//初始化dp数组 () => Array(size + 1).fill(0) ); //注意我们让i从1开始,因为我们有时会用到i - 1,为了防止数组越界 //所以dp数组在初始化的时候,长度是wight.length+1 for (let i = 1; i <= len; i++) { for (let j = 0; j <= size; j++) { //因为weight的长度是wight.length+1,并且物品下标从1开始,所以这里i要减1 if (wight[i - 1] <= j) { dp[i][j] = Math.max( dp[i - 1][j], value[i - 1] + dp[i - 1][j - wight[i - 1]] ) } else { dp[i][j] = dp[i - 1][j]; } } } return dp[len][size]; } function test() { console.log(testWeightBagProblem([1, 3, 4], [15, 20, 30], 4)); } test();
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
状态压缩
根据状态转移方程dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]),第i行只与第i-1行状态相关,所以我们可以用滚动数组进行状态压缩,其次我们注意到,j只与j前面的状态相关,所以只用一个数组从后向前计算状态就可以了。
function testWeightBagProblem2(wight, value, size) {
const len = wight.length,
dp = Array(size + 1).fill(0);
for (let i = 1; i <= len; i++) {
//从后向前计算,如果从前向后的话,最新的值会覆盖老的值,导致计算结果不正确
//dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - wight[i - 1]] + value[i - 1])
for (let j = size; j >= wight[i - 1]; j--) {
dp[j] = Math.max(dp[j], dp[j - wight[i - 1]] + value[i - 1] );
}
}
return dp[size];
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
416. 分割等和子集 (medium)
给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
示例 1:
输入:nums = [1,5,11,5]
输出:true
解释:数组可以分割成 [1, 5, 5] 和 [11] 。
示例 2:输入:nums = [1,2,3,5]
输出:false
解释:数组不能分割成两个元素和相等的子集。提示:
1 <= nums.length <= 200
1 <= nums[i] <= 100
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-2X7fEMBi-1670395631084)(https://xiaochen1024.com/20211118130846.png)]
- 思路:本题可以看成是0-1背包问题,给一个可装载重量为
sum / 2的背包和 N 个物品,每个物品的重量记录在 nums 数组中,问是否在一种装法,能够恰好将背包装满?dp[i][j]表示前i个物品是否能装满容积为j的背包,当dp[i][j]为true时表示恰好可以装满。每个数都有放入背包和不放入两种情况,分析方法和0-1背包问题一样。 - 复杂度:时间复杂度
O(n*sum),n是nums数组长度,sum是nums数组元素的和。空间复杂度O(n * sum),状态压缩之后是O(sum)
js:
//可以看成是0-1背包问题,给一个可装载重量为 sum / 2 的背包和 N 个物品, //每个物品的重量记录在 nums 数组中,问是否在一种装法,能够恰好将背包装满? var canPartition = function (nums) { let sum = 0 let n = nums.length for (let i = 0; i < n; i++) { sum += nums[i] } if (sum % 2 !== 0) {//如果是奇数,那么分割不了,直接返回false return false } sum = sum / 2 //dp[i][j]表示前i个物品是否能装满容积为j的背包,当dp[i][j]为true时表示恰好可以装满 //最后求的是 dp[n][sum] 表示前n个物品能否把容量为sum的背包恰好装满 //dp数组长度是n+1,而且是二维数组,第一维表示物品的索引,第二个维度表示背包大小 let dp = new Array(n + 1).fill(0).map(() => new Array(sum + 1).fill(false)) //dp数组初始化,dp[..][0] = true表示背包容量为0,这时候就已经装满了, //dp[0][..] = false 表示没有物品,肯定装不满 for (let i = 0; i <= n; i++) { dp[i][0] = true } for (let i = 1; i <= n; i++) {//i从1开始遍历防止取dp[i - 1][j]的时候数组越界 let num = nums[i - 1] //j从1开始,j为0的情况已经在dp数组初始化的时候完成了 for (let j = 1; j <= sum; j++) { if (j - num < 0) {//背包容量不足 不能放入背包 dp[i][j] = dp[i - 1][j];//dp[i][j]取决于前i-1个物品是否能前好装满j的容量 } else { //dp[i - 1][j]表示不装入第i个物品 //dp[i - 1][j-num]表示装入第i个,此时需要向前看前i - 1是否能装满j-num //和背包的区别,这里只是返回true和false 表示能否装满,不用计算价值 dp[i][j] = dp[i - 1][j] || dp[i - 1][j - num]; } } } return dp[n][sum] }; //状态转移方程 F[i, target] = F[i - 1, target] || F[i - 1, target - nums[i]] //第 n 行的状态只依赖于第 n-1 行的状态 //状态压缩 var canPartition = function (nums) { let sum = nums.reduce((acc, num) => acc + num, 0); if (sum % 2) { return false; } sum = sum / 2; const dp = Array.from({ length: sum + 1 }).fill(false); dp[0] = true; for (let i = 1; i <= nums.length; i++) { //从后向前计算,如果从前向后的话,最新的值会覆盖老的值,导致计算结果不正确 for (let j = sum; j > 0; j--) { dp[j] = dp[j] || (j - nums[i] >= 0 && dp[j - nums[i]]); } } return dp[sum]; };
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
63. 不同路径 II(medium)
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish”)。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?
网格中的障碍物和空位置分别用 1 和 0 来表示。
示例 1:
输入:obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出:2
解释:3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径:
- 向右 -> 向右 -> 向下 -> 向下
- 向下 -> 向下 -> 向右 -> 向右
示例 2:
输入:obstacleGrid = [[0,1],[0,0]]
输出:1提示:
m == obstacleGrid.length
n == obstacleGrid[i].length
1 <= m, n <= 100
obstacleGrid[i][j] 为 0 或 1
方法1.动态规划
- 思路:和62题一样,区别就是遇到障碍直接返回0
- 复杂度:时间复杂度
O(mn),空间复杂度O(mn),状态压缩之后是o(n)
Js:
var uniquePathsWithObstacles = function (obstacleGrid) { const m = obstacleGrid.length; const n = obstacleGrid[0].length; const dp = Array(m) .fill() .map((item) => Array(n).fill(0)); //初始dp数组 for (let i = 0; i < m && obstacleGrid[i][0] === 0; ++i) { //初始列 dp[i][0] = 1; } for (let i = 0; i < n && obstacleGrid[0][i] === 0; ++i) { //初始行 dp[0][i] = 1; } for (let i = 1; i < m; ++i) { for (let j = 1; j < n; ++j) { //遇到障碍直接返回0 dp[i][j] = obstacleGrid[i][j] === 1 ? 0 : dp[i - 1][j] + dp[i][j - 1]; } } return dp[m - 1][n - 1]; }; //状态压缩 var uniquePathsWithObstacles = function (obstacleGrid) { let m = obstacleGrid.length; let n = obstacleGrid[0].length; let dp = Array(n).fill(0); //用0填充,因为现在有障碍物,当前dp数组元素的值还和obstacleGrid[i][j]有关 dp[0] = 1; //第一列 暂时用1填充 for (let i = 0; i < m; i++) { for (let j = 0; j < n; j++) { if (obstacleGrid[i][j] == 1) { //注意条件,遇到障碍物dp[j]就变成0,这里包含了第一列的情况 dp[j] = 0; } else if (j > 0) { //只有当j>0 不是第一列了才能取到j - 1 dp[j] += dp[j - 1]; } } } return dp[n - 1]; };
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
343. 整数拆分 (medium)
给定一个正整数 n ,将其拆分为 k 个 正整数 的和( k >= 2 ),并使这些整数的乘积最大化。
返回 你可以获得的最大乘积 。
示例 1:
输入: n = 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1。
示例 2:输入: n = 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。提示:
2 <= n <= 58

- 思路:
dp[i]为正整数i拆分之后的最大乘积,循环数字n,对每个数字进行拆分,取最大的乘积,状态转移方程:dp[i] = Math.max(dp[i], dp[i - j] * j, (i - j) * j),j*(i-j)表示把i拆分为j和i-j两个数相乘,j * dp[i-j]表示把i拆分成j和继续把(i-j)这个数拆分,取(i-j)拆分结果中的最大乘积与j相乘 - 复杂度:时间复杂度
O(n^2),两层循环。空间复杂度O(n),dp数组的空间
js:
var integerBreak = function (n) {
//dp[i]为正整数i拆分之后的最大乘积
let dp = new Array(n + 1).fill(0);
dp[2] = 1;
for (let i = 3; i <= n; i++) {
for (let j = 1; j < i; j++) {
//j*(i-j)表示把i拆分为j和i-j两个数相乘
//j*dp[i-j]表示把i拆分成j和继续把(i-j)这个数拆分,取(i-j)拆分结果中的最大乘积与j相乘
dp[i] = Math.max(dp[i], dp[i - j] * j, (i - j) * j);
}
}
return dp[n];
};
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
视频讲解:传送门
- 通过前面的文章我们可以知道基于区块链开发一个DApp,而DApp结合了智能合约和用户界面(客户端),那客户端是如何与区块链进行连接交互的、如何调用智能合约的、如何发送一个交易到区块链、如何获取区块链上的数据,这就是本文要介绍的web3.js... [详细]
赞
踩
- JavaScriptUIComponentsforBuildingFast,FlexibleApplicationsWithWijmo,spendmoretimeonyourapplication'scorefunctionalitybyt... [详细]
赞
踩
- CSS颜色与背景颜色color属性背景background属性1.背景颜色background-color2.背景图像background-image3.背景图像平铺方式background-repeat4.固定/滚动背景图像backgro... [详细]
赞
踩
- OD,全称(OutsourcingDispacth)模式,目前华为和德科联合招聘的简称。华为社招基本都是OD招聘,17级以下都是OD模式(13-17)。_华为od机试-2023真题-考点分类华为od机试-2023真题-考点分类华为OD机考:... [详细]
赞
踩
- 2DJavascript游戏引擎列表AkihabaraLincense:GPL2/MITAkihabara是用于创建8/16位图游戏的js库和工具集合。它通过使用HTML5Canvas实现。支持GoogleChrome,Saf_jsgame... [详细]
赞
踩
- 使用arcgisjavascriptapi4.x以basetilelayer方式加载天地图wgs84(wkid:4326)坐标系。提示:(下述三个文件放同一个文件夹下)arcgisjavascriptapi4.x加载天地图wgs84(wki... [详细]
赞
踩
- behavior可选,定义滚动是立即的还是平滑的动画。auto:滚动行为由scroll-behavior的计算值决定。instant:滚动应该通过一次跳跃立刻发生。smooth:滚动应该是平滑的动画。【JavaScript】使用scroll... [详细]
赞
踩
- 继承是基于“类”的,在没有es6前,一的函数就充当了“类”的,构造函数的prototype上面的属性就等于实例的共享属性。javascript常见的继承方式继承是基于“类”的,在没有es6前,一个用来new的函数就充当了“类”的构造函数,构... [详细]
赞
踩
- 一款简单的Servlet+mysql+jsp的选课系统,主要有三大模块,管理员模块,教师模块,学生模块。管理员模块主要功能模块有系统管理,课程管理,教师管理,课表管理,学生管理;基于javaweb+mysql的jsp+servlet选课管理... [详细]
赞
踩
- article
[HTML]Web前端开发技术15(HTML5、CSS3、JavaScript )表格,bordercolorlight,frame,valign,rowspan,colspan——喵喵画网页
表格 表格 表格标记 表格标记-语法 表格属性设置 表格边框样式属性 表格单元格间距、单元格边距属性 表格水平对齐 设置表格行的属性 表格行的属性-设置 设置单元格的属性 设置单元格的属性-单元格跨行、列 表格嵌套课后练习网页标题:计算机报... [详细]赞
踩
- 篮球(5v5)比赛中每个球员拥有一个战斗力,每个队伍的所有球员战斗力之和为该队伍的总体战斗力。现有十个球员准备分为两队进行训练赛,教练希望两个队伍的战斗力差能够尽可能的小,以达到最佳训练效果。给出十个球员的战斗力,如果你是教练,你该如何分队... [详细]
赞
踩
- 10个篮球队员的战斗力(整数,范围[1,10000]),战斗力之间用空格分隔,如:10987654321。现有10个球员准备分为两队进行训练赛,教练希望2个队伍的战斗力差值能够尽可能的小,以达到最佳训练效果。篮球(5V5)比赛中,每个球员拥... [详细]
赞
踩
- i=2,将nums[2]和nums[0]交换位置,从nums[1]开始累乘。i=0,将nums[0]和nums[0]交换位置,从nums[1]开始累乘。i=1,将nums[1]和nums[0]交换位置,从nums[1]开始累乘。_除自身以外... [详细]
赞
踩
- 下面首先完全copy了Cocoas官网上的内容,这里主要是做个笔记,初学JS调用IOS原声代码遇到的问题官网地址:https://docs.cocos.com/creator/manual/zh/advanced-topics/oc-ref... [详细]
赞
踩
- JavaScript基础知识点大全,超详细解析。基础学习,一篇足以!_定义和取出浏览器对象javascript定义和取出浏览器对象javascript这里写自定义目录标题js基础一.JavaScript概述1.1JavaScript应用场景... [详细]
赞
踩
- 如果我们要使用本地的音频资源,在vue3中那么我们需要对资源的地址做一下处理。_javascript获取二进制流并播放javascript获取二进制流并播放一、接口设置//语音播放exportconstgetVoicePlay=(conte... [详细]
赞
踩
- 网页标题:三列自适应宽度网页标题:多行三列自适应宽度一级水平导航菜单:采用“无序列表+超链接”设计[HTML]Web前端开发技术12(HTML5、CSS3、JavaScript)——喵喵画网页希望你开心,希望你健康,希望你幸福,希望你点赞!... [详细]
赞
踩
- 好久没有写博客了,不是没有在学习新东西,是最近比较忙,没有总结。今天聊的话题是防止js篡改。javascript代码和需要编译的代码有一点不同是,网页上会直接请求js文件源码,而编译的语言运行时使用的是编译后的文件。即使这样,很多编译语言(... [详细]
赞
踩
- JavaScript-在父元素与子元素都绑定多个事件时执行顺序事件的执行顺序绝对是让人头疼的问题。当父元素与子元素都绑定了多个事件,且有的绑定在冒泡阶段、有的绑定在捕获阶段时,事件的触发顺序如何?如果你只关心这个问题,请直接下滑到3.绑定多... [详细]
赞
踩
- JavaScript-观察者模式(publish/subscribe)观察者模式又叫做发布订阅模式,它定义了一种一对多的关系,让多个观察者对象同时监听某一个主题对象,这个主题对象的状态发生改变时就会通知所有观察着对象。它是由两类对象组成,主... [详细]
赞
踩