MATLAB程序设计教程 第3版 第五章实验指导、思考练习答案（个人版）

注：本系列文章仅仅用于交流学习，杜绝作业抄袭

第一章：MATLAB程序设计教程 第3版 第一章实验指导、思考练习答案（个人版）-CSDN博客

第二章：MATLAB程序设计教程 第3版 第二章实验指导、思考练习答案（个人版）-CSDN博客

第三章：MATLAB程序设计教程 第3版 第三章实验指导、思考练习答案（个人版）-CSDN博客

第四章：MATLAB程序设计教程 第3版 第四章实验指导、思考练习答案（个人版）-CSDN博客

第五章：MATLAB程序设计教程 第3版 第五章实验指导、思考练习答案（个人版）-CSDN博客

第六章：MATLAB程序设计教程 第3版 第六章实验指导、思考练习答案（个人版）-CSDN博客

实验指导：

A=randn(10,5)

B=mean(A) %均值

C=std(A) %标准差

 

mx=max(max(A)) %最大元素

mn=min(min(A)) %最小元素

 

sm=sum(A,2) %每行元素和

sz=sum(sum(A)) %所有元素和

 

col_up=sort(A,1,'ascend')

row_down=sort(A,2,'descend')
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

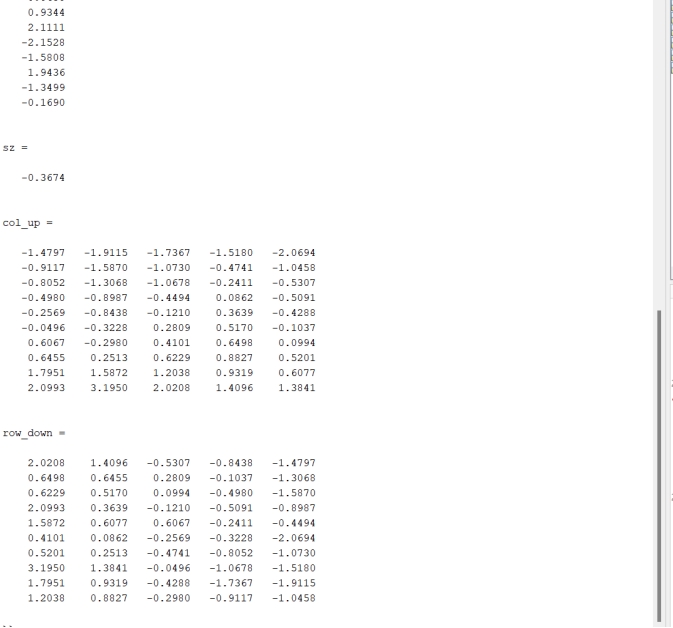
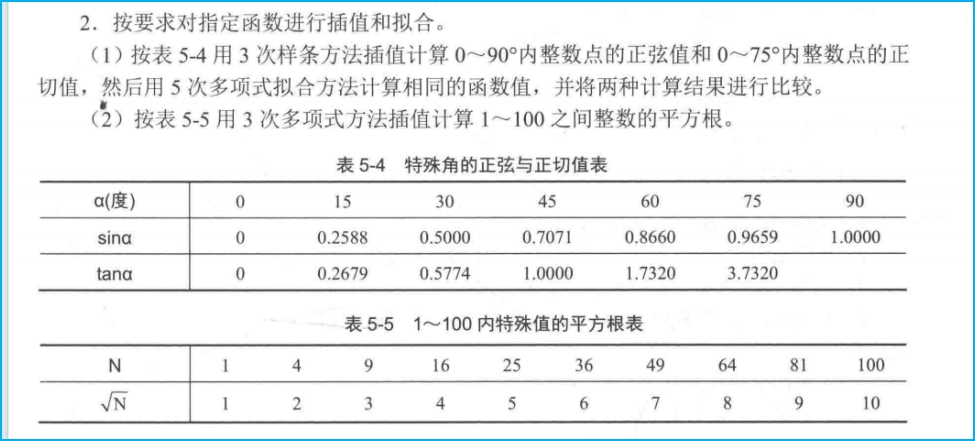
三次样条差值计算

h_sin=0:15:90;

t_sin=[0,0.2588,0.5000,0.7071,0.8660,0.9659,1.0000]';

h_tan=0:15:75;

t_tan=[0,0.2679,0.5774,1.0000,1.7320,3.7320]';

 

X_sin=0:1:90; %计算0-90°内整数点的正弦值

Y_sin=interp1(h_sin,t_sin,X_sin,"spline") %用三次样条差值计算

 

X_tan=0:1:75; %计算0-75°内整数点的正切值

Y_tan=interp1(h_tan,t_tan,X_tan,"spline") %用三次样条差值计算


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

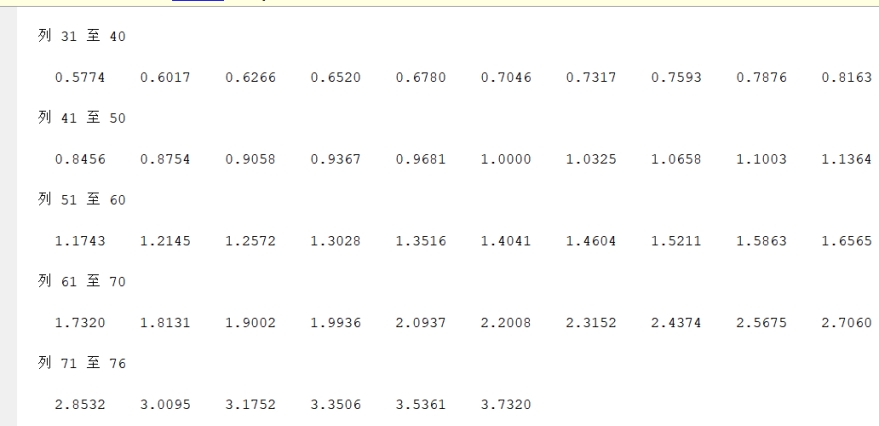
五次多项式拟合方法计算相同函数值

h_sin=0:15:90;

t_sin=[0,0.2588,0.5000,0.7071,0.8660,0.9659,1.0000];

p_sin = polyfit(h_sin,t_sin,5); %计算5次拟合多项式的系数

X_sin=0:1:90; %计算0-90°内整数点的正弦值

Y_sin=polyval(p_sin,X_sin)

 

h_tan=0:15:75;

t_tan=[0,0.2679,0.5774,1.0000,1.7320,3.7320]';

p_tan = polyfit(h_tan,t_tan,5); %计算5次拟合多项式的系数

X_tan=0:1:75; %计算0-75°内整数点的正切值

Y_tan=polyval(p_tan,X_tan)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

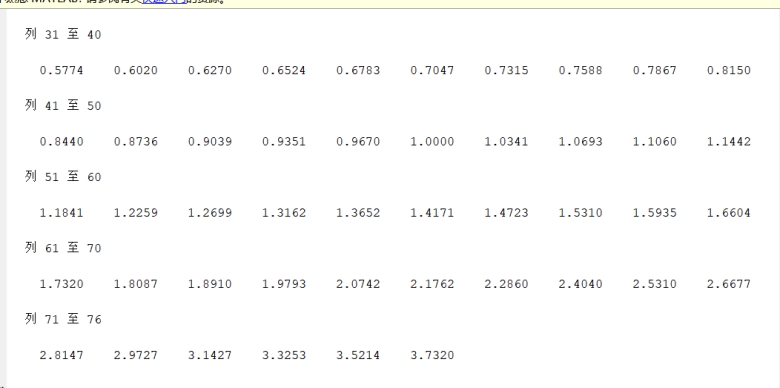
结果相近

三次多项式拟合方法计算1~100间整数平方根

N=[1,4,9,16,25,36,49,64,81,100];

N_genghao=[1,2,3,4,5,6,7,8,9,10];

p = polyfit(N,N_genghao,3); %计算5次拟合多项式的系数

X=0:1:100;

Y=polyval(p,X)
1
2
3
4
5
6
7
8
9

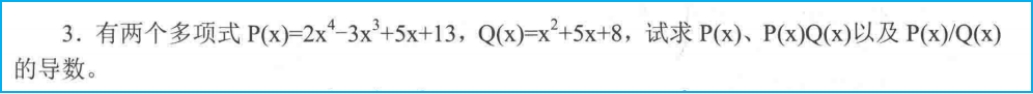
p = [2,-3,0,5,13];

q = [0,0,1,1,0];

 

ans1 = polyder(p)

ans2 = polyder(q)

ans3 = polyder(p,q)

[up,down] = polyder(p,q);

up

down
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

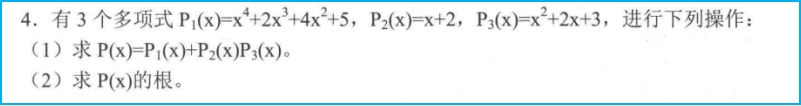
p1 = [2,2,4,0,5];

p2 = [0,0,0,1,2];

p3 = [0,0,1,1,3];

 

%第一问

ans1 = [0,0,0,0,2,2,4,0,5] + conv(p2,p3)

 

%第二问

ans2 = roots(ans1)

 

%第三问

A = [-1 1.2 -1.4;0.75 2 3.5;0 5 2.5];

ans3 = polyval(ans1,A)

%第四问

ans4 = polyvalm(ans1,A)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

思考练习：

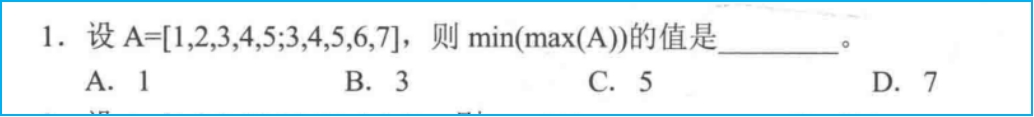
B

15 27 39 ；4 5 6

一维插值 interp1

polyfit，polyval

2x^2-1

x=roots([a,b,c]) polyval([a,b,c],x)

10

sum 函数：

sum 函数用于计算数组中元素的总和。

它接受一个数组作为输入，并返回数组中所有元素的总和。可以指定对某一维度求和。

cumsum 函数：

cumsum 函数用于计算数组元素的累积和。

它也接受一个数组作为输入，并返回一个数组，其中每个元素是原始数组从开头开始到当前位置的累积和。

数据插值（Interpolation）

数据插值是通过已知的数据点集合来估计新的数据点的值。它的目的是在给定的数据点之间寻找某种函数关系，以便在新的位置上近似估计数据点的值。

曲线拟合（Curve Fitting）

曲线拟合是通过拟合一个函数模型来近似描述一组数据点的整体趋势。它的目的是找到一个数学函数或曲线，以最好地描述数据点的分布。

共同点：

都是处理数据的方法，都用于近似估计数据点之间的值。

不同点：

数据插值更侧重于在已知数据点之间准确估算值，而曲线拟合更专注于找到一个函数模型来描述整体数据的趋势。

插值：数据插值主要关注在给定数据点间通过某种函数形式来准确估算新数据点的值。它试图通过插值函数在已知数据点之间进行精确地推断。

拟合：曲线拟合的目标是找到一个可以概括整个数据集趋势的函数模型，而不一定通过严格穿过每个已知数据点的方式。因此，它可能会忽略某些局部的细节，而专注于总体数据的大致趋势。

使用系数向量表示,如x^4+2x3+3x^2+4x+5，可以表示为[1,2,3,4,5]

a=rand(30000,1)

n=0

mean_a=mean(a)

std_a=std(a)

 

[max_num,weizhi1]=max(a)

[min_num,weizhi2]=min(a)

 

for ii=1:30000

if a(ii,1)>0.5

n=n+1;

end

end

percent_a=n/30000
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

A=rand(5,100);

P=100*A;

[Y,U1]=max(P,[],2); % 求每门功课的最高分、序号 

[X,U2]=min(P,[],2); % 求每门功课的最低分、序号 

Y

U1

X

U2

 

Z1=mean(P,2) % 求每门功课的平均值 

Z2=std(P,1,2) % 求每门功课的标准方差 

B1=cumsum(P); % 求五门功课的总成绩 

B=B1(5,:); 

[YZ,UZ1]=max(B,[],2) % 求总成绩的最高分 

[XZ,UZ2]=min(B,[],2) % 求总成绩的最低分 

zcj=-sort(-B,2)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

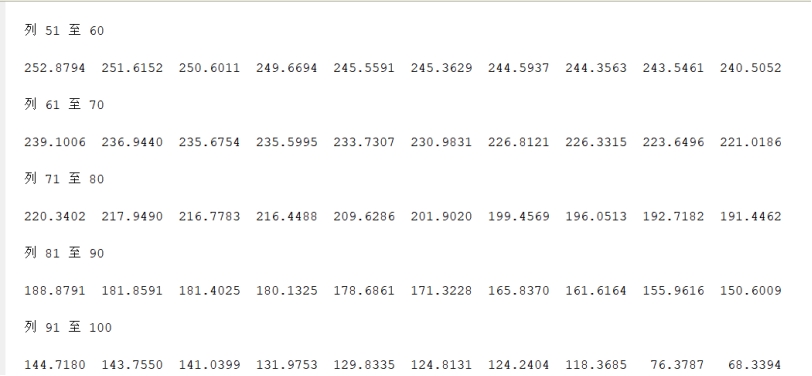
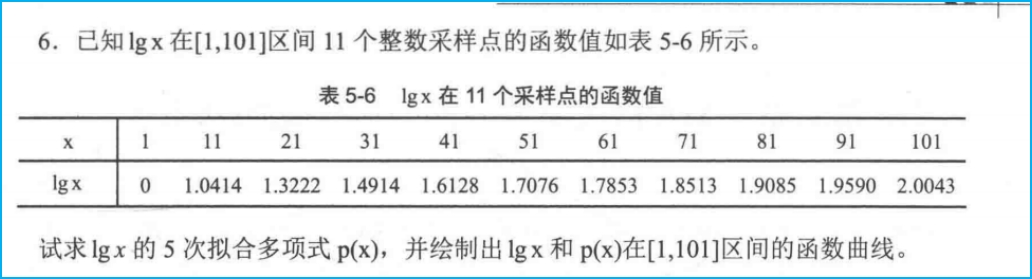
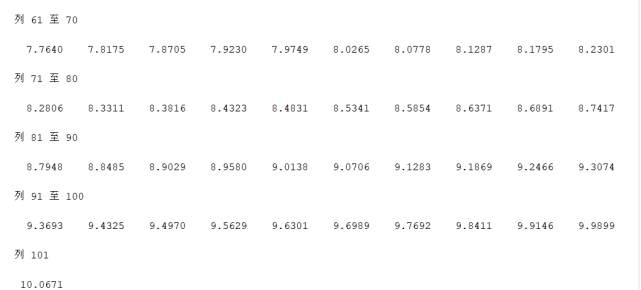
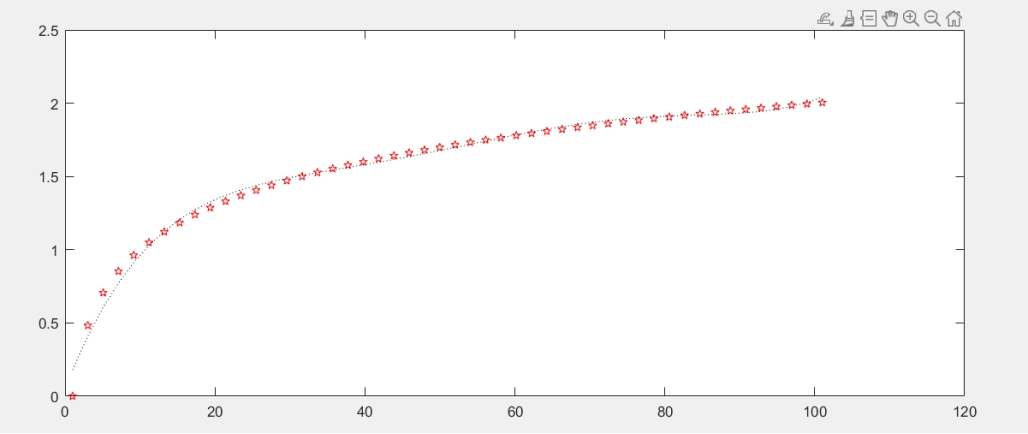
x=linspace(1,101,50);

y=log10(x);

P=polyfit(x,y,5)

y1=polyval(P,x);

plot(x,y,'rp',x,y1,'k:')
1
2
3
4
5
6
7
8
9