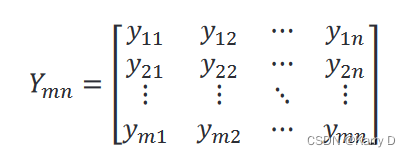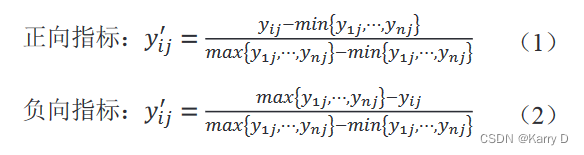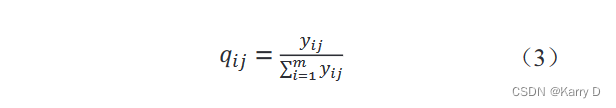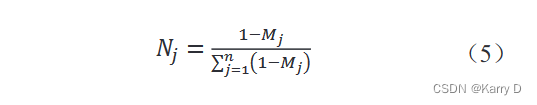- 1HBuilder-X 关闭eslint-vue 插件语法检查_hbuilder怎样去掉eslint
- 2详解Python多线程、多进程_python 接口线程
- 3分布式存储---哈希槽的概念
- 4docker常用命令汇总(40条)
- 55s换脸吴彦祖!爆红AI应用ZAO仍面临技术困境,你的“脸”被授权了吗?
- 6springboot项目elasticsearch7.x降版本到elasticsearch6.x实践_spring data elasticsearch 切换es版本
- 7微信小程序退出当前页面,关闭小程序_微信小程序关闭当前页面
- 8基于python-tensorflow的机器视觉学习手札 (1.4)图像处理篇-图像的空域、频域增强_空域卷积 频域增强
- 9SpringBoot集成ElasticSearch7进行增删查改_springboot es 7 delete
- 10Spring Authorization Server(授权服务器)授权处理流程原理过程_spring authorization server 原理
【综合评价分析】熵权算法确定权重 原理+完整MATLAB代码+详细注释+操作实列_熵权法matlab代码
赞
踩
【综合评价分析】熵权算法确定权重 原理+完整MATLAB代码+详细注释+操作实列
文章目录
采用熵权法进行客观权重计算的步骤为:
①根据评价等级对指标重要性进行打分,然后构建评价矩阵;
②将评价矩阵进行归一化处理,得到归一化评价矩阵;
③根据信息熵计算公式,计算各个指标 的信息熵;
④根据熵权计算公式,计算各个指标的客观权重值 。
1. 熵权法确定指标权重
(1)构造评价矩阵 Ymn
(2)评价矩阵标准化处理
采用线性比例变换法将评价矩阵进行初等变换,得到归一化矩阵进而解决不同指标值的同质化问题,其中正向指标与负向指标数值不同,但绝对值越大越好凹,例如计算指标的重要性与权重值的关系,权重值越大,则代表重要性越强,所以选择正向指标。
式中:yij ——评价矩阵原始值。
归一化:计算第 j 项指标下第 i 个样本值占该指标的比重 qij。
式中:m——总样本数。
(3)计算指标信息熵值 Mj
(4)计算各指标权重 Nj
2.完整代码
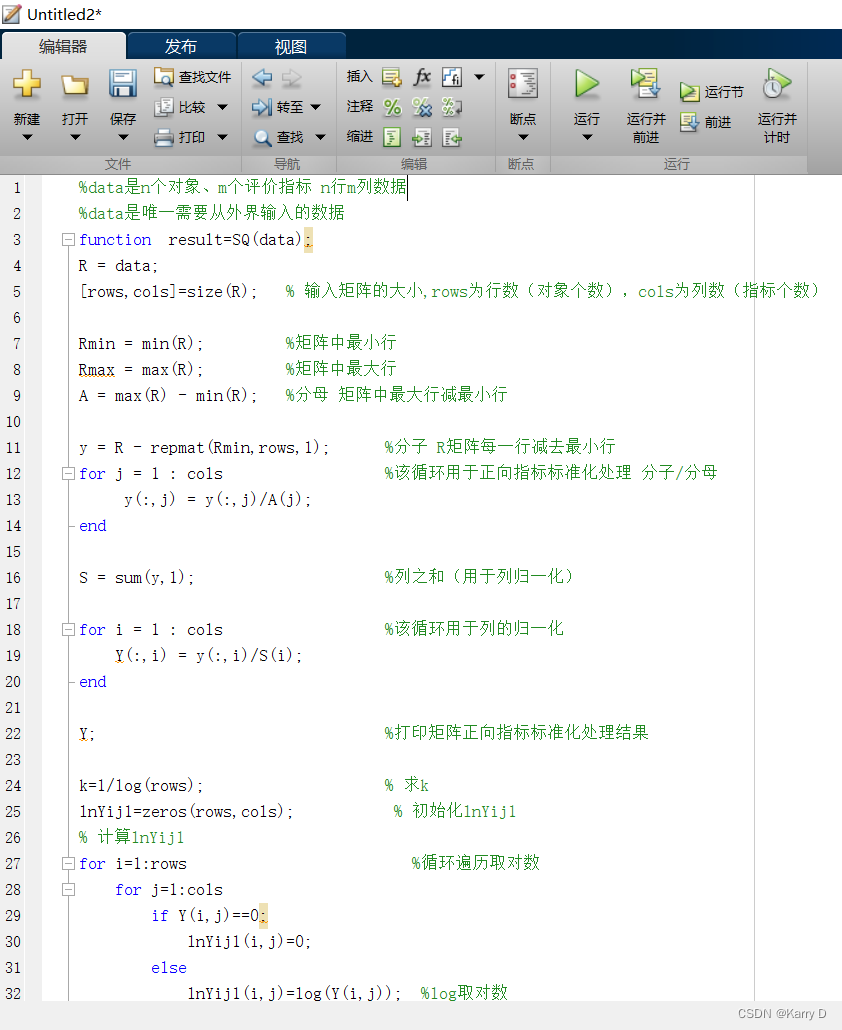
2.1 熵权法(正向化指标)
- %data是n个对象、m个评价指标 n行m列数据
- %data是唯一需要从外界输入的数据
- function result=SQ(data);
- R = data;
- [rows,cols]=size(R); % 输入矩阵的大小,rows为行数(对象个数),cols为列数(指标个数)
-
- Rmin = min(R); %矩阵中最小行
- Rmax = max(R); %矩阵中最大行
- A = max(R) - min(R); %分母 矩阵中最大行减最小行
-
- y = R - repmat(Rmin,rows,1); %分子 R矩阵每一行减去最小行
- for j = 1 : cols %该循环用于正向指标标准化处理 分子/分母
- y(:,j) = y(:,j)/A(j);
- end
-
- S = sum(y,1); %列之和(用于列归一化)
-
- for i = 1 : cols %该循环用于列的归一化
- Y(:,i) = y(:,i)/S(i);
- end
-
- Y; %打印矩阵正向指标标准化处理结果
-
- k=1/log(rows); % 求k
- lnYij1=zeros(rows,cols); % 初始化lnYij1
- % 计算lnYij1
- for i=1:rows %循环遍历取对数
- for j=1:cols
- if Y(i,j)==0;
- lnYij1(i,j)=0;
- else
- lnYij1(i,j)=log(Y(i,j)); %log取对数
- end
- end
- end
- ej1=-k*(sum(Y.*lnYij1,1)); % 计算正向指标标准化熵值ej1
-
- weights1=(1-ej1)/(cols-sum(ej1)); %正向指标权重weights1
-
-
- %结构体定义
- result(1).guiyihua = Y; %矩阵归一化结果赋给result
- result(1).shangzhi = ej1; %熵值赋给result
- result(1).weight = weights1; %权重赋给result

2.2熵权法(负向化指标)
- %data是n个对象、m个评价指标 n行m列数据
- %data是唯一需要从外界输入的数据
- function result=SQfuxiang(data);
- R = data;
- [rows,cols]=size(R); % 输入矩阵的大小,rows为行数(对象个数),cols为列数(指标个数)
-
- Rmin = min(R); %矩阵中最小行
- Rmax = max(R); %矩阵中最大行
- A = max(R) - min(R); %分母 矩阵中最大行减最小行
-
- y1 = repmat(Rmax,rows,1) - R; %分子 最大行减去R矩阵每一行
-
- for j = 1 : cols %该循环用于负向指标标准化处理 分子/分母
- y1(:,j) = y1(:,j)/A(j);
- end
- S = sum(y1,1); %列之和(用于列归一化)
- for i = 1 : cols %该循环用于列的归一化
- Y1(:,i) = y1(:,i)/S(i);
- end
- Y1; %打印矩阵负向指标标准化处理结果
-
- k=1/log(rows); % 求k
- lnYij2=zeros(rows,cols); % 初始化lnYij2
- % 计算lnYij1
- for i=1:rows %循环遍历取对数
- for j=1:cols
- if Y1(i,j)==0;
- lnYij2(i,j)=0;
- else
- lnYij2(i,j)=log(Y1(i,j)); %log取对数
- end
- end
- end
- ej2=-k*(sum(Y1.*lnYij2,1)); % 计算负向指标标准化熵值ej2
-
- weights2=(1-ej2)/(cols-sum(ej2)); %负向指标权重weights2
-
- %结构体定义
- result(1).guiyihua = Y1; %矩阵归一化结果赋给result
- result(1).shangzhi = ej2; %熵值赋给result
- result(1).weight = weights2; %权重赋给result

3.运行演示
3.1复制代码,建立函数
默认函数名保存即可
3.2 导入data数据集
%data是n个对象、m个评价指标 n行m列数据
%data是唯一需要从外界输入的数据
以下列子所用数据集为
5 3 7 3
6 7 6 4
9 4 7 5
10 6 9 2
6 4 8 6
7 2 8 3
5 4 5 3
9 5 9 2
3.3 运行指令
result=SQ(data)
result=SQfuxiang(data)
3.4 运行结果
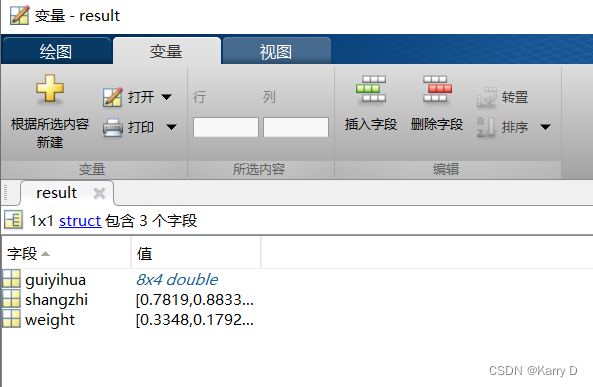
3.5 结构体 result变量
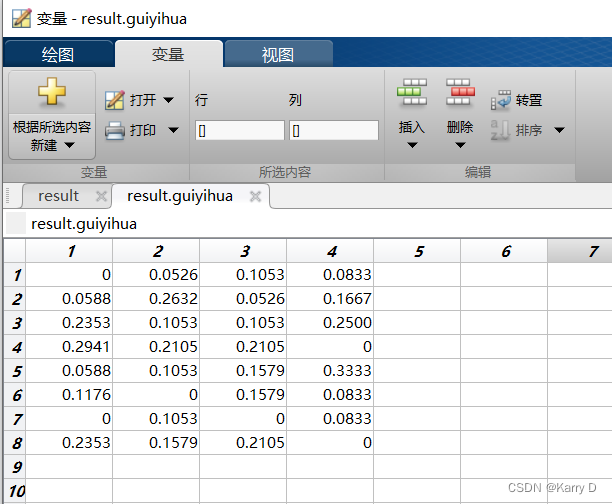
3.5.1 归一化
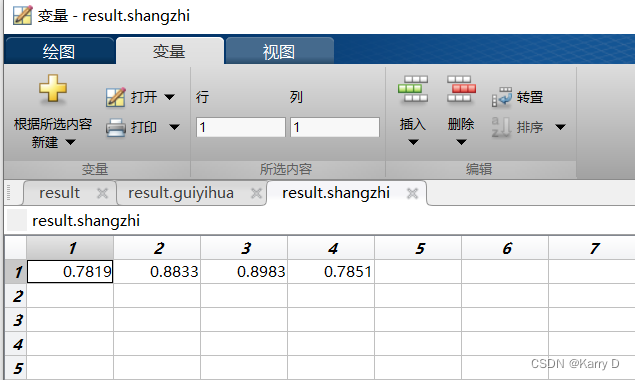
3.5.2 熵值
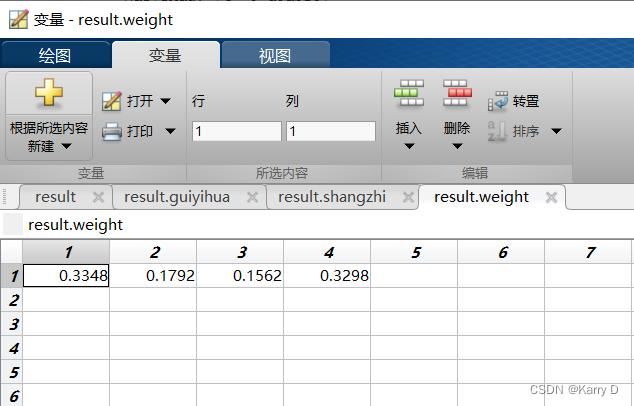
3.5.3 权重
3.6 熵权法(负向化指标)
运行指令换成
result=SQfuxiang(data)
即可
运行结果就不再过多赘述。
4.总结
采用熵权法进行客观权重计算的步骤为:
①根据评价等级对指标重要性进行打分,然后构建评价矩阵;
②将评价矩阵进行归一化处理,得到归一化评价矩阵;
③根据信息熵计算公式,计算各个指标 的信息熵;
④根据熵权计算公式,计算各个指标的客观权重值 。
本文包括了熵权算法法确定权重原理+完整MATLAB代码+详细注释+操作实列。
- D*算法(C++/MATLAB)_启发式值启发式值前言路径规划一直是机器人、自动驾驶、游戏开发等领域中的关键问题。D算法和A算法都是用于解决路径规划问题的重要算法。本文将深入介绍D算法的原理、实现和应用,并对比D算法与A*算法的区别。什么是... [详细]
赞
踩
- geneticalgorithm,美国Holland教授创立,基于达尔文进化论和孟德尔的遗传学说。遗传算法类比了生物界中自然选择、交叉、变异等自然进化方式,利用数码串类比染色体,通过选择、交叉、变异等遗传算子模拟生物的进化过程。_genet... [详细]
赞
踩
- 遗传算法(GeneticAlgorithm)是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法(进化算法),其基本原理是效仿生物界中的“物竞天择、适者生存”的演化法则。通俗来讲,... [详细]
赞
踩
- 设定的参数名(Param名)说明默认值交叉比例0.8算法中止的最大迭代次数100种群规模20变异概率0.2当适应度函数达到设定的值时算法中止当超过StallGenLimit代适应度函数为改善时,算法中止50。_matlab中ga函数用法ma... [详细]
赞
踩
- matlab----GA遗传算法_matlab遗传算法工具箱ga函数matlab遗传算法工具箱ga函数1.GA的调用:2.例:当N=10时函数为:functionf=lbw(x)ifx(1)>30||x(1)<-30||x(2)... [详细]
赞
踩
- •遗传算法(GeneticAlgorithm,GA)是由美国J.Holland教授于1975年在专著《自然界和人工系统的适应性》中首先提出。_matlabgamatlabga遗传算法的简单学习记录。目录一·优化问题二·群体智能优化算法思想三... [详细]
赞
踩
- 本文介绍了如何使用MATLAB实现遗传算法。遗传算法是一种模拟自然界生物进化机制的优化算法,它通过模拟自然选择、交叉和变异等操作来寻找问题的最优解。遗传算法通常包括以下步骤:定义问题的目标函数和约束条件,以及变量的编码方式。生成初始种群,即... [详细]
赞
踩
- matlabappdesigner系列-仪器仪表3-旋钮,示例:模拟收音机调频matlabappdesigner系列-仪器仪表3-旋钮旋钮,同过旋转显示特定的值示例:模拟收音机调频操作步骤:1)将旋钮、标签按钮拖拽到画布上,将标签文字修改为... [详细]
赞
踩
- 点击鼠标左键绘制对应光谱图像,点击鼠标中键暂停绘制,直到下一次点击鼠标中键再继续绘制。matlab实现点击图像绘制相应像素点的光谱曲线点击鼠标左键绘制对应光谱图像,点击鼠标中键暂停绘制,直到下一次点击鼠标中键再继续绘制clc;closeal... [详细]
赞
踩
- 在机器学习领域中,支持向量机(SVM)是一种常用的分类算法。然而,传统的SVM在处理大规模数据集时存在一些问题,比如计算复杂度高和对参数的选择敏感等。为了解决这些问题,研究人员提出了最小二乘支持向量机(LSSVM)算法,并结合蛇群算法进行优... [详细]
赞
踩
- 关于lssvr的python实现(这里写自定义目录标题)#lssvr的python实现搜索了一下其他的博客发现代码确实可用,由于个人原因,没有搞清楚如何引入测试集,我认为上述博客中只给出了训练误差的计算方式,当按照同训练集一样的方法引入测试... [详细]
赞
踩
- 时序预测|MATLAB实现LSTM-SVR(长短期记忆神经网络-支持向量机)时间序列预测_lssvrmatlablssvrmatlab时序预测|MATLAB实现LSTM-SVR(长短期记忆神经网络-支持向量机)时间序列预测目录时序预测|MA... [详细]
赞
踩
- matlab实现lstm_matlab实现lstmmatlab实现lstm要在MATLAB中实现LSTM(长短期记忆网络),你可以使用MATLAB中的DeepLearningToolbox。以下是一个简单的例子,演示如何在MATLAB中创建... [详细]
赞
踩
- 时序预测|Matlab实现基于SVR支持向量机回归的电力负荷预测模型_svrmatlabsvrmatlab文章目录预测结果基本介绍程序设计参考资料预测结果基本介绍时序预测|Matlab实现基于SVR支持向量机回归的电力负荷预测模型支持向量机... [详细]
赞
踩
- 时间序列预测|Matlab基于粒子群算法优化最小二乘支持向量机(PSO-LSSVM)的时间序列预测_lssvrmatlablssvrmatlab文章目录效果一览文章概述部分源码参考资料效果一览文章概述时间序列预测|Matlab基于粒子群算法... [详细]
赞
踩
- 本文介绍了多目标规划的数学模型,以及如何使用MATLAB解决多目标规划问题。_多目标规划模型matlab代码多目标规划模型matlab代码✅作者简介:人工智能专业本科在读,喜欢计算机与编程,写博客记录自己的学习历程。... [详细]
赞
踩
- MATLABR2017b中推出的优化工具箱提供了一系列的优化算法,可以用来求解优化问题。本文介绍了如何使用MATLAB自定义优化模型。_matlab优化模型matlab优化模型✅作者简介:人工智能专业本科在读,喜欢计算机与编程,写博客记录自... [详细]
赞
踩
- 求解目标规划的序贯算法clc,clear;x=optimvar('x',2,'LowerBound',0);dp=optimvar('dp',4,'LowerBound',0);dm=optimvar('dm',4,'LowerBound'... [详细]
赞
踩
- 文章目录例子不同算法(lingo)不同算法(Matlab)例子我们由上可以得到线性规划式子:要如何解呢?不同算法(lingo)可以使用lingo软件:结果为14,x1为4,x2为2。然而,mac上没有lingo软件,用Matlab行不行?可... [详细]
赞
踩
- 求解整数规划用@gin()函数求解0-1规划用@bin()函数我认为求解线性规划和整数规划可以用lingo软件,非线性规划还是建议使用matlab求解。_lingo代码lingo代码注意点1、Lingo默认所有变量不为负数,故应先进行定义域... [详细]
赞
踩